Direct position determination using single moving rotating linear array: Noncoherent and coherent processing

Guizhou WU, Min ZHANG, Chaoxin HE, Fucheng GUO

State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System, National University of Defense Technology, Changsha 410073, China

KEYWORDS Coherent signal processing;Constrained Crame´r-Rao lower bound;Direct position determination;Multiple signal classification;Resolution;Rotating linear array

Abstract To improve the resolution and accuracy of Direct Position Determination (DPD), this paper investigates the problem of positioning multiple emitters directly with a single moving Rotating Linear Array (RLA). Firstly, the geometry of the RLA is formulated and analysed. According to its geometry, the intercepted noncoherent signals in multiple interception intervals are modeled.Correspondingly, the MUltiple SIgnal Classification (MUSIC) based noncoherent DPD approach is proposed. Secondly, the synchronous coherent pulse signals are individually considered and formulated. And the coherent DPD approach which aims for localizing this special type of signal is presented by stacking all array responses at different interception intervals. Besides, we also derive the constrained Crame´r-Rao Lower Bound(CRLB)expression for both noncoherent and coherent DPD with RLA under the constraint that the altitudes of the emitters are known.At last,computer simulations are included to examine the performance of the proposed approach.The results demonstrate that the localization accuracy and resolution of DPD with single moving linear array can be significantly improved by the array rotation. In addition, coherent DPD with RLA further improves the resolution and increases the maximum emitter number that can be localized compared with the noncoherent DPD with RLA.

1. Introduction

Localization of multiple emitters from passive observations received by a single moving observer is a problem that attracts much interest for both civil and defense-oriented applications in the signal processing and underwater acoustics etc.The estimation of emitter position is generally performed by a twostep procedure. These methods estimate the intermediate parameters e.g. Directions of Arrival (DOA)1,2, Time of Arrival(TOA)3,Time Difference of Arrival(TDOA)and Frequency Difference of Arravial (FDOA)4,5etc in the first step,and then determine the emitter position using the previously estimated parameters in the second step6-8. Nevertheless, the two-step methods are not guaranteed to yield optimal location results since they ignore the constraint that all measurements must correspond to the same location9.To avoid this problem,a novel localization conception known as Direct Position Determination(DPD)was presented in Ref.10.This work also reported that the accuracy of DPD is superior to the two-step method especially at low Signal to Noise Ratio (SNR).

In the recent years, multiple DPD algorithms have been presented such as in Refs.11-17. In these publications, DPD approaches can be deemed as searching for the emitter position that best matches all the received data.This process is achieved by using the raw received signals from all the sensors together and ending with a localization objective function only related to the emitter position. Therefore, emitter position can be extracted in a single step in DPD. Besides, the DPD approaches also inherently avoid associating estimated parameters with there relevant sources.However,the cost is the computational complexity since raw samples are processed in DPD instead of intermediate parameters in two step methods.

It is worth mentioning that the problem of high accuracy and resolution localization for multiple emitters is crucial and intractable in various practical circumstances, which also attracts much interest in the field of DPD. The existing researches18-22mainly focus on modifying the spectral methods to deal with this problem. Therein, MUltiple SIgnal Classification (MUSIC) and Minimum Variance Distortion Response(MVDR)are reported to be superior methods in resolution and computation when combined with DPD.MUSIC23is a widely used spectral method which makes use of the subspaces of the measurements covariance matrix. The MUSIC based DPD approach18was firstly presented to deal with multiple targets localization cases using multiple static receivers. Recently, with a single moving uniform circle array,a direct location estimator19based on a MUSIC-type objective function is reported which can achieve higher resolution than the traditional Bearings-only Localization (BOL) (e.g.24). On the other hand, the well known spectral method MVDR25which was originally proposed for frequency-wavenumber power spectral density analysis as a high resolution method was also considered to be combined with DPD in Refs.21,22.It is reported that this method achieves superior localization resolution for weak sources with respect to the Maximum Likelihood (ML) based localization methods and circumvents the problem of estimating the number of the emitters. However, the MVDR estimator is asymptotically biased when the intercepted signal is a mixture if signals from several emitters as remarked in Ref.26. The aforementionded approaches have achieved great results in the localization accuracy and resolution of DPD for multiple emitters scenario. However, these works mainly consider the problem in terms of the algorithms to build different objective functions and are subject to that the maximum emitter number should be less than the array element number as spectral methods.

In despite of these improved algorithms, we take novel Rotating Linear Array (RLA) into consideration. Such a time-varying array system is a novel framework which is used to estimate the signal parameters or DOA by exploiting multiple measurements collected at different time instants and associated with different array geometries27,28. The major superiority of the time-varying array system is reduced receiver hardware, which may further reduce the cost, weight and volume.Another advantage is the possibility for precise and high resolution estimation by using the data associated with different array geometries. Besides, the emitter number that can be localized by the time-varying array can be larger than the array element number. In the recent works, the switched-element29and the rotated-element30are the two most ordinarily elaborated geometries.At each time instant,the former selects a different subset of the elements in all given elements to form a different channel by a multiplexer,whereas the latter forms different channel geometries by a rotating mechanism.Compared with the switched-element way, rotated-element system is a more economic way which requires fewer array elements. To limit the scope in this paper, we shall consider a specific rotated-element system i.e. RLA since its simpleness and representativeness.

Therefore,the utilization of RLA in DPD is justified in two aspects. First, this combination may improve the resolution and accuracy of DPD because of the multiple array geometries formed at different time instants. Note that this improvement has not been available in the previous DPD publications which focused on modifying the estimation algorithms. Secondly,DPD with single moving RLA does not require more array elements compared with DPD using general Linear Array (LA),which makes it attractive in application.

Motivated by the above facts, this paper focuses on the DPD with a single moving RLA. The framework follows a similar guideline of traditional DPD approach, but the array geometries, the intercepted signal model, the signal process method, and the obtained results are quite different from previous DPD-related work. Those differences form the major contributions of this paper,which can be concluded as follows.

(1) For the first time, the DPD with a RLA, denoted as RLA-DPD, is proposed in this paper via analyzing the structure of the RLA and formulating the objective function of DPD etc. Note that the derivation and analysis in this paper do not place a restriction on the arrangement of the array element. Thus, nonuniform linear arrays e.g.nested array31and coprime array32are also compatible with RLA-DPD.

(2) The model of noncoherent signals intercepted by the RLA is formulated,then the noncoherent type DPD is presented. For completeness, the intercepted synchronous coherent pulse train signal which can be processed coherently is also considered. Accordingly, coherent type DPD is presented. The MUSIC method is adopted to formulate the objective functions since it is straightforward and compatible with the RLA system. It is noted that the performance of MUSIC based approach is critically dependent on the estimation accuracy of emitter number. In this paper, a simple and efficient nonparametric method33for estimating the number of signals without eigendecomposition is used, in which the additive noise can be defused and signal detection capability is improved. In all simulations involved throughout this paper, no emitter number was miscalculated by this method.

(3) The constrained Crame´r-Rao Lower Bound(CRLB)for noncoherent type DPD and coherent type DPD is derived and analyzed under the constraint that the altitudes of the emitters are known. Note that the constrained CRLB,which is a more exact criterion of localization accuracy,evaluates the effect of the deterministic prior knowledge and results in a lower bound than the unconstrained CRLB.

(4) The performance of noncoherent type and coherent type RLA-DPD is analysed,respectively.The accuracy,resolution and the maximum emitter number that can be localized are adopted as the major criteria of the RLA-DPD performance.

The rest of this paper is organised as follows. Section 2 introduces the structure of the RLA, formulates the signal models of noncoherent and synchronous coherent emitters intercepted by a single moving RLA.Section 3 derives the constrained CRLB for both noncoherent and coherent RLADPD.In Section 4,we present the MUSIC type DPD objective function. Subsequently, Section 5 provides the numerical simulations where the performance of RLA-DPD is analysed in detail. The discussion and conclusion are made in Sections 6 and 7, respectively.

2. Problem formulation

This section introduces the structure of the RLA system and formulates the signal model intercepted by the RLA in a 3-D space. For completeness, the models of nonherent signal and synchronous coherent pulse train signal are both considered.

Here,we would like to first explain the motivation for individually studying the synchronous coherent pulse train signal model besides the completeness.It is well-known that coherent processing of all sensor outputs leads to the optimal solution of localization problem. For DPD using multiple arrays34,the coherent processing method stacks the array responses of all arrays during single interception interval to obtain the improvement of performance. However, coherent type DPD using single array requires identical signal envelope at different interception intervals to pile up the corresponding array responses, which is different from the multiple arrays ones.Fortunately, the synchronous coherent pulse train which is classified as Class 2 Case B coherent signal in Ref.35can satisfy the expectation of the signal envelope in coherent type DPD using single RLA.It will be formulated and analyzed in detail in the following. Note that other coherent signal (eg. asynchronous coherent pulse train35) cannot be processed coherently by the RLA system, which should be deemed as noncoherent signal in the proposed approach of this paper.

2.1. Structure of RLA

Consider a LA composed of M elements mounted on a moving platform. For simplicity, we hypothesis that the LA rotates anticlockwise with a uniform angular speed ω around its center in the plane that parallel to the xy coordinate plane.

The structure of RLA is presented in Fig.1.During a rotating period T, suppose that the RLA intercepts N batches of signals at the rotating angle θnwhere n=1，2，···，N,and samples K snapshots during each signal batch. Denote the time duration of each signal batch as interception interval Tb, then Tb=KTswhere Tsdenotes the sample interval. Note that the parameter zn，kin Fig. 1 denotes the intercepted signals which will be described in the following subsection. For the sake of simplicity, we further assume that the geometry of the RLA is stationary during each interception interval.This hypothesis is reasonable because the interception interval can be a very short time (eg. a pulse width)and the angular speed ω is ordinarily slow constrained by the stability of the system (eg.ω=2πrad/s).Then the positions of the array elements during the n-th interception interval relative to the reference element can be formulated in the following form

where d1denotes the positions of the array elements relative to the reference element at the initial time of the first interception interval, Θ（θn） stands for the rotation matrix with respect to θn, and tnis the initial time of the n-th interception interval.According to the principle of geometry and the assumptions above, d1and Θ （θn） can be calculated as

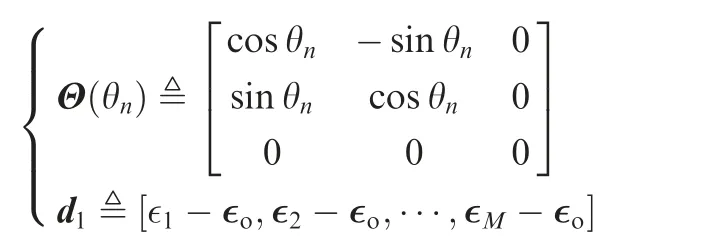
where ∈mand ∈odenote the positions of the m-th element and the reference element at the initial time, respectively.

This subsection has formulated the structure of the RLA.We mention that dnvaries during a rotating period T with respect to different rotated angle θn.Thus,there are N relative positions formed during a rotating period T for each array element except the reference one. However, the relative positions of every array element keep unaltered for the conventional LA system.

2.2. Noncoherent signal model

3. Constrained CRLB of RLA-DPD

It is well known that the CRLB provides a low bound on the covariance of any unbiased estimator. The estimator can be called efficient if it attains the CRLB. Ref.16has given a expression of the CRLB of DPD with single moving circular array. Nevertheless, this work does not evaluate the effect of the deterministic prior knowledge that the altitudes of the emitters are assumed known and,to a certain extent,is incomplete. Generally, the CRLB for a constrained parameter estimation problem is desired to be derived since constraints should result in improved estimates with lower CRLB. For explicit CRLB analysis, we derive the constrained CRLB expression for noncoherent RLA-DPD and coherent RLADPD respectively. Inspired by Refs.5,39, the basic idea can be divided into two steps.First,the original unconstrained CRLB is presented. Then, a nonnegative definite correction matrix with respect to the constrains is defined and calculated.By subtracting it from the unconstrained CRLB, the constrained CRLB can be finally obtained.

3.1. Constrained CRLB of coherent RLA-DPD

Here, the constrained CRLB of coherent RLA-DPD is presented as a benchmark to examine the performance of the proposed method. The derivation is divided into two steps as described above.

3.1.1. Step 1

To derive the unconstrained CRLB of coherent RLA-DPD,we begin by defining a vector ξ of all the real-valued unknown parameters including the emitter locations and the real-part and the imaginary-part of the synchronous coherent pulse signal xk, namely

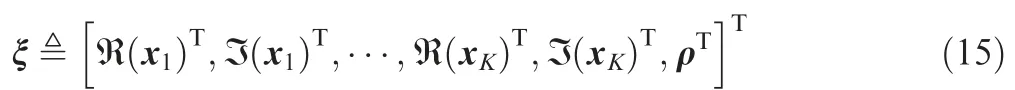
where R（xk） and I （xk） stand for the real and imaginary part of the vector xk. Note that the CRLB can be given by the inverse of the Fisher Information Matrix (FIM) which can be calculated by

with

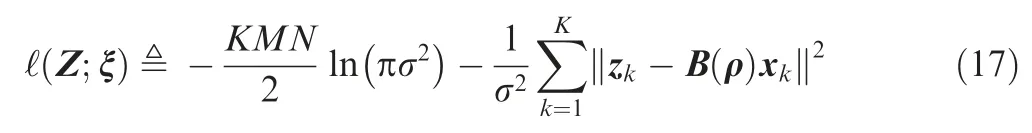
denotes the log-likelihood function where σ2is the variance of the noise. Then, the unconstrained CRLB for the estimation of ρ can be obtained by the calculations which are similar to Ref.40

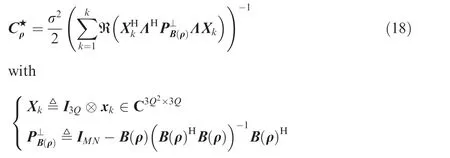
where ⊗denotes the Kronecker product, the superscript ★stands for coherent processing, （·）Hstands for conjugate transpose, I3Qand IMNare 3Q×3Q and MN×MN identity matrixes. Besides, the Jacobi matrix

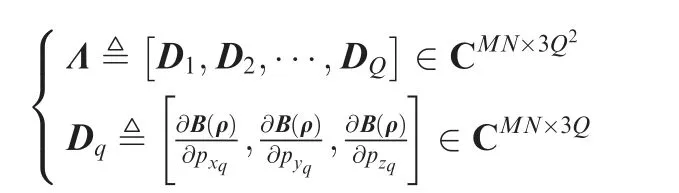
We first derive

where dn，mdenotes the position of the m-th array element during the n-th interception interval relative to the reference element, which can be calculated by

where e1≜［1 ，0，0］T. Similar to Eq. (19),andcan be simply derived. Note that the major difference is

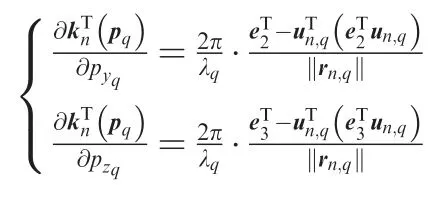
where e2≜0，1，0［ ］T，e3≜0，0，1［ ］T. Finally,can be evaluated by Eqs. (18)-(23).lated with each other.The major distinction between the noncoherent signal and the synchronous coherent pulse signal simulated in this section is that the codes of each pulse from the same emitter are also selected at random for noncoherent signal. However, each synchronous coherent pulse from the same emitter has the identical baseband envelope. For simplicity, suppose that no multipath nor intermittent emission exist and all simulated signals have the same power.

(2) The RLA is equipped on a observer which moves from［- 50，0，200］m to ［5 0，0，200］m straightly. During a rotation period, there are N =8 interception intervals and each interval has K =50 snapshots sampled at Fs=1 MHz. In this case, we assume that each interval samples a complete pulse i.e. K/Fs===···==50 μs from every emitter.

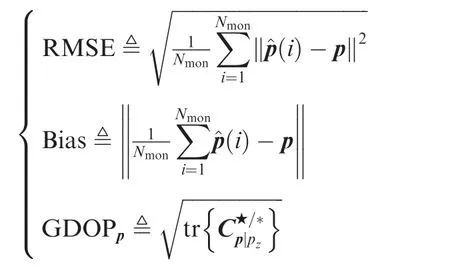
(3) The localization Root Mean Square Error (RMSE),bias and the Geometrical Dilution of Precision(GDOP)are adopted as the criteria of localization accuracy,which are defined by denotes the trace of the matrix C，is the estimated position

where Nmonstands for the number of Monte Carlo trials,tr ｛C ｝at the i-th trial,can be calculated by Eqs.(29)and(34)for coherent RLA-DPD and noncoherent RLA-DPD respectively.To obtain statistical results, Nmonis set to be 100.In this subsection, the localization accuracy of noncoherent RLA-DPD,LA-DPD, RLA-AOA and LA-AOA are compared and analyzed. The trajectory projections of RLA and LA onto the xy plane during the total interval can be found in Fig.2.Note that the geometry of the LA without rotating is constrained to be parallel to the y axis during the total interval.

5.1. Comparison of localization accuracy

In a feasible solution area of 400 m×400 m, the GDOPs of RLA-DPD and LA-DPD are presented in Fig. 3 at SNR=20 dB respectively. Besides, the trajectory projections of the observer onto the xy plane are also marked by triangles.Note that 2-step traditional methods i.e. RLA-AOA or LA-AOA have identical GDOP with DPD19, which will not be repeated in this subsection. It is observed that the localization accuracy sharply deteriorates in the direction of the trajectory i.e. x axis for LA-DPD. This is mainly because that the array response an（p ） of the LA from this direction remains constant at different interception interval i.e.a1（p ）=a2（p ）=···=aN（p ） which results in the directional ambiguity.The inference can be simply verified by noting that dnand kn（p ） in Eq. (3) are unaltered during the total interval for the LA-DPD. On the other hand, the GDOP of RLA is similar to that of the circular array which is superior and unambiguous compared with LA in the entire interesting area.This improvement is resulted from the varying geometry of the RLA.

Next, the localization RMSE of single emitter located at［1 00，100，0］m is examined and compared with the constrained and unconstrained CRLB for both RLA-DPD and LA-DPD.The results are shown in Fig.4.The simulation results indicate that the localization accuracy of LA can be improved by the rotation of the baseline which is consistent with the results given in Fig. 3. Similar with the results in Refs.14,15, the DPD methods including RLA-DPD and LA-DPD have superior localization accuracy compared with 2-step method at low SNR level. Moreover, the RMSE of RLA and LA both can break through the unconstrained CRLB and attain the constrained CRLB at moderate SNR since the MUSIC estimator is a large sample realization of the ML estimator.As expected,the constrained CRLB is smaller than the unconstrained CRLB,which is consistent with the theoretical analyses in Section 3. Besides, the proportionality of the constrained CRLB given in Eq.(18)with the emitter position and the SNR is also verified by the results.

5.2. Comparison of resolution

In this subsection, we only focus on the geometry of the array which inherently results in the improvement of resolution.Despite the various high resolution methods e.g. MVDR, we examine the resolution by illustrating the mean objective functions of noncoherent RLA-DPD and noncoherent LA-DPD utilizing the identical MUSIC method via Nmon=100 Monte Carlo trials. In particular, four closely spaced emitters are considered. The projection of the observer trajectory and the emitter positions are shown in Fig. 5.

To clearly examine the resolution, the contours of the normalized objective functions of RLA-DPD and LA-DPD at high SNR (20 dB) are presented with the identical contour levels i.e. v= ［0.01，0.05，0.2，0.5，0.7］. In an area of 30 m×30 m centered around the emitters,the results are given in Fig. 6 where the real emitter positions are also marked.Therein, the DPD objective function of LA presents only two peaks at contour level v=0.7 since its resolution deteriorates in the y axis direction. On the other hand, the objective function of RLA-DPD shows three peaks around the real emitter positions at contour level v=0.7 and the peaks are more significant compared with that of LA-DPD.

Fig. 2 Trajectory projections of RLA and LA onto xy plane.

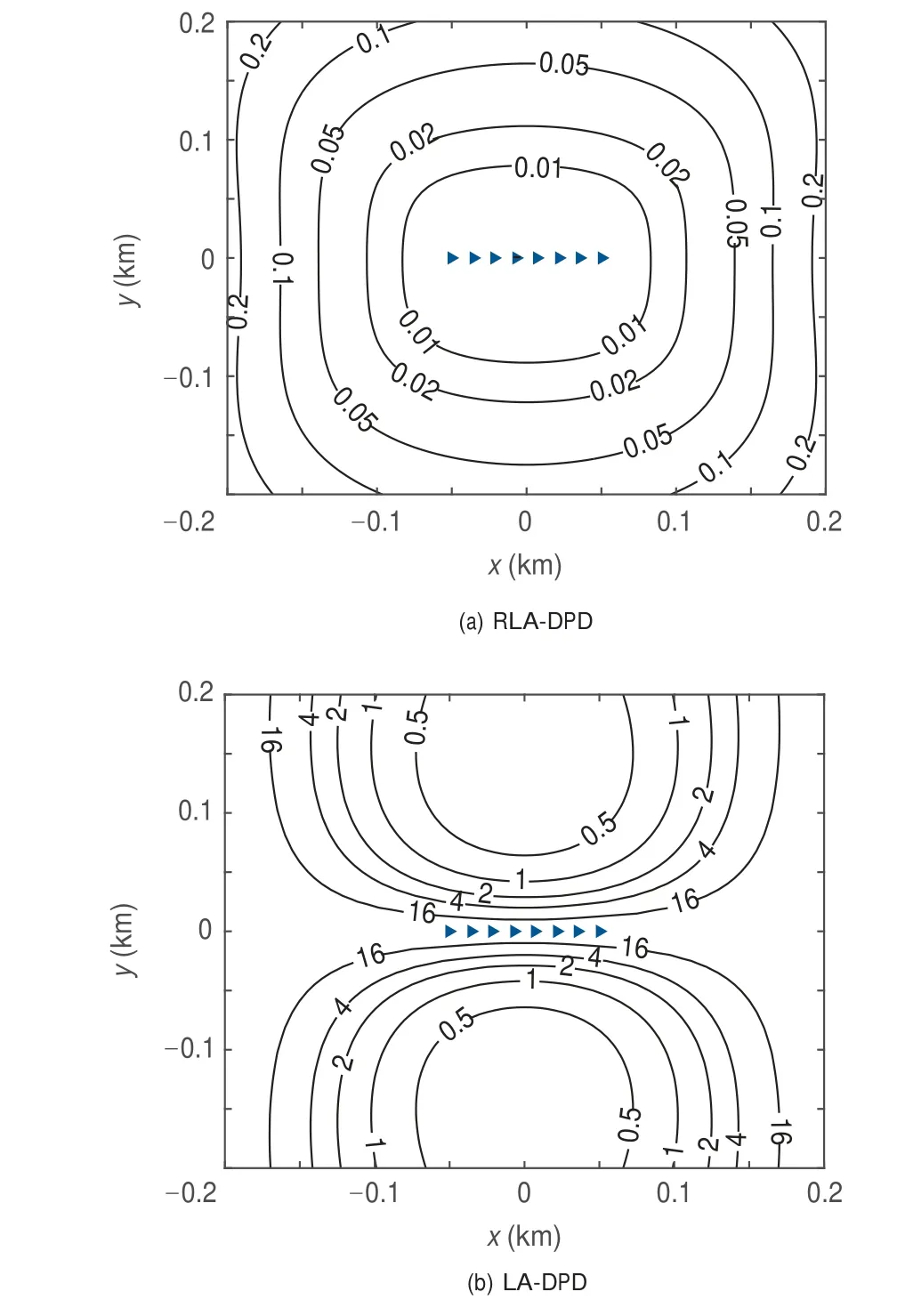
Fig. 3 GDOPs of RLA-DPD and LA-DPD.

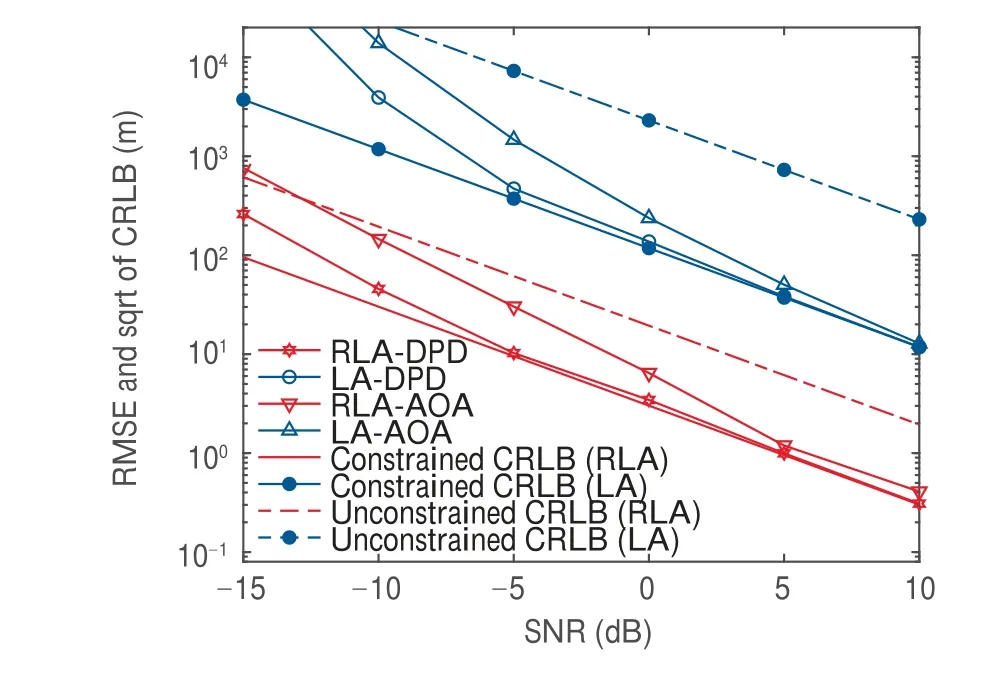
Fig. 4 RMSE and sqrt of CRLB vs. SNR for RLA-DPD,LA-DPD, RLA-AOA and LA-AOA.

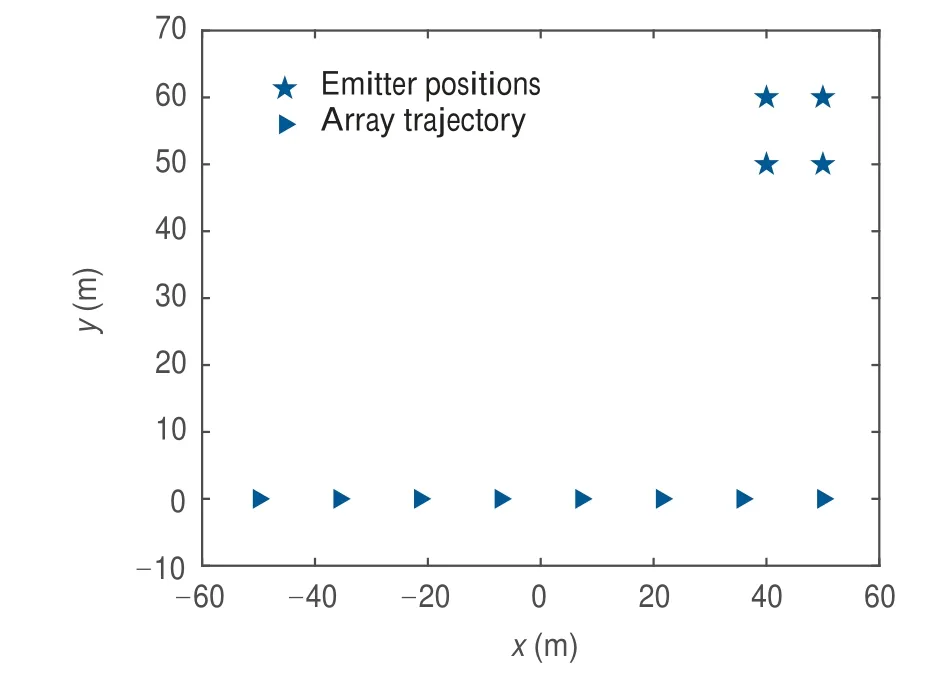
Fig. 5 Projections of observer trajectory and emitter positions.

Remark: Since the identical estimator (MUSIC method) is used, it is justified to infer that the resolution of LA-DPD is improved by the array rotation. Note that the merged peak may split into two peaks at a higher contour level e.g.v=0.75. Even so, the merged peak at contour level v=0.7 is still inapparent which will be easily buried in the noise at moderate SNR. The problem of resolution for the same scene will be further studied in the following subsection where different results will be presented.

5.3. Coherent RLA-DPD study

In this section, we focus on the coherent RLA-DPD which is introduced in Section 4.2.Accordingly,the signals are the synchronous coherent pulse as described above.Besides the examination of localization accuracy and resolution, we also verify the ability of coherent RLA-DPD to estimate more emitter positions i.e. Q>M.

5.3.1. Localization accuracy

Giving the same conditions as described in Section 5.1, we illustrate the GDOP of the coherent RLA-DPD. Surprisingly,the result is exactly identical with the noncoherent RLA-DPD ones as shown in Fig. 3. Namely, the coherent RLA-DPD does not improve the localization accuracy at all. This result is different from the coherent DPD with multiple arrays because their coherent processing methods are absolutely different. Coherent DPD with multiple arrays stacks the array responses of all arrays and accumulates the observations of different interception intervals. However,coherent DPD with single moving sensor can only pile up the array responses of different interception intervals and lack the cumulative step. This is an important result for the DPD with single moving array.

5.3.2. Localization resolution

For the same scene as shown in Fig. 5, we illustrate the mean objective functionof coherent RLA-DPD by Nmon=100 Monte Carlo trials. The contour of the mean normalized objective function with the same contour level v as introduced in Section 5.2 is shown in Fig. 7. We observe that the objective function of coherent RLA-DPD shows four peaks around the real emitter positions at contour level v=0.5.Note that at this contour level, the objective function of noncoherent RLA-DPD as illustrated in Fig. 6 presents only two merged flat peaks. At contour level v=0.7, four sharp peaks can be found in Fig. 7, whereas only three peaks are shown in Fig. 6. This result verifies that the resolution of RLA-DPD can be improved by coherent process, although the accuracy of coherent RLA-DPD is identical with noncoherent RLA-DPD.

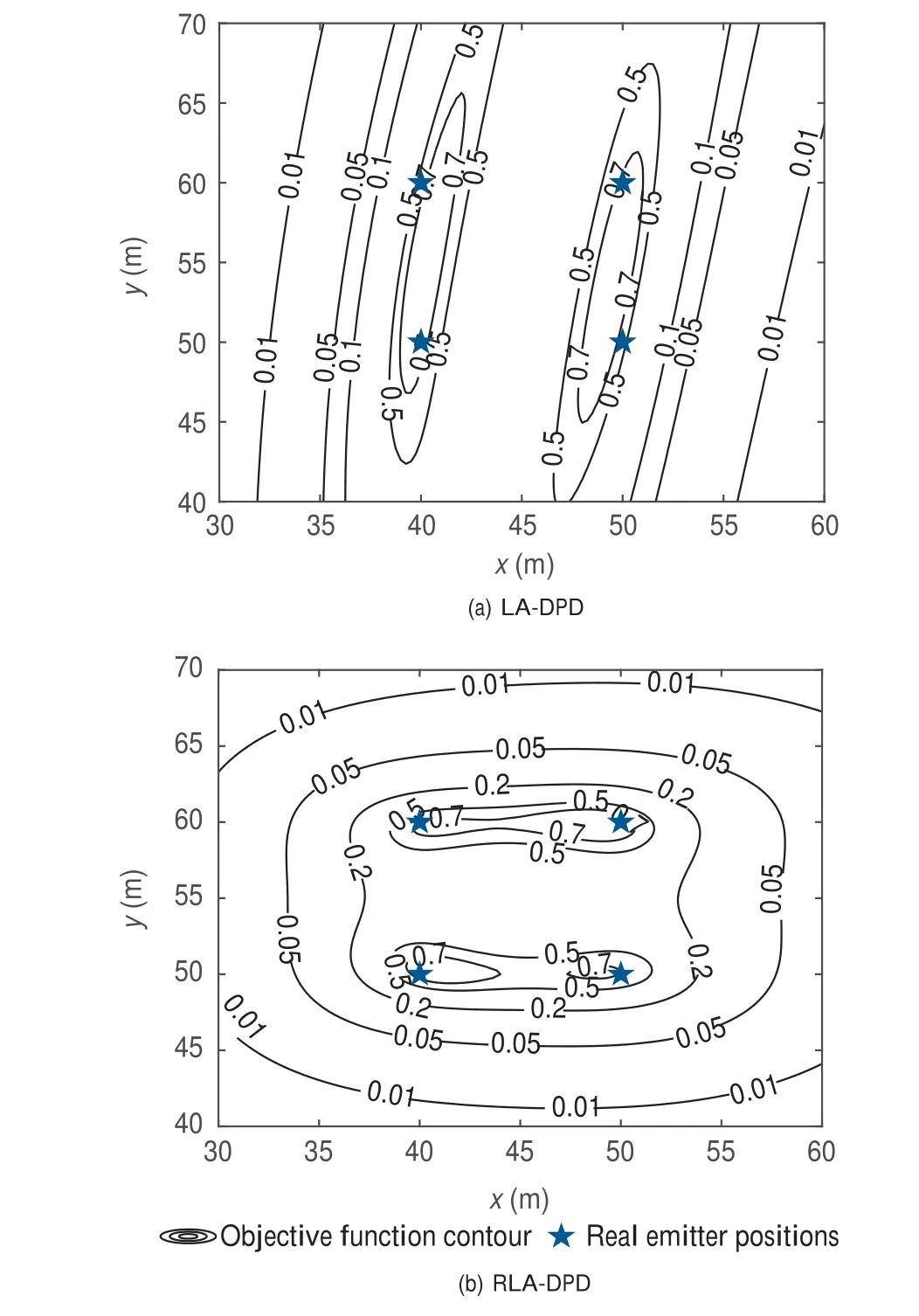
Fig.6 Objective function filled contours of LA-DPD and RLARLA.

Next,a more convincing simulation is performed where the localization RMSE and Bias of the emitter located at 40，50［ ］m, which is denoted as Emitter 1, are examined and analysed. Other emitters have similar results, which will not be introduced for the sake of clarity.Note that the localization bias is considered to assess the interference of other adjacent emitters since it will be large when the estimators can not distinguish the closely spaced emitters. The results are shown in Fig. 8. Therein, the RMSE of noncoherent LA-DPD is approximately independent with SNR and cannot attain the CRLB due to the Bias that resulted from the interference of other adjacent emitters. This inference can be verified by the result of the bias of noncoherent LA-DPD, which is always a large value at different SNR level. On the other hand, the RMSE of noncoherent and coherent RLA-DPD both can reach CRLB. And the biases of noncoherent and coherent RLA-DPD reduce as the increase of the SNR,which indicates that the their resolution are improved. In addition, an important result is that coherent RLA-DPD holds a superior resolution over noncoherent RLA-DPD when the SNR ＜25 dB,which is consistent with the levels and the tendencies of their biases.

5.3.3. Emitter number examination

Note that by the coherent processing method, up to MN-1 emitters can be localized by the single moving RLA as analysed in Section 4.2. To verify it, we use LA with M=2 elements instead of the LA introduced above in the RLA system. Thus the maximum emitter number that can be localized should be MN-1=15.

In this subsection,Q=12 emitters of synchronous coherent pulse are considered as example whose positions are listed in Table 1.The SNR is set to be 60 dB.Then,the estimated emitter positions by the coherent RLA-DPD is illustrated in Fig.9 where the real emitter positions are also remarked. It is observed that the estimated emitter positions are shown around the real emitter positions, viz., all these emitters can be localized by the RLA consists of M=2 elements. Meanwhile, the localization RMSE and Bias are also shown in Table 1.

6. Discussions

We will discuss whether noncoherent and coherent RLA-DPD has a good performance in practice compared with noncoherent LA-DPD from two aspects. One is the improved effect including the localization accuracy, resolution and maximum emitter number that can be localized,the other is the cost that can not be avoided e.g.the computational complexity,the system requirements, the bias that may be introduced and the applicable signal types etc.

For noncoherent LA-DPA mentioned above, the performance in localization accuracy and resolution is poor as showed in Section 6. The computational complexity of it may be the major advantage. If exhaustive search is used to solve the optimization problem,this framework approximately costs NM3Ngmultiplications where Ngstands for the number of grid in the exhaustive search. Besides, the applicable signal type is not limited,rotating mechanism is not required,and the measurement of rotated angle θ is avoided.

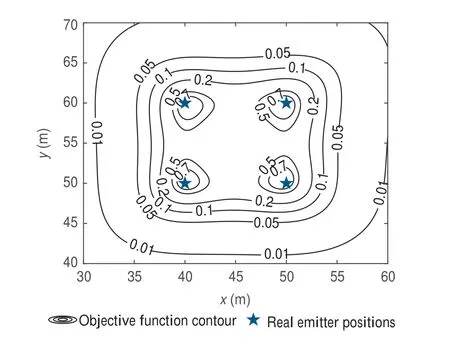
Fig. 7 Objective function filled contour of coherent RLA-DPD.

Fig. 8 RMSE, Bias and sqrt of constrained CRLB vs. SNR(Emitter 1).

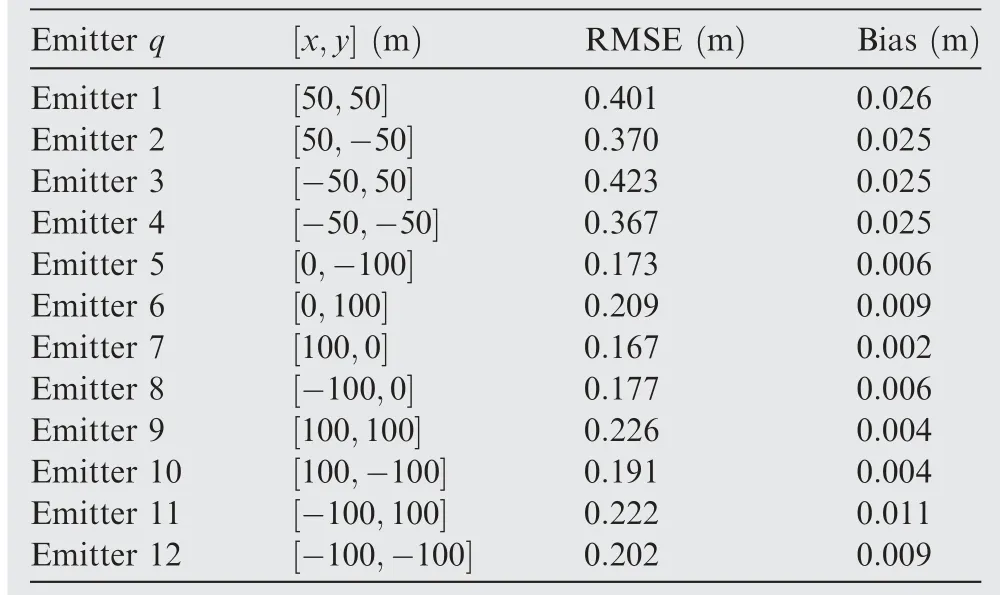
Table 1 Positions and localization results of emitters.

For noncoherent RLA-DPD, the performance in localization accuracy and resolution is improved significantly by the rotation of the array baseline as shown in Sections 5.1 and 5.2 respectively.Its GDOP is even similar to the circular array.And the noncoherent RLA-DPD does not require more computation than that of other LA-DPD except the additional calibration of dn（n=1，2，···，N）. The total number of multiplications required in this framework can be approximately given by NM3Ng+9M which is almost identical with LA-DPD. Meanwhile, all narrow-band emitters can be localized by the noncoherent RLA-DPD although only radar pulse signals are considered in the simulations. The major cost would be the rotating mechanism and the measurement bias of rotated angle θn. As results, the rotating mechanism will increase the weight and cost of the whole RLA-DPD system,

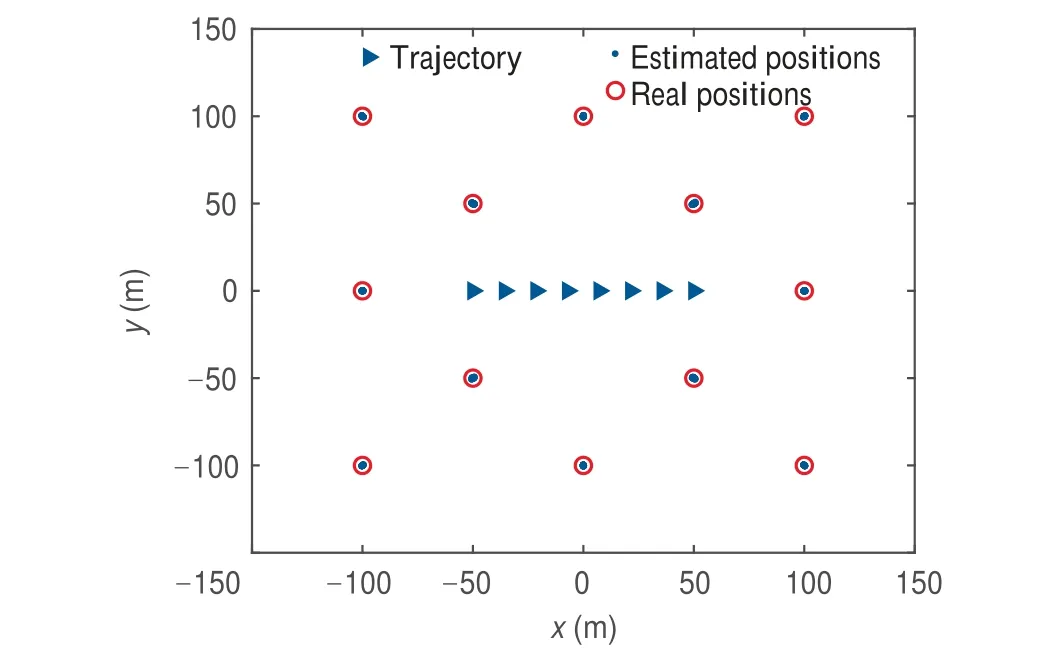
Fig. 9 Objective function contour of coherent RLA-DPD for Q=12 emitters.

while the bias will result in the localization error. Bias compensation of θnshould be another interesting problem.We skip it over due to space limitation and leave it for future research.

For coherent RLA-DPD, the localization resolution is improved and the maximum emitter number that can be localized is also increased from M-1 to MN-1 compared with noncoherent RLA-DPD when the RLA is a rotating ULA. But its accuracy is identical with noncoherent RLADPD. Note that coherent RLA-DPD can only process the synchronous coherent pulse signals and have to decompose the MN×MN matrix ^R (see Eq. (38)), whereas noncoherent RLA-DPD just requires to decompose the M×M matrix ^Rn(see Eq. (36)). Considering the dimensional explosion of the matrix, the total number of multiplications required in this framework becomes N3M3Ng+9M. Besides, other cost of coherent RLA-DPD is the same to that of the noncoherent RLA-DPD. The restriction on the applicatory signal type will significantly limit its practical application. Table 2 concludes these discussions for all considered DPD with a ULA-DPD.

Table 2 Improvement and cost of noncoherent and coherent RLA-DPD.

7. Conclusions

Now we conclude this paper.We focus on the geometry of the single moving LA used in DPD and propose a novel framework system denoted as RLA-DPD. Coherent RLA-DPD for synchronous coherent pulse signal and noncoherent RLA-DPD for all narrow-band signal are investigated and analyzed respectively. Through the simulation and analysis,the following results are reported:

(1) RLA-DPD can significantly improve the localization accuracy and resolution by the rotation of the baseline compared with LA-DPD.

(2) For noncoherent RLA-DPD,the performance improvement appears just at a small cost of rotating mechanism.

(3) Coherent RLA-DPD has the identical localization accuracy with noncoherent RLA-DPD. However, it can further improve the resolution and increase the maximum emitter number that can be localized.

(4) Coherent RLA-DPD can only process the synchronous coherent pulse signal and its computational complexity are also increased.

Besides, we also recommend DPD with multiple RLAs or RLA-DPD utilizing other efficient methods e.g.ML estimator to obtain better performance improvements. The relevant research will be provided in the near future.

Acknowledgments

This research was funded by the National Defence Science and Technology Project Fund of China (No. 3101140), the Shanghai Aerospace Science and Technology Innovation Fund of China (No. SAST2015028), and the Equipment Prophecy Fund of China (No. 9140A21040115KG010 01).