Switching control of morphing aircraft based on Q-learning
Ligang GONG, Qing WANG, Changhua HU, Chen LIU
a School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China
b Science and Technology on Space Intelligent Control Laboratory, Beijing Institute of Control Engineering, Beijing 100190, China
c Xi’an Institute of High Technology, Xi’an 710025, China
d School of Aeronautic Science and Engineering, Beihang University, Beijing 100083, China
e Beijing Institute of Electric System Engineering, Beijing 100854, China
KEYWORDS Back-stepping;Command filter;Disturbance observer;Morphing aircraft;Q-learning;Switching control
Abstract This paper investigates a switching control strategy for the altitude motion of a morphing aircraft with variable sweep wings based on Q-learning. The morphing process is regarded as a function of the system states and a related altitude motion model is established.Then,the designed controller is divided into the outer part and inner part, where the outer part is devised by a combination of the back-stepping method and command filter technique so that the‘explosion of complexity’ problem is eliminated. Moreover, the integrator structure of the altitude motion model is exploited to simplify the back-stepping design, and disturbance observers inspired from the idea of extended state observer are devised to obtain estimations of the system disturbances.The control input switches from the outer part to the inner part when the altitude tracking error converges to a small value and linear approximation of the altitude motion model is applied.The inner part is generated by the Q-learning algorithm which learns the optimal command in the presence of unknown system matrices and disturbances. It is proved rigorously that all signals of the closed-loop system stay bounded by the developed control method and controller switching occurs only once.Finally,comparative simulations are conducted to validate improved control performance of the proposed scheme.
1. Introduction
The morphing aircraft possesses changeable aerodynamic configuration to enhance the adaptability to multiple missions,which can achieve optimal flight performance in different flight environments.1-3The change of configuration guarantees the improvement of flight performance and expands the range of aerodynamic characteristics. However, the aircraft becomes a complicated system with large parameter variations including mass distribution and applied aerodynamic forces due to the morphing process.4,5Furthermore, the existence of internal uncertainties and external disturbances makes the control of morphing aircraft a changeling problem, which has attracted considerable attention during the past few decades.
The extant research on morphing aircraft control mainly focuses on the longitudinal dynamics, and related model simplification methods are developed. The Linear Parameter Varying (LPV) system is adopted to facilitate the modeling of a folding-wing morphing aircraft in Ref.6and simulation of the open-loop dynamic responses validates the LPV model.Moreover, for the LPV model established in Ref.6, a multiloop controller is designed in Ref.7via a combination of linear quadratic optimal control and gain self-scheduled H∞robust control. A variable-sweep morphing aircraft is studied in Ref.8and the related LPV model is obtained by developing a tensor product modeling approach. An LPV controller is then designed with the LPV model to guarantee stability of the closed-loop system. The trajectory-attitude separation control of a gull-wing morphing aircraft is achieved in Ref.9by the LPV method and the control command is generated by both state feedforward and feedback. With wing sweep angle and wingspan treated as scheduling parameters, the LPV model is also presented in Ref.10and Ref.11for a kind of largescale morphing aircraft, where sliding mode controllers with finite time convergence and L2gain performance are proposed,respectively. Apart from the framework of LPV system,switched systems are also deployed for modeling of morphing aircraft in recent years.In view of the short-period property of the transition motion, a series of equilibrium points along the wing deformation process is computed in Ref.12and the longitudinal dynamics is regarded as switched linear systems with disturbances, which is handled by devising a robust switching controller. As a generalization of switched linear systems, the switched LPV systems are investigated in Ref.13for deducing the model of a variable-sweep morphing aircraft. Smooth switching controllers are then designed via the scheduling parameter subsets with overlaps. Similar with the switched LPV modeling scheme in Ref.13, the asynchronous switching between the controllers and subsystems is further studied in Ref.14and Ref.15, where non-fragile and finite H∞control problems are separately considered.
Despite the previous efforts on morphing aircraft control,they mainly belong to the linear case with a requirement of Jacobian linearization for simplifying the dynamic model and designing related controllers. It is noteworthy that the nonlinear characteristics of the morphing aircraft dynamics confine further improvement of control performance via these techniques.Meanwhile,several nonlinear control approaches have also been addressed. A nonlinear time-varying model is devised for a telescopic wing morphing in Ref.16with aerodynamic characteristics revealed by wind tunnel tests. Sliding mode method is then adopted to compute the multi-loop control command with consideration of the time-scale separation property.The altitude motion model of a morphing aircraft in the sweeping process is converted into normal form in Ref.17via coordinate transformation, which is steered by a combination of adaptive neural control and a high-order chained differentiator. Adaptive dynamic surface control is proposed in Ref.18with the derivatives of virtual control laws generated by the sliding mode differentiator. In view of unknown parameters and input-output constraints of the model, neural networks are hence employed to obtain the control commands.The adaptive neural control scheme is further investigated in Ref.19to solve the prescribed performance problem, where the constraints on neural networks for approximation of nonlinearities are relaxed by designing a smooth switching function. Besides, there are also a few results on control of morphing aircraft under the framework of switched nonlinear systems. A combination of dynamic surface control technique and fuzzy systems is proposed in Ref.20for the attitude motion model of a variable structure near space vehicle described by switched nonlinear systems. The modeling and control of the longitudinal motion of an air-breathing hypersonic vehicle with variable geometry inlet are studied in Ref.21, where multiple models corresponding to the translating cowl are adopted and the related multi-model switching controller is devised.Although the aforementioned control methodologies for morphing aircraft can manage the variations in mass distribution and related aerodynamic parameters to a certain degree, the morphing process is commonly considered as predefined functions of time and the influence on flight performance is hence neglected. For this reason, this paper will take the morphing process as a function of the system states so that flight performance is enhanced, which is more consistent with the purpose of morphing.Besides,most of the above studies deal with system disturbances via robustness of the designed controller,while the Extended State Observer(ESO)views the system disturbances as an extended state which is estimated by the ESO and then canceled out in real time by the controller.22,23To this end, disturbance observers motivated by the idea of ESO are designed in this paper to achieve disturbance rejection.
On the other hand, the reinforcement learning control approaches have been presented for optimal control problems during the past decade,24-26which constitute supplements of extant methods for further improvement of control performance. As a remarkable strategy of reinforcement learning control techniques,Q-learning scheme is model-free and learns an action-dependent value function (also known as Qfunction) to determine the optimal control action.27,28The Q-learning based control schemes relies on the definition of an appropriate Q-function related to the action adopted. The Q-function satisfies an equation similar with the Bellman equation which can be solved approximately by neural networks for general nonlinear systems,or formulated in quadratic form for linear systems. The optimal control input can be determined once the Q-function is obtained even when the model is unknown, which constitutes the main merit of Q-learning.From theoretical aspect,the Q-learning methodology has been applied to various classes of linear and nonlinear systems.The linear quadratic regulator problem of unknown continuoustime linear systems is addressed in Ref.29, where an online Q-learning algorithm is devised to generate the optimal control input. The Q-learning technique is developed in Ref.30for model-free optimal tracking control of general non-affine nonlinear discrete-time systems with a critic-only implementation structure. An integral reinforcement learning scheme is adopted in Ref.31to implement the Q-learning algorithm which adjusts weights of the actor and critic simultaneously.The output feedback control for the discrete-time linear zero-sum games and linear quadratic regulator problem are addressed in Refs.32and33,respectively.The discounting factor is eliminated to enhance the stability and related excitation noise problem is avoided. A tradeoff between the current and future value of the Q-function is achieved in Ref.34so that the admissible requirement of the initial control policy is circumvented. The related Q-learning algorithm is devised under the framework of off-policy and combined with the experience replay approach to improve the efficiency. An off-policy Qlearning method for affine nonlinear discrete-time systems is devised in Ref.35, where the unbiasedness of the optimal solution is proved rigorously. A quantitative analysis of the Qlearning scheme with function approximation errors is provided in Ref.36. The relationship between the error bound for estimation of the optimal value of Q-function and the function approximation is illustrated via developing a novel operator.
Although there are numerous studies on Q-learning in theory, the references from the aspect of engineering application are relatively few. A random neural Q-learning scheme is developed for an autonomous mobile robot in Ref.37to obtain the collision-free behavior in the presence of unknown environments, where the weights are updated via extreme learning machine with constraints. A multistep policy evaluation technique is combined with the Q-learning approach in Ref.38to generate the optimal controller for the Quanser helicopter without model information. The step-size is tuned adaptively to expedite the convergence rate of the developed algorithm.Nevertheless, there is little research on Q-learning control of morphing aircraft in recent years.Besides,the existing research on Q-learning methodology for nonlinear systems cannot ensure stability of the closed-loop system in the presence of disturbances.A combination of sliding mode technique and reinforcement learning method called adaptive dynamic programming is proposed in Ref.39for tracking control of air-breathing hypersonic vehicles,where the adaptive dynamic programming approach generates a supplementary control action to reduce tracking errors. However, the reinforcement learning algorithm in Ref.39is in discrete-time domain and influence of disturbances is ignored,which makes it less applicable to our problem. Therefore, this study conducts an exploratory investigation via a combination of the modelbased design scheme and the reinforcement learning method.
To summarize, this paper focuses on switching control for the altitude motion of a morphing aircraft with variable sweep wings based on Q-learning, where the morphing process is related to the system states for improvement of flight performance. The switching in our work represents the switching of the controller.Specifically,a switching type controller composed of the outer part and inner part is developed. The control input is first generated by the outer part where the backstepping technique is adopted and combined with command filter technique to eliminate the‘explosion of complexity’problem.Moreover,disturbance observers inspired from the idea of ESO are developed to design the virtual control laws so that disturbance rejection is achieved. The integrator structure of the altitude motion model is employed to simplify the backstepping design. Then, the control input is determined by the inner part when the altitude tracking error converges to a small value and linear approximation of the altitude motion model is thus feasible. For the inner part, the Q-learning approach is devised in the presence of unknown system matrices and disturbances,which can further improve the control performance.All signals of the closed-loop system are proved to be bounded and controller switches from the outer part to inner part only once.Finally,the advantage of the proposed control strategy is demonstrated by comparative simulation studies.
2. Model description
The morphing aircraft considered in this study has variable sweep wings similar with the research in Refs.17,18, which is depicted in Fig. 1.
The altitude motion model of the morphing aircraft can be described by
where h,γ,α and q denote the altitude,flight path angle,angle of attack and pitch angular rate, respectively; V denotes the velocity; m and Iyrepresent the mass and moment of inertia of the aircraft, respectively; g is the gravitational acceleration;T and ZTdenote the thrust and moment arm of the engine,respectively; L, D and MAdenote the lift force, drag force and pitch moment, respectively. FIkz, FIzand MIystand for the inertial forces and moment caused by the morphing process, which are given as
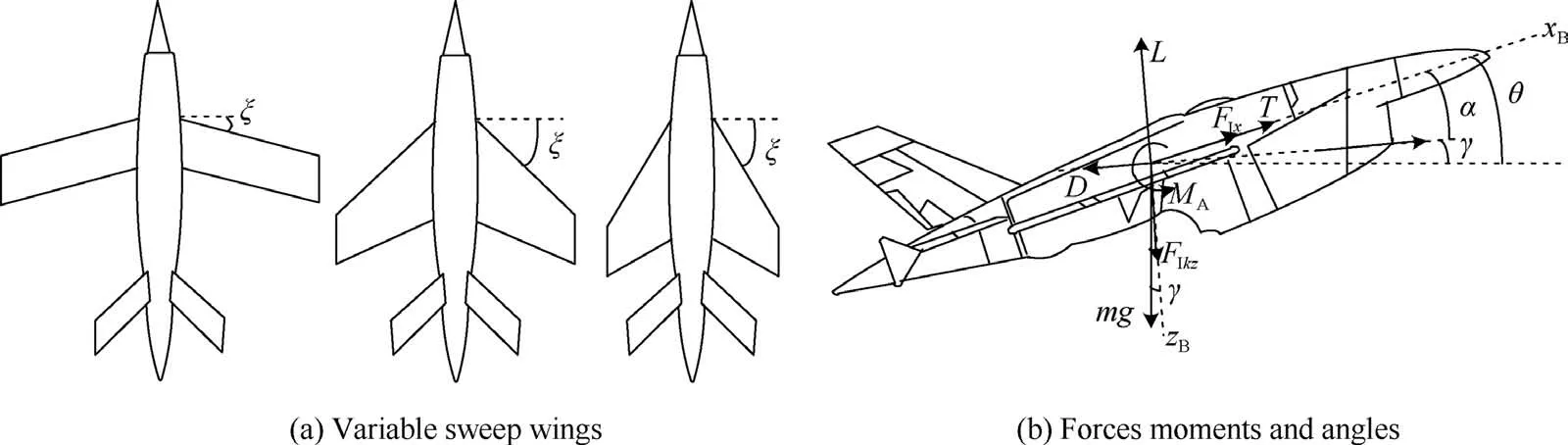
Fig. 1 Schematic diagram of morphing aircraft.
Where m1and m3represent the mass of the wing and fuselage of the aircraft,respectively,r1xand r3xdenote the position of related components in the body frame,=ρhV2/2 is the dynamic pressure, ρhis the air density, ξ is the sweep angle,Sw(ξ)is the wing surface,cA(ξ)denotes the mean aerodynamic chord and δestands for the elevator angle.,,denote the aerodynamic derivatives which can be formulated as polynomial functions of the sweep angle ξ via the computational fluid dynamics technique.The specific expressions will be given in the simulation for completeness and more related definitions are provided in Refs.17,18.
For the altitude motion model given by Eq.(1),we have the following assumptions:
Assumption 1. The sweep angle is a smooth function of h, V and α, i.e., ξ=ξ(h,V,α).
Assumption 2. The flight path angleγ is small, i.e., sinγ ≈γ.
Assumption 3. The velocity V is a constant.
Remark 1. Assumption 1 indicates that ξ is a function of h,Vand α,which can be determined based on the specific requirement of flight performance.1-3Assumption 2 is common and generally adopted in the research on morphing aircraft control.18,19Moreover, we invoke Assumption 3 since the focus of our paper is altitude control and the stability analysis can hence be simplified. Similar assumptions can also be found in Refs.13-15
With Assumptions 1-2,the related dynamics of the altitude reads

We note from Eq. (2) that the aircraft model is nonlinear and disturbances should be considered for controller design.Although the model-based methods including the backstepping technique can ensure stable altitude tracking control,the transient performance is usually neglected and cannot be optimized directly in the design process. To further improve the tracking control performance, this paper conducts an exploratory investigation via a combination of the modelbased design scheme and the reinforcement learning method.The Q-learning scheme is adopted as the reinforcement learning technique in view of its aforementioned merits. However,stability of the closed-loop system is seldom guaranteed in extant research on Q-learning for nonlinear systems due to the existence of disturbances.As a result,a switching type controller is devised in view of the property of the system model,where the Q-learning method is adopted for the local linear model of the aircraft dynamics. The specific controller design process is provided in the next section.
Remark 2. The morphing effect is indeed partially known since the expressions of functions fγ, gγ, fqand gqinclude the terms related to aerodynamics. However, the terms related to inertial forces and moment due to morphing are unknown and regarded as disturbances.The availability of fγ,gγ,fqand gqis exploited for derivation of outer part controller via the command filtered back-stepping technique. Besides, the local linear model is generated by the computation of the value of functions fγ, gγ, fqand gqat the equilibrium point while the further computation of differentiation can be eliminated for the sake of simplicity. Correspondingly, the inner part controller is devised based on an unknown linear model,where the Q-learning method is hence employed in view of its merits of model-free and online learning.
3. Switching controller design
Before the controller is designed, it follows from Eq. (2) that there exist disturbances dγand dqin the dynamics of γ and q,respectively. To guarantee the control performance, we hence first design disturbance observers to generate the estimations of dγand dq, which are compensated for in the controller design procedure. With the devised disturbance observers,the switching controller composed of two parts is then proposed: the outer part and inner part. For the outer part, the command filtered back-stepping method is devised and the integrator structure of the dynamics of θ and q is employed to simplify the controller design. The tracking errors can be guaranteed to enter into a neighborhood of the origin with the outer part controller and local linearization can thus be achieved for the altitude motion model. The controller then switches to the inner part which is developed by the Qlearning approach to further improve the control performance.We note that the inner part can ensure the boundedness of all signals of the linearized system,which will be illustrated in the subsequent analysis.
3.1. Disturbance observer design
Suppose that the nonlinear system is given by

where x, u and d represent the state, control input and disturbance of the system, respectively. f(x) and g(x) are known nonlinear functions. The following assumption is then made to facilitate the convergence analysis of the disturbance observer.
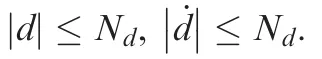
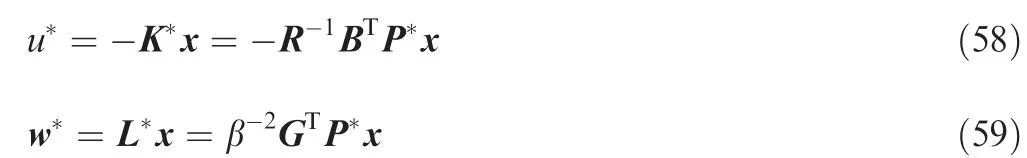




Moreover,the related value function can be represented by S*(x(ts))=xT(ts)P*x(ts) and the Hamiltonian associated with Eqs. (53) and (54) becomes
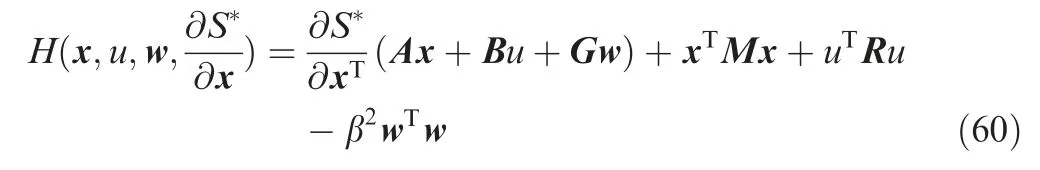
The following Q-function is then introduced by combining the value function with the Hamiltonian:

where U=[xT,u,wT]T, Qxx= P*+M+P*A+ATP*,Qxu=P*B, Qxw=P*G, Qux=BTP*, Quu=R, Quw=0,Qwx=GTP*, Qwu=0, Qww=-β2I. With Eq. (61), the saddle point can also be expressed as u*=-(Quu)-1Quxx,
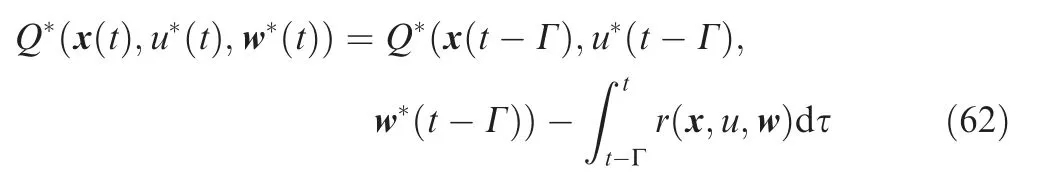
where Γ denotes the user defined time interval. Since the system matrices are unknown, the approximated expressions of the Q-function,control policy and disturbance policy are then adopted to generate the model-free controller. It follows that Q*(x,u*,w*) can be formulated as

where vech(Q-) represents the half-vectorization ofwith the off-diagonal elements multiplied by 2,and(U ⊗U)denotes the Kronecker product which can be expressed as {UiUj},i=1,2,...,9;j=i,i+1,...,9.Let Wc=vech()whose estimated weight is denoted by ^Wc, and we then have the estimation of Q*(x,u,w) described by

Similarly,the approximations of the control policy and disturbance policy can be written as

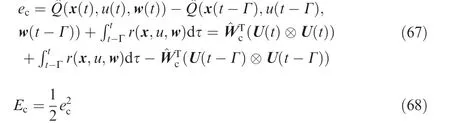
The error functions eau,eawand related object functions Eau,Eawfor training ^Wauand ^Waware defined as
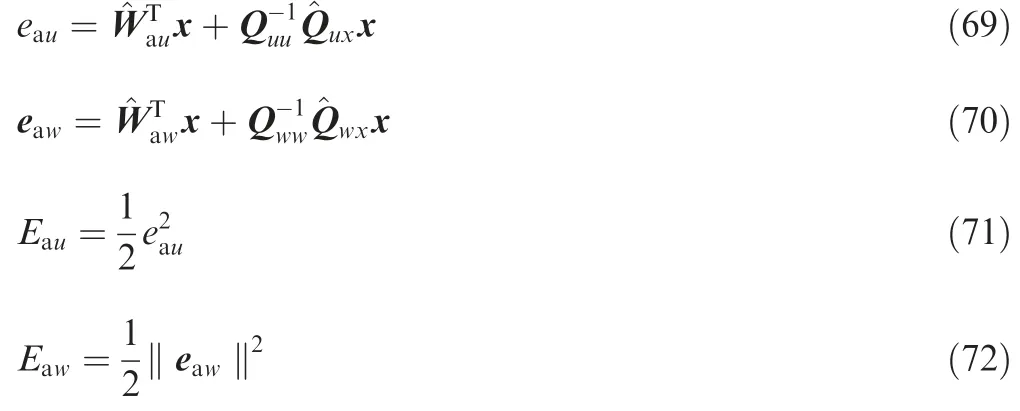
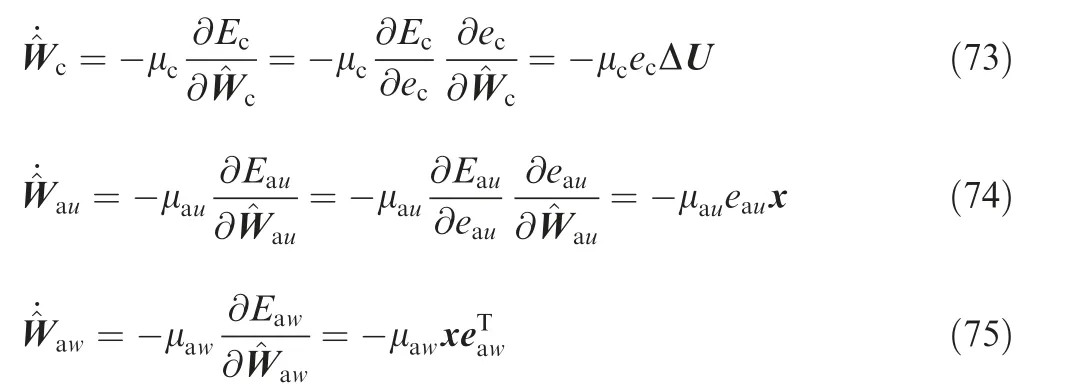
where μc, μauand μaware positive constants which determine the learning rates, ΔU=U(t)⊗U(t)-U(t-Γ)⊗U(t-Γ).The update law for ^Wcis further normalized31to obtain

Theorem 3. Consider the closed-loop system formed of the plant (52), the approximation of the Q-function (64), the control policy(65)and disturbance policy(66)with the update laws given by Eqs.(74)-(76).Suppose that initial values of the closed-loop system are bounded. Then there exist the design parameters M, R, Γ, β, μc, μauand μawsuch that all signals of the closed-loop system with the state composed of x,,,andstay bounded.
Proof. The dynamics of closed-loop system is given by
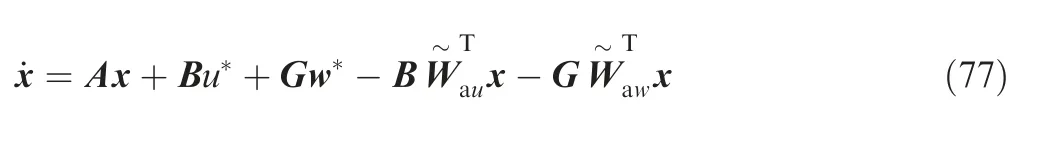
Moreover, the error dynamics of,andcan be written as
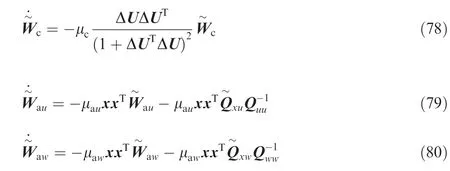

Differentiating Lcwith respect to time yields
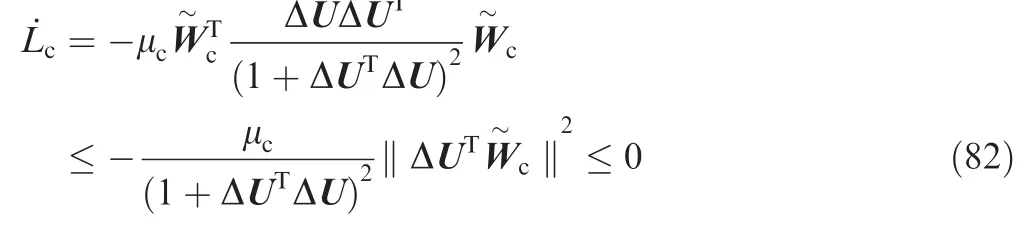
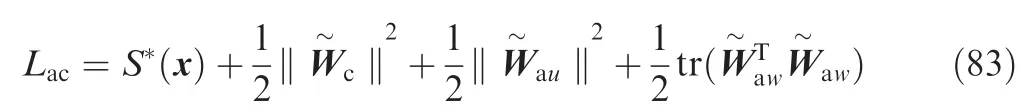
Taking the derivative of Lacalong the trajectories of Eqs.(78-80) implies
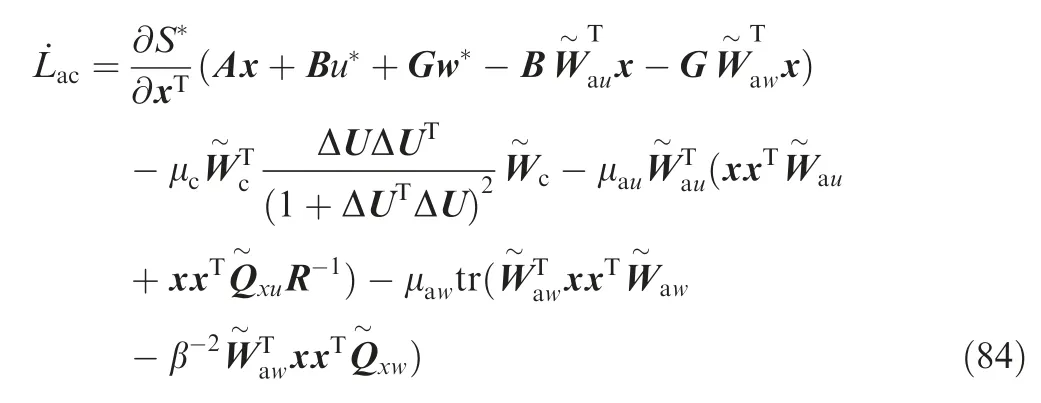
For the first term on the right-hand side of Eq. (84), it follows that
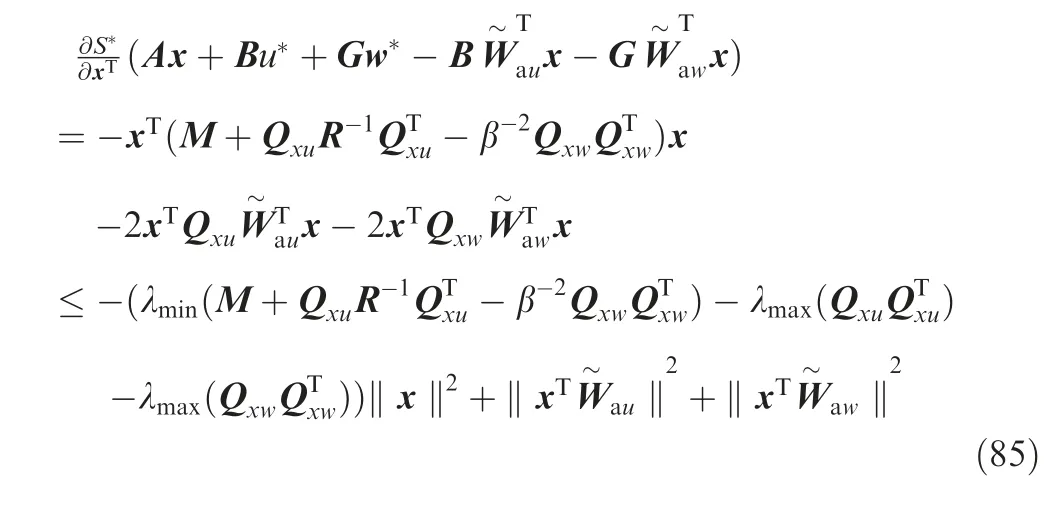
Furthermore, the third and fourth terms on the right-hand side of Eq. (84) satisfy
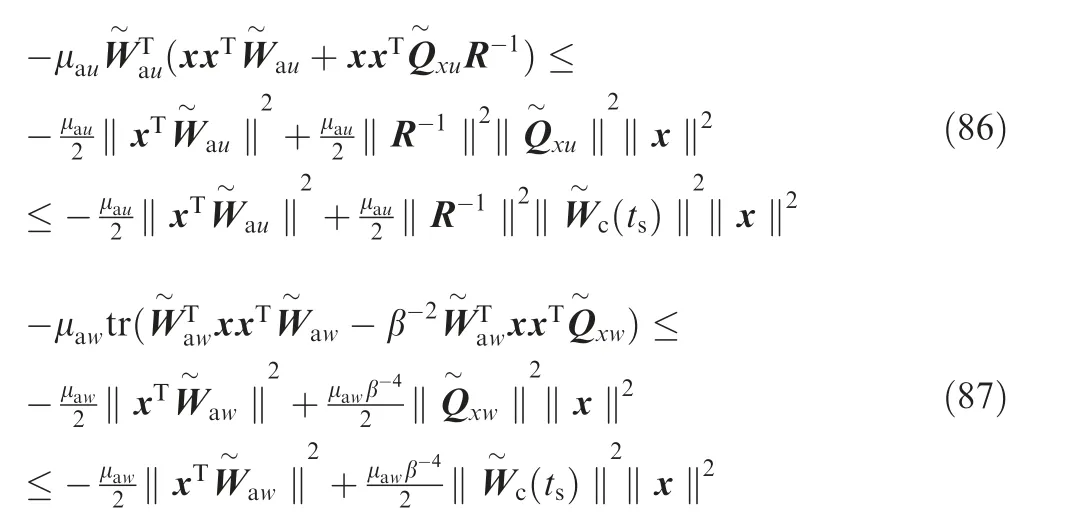
A combination of Eqs. (84-87) delivers
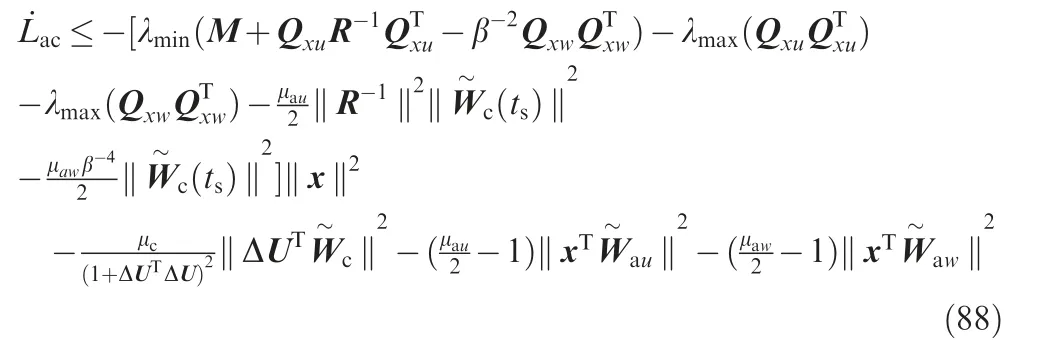
Select the design parameters such that

Then by the standard Lyapunov extension theorem, it can be deduced that all signals of the closed-loop system are bounded, which completes the proof of Theorem 3. Besides,it is noted that S*(x) is non-increasing, which gives
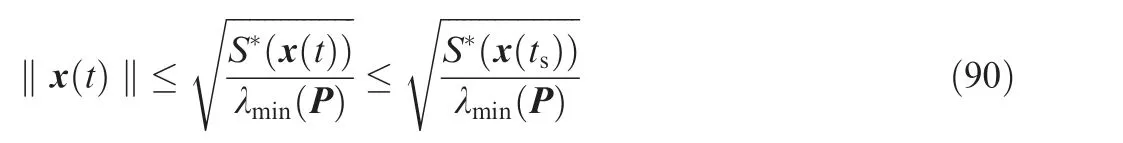
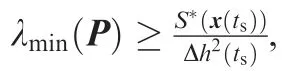
Remark 8. Compared with the existing work, the novelty of our study mainly lies in the controller design for morphing aircraft via a combination of model-based back-stepping method and the model-free Q-learning approach.Correspondingly, the knowledge on the aircraft model can be adopted once available and the advantage of the Q-learning scheme is fully exploited when the model is unknown. In particular, we do not deliberately emphasize on the specific type of Qlearning method or the modification to the existing Q-learning algorithms. Instead, the focus of our work is a union of the back-stepping method and Q-learning approach, which is achieved by the outer part and inner part controller, respectively.In other words,we concentrate on the application of Qlearning technique according to the problem to be solved.The Q-learning scheme utilized here can also be replaced by other reinforcement learning approaches and does not affect the main idea of our work. We approve that there may exit other machine techniques more appropriate for improving the control performance. The specific choice of the machine learning techniques is a topic worthy of further investigation.
Remark 9. As stated in the section of Introduction, the Qlearning methodology has been applied to various classes of nonlinear systems. The aforementioned references mainly focus on the general nonlinear systems and cannot be applied to nonlinear model of morphing aircraft directly since certain assumptions have to be made on the system functions. Particularly,the designed controller based on Q-learning for nonlinear systems cannot ensure stability of the closed-loop system in the presence of disturbances unless certain conditions on the disturbances are satisfied, which make the Q-learning less applicable to the outer part controller design. On the other hand, the outer part controller is devised via back-stepping method with employment of the plant knowledge, where the disturbances are attenuated by adoption of disturbance observers and stability of the closed-loop system can be guaranteed in theory. It is noted that the transient performance is neglected during the back-stepping design process. With the purpose of expediting the altitude tracking control performance, we further design the inner part controller in view of the online learning merit of the Q-learning approach. We also invoke that Q-learning technique is model-free as one of the reinforcement learning methods. However, as stated in Ref.44, the model-free property of the Q-learning method does not lead to the conclusion that the prior plant knowledge on the system model cannot be exploited when the model is in fact available, no matter partially or fully. The system dynamics should be adopted according to the specific conditions. Altogether, the specific applicability of Q-learning to nonlinear control is still an open problem.
4. Numerical simulation
A comparison simulation is conducted to illustrate the effectiveness of the proposed switching control scheme.The parameters and aerodynamic coefficients of the morphing aircraft model are mainly adopted from Ref.18,where 20%uncertainties are considered for the aerodynamic coefficients.The nominal values of the aerodynamic coefficients can be expressed as follows:


Fig. 3 Variation of sweep angle ξ.
The other parameters for three different configurations of the aircraft are shown in Table 1.18
The initial values of the states of system (1) are set as[h0,γ0,α0,q0]=[1000 m,0◦,0.99512◦,0(◦)/s] and the velocity V is assumed to be a constant of 30m/s.The reference altitude hr=1050m, whileandare generated by setting ζh=1 and ωh=0.2. The sweep angle ξ is regarded as a continuous function of h and α so that the lift-drag ratio is optimized by the computational fluid dynamics technique, which is shown in Fig. 3. The external disturbances acting on the γ and q loops are taken as dγ=2e-0.1tsin(0.1t)(◦)/s,dq=10e-0.05tsin(0.2t)(◦)/s2. For the outer part controller design, we select k1=3, k2=5, k3=6, k4=10, ζ1=0.707,ζ2=0.707, ω1=10, ω2=20, εγ=0.1, εz-4=0.1. The design functions φ1γ(·), φ2γ(·), φ1z-4(·) and φ2z-4(·) take linear forms,i.e. φ1γ(x)=l1γx, φ2γ(x)=l2γx, φ1z-4(x)=l1z-4x, φ2z-4(x)=For the inner part controller design, we choose M=diag(1,0.1,0.1,0.1), R=5,β=0.5, Γ=0.05 s, μc=20, μau=5, μaw=5, and the weight values ^Wc, ^Wauand ^Waware initialized in[-0.1,0.1]randomly.It is noteworthy that the inner part controller is trained offline,and the controller switches from the outer part to the inner part when t ≥20 s. The related simulation results are shown in Figs. 4-11, where the proposed method is denoted by m1,the controller with the outer part solely is denoted by m2,and the method in Ref.18is also adopted for comparison,which is denoted by m3.
Fig.4 reveals the altitude tracking performance of all three schemes, which can guarantee the boundedness of the altitude tracking error. We can see that both the m1and m2schemes outperform the m3method in terms of the convergence rate and magnitude of the altitude tracking error. In particular,the m1method has a faster convergence rate than the m2method although a slight overshoot is introduced. The values of states includingγ,α and q are illustrated in Figs. 5-7,whichstay bounded for all three schemes. Moreover, the control inputs are shown in Fig.8,which are all within the magnitude of 30◦. It is noted that the values of states and control inputs after switching are also within a reasonable range. The disturbances dγ,dz-4,and related estimated values are given in Figs.9 and 10, respectively, where the tracking of the actual disturbance signals is achieved in the first 5 s and the estimation errors stay within small bounds thereafter.Finally,the training process of ^Wc, ^Wauand ^Wawis provided in Fig. 11 and norms of the weight estimations converge to steady values within 2 s,which exhibits the effectiveness of the Q-learning method.

Table 1 Morphing aircraft model parameters for three different configurations.
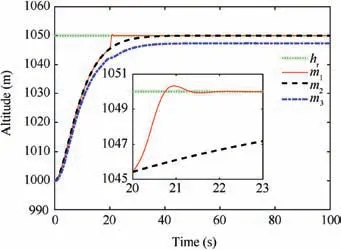
Fig. 4 Response of altitude tracking.
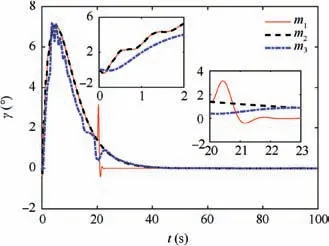
Fig. 5 Response of flight path angle γ.
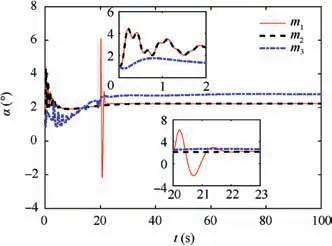
Fig. 6 Response of angle of attack α.
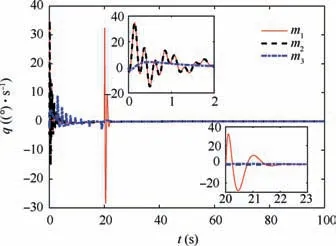
Fig. 7 Response of pitch rate q.
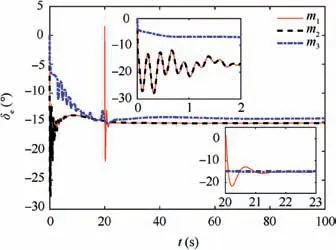
Fig. 8 Control input δe.
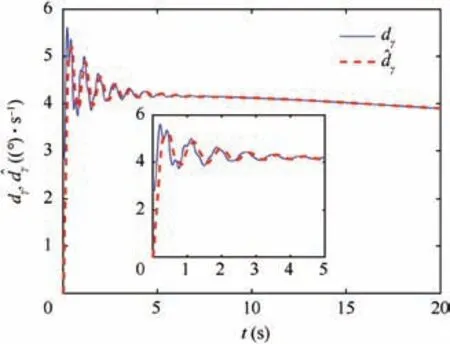
Fig. 9 Disturbance and disturbance estimation in γ loop.
Remark 10. The deflection rate of the elevator for morphing aircraft control is restricted by the servo system, which constitutes the main constraint on the variation of control input. The outer part controller and inner part controller are devised via the back-stepping method and Q-learning technique, respectively. We acknowledge that it is difficult to ensure the smooth transition of the control input as well as the states in theory since the models for designing the two controllers are also different. The idea of this work is to some extent similar with the switching supervisory control studied in Refs.45-47, where a finite family of controllers and a switching signal determining the specific controller are designed. It is noted that the focus of these references is the stability of the closed-loop system and the smooth transition of the controllers is neglected. Two ways of dealing with this issue may be by designing the controller via the linear parameter varying system theory13,or in the presence of both actuator amplitude and rate saturation48-50,which will be the topic of our further study.
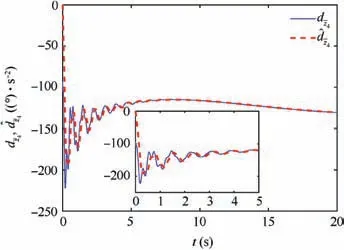
Fig. 10 Disturbance and disturbance estimation in loop.
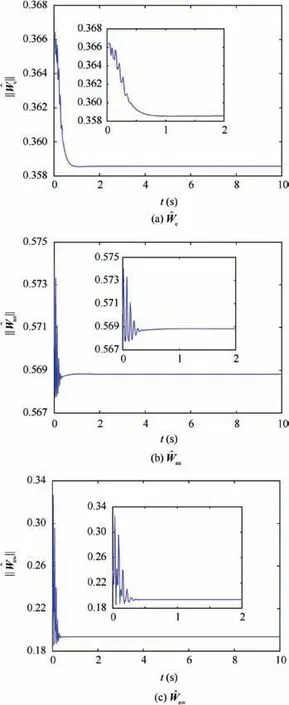
Fig. 11 Response of norm of and
5. Conclusions
(1) The altitude motion model of a morphing aircraft with variable sweep wings is presented, where the morphing process is treated as a function of the system states for enhancement of flight performance.
(2) A switching type controller composed of the outer part and inner part is presented.For the outer part,a combination of the back-stepping method and command filter technique is adopted to avoid the‘explosion of complexity’ problem. Disturbance observers inspired from the idea of ESO are devised along with the exploitation of the integrator structure of the altitude motion model to simplify the back-stepping design.For the inner part,the Q-learning algorithm is developed, which learns the optimal command in the presence of unknown system matrices and disturbances.
(3) The switching of the controller from the outer part to the inner part occurs when the altitude tracking error converges to a small value so that the altitude motion model can be approximated by a linear system. It is proved that the boundedness of all signals of the closed-loop system can be guaranteed,and the controller switches only once.Finally,simulation results show that the proposed scheme can improve transient control performance when compared with the controller which contains the outer part solely.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (Nos. 61873295, 61833016) and the Aeronautical Science Foundation of China (No.2016ZA51011).
Appendix A.
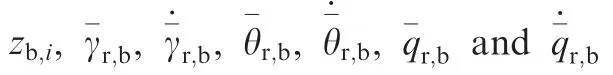
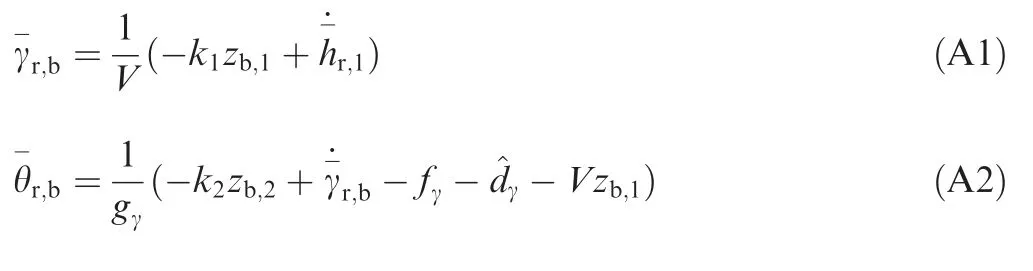
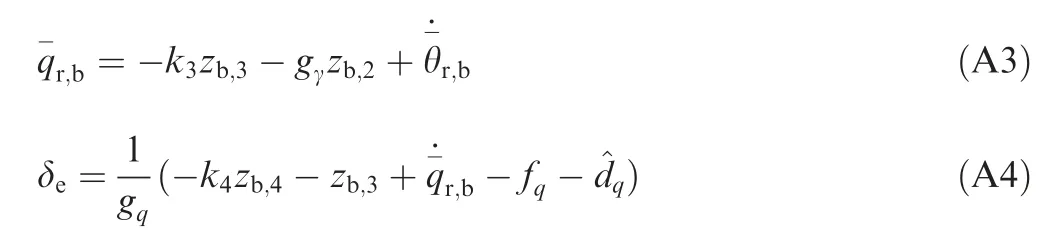
With Eqs. (A1-A4),the time derivatives of zb,ican be written as
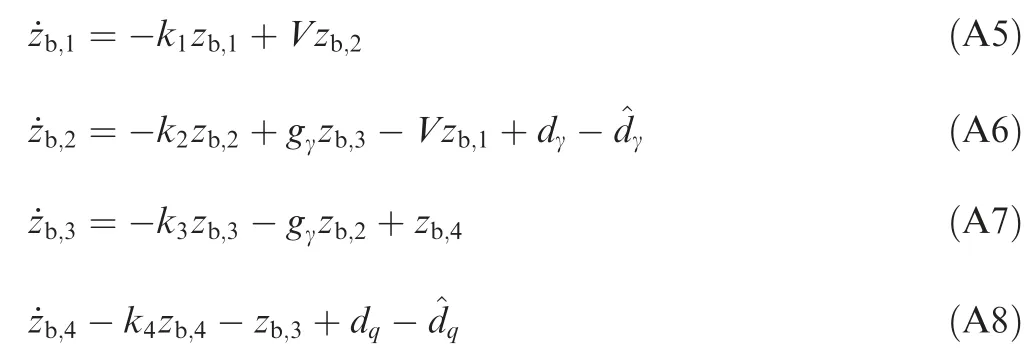
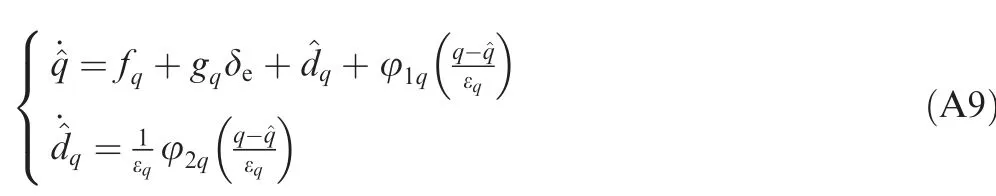
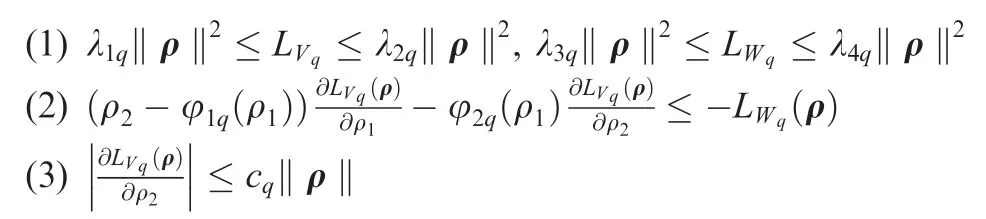
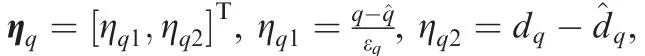
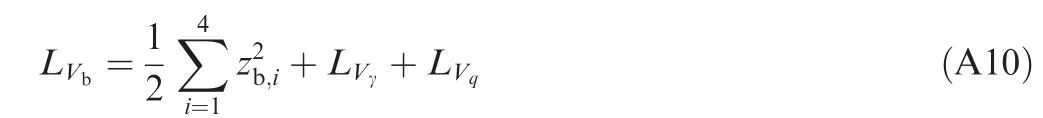
With Eq.(39),the derivative of LVbalong the trajectories of the closed-loop system is given as
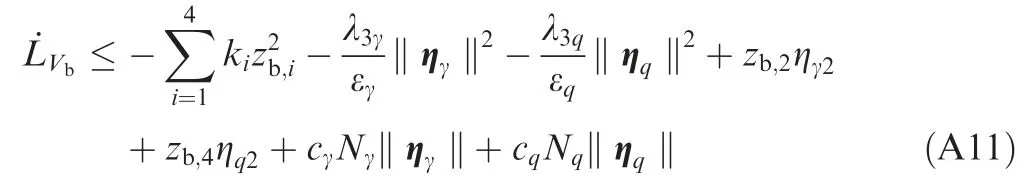
Applying Young’s inequality43to Eq. (A11) entails that
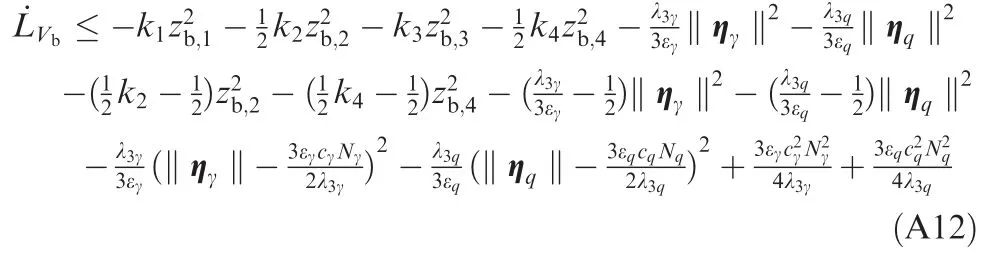
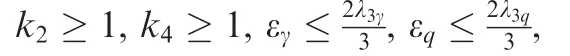
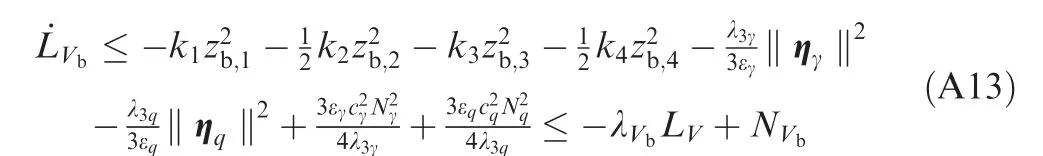
 CHINESE JOURNAL OF AERONAUTICS2020年2期
CHINESE JOURNAL OF AERONAUTICS2020年2期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Delaying stall of morphing wing by periodic trailing-edge deflection
- Optimization and verification of free flight separation similarity law in high-speed wind tunnel
- Non-intrusive reduced-order model for predicting transonic flow with varying geometries
- Consideration on aircraft tire spray when running on wet runways
- Aeroelastic simulation of the first 1.5-stage aeroengine fan at rotating stall
- Experimental study on NOx emission correlation of fuel staged combustion in a LPP combustor at high pressure based on NO-chemiluminescence
