无线传感器网络分布式分簇算法

徐 荣

（安徽广播电视大学 信息工程学院，安徽 合肥 230022）

随着无线传感器网络（WSN：Wireless Sensor Network）的发展，其以低功耗和低成本的特点，正在日益受到人们的关注，并被广泛应用于不同的领域，如健康监测、汽车跟踪等.随着WSN 节点运行，节点能量消耗增加，如何提高WSN 传感器节点能量的利用效率，更好地提高节点的使用寿命，是当前研究的重点.要解决该问题，关键在于构建一个合理的分簇路由协议，以此提高传感器节点中不同节点的能量使用效率.而分簇路由协议的求解，本质是一个NP 难题.在这个难题中，要充分考虑最短传输路径、最小能耗、拓扑结构简单等问题.为解决该问题，谭军（2015）、赵悦（2016）、冉涌（2019）等分别对无线传感器的路由协议进行构建和改进，取得了丰富的经验.但上述研究发现，WSN 网络节点能量消耗还有进一步优化和提升空间.笔者在以往研究的基础上，结合PSO（Particle Swarm Optimization）优化算法的优势，主要从两方面进行探讨：一是构建传感器节点能耗模型，二是对WSN 网络节点中的簇首选择问题进一步探讨和优化.由此，结合上述两方面的工作，解决WSN 中簇首节点能耗不均衡的问题，实现整个WSN 网络节点能耗均衡的目的，提高整个网络节点的使用寿命.

1 WSN 无线网络节点传输能耗模型

1.1 网络模型

出于对问题模型进行简化的目的，将场景设定为长方形网络区域，基站位于区域一侧，各节点随机分布于该区域内，见图1.

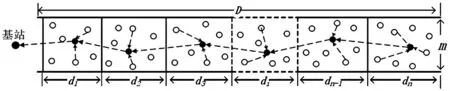
图1 WSN 节点网络模型

该网络中共有N个传感器节点，其节点集合为V={Vi|i=1，2，…，N}，各节点间连线的集合为E=｛（Vi，Vj）|（Vi，Vj）∈V*V，i≠j｝，则网络拓扑结构可被抽象为无向加权图G=（V，E）.

若节点i 的坐标为（Vix，Viy），节点j 的坐标为（Vjx，Vjy），则节点i 与节点j 在二维平面上的距离为：

若节点的通信半径为R，当节点i 与节点j 在二维平面上的距离d（Vi，Vj）不超过通信半径R 时，则节点i 与节点j 互为邻居节点.节点Vi的邻居节点集合为S（Vi）=｛Vj|d（Vi，Vj）≤R｝.

1.2 假设条件

根据研究需要，提出假设：

（1）随机部署各个节点后，每个节点的位置始终保持不变；

（2）不考虑基站电量问题，各个节点为相同的初始能量，由自身电池提供；

（3）各个节点的计算、通信能力以及数据传输有效距离均保持一致；

（4）各个节点均有唯一标识，并且能够获取自身的位置和剩余能量信息.

1.3 能耗模型构建

在WSN 节点传输过程中，主要能量消耗来自节点对数据的发送和接收，且能量消耗随着通信距离的增加而增加.当数据传输的距离为在d，发送的数据为l 比特比的情况下，其消耗的能量为：

同时接收l 比特数据所需要消耗的能量为：

在公式（2）和（3）中，ETx-elec、ETx-amp表示监听数据和信号放大所消耗的能量；ERx-elec、Eelec分别为接收器监听耗费能量和节点接收与发送每比特耗费的能量；εamp为将单位比特数据广播单位面积所耗费的能量.

但是上述的能量消耗模型没有考虑距离的问题，即当传输距离足够大的情况下.如考虑传输距离足够远，那么可以将上述的能耗模型转换为：

在该传输过程中，设置两种传输模式，当d ＜d0时，则采用自由空间能耗模式；当d≥d0时，则采用多径衰减能耗模式.

2 分簇路由算法

分簇路由算法的构建中，主要包括簇的建立和数据传输.其中，簇的建立阶段主要考虑簇的数目、簇首能量消耗等因素，在数据传输阶段主要考虑剩余能量.

2.1 最佳簇首

根据图1 的节点分布图，假设将该区域内的簇划分为K 个，根据上述的能耗模型，得到簇首.而簇首的能量消耗ECH主要包括：接收簇类节点发送的数据消耗能量、接受节点成为簇成员耗费能量、广播自己耗费的能量、数据融合以及融合后传送耗费的能量.同时为简化求解，都采用自由空间模型进行通信.由此，得到簇首消耗的能量：

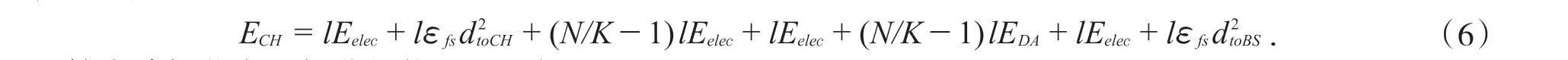
簇内感知节点所耗费的能量ESN为：

根据公式（6）和（7），得到节点工作一轮所耗费的总的能量：

2.2 PSO 簇首优化选举

笔者采用PSO 对最优簇首进行选择，并连同节点所属簇的相关信息全部发送到网络.

2.2.1 粒子群优化算法基本原理

通过观察研究鸟群觅食行为，发现在觅食过程中鸟群的每只鸟都在区域内随机飞行进行搜寻，然后通过在鸟群中共享自身与食物的距离信息，使鸟群中的其他个体调整搜寻路径，在距离食物最近的个体周围进行搜寻.根据鸟群觅食行为提出相应的模拟算法，而实践证明这是一种有效的优化，能够得到复杂问题的最优解.在此基础上不断发展，最终由Kennedy 提出了粒子群优化算法.

假设在给定的目标搜索空间内有m 个粒子节点，粒子群集合为X=｛X1，X2，…，Xm｝，Xi=（Xi1，Xi2，…，XiN），i=1，2，…，m 为第i 个粒子的位置向量，通过适应值函数f（x）计算得到粒子当前的适应值f（Xi），然后可以根据f（Xi）的大小来判断粒子位置向量Xi的优劣.其中，粒子节点数m 的大小直接影响着算法的收敛性和求解速度，应当根据需要解决的问题进行具体设定.

Vi=（Vi1，Vi2，…，ViN） i=1，2，…，m，Vi为 第i 个 粒 子 的 速 度 向 量.Pi=（Pi1，Pi2，…，PiN），i=1，2，…，m，Pi为第i 个粒子当前搜索到的最优位置，即个体极值为粒子群在第t 次循环后搜索到的最优位置，即全局极值pbestt.粒子在空间内跟踪pbesti和pbestt进行搜索，直至达到设定的迭代次数或者误差满足设定条件.

每次迭代后，粒子群中的每个个体将更新自身速度和位置：

其中，c1和c2为学习因子，在［0，2］区间内随机取值；rand（）参数同样在［0，2］区间内随机取值；w为惯性权重.学习因子能够使粒子群中的个体向优秀个体靠近；rand（）参数能够保证群体的多样性；惯性权重能够保证搜索的平衡.

2.2.2 适应度函数构建

为得到最优簇首，笔者以簇首能量因子f1、 簇内紧凑性因子f2、簇首位置因子f3、簇分布均匀性f4作为适应度因子.适应度值最小的作为最优簇首来选择，即：

根据上述的因子，得到适应度函数：

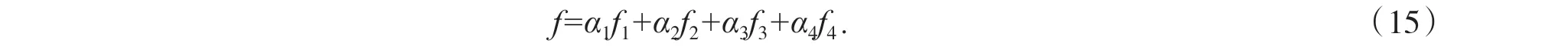
2.2.3 PSO 的适应度函数求解

要求解上述的适应度函数，采用PSO 优化算法进行求解.具体求解步骤如下：

（1）初始化粒子.根据上述的最优簇首计算方法计算网络最佳分簇数Kopt，在粒子群X 集合中每个离子都包含候选簇首中的Kopt个节点，同时对离子的速度、位置等进行初始化.

（2）计算每个离子的适应度值，取适应度值最小的离子作为全局最优解gbest.

（3）更新粒子的速度和位置，使得离子能映射到具体的位置.

（4）更新全局最优和个体最优，再对每个离子的适应度函数值进行计算.

（5）适应度函数值如满足设定的阈值，则终止，如不满足，继续更新粒子速度和位置，并进行适应度值计算.

在上述簇首优化的前提下，分簇路由算法见图2.

图2 最优簇首选举

3 仿真实验

为验证上述算法的正确性和可行性，采用OPNET 软件对上述算法进行模拟.同时为比较本算法的优劣，将本算法与传统的LEACH 协议进行比较.仿真的实验参数Eelec=50 nJ/bit，εfs=10 PJ/bit/m2，区域面积=100 m×100 m，节点数N=100，节点初始能量E0=0.5 J，d0=40 m，εamp=0.001 3 pJ/（bit·m4），数据包 长 度500 bytes，EDA=5 nJ/bit/signal，基 站 坐 标（50，50）.整体节点分布见图3.

通过上述的参数设置，经OPNET 软件仿真，得到图4 和图5 的结果.

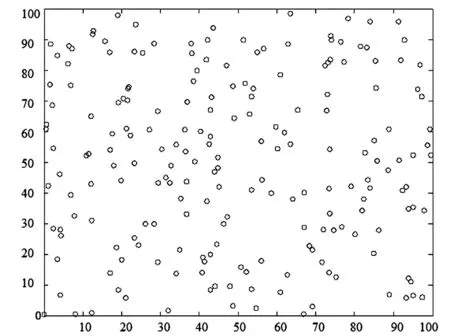
图3 传感器节点分布

图4 网络节点存活数

图5 剩余总能量对比

通过图4 的结果可看出，采用PSO 分簇算法得到的网络节点存活数，从一开始就要高于传统的LEACH 算法，并且第一个死亡节点比LEACH 分簇算法要推迟170 轮.由此说明，经过PSO 算法后，整个网络要多工作两百多轮.

图5 为剩余总能量的对比图.通过图5 可看出，本文提出的算法，具有较小的坡度，而LEACH 算法坡度大.同时在运行轮数方面，本文构建的算法要运行轮数要明显多于传统算法.说明本文构建的分簇算法能耗更小.

4 结语

通过这些研究，分簇算法的本质就是一个NP 求解问题.在这个问题中，结合网络的分布情况，选择最优簇，即可在很大程度上减少数据传输路径，并减少节点的能量消耗，进而最大限度的提高节点的使用寿命.而本文最大的特点在于，采用PSO 算法对簇首的选择进行优化.