基于自适应邻域的固有形状特征算法

石志良，蔡旺月，汪国强，熊林杰

（武汉理工大学机电工程学院，武汉430070）

（∗通信作者电子邮箱1719247190@qq.com）

0 引言

在过去的几十年里，点云扫描设备发展迅速，比如微软的Kinect 传感器，由于其低硬件成本，可以实时提供三维点云和二维图像而应用广泛。2014 年以来，英特尔推出了一系列功能更为强大、更为小型化、成本更低的RealSense 模组，大力推进了机器人、无人机和增强现实/虚拟现实等应用的发展。

点云扫描设备和处理工具的发展促进了研究人员对三维点云的研究，其中物体匹配［1］和识别应用［2］最为广泛。三维物体匹配作为计算机视觉研究的一个重要组成部分，在建模、可视化、识别、分类和场景感知等领域有着广泛应用。基于描述符的三维识别算法通过匹配局部、半局部区域或曲面来匹配两个物体，由于其对杂波和模糊的鲁棒性，已成为三维应用中一种非常有效的方法。但描述符的计算成本通常很高，从点云中所有顶点提取描述符是没有意义的［3］，因此，使用特征点检测算法来提取点云特征点，可仅计算特征点的描述符，从而提高描述符的匹配效率。

基于局部特征的匹配分为两个步骤［4］:1）识别特征点，即根据特征或者显著性的定义而获得三维顶点；2）特征描述与匹配，即基于三维描述符特征点的邻域，将邻域投影到特征空间中，匹配在不同表面上计算的描述符，产生点与点的三维对应。

研究三维点云特征点检测算法的原因不仅仅是因为其作为三维点云应用中的重要一环，还包括以下几点:1）三维点云与三维网格不同，点云数据仅包含三维坐标，或同时包含顶点颜色信息，无拓扑结构，故存储空间小；2）目前特征点检测算法在时间和效率上都不太令人满意，严重限制了检测算法在实际应用中的部署，随着能够获得和处理3D数据的便携式设备增加，效率问题可能变得特别重要；3）三维数据的干扰，即代表同一对象的数据间的点密度变化以及模型和场景之间的维数差异，影响了检测算法的性能。

1 相关工作

1.1 自适应邻域算法

目前，定义点云中一顶点p 的邻域有多种方法，其中最普遍使用的是球邻域、圆柱邻域和k 近邻邻域，如图1 所示。图1（a）表示球邻域由以点p为中心、半径为rs的球体内所有点构成；图1（b）将点投影到一平面上，以点p 的投影点为中心、半径为rc的圆内的点即为圆柱邻域，这里的投影面一般为水平面；图1（c）中k 近邻邻域是指距点p 最近的k 个点。k 近邻邻域定义的邻域与球邻域类似，会产生一个近似的球邻域，这个邻域中顶点数量相同，但k 近邻邻域的近似半径并不固定，对于不同点云，k近邻邻域更具通用性。上述三种邻域均为固定值方式，由于不同点云具有特有且不同的参数值，而且参数的选取过程通常建立在人为经验基础之上，需要反复试探，最终得到主观意识上相对比较正确的值。如图2 所示，在数据采集后，可能存在不同大小（图2（a））、不同点密度的点云（图2（b）），或者一个点云中点密度不均匀（图2（c））的现象，而且每一点周围的几何结构不同，采用固定值方式的邻域定义针对这些情况需手动改变固定邻域的大小，存在诸多局限性。

为了克服上述固定值邻域的局限性，许多研究者大多基于k 近邻邻域和优化的方法寻找最优邻域。Mitra 等［5］提出了一种基于曲率、点密度和法向误差的迭代方法，该方法为了得到最优邻域，需计算设置的参数较多，并依赖于点云的属性。刘鹏等［6］依据所求顶点位置的点云密度，计算了一个合适的动态球半径，但该算法对于稀疏、不规则点云存在一定的缺陷。Mark 等［7］提出了基于曲面变化的方法。Jerome 等［8］提出了基于维度的尺度选择。Weinmann 等［9］提出了基于特征熵的尺度选择，并分析对比了最优邻域的三维场景分类结果与固定值邻域的差异，发现前者更有优势。何鄂龙［10］在特征熵的基础上，提出了一种顾及曲率的自适应邻域（Adaptive Neighborhood，AN）算法。Blomley 等［11］验证了点云中每一点是否应该具有不同大小的邻域。自适应邻域是在固定邻域的基础之上进行最优邻域的选取，理论计算时间增加，但根据以上研究结果，发现虽然计算点云中每个点特有的邻域大小会造成额外的计算时间，但自适应邻域的优点可以弥补其自身造成的时间成本缺陷。

1.2 三维特征点检测算法

随着点云技术的不断发展，点云数据的获取和处理越来越容易。点云是指物体或环境表面的点数据集合，点云与网格模型不同，前者没有额外的拓扑结构，文件存储空间较小，计算过程不需过多顾虑点数量的增减影响计算时间的问题:因为当网格点数据的增加或减少，原先的拓扑结构肯定不再适用，如若计算中需使用拓扑结构，则需重新建立拓扑结构，即3D 表面重建；而点云只需重新建立KDtree 结构，在时间成本上，表面重建的计算成本远多于建立一个KDtree的时间。

三维点云特征点检测算法是计算机视觉研究中识别、分类和场景感知等领域的关键环节，其目的是确定可重复的特征点，以便在视点的变化下，有效地描述和匹配物体。三维特征点检测算法分为两类，即固定尺度检测算法和自适应尺度检测算法。固定尺度算法主要包括修剪和非极大值抑制（Non-Maximum Suppression，NMS）两个步骤，初步挑选出候选特征点，经过非极大值抑制算法，得到最终的特征点集合。与固定尺度检测算法相比，自适应尺度检测算法则需建立和选取尺度空间。

Chen 等［12］提 出 局 部 表 面 补 丁（Local Surface Patches，LSP）算法，基于顶点的最大和最小主曲率来计算顶点的形状指数，并以此来衡量该顶点的显著性:通过计算顶点及其邻域中每一点的形状指数，得到该邻域的平均形状指数，若该顶点的形状指数明显大于或明显小于平均形状指数，则该顶点被保留下来，作为候选特征点。当候选特征点筛选完成之后，对这些点执行NMS；判断一个顶点的形状指数是否为局部极大值或局部极小值，若一个顶点的形状指数全部大于或全部小于其邻域中每一点，则该顶点属于真正的特征点。

Zhong［13］于2009 年提出了固有形状特征（Intrinsic Shape Signatures，ISS）算法。ISS 算法是基于顶点邻域的协方差矩阵的特征值分解来计算顶点的显著性:在修剪阶段，两连续特征值之比均小于阈值的点被保留，并作为候选特征点，其目的是为了满足可重复性，避免检测在主轴方向上具有近似扩散特征的点。在NMS 阶段，显著性取决于最小特征值的大小，若一顶点的最小特征值均小于其邻域中每一点，则该点属于真正的特征点。

Mian 等［14］提 出 了 一 种 称 为 特 征 点 质 量（KeyPoint Quality，KPQ）的三维特征点检测算法，其原理与ISS 算法类似，显著性基于协方差矩阵来衡量，但特征点通过两个主轴长度比与阈值比较来确定。这类似于阈值化的特征值比，与ISS不同的是KPQ 只考虑前两个主方向，得到更多的候选特征点。在NMS 阶段，KPQ 通过经验公式计算得出。Mian 除了提出了固定尺度的方法外，还提出了一种自适应尺度的特征点质量（KPQ-Adaptive-Scale，KPQ-AS）算法。该算法的尺度空间是通过增加邻域大小来建立的，在修剪阶段，KPQ-AS 算使用方法与KPQ 相同。KPQ-AS 与KPQ 的显著性定义相同，但NMS在其选定的尺度上执行。

Sun 等［15］于2009 年 提 出 了 热 核 特 征（Heat Kernel Signature，HKS）的方法:对任何流形，存在一个函数，该函数定义为在时间t内单位热源从一点传递到另一点的热量，称为热核。扩散热量的多少由流形决定。为了将HKS 应用于特征点检测算法，Sun 将显著性定义为较大t 值下的函数值，并选择2环邻域内显著性的局部最大值的顶点作为特征点。

针对自适应尺度检测算法，Unnikrishnan等［16］提出了一种Laplace Beltrami 尺 度 空 间（Laplace Beltrami Scale Space，LBSS）方法:通过不断增加三维网格中每个顶点的邻域大小来计算Laplace-Beltrami 算子，再基于平均曲率和Laplace-Beltrami 算子计算一个常量，并以该常量建立尺度空间，而常量值则用来衡量显著性。

与LBSS 相同，MeshDoG［17］将三维网格作为构建尺度空间的输入。尺度空间是通过应用不同的归一化高斯导数的差分高斯（Difference-of-Gaussians，DoG）算子创建，MeshDoG 不改变网格几何，其中，DoG 的计算可以基于平均曲率或者高斯曲率或者光度信息，而其输出作为顶点的显著性。Bronstein等［18］基于文献［17］的工作提出了一种突出点（Salient Points，SP）的自适应尺度算法，该算法也是一种基于DoG 算子的方法，但它通过改变网格几何建立尺度空间，在不同尺度的滤波之后，检测具有显著位移的顶点作为特征点。

韩磊等［19］针对三维扫描仪获取的点云数据在简化过程中容易丢失模型细节特征这一问题，根据均匀分布点云的特点提出一种自适应点云特征点提取算法，但该算法主要针对均匀点云，耗时长。王庆华等［20］为了有效获取散乱点云中的尖锐特征点和边界特征点，提出一种利用多判据融合的特征点提取算法，主要用于点云精简，计算效率差。

文献［3-4］综述了相关三维特征点检测算法，文献［4］实验算法包括LSP、ISS、KPQ、HKS、MeshDoG、LBSS、KPQ-AS、SP，文献［3］对比了点云库（Point Cloud Library，PCL）中已实现的特征点检测算法:ISS、SIFT3D、Harris3D、SUSAN、Lowe、KLT、Curvature、Noble。文献［4］的研究表明KPQ 的可重复性、区分性和抗噪性表现最好，而ISS 算法在绝对和相对可重复性间具有最好的权衡，效率较高；针对物体识别，MeshDoG和KPQ-AS 表现较好，后者在抗噪性和显著性方面更出色，ISS算法在可重复性上具有较好的结果，只要数据没有太多噪声，ISS是一个可行的方法；在计算成本方面，自适应尺度检测算法明显多于固定尺度检测算法。文献［3］的实验结果表明，ISS 算法在重复性方面比尺度不变特征变换（Scale-Invariant Feature Transform，SIFT）表现更好，但在旋转平移变换下，两种算法在重复性方面都有所下降，且变化明显。根据以上实验结果，发现ISS 算法在可重复性具有较好的表现，但在噪声和旋转平移变换下存在明显的不足。

针对固定尺度和自适应尺度三维特征点检测算法所存在的问题，本文提出一种自适应邻域的ISS 改进算法ANISS，用于检测点云特征点。该方法利用局部特征计算每一点的自适应邻域k 值，并应用于ISS、NMS 算法，得到最终的特征点。ANISS算法不需要手动设置参数，不仅避免了ISS算法因参数设置有误而导致不良的算法效果，而且实验表明，ANISS 算法的可重复性和抗噪性明显优于ISS 算法，且两者的计算效率差异可以忽略不计。

2 ANISS算法

ANISS 算法与ISS算法采用不同的邻域确定方式，由自适应邻域替代球邻域。

2.1 AN算法

AN 算法作为ANISS 算法中关键一环，目的是为点云中的每一顶点找到一个最优的邻域大小。

给定一点云P(pi，i = 0，1，…，n，n ∈N)，则根据点云P 中某一顶点pi的邻域，计算加权协方差矩阵C:

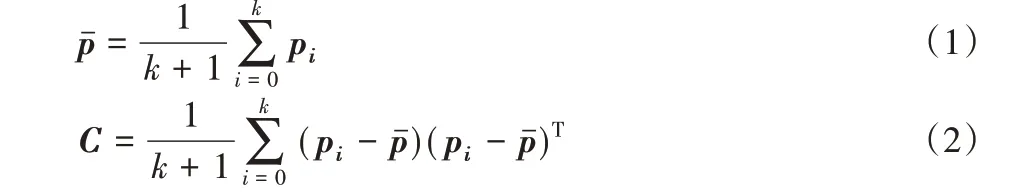
其中:pi是点云P 中第i+1 个顶点；k 是点pi的邻域顶点的个数；pˉ是点pi邻域的几何中心。

矩阵C 是对称正定矩阵，其特征值λ1、λ2、λ3（λ1≥λ2≥λ3≥0）是非负的，并且对应的特征向量v1、v2、v3是正交的。特征值与对应的特征向量实质上描述了一个椭球范围，特征向量代表的是主轴方向，对应的特征值是主轴长度，因此，可以通过特征值来描述局部三维形状。

基于文献［3-5］中自适应邻域算法，提出两种思路:

1）对于尖锐特征使用较小的k 值，对于平坦部位采用较大的k值；

2）在尖锐部位采用较大的k 值，在平坦部位采用较小的k值。

在局部邻域算法中，可能由于邻域大小的改变，尖锐部位邻域信息变化明显，若尖锐部位采用大的k 值，邻域信息更丰富，算法在较大范围里更准确地描述此部位原始形状；在平坦部位由于特征变化不大，邻域大小的改变对原始表面描述的准确性可能影响不大。

三个特征值表示k 近邻邻域的椭球范围的三个主轴长度，λ1是最大的主轴长度，λ3是最小的主轴长度，所提出的AN 算法将用λ3/λ1值来描述此k 近邻邻域的特征大小。给定k 值选取范围[k1，k2]，由于λ3/λ1与最优k 值间的关系未知，因此，给出如下6种计算每一顶点k值的方式:

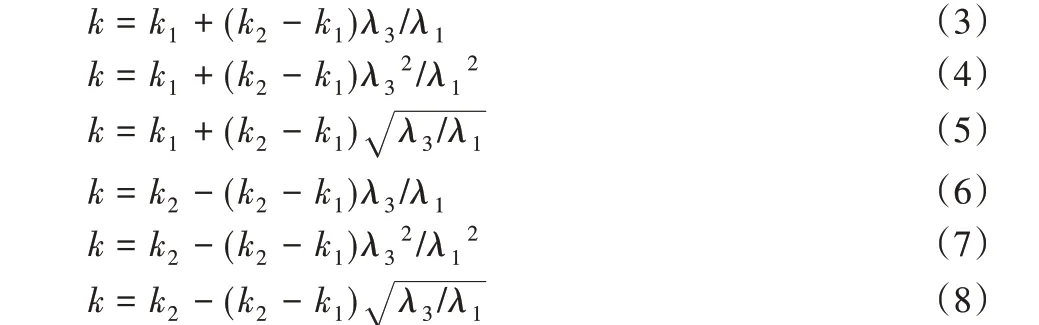
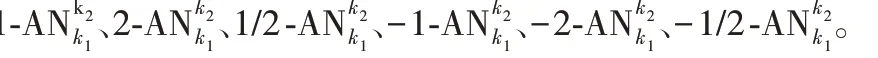
2.2 ANISS算法

给 定 一 点 云 P(pi，i = 1，2，…，n，n ∈N)，点 集 合NEIB(neibj，j = 1，2，…，ki，ki≤n)是点pi的邻域。其中:n 是点云P 的点数量；点neibj是点pi的邻域点；ki是点pi根据AN算法计算的邻域k 值，将AN 算法计算的自适应邻域k 值传递给ISS算法和NMS算法即为AN算法与ISS算法融合过程。图3为ANISS算法判断每一顶点是否为特征点的流程图，主要分为五个步骤:

1）通过AN算法计算每一顶点的自适应邻域ki值。

2）计算点pi邻域中每一点的权重wi:

3）计算点pi邻域的加权协方差矩阵C(pi):

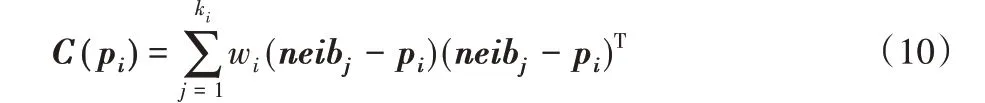
4）计算矩阵C(pi)的特征值λ1、λ2、λ3(λ1≥λ2≥λ3)，判断点pi是否为近似特征点的依据是通过连续特征值间的比值与阈值γ12、γ23相比较，小于阈值则是近似特征点；否则，不为近似特征点。

5）NMS算法。由于点云中特征突出部位的近似特征点分布集中，为了减少信息冗余，将对近似特征点应用NMS 算法，从中提取出最具特征的近似特征点；根据AN 算法计算的邻域k 值，筛选出邻域中最小第三特征值对应的近似特征点，作为真正的特征点。

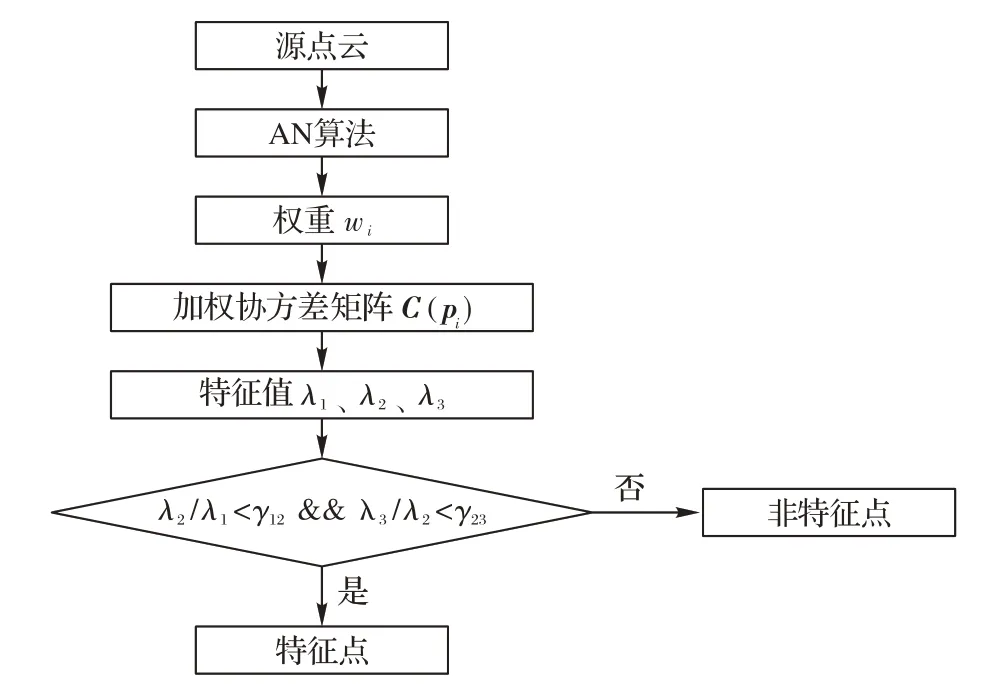
图3 ANISS算法流程Fig. 3 ANISS algorithm flowchart

3 实验与结果分析

实验目的是测试ANISS算法的旋转平移不变性和噪声敏感性，并与ISS 算法进行比较，得到一种最优的ANISS 算法。实验的硬件环境中CPU为IntelCore i7-8700K CPU@3.70 GHz，内存为16.00 GB，主硬盘为120 GB SSD，显卡为NVIDIA GeForce GTX1050 Ti（4 GB），Windows 10 专业版（64 位）操作系统，开 发 环 境 为Visual Studio2013、PCL1.8.0、VTK7.0.0、QT5.7.0。

3.1 点云数据库

为了评估特征点检测算法关于旋转平移的不变性，需生成 本 次 实 验 的 点 云 数 据 库 ，PCL 中 的RenderViewsTesselatedSphere 类可以模拟现实扫描设备，在遮挡、旋转、平移的环境下，扫描得到可见部分的物体点云。以ply 文件作为输入，输出扫描点云。在生成点云的数量上，算法可以设置ply 文件生成扫描点云的数量，共有6 个级别:42、80、162、320、642、1 280，本次实验使用42 这一级别，即在42个不同的视点下，生成42 个扫描点云。基于斯坦福（http://graphics. stanford. edu/data/3Dscanrep/）的2 例模型，每一模型生成42 个不同的扫描点云，图4 为Bunny、Happy 模型的5 个扫描点云。

图4 Bunny、Happy模型的扫描点云Fig.4 Scanning point clouds of Bunny and Happy models

为了模拟环境噪声、添加更加合理的噪声，计算每个点云的分辨率rlt，定义点云中每一顶点与其最近邻距离的平均值为点云的分辨率。利用Boost 算法库，以［0，2rlt］、［0，4rlt］、［0，6rlt］为随机数生成范围，分别生成随机实数，并增加到顶点坐标值中，从而形成不同噪声级别的噪声，这里将噪声级别简称为L2、L4、L6；在L2、L4、L6 级别的基础上，根据每一点云中添加噪声的顶点数量在点云顶点总数中的占比，再次进行级别的划分5%、10%、15%，简称为P5、P10、P15。图5 为整个噪声点云的级别划分示意图，图6 为Bunny、Happy 的原始点云与噪声点云图。

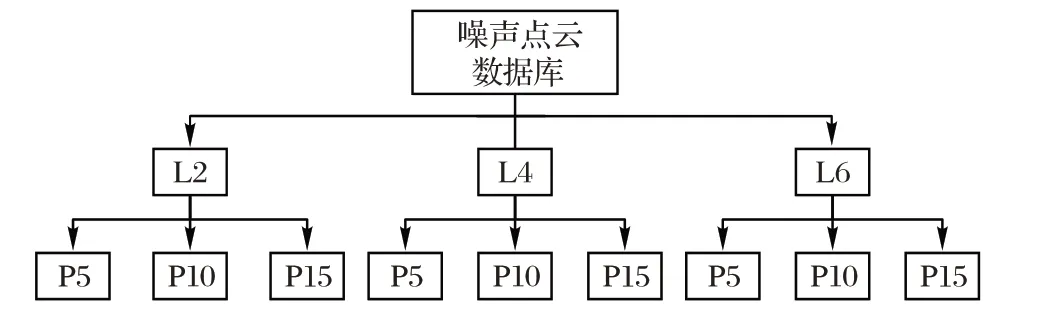
图5 噪声点云的级别划分Fig.5 Level division of noise point cloud

图6 原始点云与噪声点云Fig.6 Original point clouds and noise point clouds

3.2 评价指标

三维特征点检测算法的主要特征是特征性和可重复性:前者是一种能够有效描述和匹配特征点的能力，从而尽可能防止点与点的错误对应；后者是在各种干扰下准确检测相同特征点的能力。实验中刻意强调可重复性的原因有两个:1）可重复性可以给定定义，并可以根据定义评判检测的特征点是否具有可重复性；2）局部形状元素的特征性实际上是场景或模型的一个相对全局的属性，因此很难被局部算法（例如特征点检测算法）所捕获。因此，将可重复性作为三维点云特征点检测算法最重要的特性，以绝对可重复性和相对可重复性作为实验的评价指标。

点云Pos是场景中物体点云在点云OP的对应部位的特征点点云，获得该点云的方法是点云OP的特征点经过旋转平移变换，搜索变换后的特征点在场景点云中的最近邻，若两者距离小于阈值ε1，则该特征点属于点云Pos。其中，阈值ε、ε1均设置为2rlt。

3.3 旋转平移不变性实验与分析

旋转平移不变性实验目的是为了分析特征点检测算法在点云存在旋转平移下的表现情况，并与ISS算法比较。

ISS 算法的参数包括搜索半径、极大值抑制算法半径、γ12、γ23，根据文献［4］，分别设置为6rlt、4rlt、0.975、0.975，ANISS 算法的参数包括极大值抑制算法k值、γ12、γ23。为了保证实验算法的可比较性，更改ANISS算法的极大值抑制算法k值为点云中每一顶点自适应邻域k 值的2/3，两个连续特征值比率的阈值与ISS算法保持一致。

实验以2.1 节中的旋转平移点云为测试数据，以绝对可重复性和相对可重复性为判断依据，对测试数据应用ANISS和ISS 算法，得到各个点云特征点点云的平均绝对可重复性和平均相对可重复性，如表1所示。

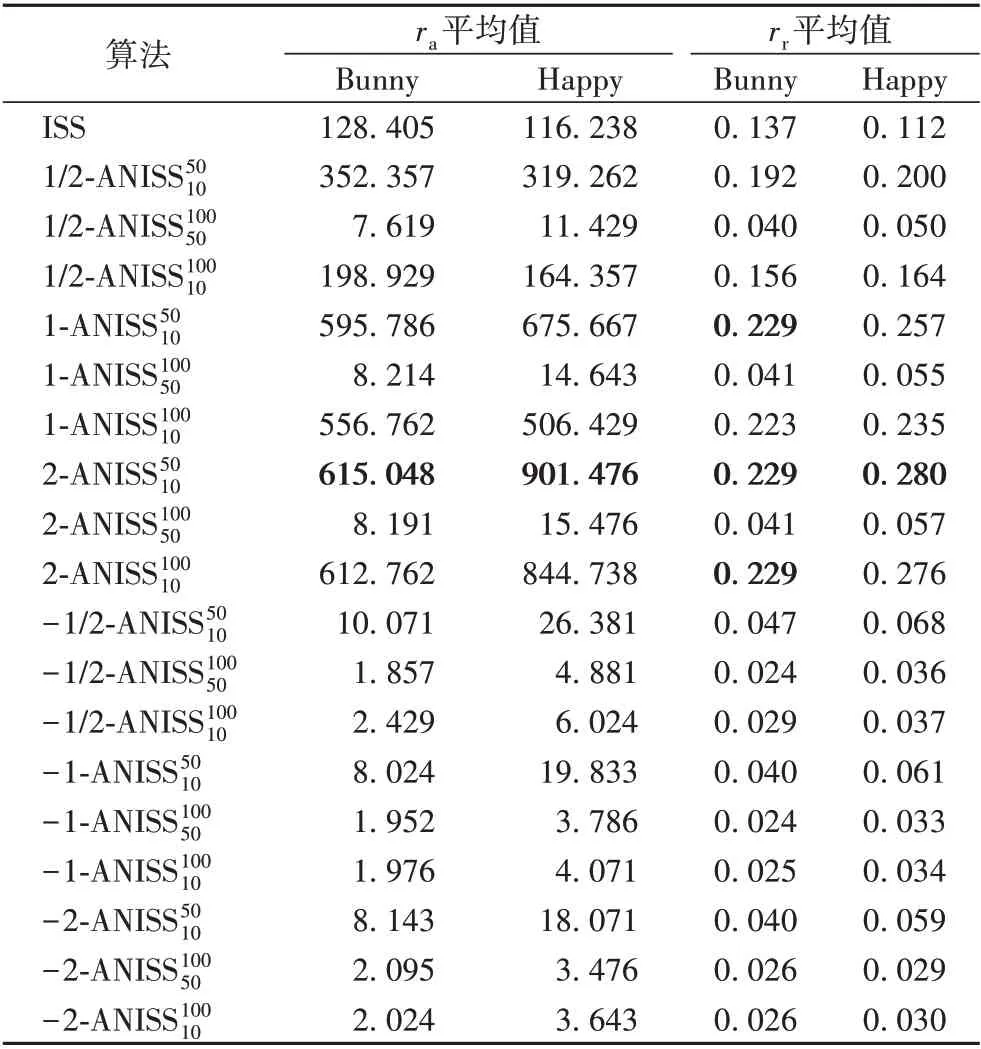
表1 针对旋转平移点云的平均绝对可重复性和平均相对可重复性Tab.1 Average absolute repeatability and average relative repeatability for rotationally translated point clouds

图7 五种算法的特征点检测结果对比Fig.7 Comparison of feature point detection results of five algorithms

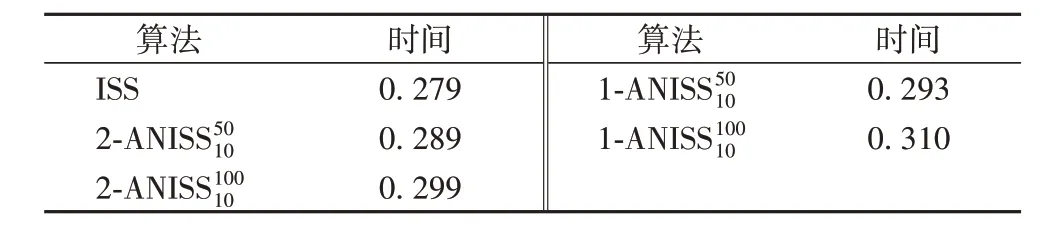
表2 不同算法的平均计算时间对比 单位：sTab.2 Average calculation time comparison of different algorithms unit:s

3.4 噪声敏感性实验与分析

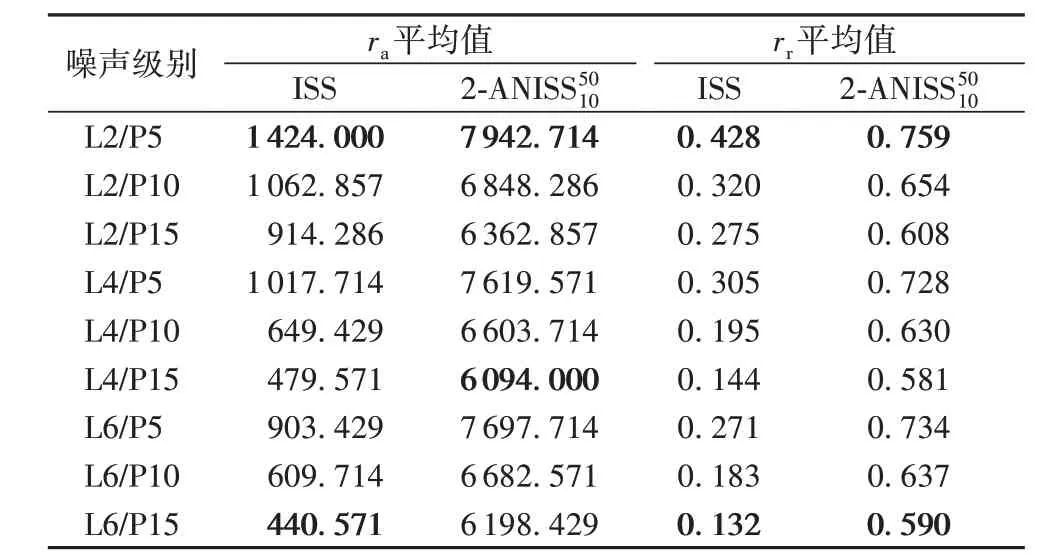
表3 针对噪声点云的平均绝对可重复性和平均相对可重复性Tab.3 Average absolute repeatability and average relative repeatability for noisy point clouds

图8 ISS、ANISS的特征点检测结果对比Fig.8 Comparison of feature point detection results of ISS and ANISS

4 结语

虽然所提算法在一定程度上优于ISS，但导致产生较多的特征点，特征点中可能存在噪声点，对特征描述阶段不利。在后续的工作中，将对特征点数量抑制和抗噪性作进一步研究。