基于区域内容感知核范数的低剂量CT影像去噪

宋 芸，张元科，卢虹冰，邢宇翔，马建华

（1. 曲阜师范大学信息科学与工程学院，山东日照276800；2. 南方医科大学生物医学工程学院，广州510515；3. 空军军医大学生物医学工程系，西安710032；4. 清华大学工程物理系，北京100084）

（∗通信作者电子邮箱lemonzyk@fmmu.edu.cn）

0 引言

计算机断层扫描（Computed Tomography，CT）产生的X 射线辐射暴露能够诱发白血病、癌症以及遗传性等疾病，已在全球范围内引起极大关注［1-3］。为有效降低辐射剂量，临床上最常采用操作是降低数据采集中X 射线管电流量（严格指管电流强度乘以曝光时间，单位为mAs），即低剂量CT（Low-Dose CT，LDCT）扫描。但LDCT 扫描引起的“光子饥饿”现象使得重建后的CT 影像存在严重的伪影噪声［4］，影响诊断结果。另一方面，随着先进影像分析技术的发展，“影像组学”（Radiomics）通过提取医学影像中蕴含的大量高维特征，在临床诊断与疾病预后方面取得突破性的进展［5］。而在影像组学中，影像的纹理细节特征对于分析至关重要。因此，迫切需要一种兼具噪声抑制和纹理细节保持的LDCT影像去噪方法。

针对LDCT 影像中伪影噪声，近年来学者们已提出大量去噪算法，按数据处理不同阶段大致可分为三类:投影域滤波策略、迭代重建策略以及影像域滤波策略。投影域滤波策略直接对原始数据进行平滑滤波，并对滤波后数据采用传统滤波反投影方法（Filtered Back Projection，FBP）方法重建；迭代重建策略［6］通过目标方程对原始数据及重建图像先验进行建模，并采用迭代优化实现高质量成像目的［6-7］；影像域滤波策略直接以FBP 重建影像为处理对象，根据图像局部或非局部结构特征，采用线性或非线性［8-15］方法进行去噪处理。

考虑到当前大部分商用CT 扫描设备仅提供重建后影像数据，为解决现实临床应用问题，本文采用影像域滤波策略，目标是从含有噪声的LDCT 影像y 估计其复原影像x，通常可表示为y = x + e，其中e 表示加性噪声。针对图像中噪声问题，当前去噪算法大致可以分为空间域去噪方法和变换域去噪方法。空间域方法主要是对影像像素灰度值进行处理，如非局部均值滤波、基于块的局部最优维纳滤波［16-17］、全变分（Total Variation，TV）最小化方法［18-20］等；变换域方法是将影像从空间域转换到变换域，通过对变换系数进行规整约束以达到去噪目的，如小波变换［21-22］、三维块匹配滤波（Block Matching 3D，BM3D）［23］、主成分分析（Principle Component Analysis，PCA）变换［24-25］、字典学习［26-28］和变换学习［29］等。

近年来，利用影像的非局部自相似性进行去噪的方法取得了非常好的效果，成为该领域研究热点。该方法通过相似影像块聚类，利用每聚类组内影像块的相关性进行去噪。其中，基于低秩（Low Rank，LR）建模的算法表现出优越的性能［30］。该方法主要包括四步:1）对于每个目标影像块（尺寸为以列向量形式表示）yi∈Rn×1，利用块匹配操作从y 中搜索与其相似的块其中构造数据矩阵其列是的列向量形式；3）计算Yi的低秩近似4）聚合（aggregate）中的影像块（即影像块放回其所在位置并对每像素上的所有影像块取平均值），形成最终影像估计。其中，步骤3）通过最小化目标函数以获取Yi的低秩近似解。这里R(Xi)是秩正则项，当前最常用方法是核范数最小化（Nuclear Norm Minimization，NNM）［31］。NNM 通过对矩阵Yi的每个奇异值进行同等强度约束，在此基础上构建易于计算的凸范数正则项。然而在实际求解中，由于每个奇异值均具有明确的物理意义，即较大奇异值通常表示图像边界轮廓等高能量特征，较小奇异值表示纹理细节等低能量特征，而其余极小奇异值则主要由噪声产生。若对各奇异值进行同等强度约束，则忽略了图像中各结构成分的差异性，难以实现具有纹理保持的图像去噪。此外，不同于自然影像，LDCT影像受原始数据采集及非线性FBP重建过程影响，其噪声为非平稳噪声。传统去噪算法通常并未考虑这一特性，而对影像各区域噪声进行同强度处理，从而进一步加剧影像局部纹理丢失。

针对上述问题，本文提出一种具有区域内容感知能力的加权核范数最小化LDCT 影像去噪算法——rwNNM（regionalcontent-aware weighted NNM）算法。该算法在NNM 基础上，根据影像局部噪声强度以及不同奇异值水平自适应设置核范数权重，从而有效提高核范数的局部信息表达能力，进而提高去噪后影像纹理细节保持能力。其中，为估计LDCT 影像局部噪声，本文结合核范数优化方法，通过利用矩阵奇异值分解（Singular Value Decomposition，SVD）与PCA 的关系，改进了传统噪声估计计算方法，极大提高了计算效率。此外，针对上述步骤1），本文在LDCT 影像局部噪声估计基础上，采用一种新的基于局部统计特性的相似影像块搜索策略，进一步提高了影像块匹配操作的准确性。针对临床肺CT 成像的低剂量仿真数据及真实低剂量数据的实验结果表明，该算法能够在去除LDCT影像噪声的同时，有效保持局部纹理细节信息。

1 本文算法rwNNM

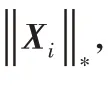
其中:Yi= UΣVT是影像Yi的奇异值分解；Sβ/2(Σ)是在参数β/2下，对角矩阵Σ 的软阈值函数，即对于Σ 中的每个对角元素Σjj，都有

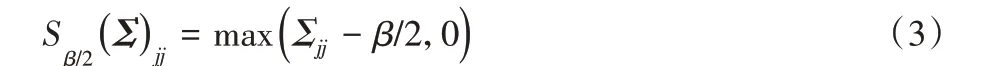
传统的NNM 中，所有奇异值被式（3）以阈值β/2进行同等强度收缩，忽略了LDCT 影像数据矩阵中各奇异值的差异性。而实际中不同奇异值代表影像中不同的结构成分（如影像边界轮廓、纹理细节及噪声等），因此在设计去噪模型时，应根据不同奇异值进行自适应衰减处理，以实现有效去噪的同时保持纹理细节。显然，传统NNM 模型及其相应的求解方法不够灵活，无法处理这些问题。

为了提高核范数的结构表达能力，本文采用如下基于区域内容感知的加权核范数最小化LDCT影像去噪模型:

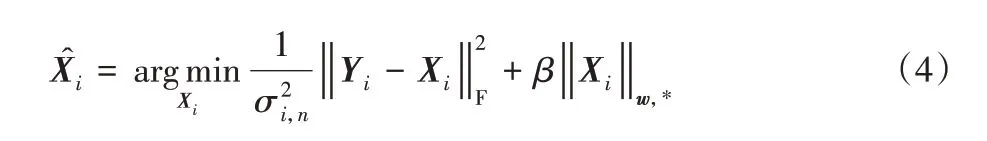
其中:

w =[wi，1，wi，2，…，wi，N]T，wi，j＞0 为赋给λi，j(Xi)的非负权重。该模型通过设置权重向量以增强原始核范数的结构表示能力。其中如何设置权重wi，j及设计相应求解算法是本文重点解决的问题。

1）权重设置。

在LDCT 影像中，较大奇异值表示人体组织结构轮廓信息，较小奇异值表示各组织内容纹理细节信息，而最后极小奇异值则可认为是主要由噪声产生。因此在去噪过程中，应尽可能地保留较大的奇异值（即组织结构信息）；同时需对较小的奇异值进行合理衰减（即去除噪声同时需保持纹理细节）。为此，本文采用一种重加权机制来自适应地调整权重:

2）求解算法。

考虑到式（4）为非凸问题，利用封闭形式解决NNP 问题的子梯度方法［32］已不再适用。文献［34］证明了可以通过加权奇异值软阈值操作得到式（4）的闭合形式最优解:

其中:Yi= UΣVT是数据矩阵Yi的奇异值分解；Sw/2(Σ)是在权重向量w 下对角矩阵Σ 的加权软阈值函数，对于对角矩阵Σ中的每个对角元素Σjj，都有如下加权软阈值函数:

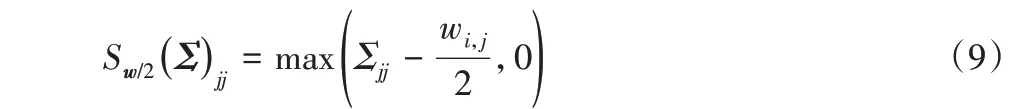
综上所述，本文所提rwNNM算法流程如下。

下面将详细解释算法中所涉及的局部噪声估计以及块匹配操作。

3）局部噪声估计。

由于LDCT 影像噪声为非平稳噪声，因此对局部噪声方差估计能够有效提高算法区域结构及纹理保持能力。为此本文采用文献［24］中提出的基于PCA 的局部噪声方差估计方法估计文献［24］中，噪声估计的思路是首先计算含噪目标影像块矩阵的协方差矩阵并对矩阵进行SVD，然后利用SVD 系数进行噪声近似。该方法需计算协方差矩阵，并对其进行SVD，这极大了增加了算法时间复杂性。为此，本文结合核范数优化方法，利用数据矩阵SVD 及PCA 变换的关系，改进了噪声估计计算方法（即利用数据矩阵Yi的SVD 直接估计，有效提高了计算效率。具体方法如下:

a）假设yi当前目标影像块，通过块匹配操作找到其非局部相似影像块并组成矩阵Yi。

b）对Yi进行SVD:Yi= UΣVT。根据SVD 与PCA 关系（即Yi协方差矩阵公式Cˉ= YYT= UΣ2UT）可知，U 实际可看作Yi做PCA分解的基向量，而其分解系数即为αi= UTYi。

其中:γ为常量；median(·)表示取数据集的中值。

4）块匹配方法。

传统的块匹配方法利用目标影像块yi与待判别影像块y′i间的欧氏距离d2(yi，y′i)，组成相似影像块矩阵Yi。然而由于LDCT影像噪声是非平稳噪声，传统方法难以捕捉非局部影像块之间的相关性，影响块匹配精度。为解决这一问题，本文采用了统计近邻（Statistical Nearest Neighbors，SNN）方法［35］实现块匹配，该方法在欧氏距离的计算过程中，结合影像局部噪声选取相似影像块y′i的判别准则，即:

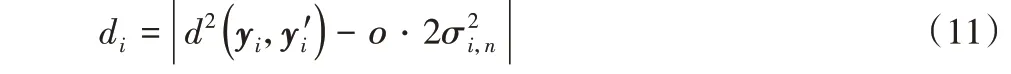
其中:ο是偏移参数。该方法详细过程请参考文献［35］。

2 实验与结果分析

为验证本文所提rwNNM 算法的有效性，对临床肺CT 成像的低剂量仿真数据及真实低剂量临床影像数据进行去噪处理，并与当前具有代表性的NNM 算法［31］、TV 算法［18］、变换学习（Transform Learning，TL）算法［29］进行比较。临床患者均签署书面知情同意书并通过伦理委员会审查。其中:临床患者1 采用Siemens Sensation 16 CT 进行了常规剂量CT（Fulldose CT，FDCT）扫描（管电压120 kVp，管电流100 mAs），该数据用于算法的定量仿真实验；临床患者2 采用Siemens Sensation 16 CT 分别进行了低剂量（管电压120 kVp，管电流20 mAs）和常规剂量（管电压120 kVp，管电流100 mAs）扫描（两次扫描间隔1 个月），该患者数据用于算法的真实临床数据实验。两位患者的其他扫描参数如下:机架旋转一圈0.5 s，螺距1，校准16 × 0.75 mm，扫描层厚5 mm，重建层厚2 mm，重建层间隔1 mm，自动剂量控制功能关闭。文中所有影响均采用两种临床常用显示窗:软组织窗［864，1 264］HU和肺窗［0，1 000］HU。

2.1 参数设置

本文算法参数包括:δ 为迭代正则化参数，实验中设为固定值0.1；γ为噪声估计参数，根据文献［34］建议，实验中设为固定值0.8；ο 为块匹配参数，根据文献［35］建议，实验中设为固定值1；K 为迭代次数，实验中设为10；经反复实验，本文算法影像块尺寸为8× 8，块匹配中非局部相似影像块数量为150。其他算法均根据其相关文献建议选取能够取得最佳效果的参数。

2.2 计算机仿真实验

2.2.1 视觉效果

实验中采用患者1 的常规剂量CT 影像数据（如图1（a））进行数字仿真:首先采用扇形投影并采用上述扫描参数对常规剂量影像进行正投影，然后根据文献［36］方法在投影数据中添加噪声（仿真剂量约为20 mAs），最后进行FBP 重建，如图1（b）所示，从中可发现LDCT 影像中存在明显的条带状非平稳伪影噪声。对比图1 中不同算法的处理结果可发现:NNM、TV 和TL 算法尽管能抑制部分噪声，但是在软组织区域和肺区域仍存在较强的条状伪影噪声，且影像纹理保持较差；本文rwNNM 算法能够在有效去噪的同时保存纹理细节信息，尤其是矩形实线框线内含肺结节感兴趣区。

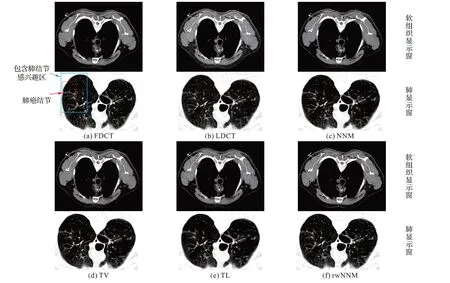
图1 仿真实验结果Fig.1 Simulation results

2.2.2 定量分析

本文采用法向量流（Normal Vector Flow，NVF）［37］、结构相似指标（Structural SIMilarity index，SSIM）［38］和均方根误差（Root Mean Square Error，RMSE）对所提rwNNM 算法进行定量分析。其中，NVF 指标评估各算法处理结果与参考标准FDCT 影像之间的纹理相似性。若算法NVF 中的箭头有序并且与参考影像的NVF 方向一致，表明该算法的细节纹理保存性能较好。图2 为各算法在肺癌结节区域（图1（a）中虚线框内区域）的NVF 影像，从中可看出:相对于NNM、TV 和TL 算法，本文rwNNM 算法所产生的NVF 箭头与参考标准影像的NVF 匹配程度最高，说明rwNNM 算法能够更好地保持影像的细节纹理特征。

本文进一步引入SSIM 和RMSE 对所提rwNNM 算法进行定量分析。其中，RMSE 是表征实验结果准确性的度量指标，而SSIM 则是表征影像结构保持性能的度量指标。所分析区域为包含肺结节的局部感兴趣区。SSIM和RMSE的计算公式如下:

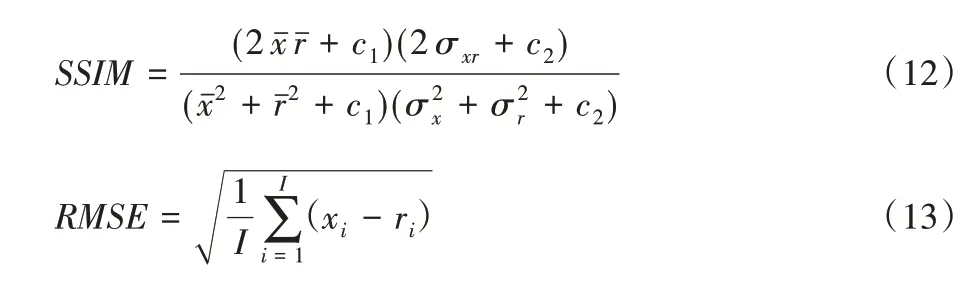
其中:r 和x 分别代表参考仿真模型和实验结果的ROI I 区域；rˉ和xˉ是每个ROI I 区域的平均强度；σr和σx是标准偏差；σxr为参考仿真模型和实验结果之间的协方差；I 代表ROI I 区域中像素的个数；c1=（K1Ls）2和c2=（K2Ls）2为常量，Ls为影像动态范围。根据文献［38］，K1和K2分别设置为0.01 和0.03。各算法的SSIM 和RMSE 定量分析结果如图3 所示。从图3 可看出:本文rwNNM 算法具有最低的RMSE 指标和最高的SSIM指标（两指标分别提高14.38%和8.75%以上），表明本文算法在噪声抑制及结构相似性保持定量指标上优于其他算法。

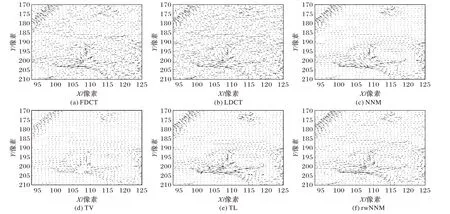
图2 肺结节区域的NVF图Fig.2 NVF images of lung nodule region

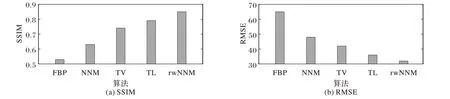
图3 不同算法SSIM和RMSE分析结果Fig.3 Analysis results of RMSE and SSIM of different algorithms

2.3 临床数据实验

本节采用患者2 的120 kVp/20 mAs 低剂量CT 影像进行算法临床LDCT 数据验证。并用该患者一个月后常规剂量扫描数据作为结果评判参考。所有影像均采用两种显示窗:软组织窗［864，1 264］HU和肺窗［0，1 000］HU。

从如图4 所示的不同算法处理结果中可看出:本文rwNNM 算法在处理真实低剂量CT 数据时较其他算法仍能取得更好的噪声抑制以及纹理细节保持效果。

为进一步对rwNNM 算法的临床效果进行定性评估，本文取患者2 的15 个断层采用各算法进行处理，并邀请三位具有5 年以上临床经验的放射医生对不同算法得到的影像结果（从降噪/分辨率/纹理保持三个方面）进行评分，分数范围从0到10（0为最差，10为最好）。为保证客观性，评分过程通过在电脑上随机播放不同算法得到的去噪图像，由每位医生分别评分。最后计算每个算法的平均得分及标准差，如表1 所示。表1结果表明，从临床放射医生角度，rwNNM 算法较NNM、TV和TL算法能够取得更好的临床影像处理效果，且具有显著统计差异性（P＜0.05）。

表1 放射医生对不同算法处理结果的评分（均值±标准差）Tab. 1 Radiologists'scores of the results obtained by different algorithms（mean value±standard deviation）

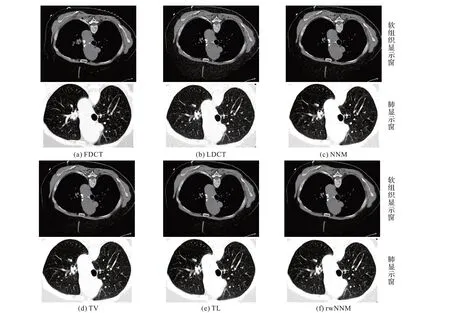
图4 临床实验结果Fig.4 Clinical results

3 结语

本文提出了具有区域内容感知能力的加权核范数最小化LDCT 影像去噪算法，该算法针对低剂量CT 影像的非平稳噪声特点，采用基于局部统计特性的相似影像块搜索策略，根据影像局部噪声强度以及不同奇异值水平自适应设置核范数权重，有效提高核范数的局部信息表达能力，从而提高LDCT 复原后影像的纹理细节保持能力，进而有效提高基于LDCT 影像的临床诊断及影像学分析的准确性。但是该算法在高噪声强度下，LDCT 影像纹理细节保持能力下降。在未来的研究中，将进一步结合LDCT 投影数据的统计特性以及影像局部特性和非局部特性，开展基于区域内容感知能力的加权核范数最小化与变换学习的LDCT影像重建相关研究。