判别式巧解一类最值问题例析

新疆乌鲁木齐市实验学校 (830026) 符强如

引例若正实数m,n满足m+2n=3mn，求m+n的最小值

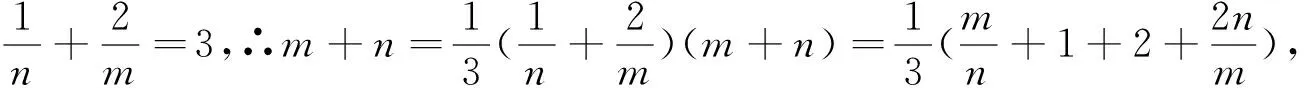
评注:引例的解法多样，有的简洁，有的繁琐，但对一般学生而言都需要较强的技巧.我们可从学生最熟悉的二次方程的判别式来解决.

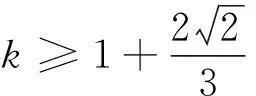
评注:判别式法是由等量关系得到不等关系的一个重要方法.若给定关于x、y的一个二次式，去求解另一个代数式的值或范围，可令所求式子等于k，消去一个变量x(y)，得到一个关于y(x)的一元二次方程，根据题意其判别式大于等于零，即转换成关于k的不等式，求解出k的值(范围)即为所求值(范围)，此方法可称为k值代换法，其本质就是“Δ判断法”，即判别式法.

例1 若实数x,y满足x2+y2+xy=1，求x+y的最大值.

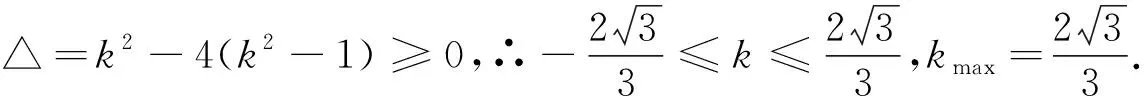
例2 已知实数a,b,c满足a+b+c=0，a2+b2+c2=1，求a的最大值.

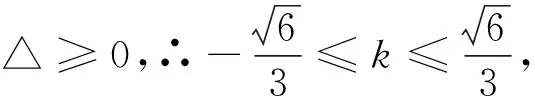
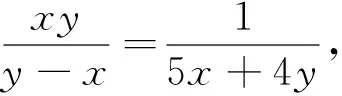
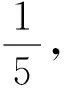
通过以上例题我们不难发现，通过二次方程的判别式方法来巧解这一类双变量的最值问题，能简化推理和运算过程，具有简捷、易想、明快的特点，彰显了化归与转化的思想在解题中的威力.