错因促分析,探索建模型
——以“简单的线性规划问题(一)”教学为例
浙江省玉环中学 (317600) 李林静
一、引言
“简单的线性规划问题”是人教版《普通高中课程标准实验教科书·数学5》第三章教学内容的一部分,该课教学分3课时,本课是第一课时,主要目的是让学生体会数学知识形成过程中所蕴涵的数学思想和方法,掌握处理代数问题的几何方法,体会不等式是解决实际问题的重要数学模型和有效工具,形成良好的思维方式.学习本课之前,学生已掌握不等式的代数解法,及不等式的几何意义,为本节课几何方法作好了铺垫.为此在教学策略上采用问题导向,问题研讨,问题解决等方式实现知识的迁移拓展应用.本课教学目标是了解线性规划的意义及线性规划相关概念;能够正确运用图解法求解简单的线性规划问题;培养学生观察、联想及作图能力,从中渗透数形结合、转化与化归、数学建模等数学思想.
二、教学过程
1.呈现背景,提出问题
引例已知实数x,y满足不等式组


图1
生1:式[(ⅰ)+(ⅱ)]÷2,得0≤x≤2;式[(ⅰ)+(-1)×(ⅱ)]÷2,得0≤y≤2.
生2:画出不等式组所表示的平面区域(图1),得0≤x≤2,0≤y≤2.
设计意图:通过让学生求解x,y的取值范围,巩固前面不等式的相关性质及二元一次不等式(组)与平面区域,分别从代数与几何角度(图解法)进行求解,建构起知识间联系的桥梁,体会数形结合的思想.
(3)4x+2y的取值范围是.
生3:式(ⅰ)×3+(ⅱ),得2≤4x+2y≤10.
生4:在(1)(2)基础上得0≤4x≤8,0≤2y≤4,两不等式相加得0≤4x+2y≤12.
师:为什么两位同学解出的答案不一样呢?
设计意图:问题引导,激发学生寻找原因,引出下面内容:联想激活,寻求方法.一联想前面学过的知识,从代数角度找原因;二引导学生从几何角度寻方法,引出本课课题:简单的线性规划问题(1)——错在哪儿.
2.联想激活,寻求方法
生5:学生4的方法最值取不到,当最大值为12时,x=2,y=2,与已知不等式组中x,y不能同时取到2矛盾,x,y是相互约束的.(巩固取最值时要验证等号是否成立,同时为引出线性规划相关概念作铺垫.)
师:刚才同学们从代数角度进行了分析,能否从几何角度再来分析下原因呢?
提示:同学3是图1条件求解的,同学4是在哪个条件下求解的?请画出该平面区域,并比较两个平面区域来进行错因分析.

图2
设计意图:通过问题导向驱动学生既要会从数的角度分析,也要会从形的角度进行更直观的分析,充分体会数形结合思想在高中数学中的重要性.
师:如何从几何角度(图解法)求解4x+2y的取值范围?
在此之前,先补充线性规划的相关概念:
(1)由x,y的不等式(或方程)组成的不等式组称为x,y的约束条件;
(2)关于x,y的一次不等式(或方程)组成的不等式组称为x,y的线性约束条件;
(3)满足线性约束条件的解(x,y)称为可行解;
(4)所有可行解组成的集合称为可行域;
(5)关于x,y的一次目标函数称为线性目标函数;
(6)使目标函数取得最大值或最小值的可行解称为最优解;
(7)求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题.
师:目标函数4x+2y的几何意义是什么?
设计意图:鼓励学生展开联想,与直线联系起来,引出第三部分:提出猜想,验证猜想.
3.提出猜想,验证猜想
生7:直线;
师:直线是方程式,而4x+2y是什么?
生8:代数式;
师:怎样把目标函数写成方程式?
生9:令z=4x+2y,这样就变成了方程式,从而几何意义就是直线.
师:直线z=4x+2y中z的几何意义是什么?
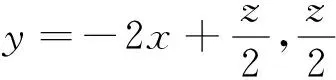
生11:所有这些直线都平行.

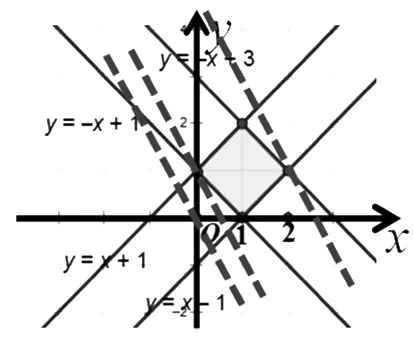
图3
师:不妨动手多画几条直线z=4x+2y,观察一下.
生13:如图3,把这些平行线进行平移,发现在左顶点(0,1)处纵截距有最小值1,即z的最小值为2;在右顶点(2,1)处纵截距有最大值5,即z的最大值为10.
师:在画直线z=4x+2y时,需要画很多条吗?能否简洁一些?
生14:只需先画z=0时的直线,然后经过平移求出其最优解,代入即可得出其最值.
师:是否一定是在最高点处有最值?为什么?
生15:不一定,这与直线的斜率有关系.
师:是否存在x,y,使得z=4x+2y=12?
生16:不存在,因为取定的z必须满足直线z=4x+2y与可行域有公共点.
师:请总结图解法解线性规划问题的一般步骤.
生17:①画出可行域;②画目标函数z=Ax+By=0时的直线,利用平移的方法找出与可行域有公共点且纵截距最大、最小的直线;③根据平移结果,先求区域内特殊点的坐标,再求最优解,最后代入目标函数求出最值.
师:简写为:画、移、求.这样我们分别从数与形两方面分别对目标函数4x+2y的取值范围进行了求解,并总结出了图解法求解线性规划问题的一般步骤;但这里要关注z的几何意义(z与纵截距的相关性),以及最优解不一定在可行域的上下两顶点取到.
师:刚才有同学提出在最高点(1,2)处取到最值,那请同学们自己设计一个目标函数,使得该目标函数在点(1,2)处取到最大值.
生18:目标函数z=x+3y在点(1,2)处取到最大值.
师:还有其他不一样的目标函数吗?
生19:其实这样的目标函数有很多,只要让斜率k满足|k|<1,这个范围内的所有目标函数z=kx+y都可以.
师:能分析下原因吗?
生20:可以设目标函数z=kx+y,经过变形得y=-kx+z,先画y=-kx,经平移及旋转发现,当-k>1时,在点(0,1)处取到最大值;当-k<-1时,在点(2,1)处取到最大值,所以-1<-k<1,即-1 追问:答案完整吗?等号是否取到? 图4 生21:如图4,当-k=1时,在边AD上均取到最大值;当-k=-1时,在边CD上均取到最大值;所以等号成立,所以满足-1≤k≤1的所有k均可以. 师:从研究等号是否成立这个问题中,同学们还发现了什么结论及注意事项? 生22:①当k=±1时目标函数的最优解不唯一;②斜率对最优解的影响. 生23:同学18提出的目标函数z=x+3y中y的系数为3,而同学19提出的目标函数中y的系数为1,这不具有一般性,能推广到一般性吗? 师生同解惑:推广到一般的目标函数z=ax+by,对b进行讨论: 师:在推广到一般性时,我们又发现了什么需要注意的地方? 生24:图解法求目标函数最值要关注z的几何意义(z与纵截距的相关性):若z随截距的增加而增加,称z与截距成正相关;若z随截距的增加而减小,称z与截距成负相关. 设计意图:通过让学生自编目标函数,激发学生学习兴趣,提高学生主动探索的能力,并引导学生探究出以下几点结论: ①在哪里取到最优解有两种思路:可以经过平移得出,也可通过比较斜率大小得出;②在可行域的上下顶点能否取到最值与目标函数的斜率有关系;③最优解不一定唯一;④图解法求目标函数最值要关注z的几何意义. 4.运用巩固,内化迁移 师:大家看到这些阀门图片应该都不陌生,因为家乡是有名的阀门之都,每个工厂经常会遇到资源利用、人力调配、生产安排等问题,这就用到运筹学,而本节线性规划正是运筹学最主要的一部分,通过数学建模把实际问题转化为数学问题来求解,所以线性规划是沟通代数与几何的桥梁,集数与形于一身,下面我们来看具体实例: 例1 某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多从配件厂获得16个A配件和12个B配件,生产一件甲产品获利2万元,生产一件乙产品获利3万元,按每天工作8h计算,采用哪种日生产安排利润最大? 师:面对繁杂冗长的应用题,该如何处理相关信息? 生25:列表: 所需材料产品类型 A配件(≤16)B配件(≤12)耗时t(≤8)甲401乙042 图5 解:设甲、乙两种产品分别日生产x,y件,利润为z,则z=2x+3y,且约束条件为 点评:这里要注意可行域是由整点组成的一个区域,可行域内的所有整点即为所有可行的日生产安排.在可行解为整点且个数比较少时求最值及最优解有无更简洁的方法? 生26:可以直接选择相对较大的(x,y)代入尝试即可得出最值及最优解. 师:请归纳一下图解法求解线性规划实际应用问题的一般步骤. 生27:①根据已知条件写出线性约束条件及目标函数;②画出可行域;③平移目标函数找出与可行域有公共点且纵截距最大、最小的直线;④根据平移结论求出最优解;⑤作出答案(还原成实际问题). 简化为:写、画、移、求、答. 设计意图:对如何求解线性规划问题本节课从课后阅读与思考出发进行了研讨,成功突破一个重难点,而实际应用问题也是本节的一个重难点,这就需要建立数学模型将复杂的实际问题转化为易于理解和操作的数学问题,再利用线性规划求解,使学生在具体情境中感受并由此产生用数学知识解决实际生活中问题的愿望,体会不等式是解决实际问题的重要数学模型和有效工具,形成良好的思维方式,进一步明确数学问题源于生活并可用于生活,学好数学的目的在于应用. 5.回顾反思,拓展问题 请总结一下我们这节课学到了哪些知识(构建知识框架)? 课后作业:教材P91:练习1,2; 练习3 已知函数f(x)=ax2-c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围; 练习4 设等差数列{an}的前n项和为Sn,若S4≥10,S5≤15,求a4的最大值. 设计意图:通过课本练习1巩固图解法求解线性规划的一般步骤,并再次理解最优解不一定在上下顶点取到,以及目标函数z的几何意义;通过课本练习2促使学生面对实际应用问题该如何处理,明白数学源于生活,也应用于生活;另外补充了两道练习,学生猛一看是前面知识内容,自然而然会用前面知识求解,这两道练习的目的是激发学生创设观察、比较、归纳、探究老题新做,促使学生用线性规划去求解,发现一题多解,多题归一;另一方面提示学生在学习中要学会新旧知识之间的融汇贯通,及时去归纳总结,反思提升,建立起新旧知识间的桥梁. “数据分析、数学建模”是高中数学六大核心素养的一部分.如何使该核心素养落实到教学实处?本课采用问题导学的方式激发学生的认知结构,建立新旧知识间的联系,促使学生从数、形两方面学会数据分析,推理错误原因.利用问题串来调控教学,鼓励学生发现问题,质疑探索,拓展问题,培养学生的问题意识、反思意识.通过解决问题、自编题目、推广问题、归纳总结等灵活的教学手段,发展学生认识数学知识背后的一些通性通法,提高学生的逻辑思维能力;并引导学生面对繁杂冗长的实际应用问题,能够建立相应的数学模型进行求解;通过课堂小结驱动学生建构起本节内容的知识框架;以及通过课下作业促使学生发现新旧知识间的联系,提升学生归纳总结、一题多解、多题归一的能力.因此设计有效的课堂教学内容,创设导学功能强的问题,激发学生深入探索知识间的联系和数学思想,探索数学学习的基本方法和步骤,达到对数学知识和概念的深入理解,是落实数学核心素养目标的基本途径,也是核心素养下数学课堂教学追求的高度.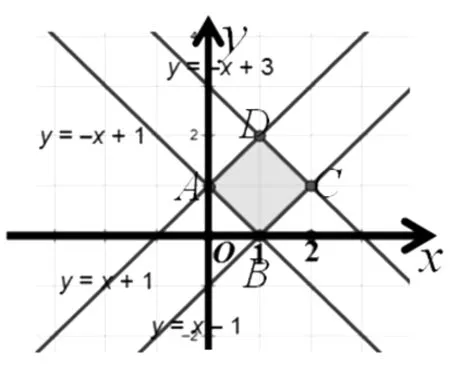
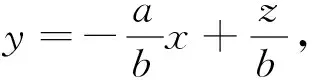


三、教后反思

