基于BFGS-FA优化的分数阶灰色模型的中长期负荷预测

(1.国家电网公司西南分部， 四川成都610065；2.四川大学电气工程学院， 四川成都610065)

0 引言

负荷预测是利用当前已知的信息包括历史信息、现状及未来的发展趋势，对未来的负荷做出判断的过程。可以满足各类负荷需求，从而为社会发展提供动力[1]。负荷预测的精准度决定了相关发电单位的发电成本以及供电可靠性，出现超载预测会使得发电单位的发电成本增加；出现欠载预测会使得供电可靠性受到影响[2]。由于中长期的负荷受到各种不确定因素的影响，而且相关数据的收集较短期负荷预测来说更加困难，所以一般中长期负荷预测的预测精度相对较差。因此，提出适当的方法以提高中长期负荷预测的精度具有很大的实用价值[3],保证整个系统保持稳定且高效地运行，以满足用户的需求[4]。其中灰色模型由于其处理小样本、贫信息的特点在电力系统中长期负荷预测中得到了广泛的运用。近年来提出了许多新形式的灰色模型，包括采用扩展、优化以及修正的方法，以达到更好的预测效果。常见的预测算法有时间序列建模[5]、模糊预测方法[6-7]、支持向量机[8-10]。文献[11]针对灰色模型在预测增长较快的负荷时预测效果差的问题提出把发展系数和灰色作用量看成是随时间而变的变数，从而提出了自适应粒子群优化灰色模型的负荷预测方法。文献[12]提出利用Elman神经网络结合灰色模型进行中长期负荷预测，提高灰色模型的适应能力。文献[13]提出基于粒子群算法的变权缓冲灰色模型，提高了拟合的稳定性。文献[14]在分析灰色模型已有研究现状和不足之处的情况下提出了构造新型灰色预测模型。文献[15]在文献[14]的研究上提出采用分数阶灰色预测法应用于负荷预测。

本文提出了一种基于拟牛顿—萤火虫算法(broyden fletcher goldfarb shanno-firefly algorithm，BFGS-FA)优化的分数阶灰色模型的电力系统中长期负荷预测的方法。该方法用分数阶灰色模型代替原有的整数阶灰色模型，解决了新信息优先使用的问题，增加了模型的自由度和灵活度。通过采用实例仿真证明，基于BFGS-FA优化的分数阶灰色预测的组合模型可以提高负荷预测的预测精度，达到更好的预测效果。

1 分数阶灰色预测模型

从电网规划的角度来看，对于电力系统的中长期负荷预测具有预测样本少的特点，选择预测模型时有一定的局限性，而且尽量回避对模型数据量要求高的预测模型。灰色系统可以运用“小样本”、“贫信息”不确定性系统为研究对象，因此，可以在电力系统中长期负荷预测中使用灰色模型。

现有的灰色模型主要是基于一阶累加生成序列建模，然后通过一阶累减得到预测值[14,16-19]。但其预测模型为一个指数函数，这就意味着当输入样本的波动较大时，其预测的精度会降低。分数阶灰色预测模型是在分数阶累加生成与分数阶累减生成的基础上建立的。通过对累加生成算子的阶数进行调整，根据调整的阶数生成目标序列，以提高灰色预测模型的拟合精度[14]。

设原始数据序列为：X(0)=(x(0)(1),x(0)(2),…,x(0)(n),r∈R+)，X(r)=(x(r)(1),x(r)(2),…,x(r)(n))为原始数列的r阶累加数列。分数阶灰色模型为:

x(r-1)(k)+az(r)(k)=b,

(1)

其中：

(2)

(3)

其中，Y，B分别为

(4)

(5)

其值为公式(6)所示：

(6)

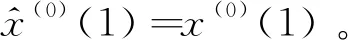
分数阶灰色模型有着整数阶灰色模型不能代替的优点，在相同的情况下，分数阶灰色模型与整数阶灰色模型相比满足信息优先，扰动界小等优点[20]，这些优点使得分数阶灰色模型在负荷预测中克服了整数阶灰色模型的缺点，从而使得预测的结果比整数阶灰色模型的精确度有明显的提高。

2 BFGS-FA优化的分数阶灰色模型

2.1 BFGS-FA原理

从分数阶灰色预测模型的原理可以看出分数阶运算主要体现在数据的预处理过程中，阶数的选取会影响分数阶灰色模型的预测准确性，因此寻找最优的阶数十分重要。近几年提出了许多的优化算法，包括最速下降法、粒子群算法、自适应粒子群算法、遗传算法、模拟退火算法等。由于萤火虫算法(firefly algorithm，FA)具有全局寻优的能力，相比于其他算法而言，在收敛条件发生变化时可以克服局部最优的问题。但FA在优化的后期收敛慢，收敛精度不高，为克服FA的缺陷，文献[1]提出了利用数值效果较好的拟牛顿法(broyden fletcher goldfarb shanno， BFGS)算法，将该算法使用在FA迭代更新过程中，以增强其局部寻优能力和收敛速度。

BFGS-FA算法的基本实现步骤如下：

Step 1：初始化FA算法基本参数，萤火虫数目、最大吸引度、光强吸收系数、步长因子、最大迭代次数或搜索精度；

Step 2：随机初始萤火虫的位置，计算萤火虫的目标函数值作为各自最大萤火虫亮度I：I(r)=I0e-γr2，相互吸引度：β(r)=β0e-γr2；

Step 3：以萤火虫的亮度升序排列种群；以萤火虫亮度向量第一个数值为最优值；

Step 4：移动所有萤火虫的位置到更佳位置，利用BFGS更新萤火虫的位置；

Step 5：是否满足收敛条件，若满足条件，则结束输出最优，否则，转Step2。

2.2 BFGS-FA优化的分数阶灰色模型的负荷预测

利用分数阶灰色预测模型进行中长期负荷预测，可以拓展灰色预测的应用范围，提高灰色模型的抗干扰能力。而分数阶灰色预测模型的重点在于阶数r值的寻取，r值的不同会导致预测结果有很大的区别。本文采用BFGS-FA算法的全局收敛性和超线性收敛速度的特性寻取分数阶灰色预测模型的最佳阶数，可以提高分数阶灰色预测模型的准确性。

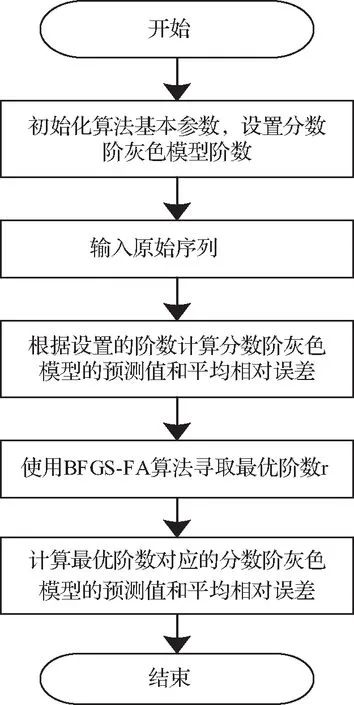
图1 基于BFGS-FA优化的分数阶灰色模型的负荷预测基本流程图Fig.1 Basic flow chart of load forecasting based on fractional gray model optimized by BFGS-FA

基于BFGS-FA优化的分数阶灰色模型的负荷预测基本流程图如图1所示。利用BFGS-FA算法优化分数阶灰色预测模型的具体步骤如下：

求解分数阶灰色预测模型的最优阶数，即在于求解出r满足以下优化问题：

(7)

Step 1：初始化算法基本参数，设置分数阶的灰色模型的阶数ri，给定用于计算的灰色预测的原始数据X(0)=(x(0)(1),x(0)(2),…,x(0)(n),r∈R+)；

Step 2：分别通过阶数ri，计算分数阶灰色模型的预测值且计算对应的平均相对误差f(ri)；

Step 2.1：计算原始数据构成序列X(0)的ri阶累加生成序列X(ri)；

Step 2.2：对X(ri)按式(3)生成序列Z(ri)；

Step 2.3：计算X(ri)的累减生成X(ri-1)；

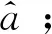
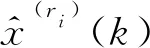
Step 2.6：根据式(5)计算X(ri)的模拟值；

Step2.8：按式(7)计算平均相对误差f(ri)；

Step 3：计算适应度函数Fi；并利用函数Fi确定萤火虫的光强Ii；

Step 4：计算ri之间的距离Mij：

(8)

新ri：

(9)

Step 5：计算适应度函数f(ri)；

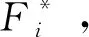
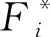
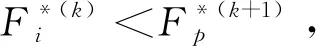
Step 9：判断算法收敛准则是否满足，若满足，则结束，反之，转Step 3。

Step 10：通过最佳阶数rp计算分数阶灰色模型的预测值作为输出值。

3 实例分析

为验证本文提出方法的有效性与实用性，由于本文研究对象为中长期的负荷预测，因此选取某地1998年～2012年的售电量作为原始数据进行仿真。分析原始数据可以得出，原始数据并非光滑的曲线，大致趋势呈现出指数增长，可以使用灰色模型进行预测。利用MATLAB软件平台进行仿真，以1998年～2009年数据作为输入数据进行建模，以2010年～2012年数据作为预测的检验值，用以检验预测结果的准确性。采用残差εi和平均相对误差MAPE作为比较依据：

(10)

(11)

对于分数阶灰色模型而言，阶数的选取也是十分重要的环节，本文采用BFGS-FA算法进行最优阶数的寻取。不同阶数的分数阶灰色预测模型对应的仿真结果如表1所示，残差对比如图2所示。

表1 不同阶数的分数阶灰色模型的仿真结果Tab.1 Simulation result of different order of gray model

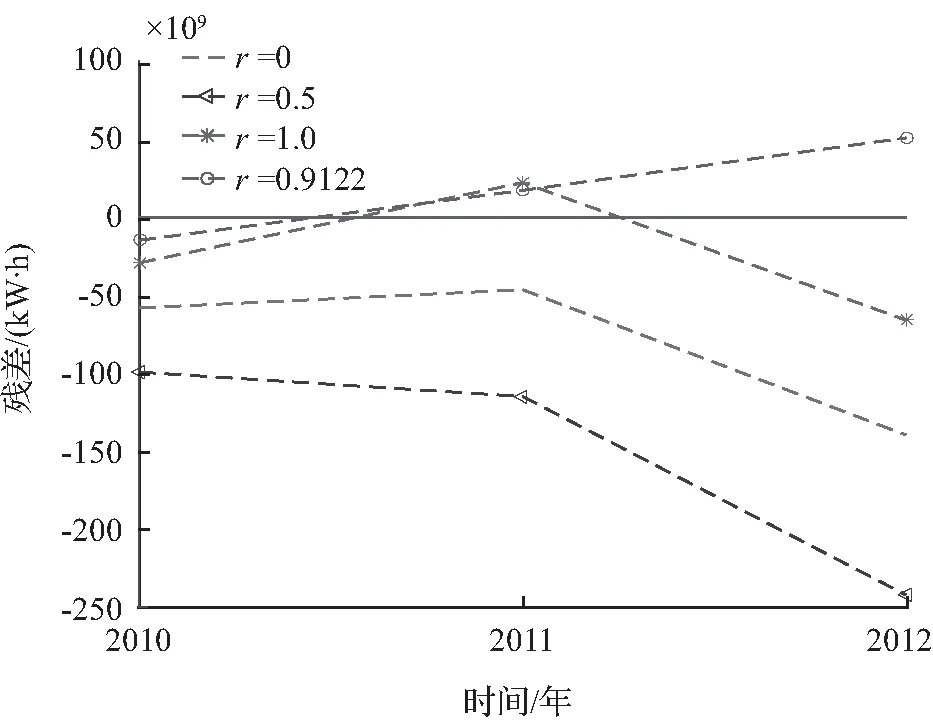
图2 不同阶数的分数阶灰色模型仿真结果残差对比图Fig.2 Residuals comparison chart of simulation results of fractional gray models with different orders

从表1可以看出，不同阶数的分数阶灰色模型对应的仿真结果不同。当r=0时，平均相对误差为4.16 %；当r=0.5时，平均相对误差为7.80 %；当r=1时，平均相对误差为2.00 %；通过BFGS-FA优化后选取的阶数r=0.912 2时，平均相对误差为1.40 %，误差最小。从图2也可以看出，当r=0.912 2时，残差较其他阶数的灰色模型的更加小，预测结果更加精确。

为了验证本文所提方法有效性，本文还对GM(1，1)模型、文献[11]提出的自适应粒子群优化灰色模型、文献[12]提出的灰色Elman神经网络模型进行仿真，将得出的仿真数据与本文所提出模型进行对比。在MATLAB平台上的仿真结果如表2所示，仿真结果对比如图3所示。

分析表2，对于2010年～2012年数据的预测结果分析可得，GM(1，1)模型的平均相对误差为4.39 %。自适应粒子群优化灰色模型的平均相对误差为2.46 %，灰色Elman神经网络模型的平均相对误差为3.00 %，其相对误差具有一定的波动性，2001年～2003年误差很小，但2004年相对误差达到20.64 %，由于突变的历史数据使神经网络算法训练数据时未能捕捉其到动态性变化规律，可以将GM(1，1)预测值和Elman神经网络残差预测值结合得到最终优化结果。而对于分数阶灰色预测模型，通过BFGS-FA算法优化阶数，r=0.912 2时，平均相对误差为1.40 %。可以得出，本文提出的模型较这三种模型来说，效果更好。

图3(a)为本文方法的预测值与实际值的对比图；图3(b)为本文方法与GM(1，1)模型预测值的对比图；图3(c)为本文方法与自适应粒子群优化灰色模型预测值的对比图；图3(d)为本文方法与灰色Elman神经网络模型预测值的对比图。从仿真结果对比图3可以分析得出本文算法相对于其他算法来说预测精度有了进一步提升。

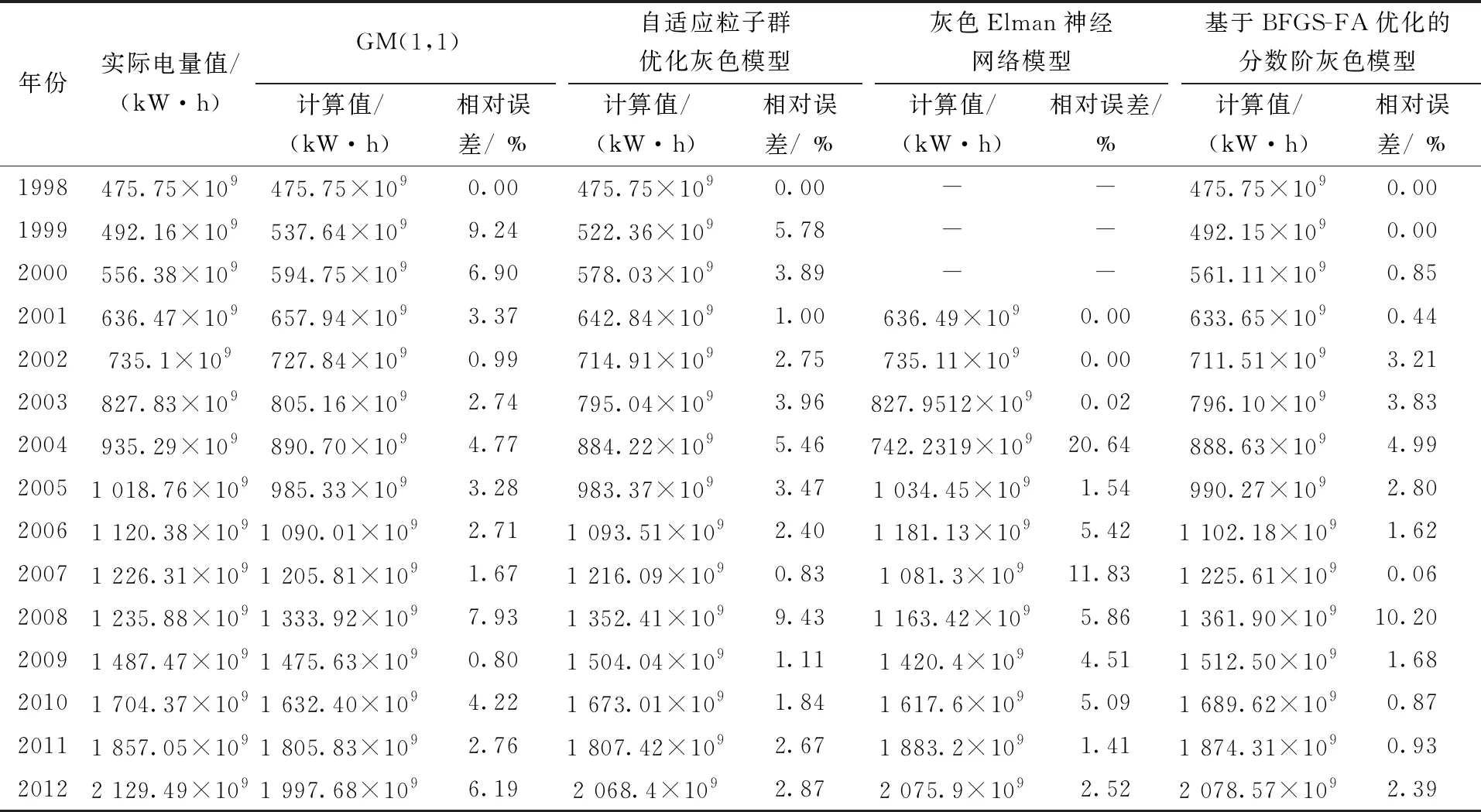
表2 实际值与模型计算值的比较Tab.2 Comparison between the actual data and data of models

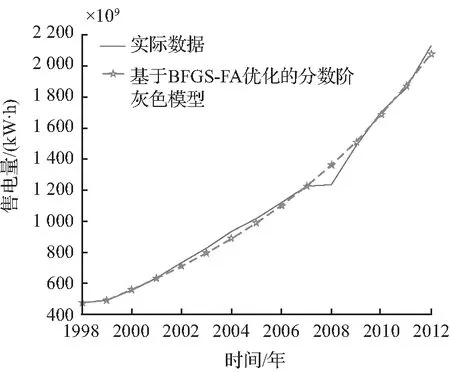
(a) BFGS-FA预测效果图

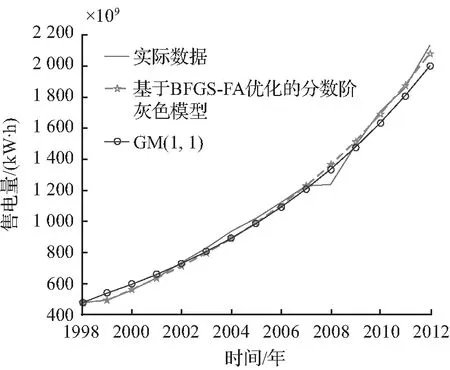
(b) BFGS-FA与GM(1,1)预测效果对比图

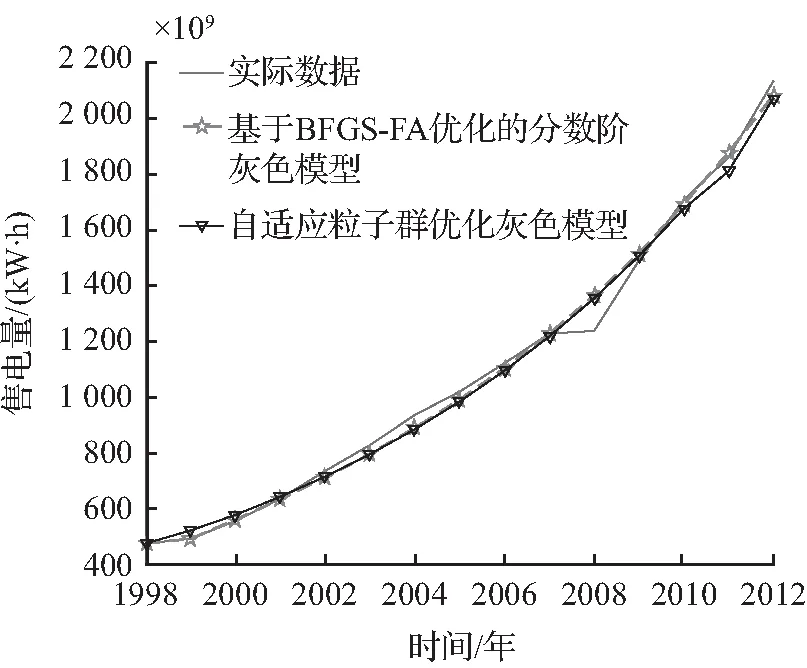
(c) BFGS-FA与粒子群优化预测效果对比图

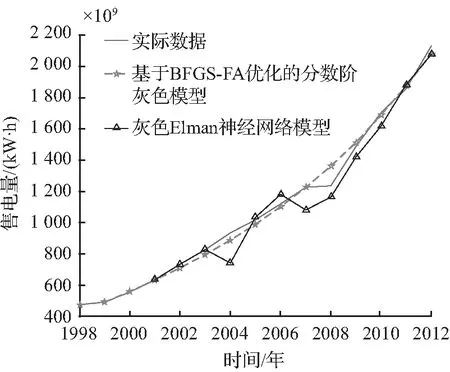
(d) BFGS-FA与Elman预测效果对比图

图3 仿真结果对比
Fig.3 Comparison between simulation results

4 结论

本文提出了一种利用BFGS-FA算法优化的分数阶灰色模型的电力系统中长期负荷预测方法，利用分数阶灰色模型代替了传统的GM(1，1)模型，这样不仅可以增加灰色模型运用的自由度，减少由于输入样本数据的波动带来的扰动界变大的问题，还可以优先利用新信息，使得在进行负荷预测的时候优先考虑新信息的变化带来的影响。考虑到BFGS-FA算法在寻优时始终朝着最优的方向搜寻，收敛速度快，具有全局寻优的能力，可以克服大部分算法易陷入局部最优的问题的特性，将该优化算法用于优化分数阶灰色模型，提升了分数阶灰色模型的应用效果。通过实例分析结果表明，本文所提方法较传统灰色模型、自适应粒子群优化灰色模型和灰色Elman神经网络模型在电力系统中长期负荷预测的准确性方面有着明显的提升。