低压电网绝缘检测装置的设计分析

张秀华1，荆栋2

(1.山东工业职业学院电气工程系， 山东淄博256414；2.山东理工大学交通与车辆工程学院， 山东淄博255049)

0 引言

电网的绝缘电阻和分布电容，是涉及电网安全运行的重要参数，必须经常进行测量。目前，针对电网绝缘参数的测试方法主要有：附加直流电源的电缆绝缘在线监测法[1]、直流检测法[2]、相对地附加电容法[3]、多路绝缘电阻自动检测法[4]、注入信号法[5]、不平衡电压实时测量法等[6]。直流检测法能够区分电网的对地电容和绝缘电阻，但测试过程存在危险。其他测量方法均忽略了对地绝缘电阻的影响，以系统的全绝缘阻抗来近似逼近对地电容，从而使绝缘参数的测量产生误差。另外，现有测量方法在计算过程中附加元件均参加运算，其标称值与实际值误差直接影响计算的精确度[7-8]。本文通过对低压电网串联谐振回路的运行分析，提出了利用附加接地电阻来实现电网绝缘参数的在线测量，论证不同线制下低压电网绝缘检测装置设计遵从的一般原则，为今后此类设计提供设计依据。

1 检测装置结构原理

图1 检测装置原理结构图 Fig.1 Principle and structure diagram of detection device

图1为单相绝缘检测装置原理结构图，L1、L2是绕在同一个高导磁铁芯上的两组线圈电感，工作磁通未饱和，近似为线性电感[9]，且M=L1=L2=L；并联电容相等C1=C2=C；L1C1和L2C2构成双谐振电路，Rr为测试电阻，Z为线路负载。电路正常运行情况下，开关S断开，铁芯中的磁通为零，电源电压Usinωt全部加在负载两端，双谐振电路的串入不影响线路的正常工作。测试条件下，开关S闭合，铁芯中的磁通不为零，选择适当的L、C，使其发生并联谐振或在谐振点附近工作，其阻抗很大，使测试电流很小甚至为零，从而保证了测试的安全性。

2 检测装置设计分析

2.1 检测方法的可行性分析

为理论分析问题方便，选取测试点在低压电网出线，暂忽略电网对地绝缘电阻r和分布电容C0的影响，论证检测方法的安全性与可靠性，检测电路拓扑图如图2所示。

图2 电路模型拓扑图Fig.2 Circuit model topology

① 测试过程的安全性分析

列写测试状态下的网络方程，由KCL和KVL得到关系式(1)、(2)：

(1)

(2)

由电感电容元件的电压电流关系得关系式(3)(4)：

(3)

(4)

考虑工程实际情况，对于2 kW负载Z，电感电流约为10 A，电感内阻R0约为0.1Ω[10]，因此，在双谐振条件2ω2LC=1下，化简式(1)～式(4)并用工程近似处理法得测试状态下的网络方程满足关系式(5)：

(5)

② 测试过程的可靠性分析

测试条件下，暂忽略电感内阻R0的影响，由双谐振电路运行条件(2ω2LC=1)得方程(6)：

(6)

2.2 设计参数分析

考虑电感直流电阻R0，附加测试电阻Rr以及电网对地绝缘电阻r和对地分布电容C0，检测电路的拓扑图如图3所示。

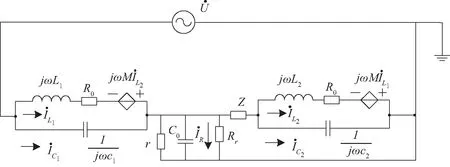
图3 检测电路拓扑图Fig.3 Detection circuit topology

列写图3网络方程得关系式(7)(8)：

(7)

(8)

且由KCL及电感、电容元件的电压、电流关系得方程(9)、(10)、(11)：

(9)

(10)

(11)

(12)

(13)

解方程(13)则谐振参数电容C电感L、电感线圈的内阻R0以及角频率ω与对地绝缘电阻r和分布电容C0之间满足函数关系式(14)、(15)，即：

(14)

(15)

2.3 三相供电参数设计分析

低压供电方式还有三相三线和三相四线两种[11-12]。

① 利用2.2的推导得三相三线供电方式下测试电流的表达式(16)为：

(16)

对式(16)求解条件极值，则三谐振电路下谐振参数电容C电感L、电感线圈的内阻R0以及角频率ω与对地绝缘电阻r和分布电容C0之间满足函数关系(17)、(18)即：

(17)

(18)

② 对应2.2的推导得三相四线供电方式下测试电流的表达式(19)为：

(19)

对式(19)求解条件极值，则四谐振电路下谐振参数电容C电感L、电感线圈的内阻R0以及角频率ω与对地绝缘电阻r和分布电容C0之间满足函数关系如式(20)、(21)所示：

(20)

(21)

由上述分析可见：对于不同线制的低压电网而言，谐振点的选取主要取决于电感值的大小，与电容的变化关系很小。并且由不同线制下电感的表达式可知：若线制取为N，则电网绝缘电阻r与谐振电感值满足关系式(22)。针对不同线制的低压电网，谐振电容和电感在设计时参数是已知的，电感线圈的内阻可以测定，如此以来便可计算出电网对地绝缘电阻的大小。在式(22)的基础上利用关系式(23)可以计算出电网分布电容的大小。

(22)

(23)

3 仿真试验

根据上述理论推导结果，针对低压电网单相供电和三相供电的实际运行情况[13]，利用系统仿真软件编写仿真程序，进行仿真试验。

3.1 单相供电情况下系统运行仿真测试

设计双谐振电路电感L=5.1 H，直流电阻R0=0.2 Ω，电容C=0.98 μF；附加测试电阻Rr=1 kΩ；负载Z=100 H；电源电压幅值为310 V，电源频率为50 Hz；编写系统仿真程序对图3进行仿真测试，测试结果如图4、图5所示。

① 双谐振电路测试电流I(Rr)的仿真结果见图4。

图4 双谐振电路中测试电流Fig.4 Testing current in double resonance circuit

② 双谐振电路电源电压U(1)、电容两端电压U(1)-U(2)、负载两端电压U(2)-U(4)的仿真测试结果见图5。

由图4、图5的仿真结果可见，双谐振电路中，测试电流在10 ms之内降至10 mA以下，保证了测试的安全性；并且电源电压与负载电压相等，测试过程不影响负载的运行，保证了测试过程中供电的可靠性。

③ 双谐振电路中绝缘电阻的测试结果见表1。

图5 双谐振电路中电源电压U(1)、电容两端电压U(1)-U(2)、负载两端电压U(2)-U(4)Fig.5 Voltage supply U(1)、capacitor voltage at both ends U(1)-U(2)、load terminal voltage U(2)-U(4) in double resonance circuit

表1 不同电源电压下仿真结果Tab.1 Simulation results in different supply voltages

由表1仿真结果可见，改变电源电压的大小不影响绝缘电阻的安全准确测试。

3.2 三相供电情况下系统运行仿真测试

① 三谐振电路两端相电压的仿真结果见图6：

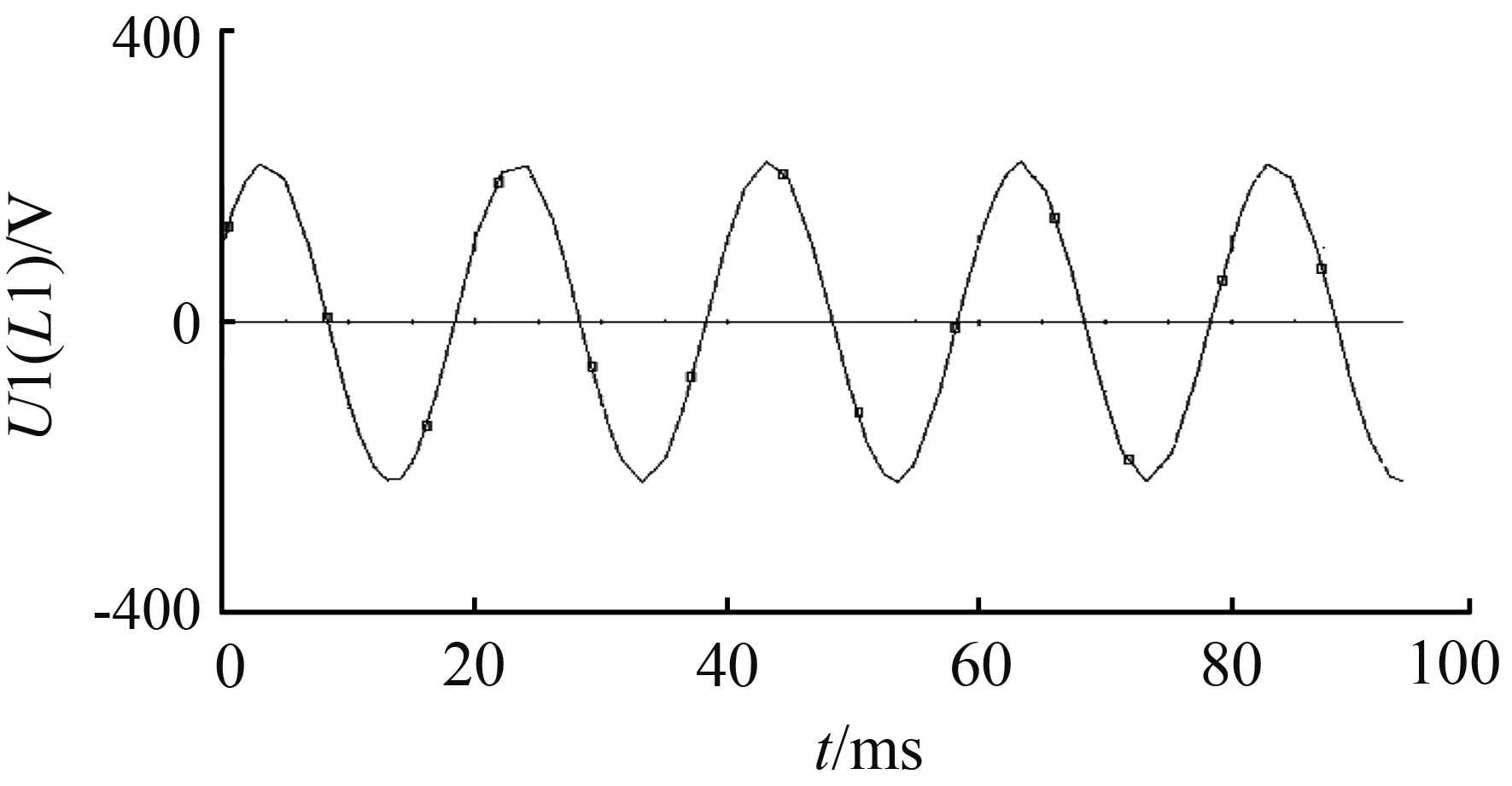
(a) 三谐振电路入端相电压U1(L1)

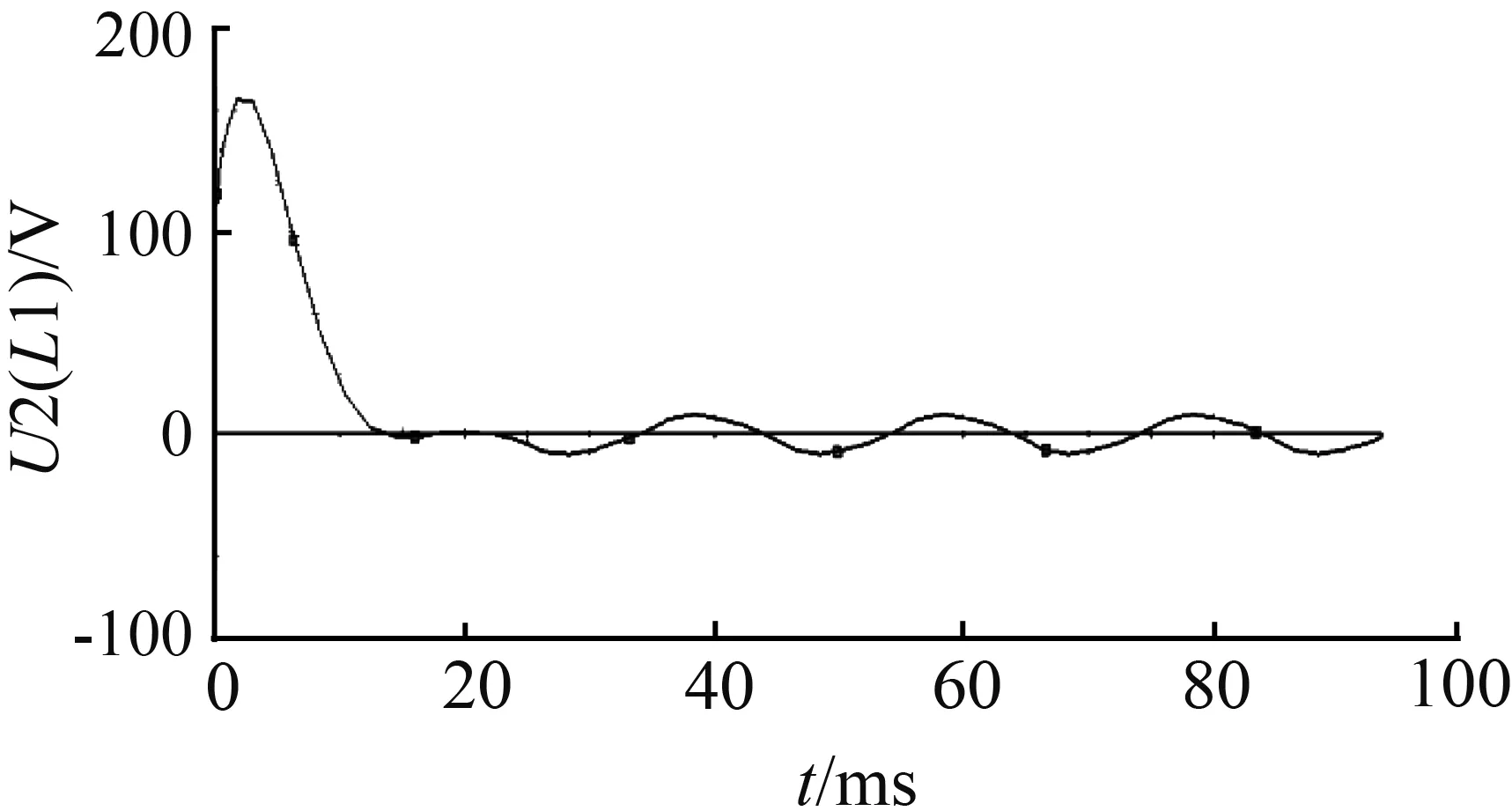
(b) 三谐振电路出端相电压U2(L1)

图6 三谐振电路两端相电压
Fig.6 Phase voltage at both ends of the three resonance circuits

② 三谐振电路测试电流I(Rr)仿真结果见图7。

图7 三谐振电路测试电流Fig.7 Testing current in the three resonance circuits

对比图6、图7的仿真结果可见：测试环境下，三谐振电路的测试相电压由220 V降到10 V左右，测试电流大约为6 mA，从而保证了测试的安全。

③ 三谐振电路中绝缘电阻的仿真测试

调节三相电源电压在50～380 V取值，仿真结果与双谐振电路仿真测试结论基本一致；改变测试电阻Rr，在200～1 600 Ω取值，测试结果见表2，由表2仿真结果可见改变测试电阻的大小不影响绝缘电阻的安全准确测试。

表2 不同测试电阻下仿真结果Tab.2 Simulation results in different test resistances

④ 不同线制下仿真测试

不同线制下仿真结果见表3，由表3仿真结果可见改变低压线制不影响绝缘电阻的安全准确测试。

表3 不同线制下仿真结果Tab.3 Simulation results in different line systems

上述仿真结果可见：低压电网绝缘电阻测试结果不受测试电压大小、测试电阻大小以及线制的影响，均可实现安全在线准确地测试。对电网分布电容的测试可以在绝缘电阻测试基础上利用关系式(23)计算求解。

4 结论

① 低压供电网络串联谐振系统，谐振电容、电感和对地绝缘电阻、分布电容之间存在线性数学关系，利用附加电阻构成单相接地，选取合理的谐振电容电感参数，可以在线安全地测试出电网绝缘参数值。

② 绝缘阻抗的计算公式中不含附加电阻，附加电阻不参与绝缘参数的计算，不影响绝缘参数的计算结果。附加电阻测量绝缘参数的误差在±0.5 %以内，测试精度高。

③ 不同线制的低压电网绝缘参数满足一定的数学关系，此理论推导结论在低压电网绝缘检测装置设计中具有通用性。

④ 基于附加电阻测量方法的计算公式，利用单片机很容易实现电网绝缘阻抗测量的智能化，为电网绝缘的智能检测提供理论依据。