无轴承开关磁阻电机凸极转子封盖优化设计

(河海大学能源与电气学院， 江苏南京211100)

0 引言

无轴承开关磁阻电机(bearingless switched reluctance motor, BSRM)兼有磁悬浮轴承与传统开关磁阻电机的优点，在高速驱动领域具有广阔应用前景[1-5]。然而相比于圆柱形电机转子，高速工况下BSRM凸极转子与气隙空气摩擦剧烈，继而引发较大的风摩转矩与风摩损耗，降低效率，因而有必要在分析BSRM气隙空气流场的基础上，研究可降低风摩损耗的凸极转子外型优化设计方法。

目前已有学者针对抑制开关磁阻电机凸极转子风摩损耗问题，提出了圆柱外型转子[5-6]。然而圆柱外型转子在转子外表面增加了额外的肋部，将导致齿极间漏磁问题，且高速工况下易变形。亦有学者提出在凸极转子两侧加装封盖以降低风摩损耗[7]。文献[8]在此基础上采用计算流体动力学(computational fluid dynamics, CFD)法论证了凸极转子两侧加装封盖抑制风摩损耗的原理，为提高转子散热性能，提出了局部封闭的凸极转子结构，在降低风摩损耗的同时改善转子对流换热状况，封盖尺寸越大，转子风摩损耗抑制效果越明显，而转子散热状况越差[5]。可见二者存在矛盾关系，因此有必要选取最优的封盖尺寸，对凸极转子封盖优化设计，在降低风摩损耗的同时尽可能提高转子散热性能。

本文在上述研究基础上，利用CFD法对BSRM凸极转子气隙空气流场进行了数值求解，分析了不同封盖尺寸对抑制风摩损耗的影响，并对流场网格进行了划分，分析了相应的3D气隙流场，计算了不同封盖尺寸转子平均风摩损耗并进行了多项式拟合，同时采用CFD法通过流固耦合场数值求解了端面对流换热热阻，最终通过拟合曲线获得了优化的BSRM凸极转子封盖尺寸，分析了相应的凸极转子性能。

1 计算流体动力学原理

目前，随着计算机数值计算性能大幅提升，CFD法已广泛应用于空气动力学分析、冷却系统仿真等各类流体流场分析及耦合场计算，特别是对复杂几何外型的腔体内流或壁面外流问题进行分析，相比于理论解析模型具有更高精度。有鉴于此，本文选用CFD软件ANSYS CFX对BSRM凸极转子外侧气隙流场分析，研究降低风摩损耗的凸极转子封盖优化设计方法。ANSYS CFX利用流体的一系列控制方程描述流场物理守恒定律，其中流体的连续性方程为[9]：

(1)

式中，ρ为流体密度，v为x、y、z三个方向流场速度矢量。流场的纳维—斯托克斯(navier-stokes，NS)方程为[9]：

(2)

式中，p为流场静压力，τ为流体应力张量，SM为额外冲量源，⊗为矢量张量积，NS方程描述了流场中流体动量守恒性质。而流场能量守恒方程为[9]：

(3)

式中，htot为总焓，ktc为流体导热率，·(v·τ)代表粘性应力做功，v·SM为外部冲量源做功，SE为外部能量源。对于湍流问题，特别是雷诺数较高时，湍流状态变化时间尺度小，采用直接数值模拟(direct numerical simulation，DNS)需要大幅降低计算步长，从而显著增加计算量。所以CFD法中通常采用时间平均化后的控制方程描述湍流状态，其中k-ε模型即为采用两方程描述的时间平均湍流模型，引入湍流动能k及湍流动能耗散率ε，首先由平均化的运输方程计算出相应的湍流动能和耗散率，再通过湍流动能求解湍流速度尺度，由湍流动能及其耗散率计算湍流长度尺度[9-10]。ANSYS CFX中提供了多种湍流模型，而k-ε模型中系数采用了大量流动实验验证，因而成为最广泛使用的湍流模型。ANSYS CFX基于上述控制方程采用有限体积法实现流场求解，首先通过网格划分将流场划分为有限多个控制体，其次将上式进行离散化并在各个控制体上进行数值求解，最终获得流场中特定点处各变量的近似数值解，整体的模型建立与求解流程图如图1所示[11]。首先依据定、转子几何尺寸，在CAD软件中建立气隙流场区域几何模型，由于CFD法相比于有限元法对网格质量要求更高，需要额外网格划分软件对流场区域进行网格处理，本文选用ANSYS自带的网格划分软件ANSYS ICEM人工划分了流场结构化网格，再将模型网格文件导入ANSYS CFX中，进行预处理，包括配置材料属性、设置转子转速、定义求解域、边界条件、湍流模型等参数，进而通过ANSYS CFX求解器进行流场数值求解，最终利用后处理模块分析流场求解结果。

图1 ANSYS CFX流场求解流程图Fig.1 Flow chart of solving the fluid field for ANSYS CFX

2 封盖尺寸对BSRM凸极转子风摩转矩影响分析

2.1 不同封盖尺寸转子端部空气流场网格划分

为在降低风摩损耗的同时提高转子对流换热性能，文献[8]提出了局部封闭的BSRM凸极转子结构，其封盖尺寸如图2所示[8]，相应的细节尺寸及性能参数参见文献[8]。然而所选取的30 mm封盖并非最优尺寸，本文在前文研究基础上分析不同封盖尺寸对凸极转子风摩转矩影响情况，首先离散选取了五组不同尺寸封盖转子模型进行建模与求解，包括26 mm(无封盖)、28.22 mm、30 mm、32.22 mm、33.5 mm(完全封闭)，相应带封盖转子的端部空气流场网格如图3所示，可见随着封盖尺寸增大，划分网格的端部空气区域越来越小，对于完全封闭的转子而言，在端部仅存在定、转子间狭窄气隙，对于气隙空气与机壳腔体内空气对流是不利的。

图2 局部封闭的凸极转子尺寸Fig.2 Dimension of rotor with partially covered shrouds

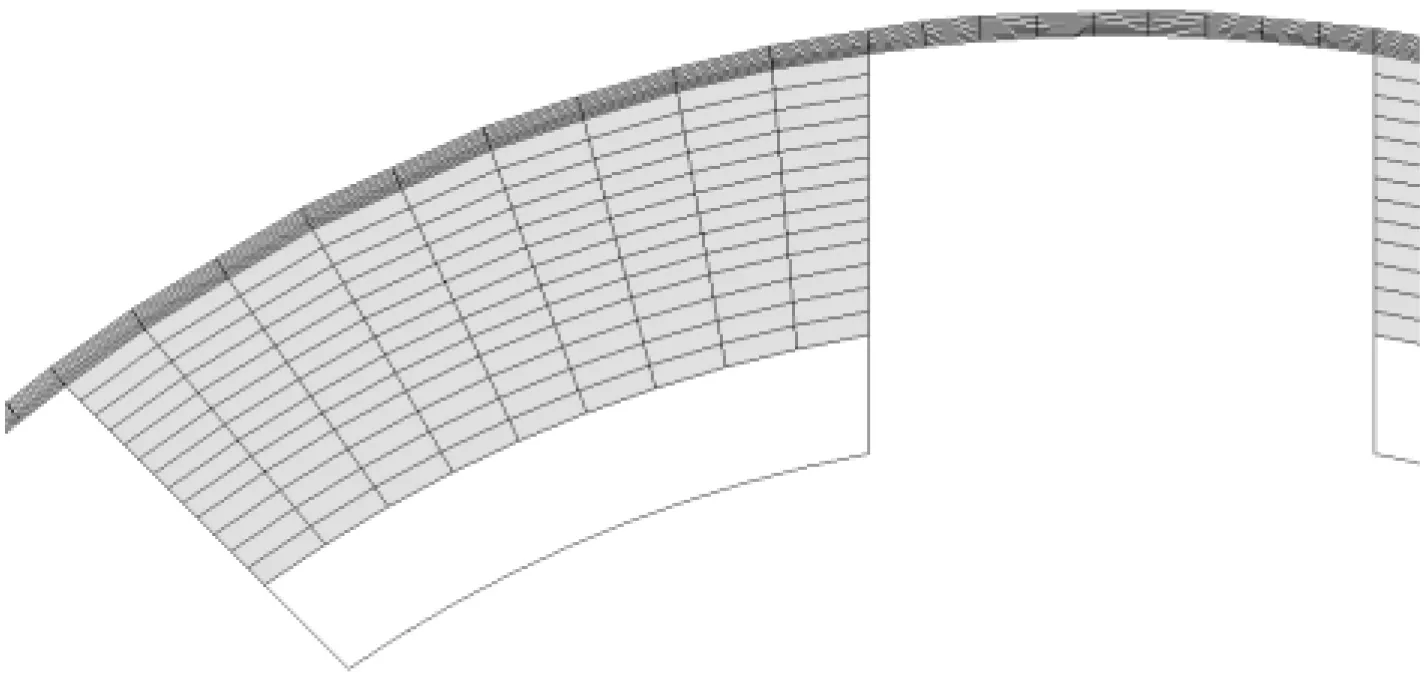
(a) 28.22 mm

(b) 30mm

(c) 32.22mm

(d) 33.5mm

图3 不同封盖尺寸转子端部空气流场网格
Fig.3 Mesh of the fluid field at the end of the rotor with different dimension of shroud

2.2 不同封盖尺寸转子端部空气流场分析

针对不同封盖尺寸凸极转子，采用CFD法对不同封盖尺寸转子在60 000 r/min转速下气隙流场求解，计算所得不同封盖尺寸转子3D流场速度矢量图如图4所示。可见随着封盖尺寸增大，转子端部湍流程度逐渐降低，有利于抑制风摩损耗[8]，而转子端部分布的高速度矢量逐渐减少，相应的空气对流逐渐减弱。同时通过CFD法计算了相应的平均风摩转矩，并采用三次多项式进行了拟合，拟合结果如图5所示，拟合的决定系数R2值为0.998，表明拟合精度较高，可见随着封盖尺寸增大转子风摩转矩逐渐降低，但当封盖直径超过30 mm后风摩转矩变化基本不大，且在32 mm尺寸附近存在局部峰值点，在封盖尺寸优化设计中，即采用拟合模型估算其风摩转矩。

(a) 28.22 mm

(b) 30 mm

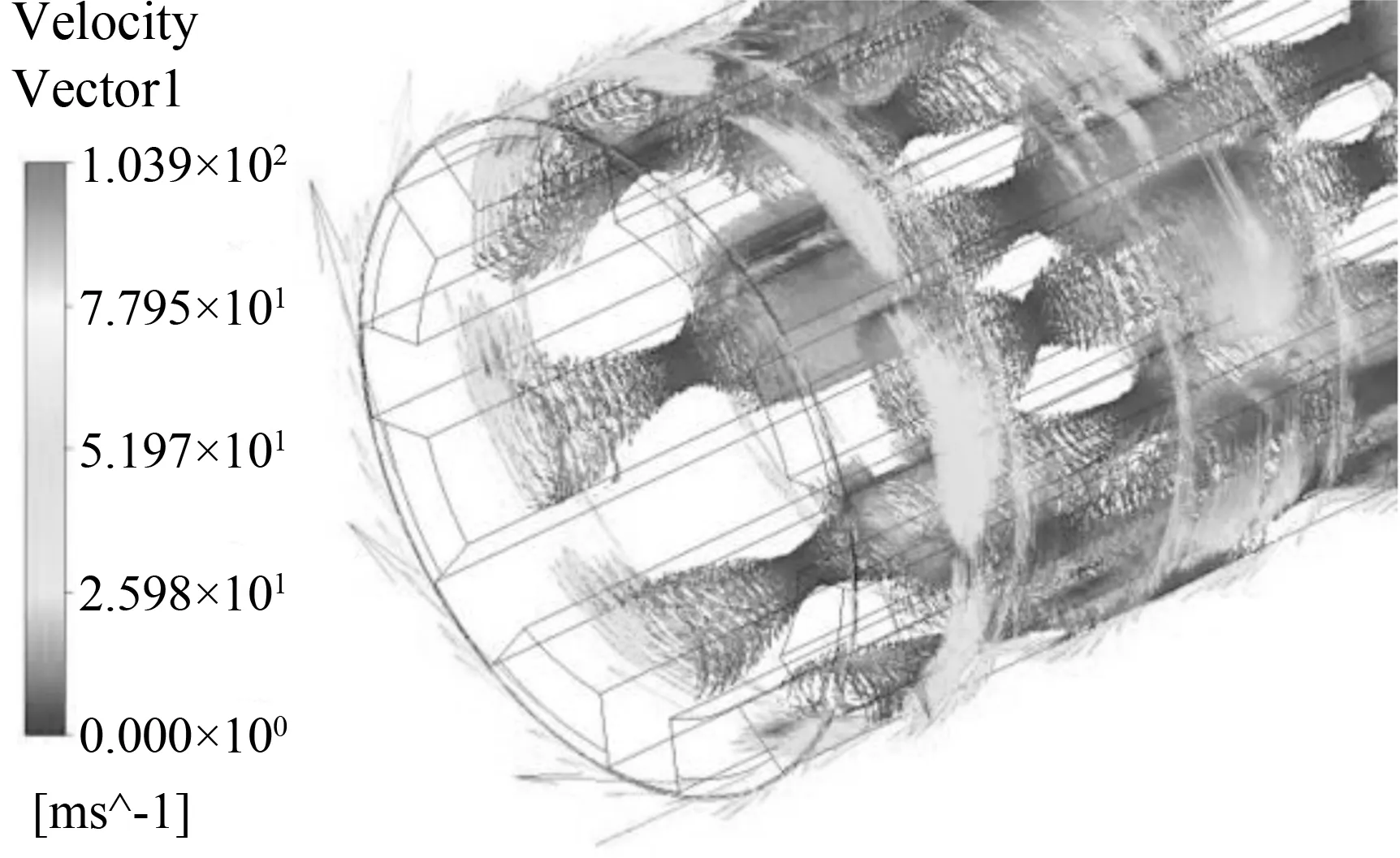
(c) 32.22 mm

(d) 33.5 mm

图4 不同封盖尺寸转子3D流场速度矢量图
Fig.4 3D fluid velocity vectors for the rotor with different dimension of shroud

图5 不同封盖尺寸转子风摩转矩及拟合结果Fig.5 Fitting result of windage loss of the rotor with different dimension of shroud

3 不同BSRM封盖尺寸对凸极转子对流热阻影响

为量化不同封盖尺寸凸极转子的气隙空气与机壳腔体内空气对流换热性能，本文采用转子端部对流热阻Rcov作为指标，其定义为：

(4)

式中，hcov为转子端面平均对流换热系数，Aside为端面对流换热面积。可见转子端面平均对流换热系数与端面对流换热面积越大，转子端部对流热阻Rcov越小，其散热性能越优。本文基于CFD法，选取了多组不同封盖尺寸的模型进行流固耦合场计算，所求解的端面对流换热热阻及相应的多项式拟合曲线如图6所示，拟合的决定系数R2值为0.987，随着转子封盖直径增大，端面对流换热热阻增大，散热性能越差，但在封盖直径30 mm附近存在局部极小值点。

图6 不同封盖尺寸转子端面对流换热热阻及拟合结果Fig.6 Fitting result of convection thermal resistance of the rotor with different dimension of shroud

4 局部封闭BSRM凸极转子封盖尺寸优化设计结果

基于转子封盖直径与其风摩转矩拟合模型、封盖直径与端面对流换热热阻拟合模型，建立了最终的封盖尺寸优化设计解集，相应的风摩转矩与对流换热热阻曲线如图7所示。选取了解空间中风摩转矩最小和端部对流换热热阻最小值点为理想解，并计算解集中各点到理想解的欧氏距离[12]，以欧氏距离最小值点对应的封盖尺寸30.88 mm为最终的优化封盖尺寸。表1对比了最终优化封盖与相邻尺寸封盖的转子性能，可见带有最终优化封盖的转子风摩转矩更接近31 mm封盖转子风摩转矩，而其端部对流热阻更接近30 mm封盖转子对流热阻，因此最终优化封盖尺寸实现了降低风摩转矩与端部对流热阻的折衷，在降低风摩损耗的同时提高了空气对流换热性能。

图7 风摩转矩与对流换热热阻曲线Fig.7 Curve of the convection thermal resistance relative to windage torque

表1 最终优化封盖与相邻尺寸封盖的转子性能对比Tab.1 Performance comparison between final optimization and the rotor with close dimension of shrouds

5 结论

为实现BSRM凸极转子风摩损耗抑制并改善转子对流换热性能，划分了不同封盖尺寸的凸极转子网格，采用CFD法求解了相应的3D气隙流场，计算了平均风摩转矩及端面对流换热热阻，通过拟合曲线获得了优化的BSRM凸极转子封盖尺寸。优化后的BSRM凸极转子封盖实现了降低风摩转矩与端部对流热阻的折衷，在降低风摩损耗的同时提高了空气对流换热性能。