不同温度下硅橡胶蠕变行为及变温黏弹性参数模型的建立

刘会英，李微微

(哈尔滨工业大学(威海)机械工程系，威海 264209)

0 引 言

胶辊是取款机、印刷机及工业设备中的重要部件，一般由金属辊芯和橡胶外层组成。硅橡胶由于具有耐高低温和耐磨耗的优点而广泛用作胶辊橡胶层材料。硅橡胶是一种黏弹性材料，兼具弹性固体及黏性流体的性质[1]，其黏弹性力学行为对胶辊的使用性能具有重要影响。蠕变特性是表征材料黏弹特性的重要指标之一，与环境温度、载荷及加载频率等因素密切相关[2]。近年来，国内外学者对黏弹性材料的蠕变行为开展了一系列研究。WILLIAMS等[3]认为升温与延长试验时间对分析材料的黏弹性具有等效性，并利用自由体积理论建立了表征时间-温度等效特性的WLF方程。ZACHARATOS等[4]以三参数固体模型为基础，推导出能够表征聚合物黏弹行为的一维唯象本构模型，并通过蠕变和松弛试验证明了模型的准确性。ARABANI等[5]利用Burgers模型研究了沥青混合料的黏弹特性，结果表明Burgers模型能够较好地表征该材料前期的蠕变行为。林松等[6]基于时间-应力等效原理研究了丁腈橡胶在不同温度及载荷下的蠕变行为，得到了参考应力下的蠕变柔量主曲线。张美美[7]利用标准线性固体模型对硅橡胶及丁腈橡胶蠕变试验结果进行了非线性拟合，得到了其在常温下的黏弹参数，但没有分析温度对材料黏弹参数的影响规律。魏轩等[8]研究了聚氨酯泡沫在常温下的蠕变特性，并利用Burgers模型对其蠕变行为进行了描述。黄传辉等[9]推导了一种双弹簧、双活塞黏弹性模型，并在常温状态针对尼龙PA66、聚四氟乙烯等材料进行了蠕变和松弛试验，发现该模型能有效反映聚合物的蠕变与松弛行为。李云良等[10]进行了水泥沥青复合胶结料(CACB)的蠕变试验，并以四元件五参数模型为基础，建立了CACB材料的黏弹性本构方程。

然而目前，关于材料黏弹性的研究大多集中于常温状态，仅有少数学者分析了温度对材料黏弹性的影响，但未明确黏弹性参数与温度间的函数关系。为此，作者以硅橡胶为研究对象，在不同温度下对其进行了蠕变试验，并基于三参数固体模型和无量纲分析方法建立了硅橡胶黏弹性参数预测模型，以期为硅橡胶及其他黏弹性材料的蠕变行为研究提供一定的参考。

1 表征蠕变行为的黏弹性本构模型

1.1 三参数固体模型

三参数固体模型由Maxwell模型与单弹簧模型并联而成，其结构如图1所示。

图1 三参数固体模型Fig.1 Three-parameter solid model

三参数固体模型的蠕变应变由弹簧瞬时弹性应变和阻尼牛顿黏性流动应变组成，其本构模型可表示为

(1)

在恒定应力σ0作用下，材料发生蠕变，其蠕变应变可表示为

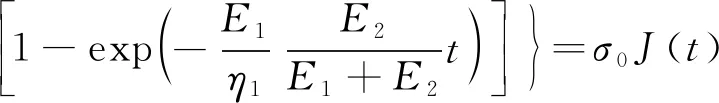
(2)

式中：J(t)为蠕变柔量；t为蠕变时间。

由式(2)可知，当t=0或t=∞时，材料的静态蠕变应变均为常数，说明三参数固体模型理论上能够准确描述橡胶的蠕变行为。

1.2 Burgers模型

Burgers模型由Maxwell模型和Kelvin模型串联而成，其结构如图2所示。

图2 Burgers模型Fig.2 Burgers model

Burgers模型的蠕变应变由弹簧瞬时弹性应变、Kelvin延迟弹性应变及阻尼牛顿黏性流动应变组成，其本构模型可表示为

(3)

在恒定应力σ0作用下，材料蠕变应变可表示为

σ0J(t)

(4)

由式(4)可知：当t=0时，静态蠕变应变为常数；t=∞时，蠕变应变趋于无穷大。这说明Burgers模型理论上无法准确描述静态蠕变行为。

2 变温蠕变试验

2.1 蠕变平台搭建及试验

试验用硅橡胶由安徽泰坤刷业有限公司提供，其室温邵氏硬度为57 HA。利用自制的静态蠕变试验装置(见图3)进行蠕变性能测试，蠕变试样尺寸为φ32 mm×12.5 mm，加载力为42 N，试验温度分别为-20，-5，10，25，40 ℃，通过高低温箱进行温度控制。

图5 不同温度下硅橡胶蠕变曲线拟合结果Fig.5 Fitting results of creep curves of silicone rubber at different temperatures

图3 蠕变试验装置示意Fig.3 Diagram of creep test device

以Labview编程语言为上位机搭建蠕变数据采集系统，使用位移传感器对试样变形量进行检测，所采集的数据经程序处理后直接转化为蠕变应变并自动存储至指定文件。

2.2 蠕变试验结果

由图4可知：随着时间的延长，不同温度下硅橡胶均发生了蠕变，且温度越高，蠕变速率越快，越先达到蠕变稳定期；当温度为-20，-5 ℃时，硅橡胶的蠕变应变范围较小、蠕变速率较慢。由此可见，硅橡胶的黏弹性与环境温度具有明显的相关性。

图4 不同温度下硅橡胶的蠕变曲线Fig.4 Creep curves of silicone rubber at different temperatures

2.3 黏弹性模型参数识别

利用Origin软件，基于Burgers模型和三参数固体模型分别对硅橡胶变温蠕变试验结果进行非线性拟合，结果如图5所示。计算得到两模型在不同试验温度下的黏弹性参数，见表1。由图5和表1可知：随着试验温度升高，两种模型的拟合精度均有所降低；当温度较高时，随蠕变时间的延长，Burgers模型蠕变应变近似成线性增大，蠕变应变趋于无穷大，与实际蠕变行为不符；而三参数固体模型的蠕变应变随时间延长慢慢趋于稳定，与试验结果吻合性好，能够比较准确地描述硅橡胶的非线性蠕变行为。因此，作者选择三参数固体模型来描述胶辊橡胶层材料的黏弹特性，并系统研究了黏弹性参数与温度之间的关系。

3 黏弹性参数预测模型的建立

3.1 无量纲模型参数拟合

假定无量纲黏弹性参数Y/Y′与无量纲温度θ/θ′符合多项式关系，即

(5)

表1 不同温度下两模型拟合得到的硅橡胶黏弹性参数及相关系数Table 1 Viscoelastic parameters and correlation coefficients of silicone rubber obtained by two models at different temperatures

式中：Y为三参数固体模型在温度θ下各黏弹性参数的值；θ′为参考温度，取40 ℃；Y′为参考温度θ′下各黏弹性参数的值；a0，a1，…，an分别为各阶多项式系数。

若假定Y/Y′与θ/θ′符合指数关系，即

(6)

采用无量纲分析方式对表1中三参数固体模型拟合得到的黏弹性参数进行处理，40 ℃为参考温度，结果见表2。通过Origin软件，分别采用式(5)和式(6)对表2中的数据进行拟合，得到硅橡胶无量纲黏弹性参数与无量纲温度的关系曲线，见图6，拟合系数见表3。由图6可知：硅橡胶的无量纲黏弹参数与无量纲温度之间亦具有明显相关性；三次多项式插值拟合函数的精度较指数函数的更高。

表2 不同温度下硅橡胶的无量纲黏弹性参数Table 2 Dimensionless viscoelastic parameters of silicone rubber at different temperatures

图6 硅橡胶的无量纲黏弹性参数-无量纲温度关系曲线Fig.6 Dimensionless viscoelastic parameter vs dimensionless temperature curves of silicone rubber: (a) curves of E2/2 vs θ/θ′;(b) curves of E1/1 vs θ/θ′ and (c) curves of η1/1vs θ/θ′

表3 不同拟合方式下硅橡胶无量纲黏弹性参数与无量纲温度函数的系数
Table 3 Function coefficients between dimensionless viscoelastic parameter and dimensionless temperature of silicone rubber under different fitting methods

拟合函数黏弹性参数a0a1a2a3R2拟合函数黏弹性参数a0a1a2a3R2E21.521-1.2831.325-0.5560.991E21.6960.7250.919式(5)E11.456-0.9180.646-0.1850.995式(6)E11.5430.5450.953η13.567-6.7424.911-0.7490.998η13.5561.6890.994

选择三次多项式插值拟合函数作为胶辊硅橡胶黏弹性参数与温度之间的函数关系式，建立的无量纲黏弹性参数预测模型为

3.2 参数方程验证

根据式(7)～(9)预测硅橡胶在任意温度下三参数固体模型的黏弹性参数，再将黏弹性参数代入式(2)中，预测得到硅橡胶在不同温度下的蠕变曲线。

由图7可知，蠕变曲线预测结果与试验结果吻合较好，说明建立的黏弹参数预测模型能够较为准确地预测硅橡胶材料在不同温度下的黏弹性参数。

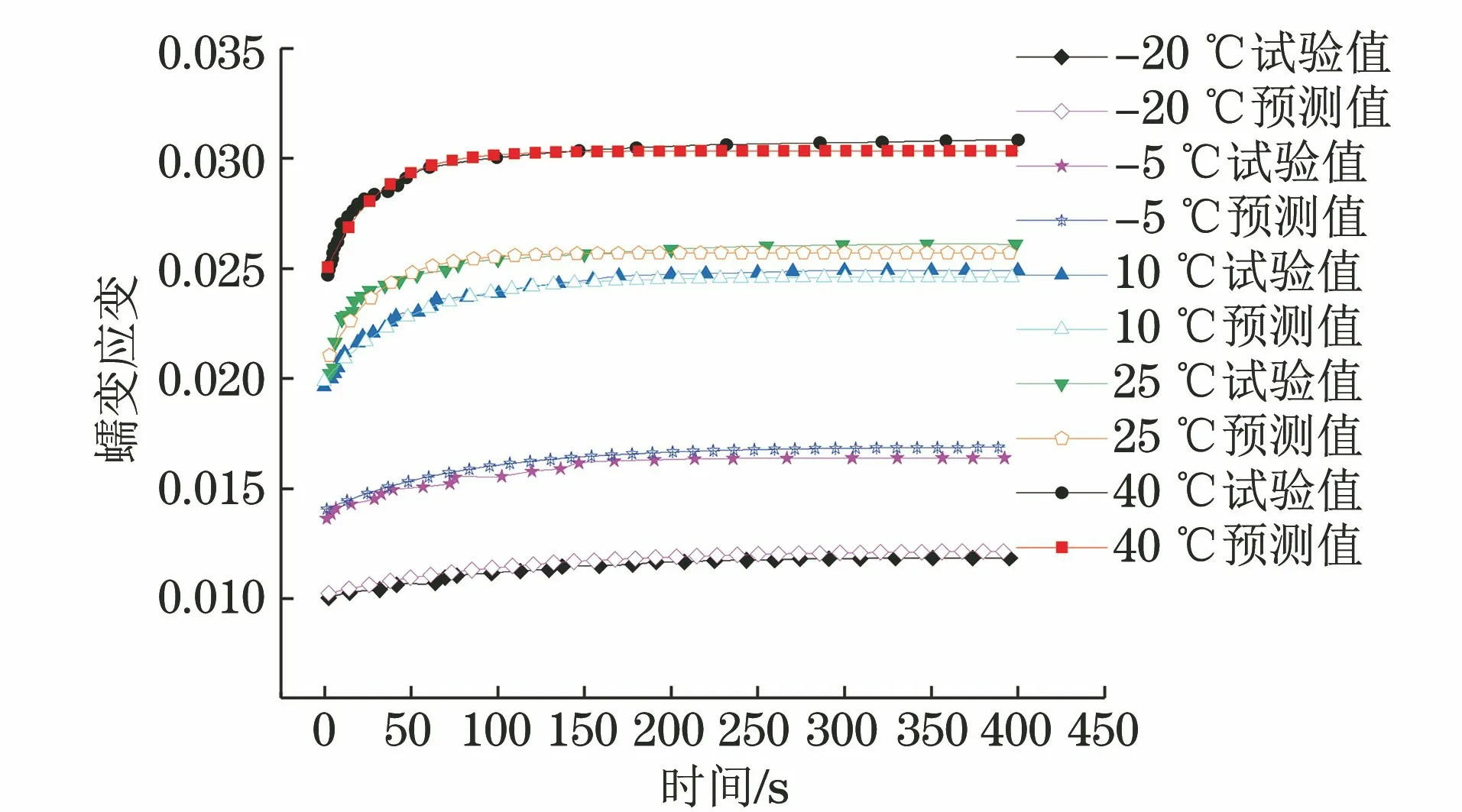
图7 硅橡胶蠕变曲线试验结果与黏弹参数模型预测结果Fig.7 Test results of creep curve of silicone rubber and prediction results of viscoelastic parameter model

4 结 论

(1) 硅橡胶的蠕变行为与温度具有明显的相关性，温度越高，硅橡胶蠕变应变和蠕变速率越大，蠕变应变越先达到稳定。

(2) 与Burgers模型相比，三参数固体模型能更准确地描述硅橡胶在不同温度下的静态蠕变特性。

(3) 基于三参数固体模型和无量纲分析方法建立的变温黏弹性参数预测模型能够预测硅橡胶材料在任意温度下的蠕变应变，预测结果与试验结果吻合较好，预测精度较高。