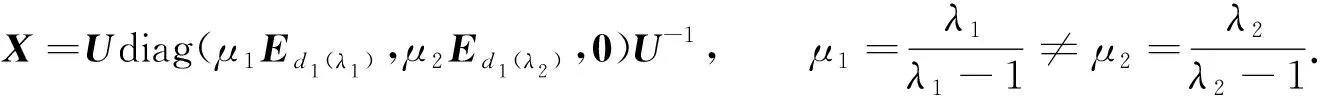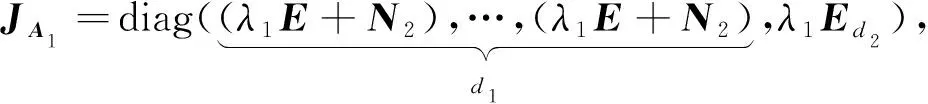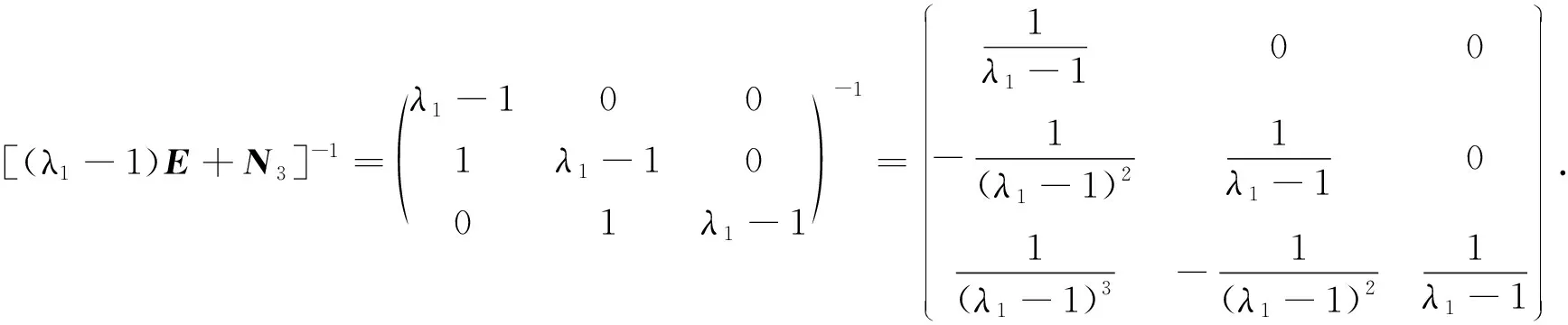矩阵方程A+X=AX广义三次矩阵解与绝对值方程的解

吕洪斌, 杨忠鹏, 陈梅香, 王信存

(1.北华大学 数学与统计学院, 吉林 吉林 132013； 2.莆田学院 数学与金融学院, 福建 莆田 351100；3.辽东学院 师范学院, 辽宁 丹东 118003)

0 引 言

文献[1]给出广义三次矩阵的定义： 对给定矩阵P=P2, 若A∈n×n满足

A3=αA2+βA+γP,PA=AP=A,α,β,γ∈,

则称A为(由α,β,γ确定的)广义三次矩阵.对给定矩阵P=P2, 记

Ωn(P;α,β,γ)={A∈n×n|A3=αA2+βA+γP,AP=PA=A}.

(1)

设A,B∈n×n, 如果AB=A+B, 则称A,B为和与积相等的矩阵对, 而关于该类矩阵的研究目前已有很多结果[2-5].文献[6]研究了矩阵方程AX=A+X, 得到了方程有正定解和幂零解的充要条件; 文献[7]给出了广义三次矩阵的Jordan标准形.本文应用广义三次矩阵的Jordan标准形, 给出矩阵方程AX=A+X有广义三次矩阵解的充要条件及解的形式, 并证明了由AX=A+X的广义三次矩阵解B所确定的绝对值方程Bx-|x|=b(B∈n×n,b∈n)有解x∈n.

1 预备知识

引理1[7]设P=P2给定,A∈n×n且AP=PA=A, 则有可逆矩阵G, 使得

P=Gdiag(Er,0)G-1,r(P)=r;A=Gdiag(A1,0)G-1,A1∈r×r;

(2)

引理2[7]设s(x)=x3-αx2-βx-γ∈[x]给定, 如果x1,x2,x3是x3+px+q∈[x]的所有根, 其中则为s(x)的所有根, 且

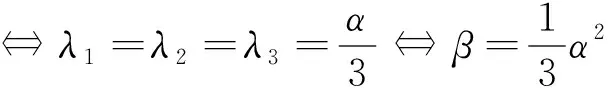
(3)

显然有:

引理3设A∈n×n, 则矩阵方程A+X=AX有解⟺矩阵A-E可逆, 即1不是A的特征值.当A-E可逆时, 矩阵方程A+X=AX有唯一解X=E+(A-E)-1.

引理4[6]设A∈n×n,X为矩阵方程A+X=AX的解, 则AX=XA.

引理5设P=P2给定,A∈n×n且AP=PA=A.如果X为矩阵方程A+X=AX的解, 则PX=XP=X.

证明： 应用引理4, 有

XP=(AX-A)P=(XA-A)P=XA-A=AX-A=X,

PX=P(AX-A)=AX-A=X,

即结论成立.证毕.

的所有根.

证明： 由λi≠1知μi≠1(i=1,2,3),s(1)=1-α-β-γ≠0.令

h(x)=(x-μ1)(x-μ2)(x-μ3)=x3-ax2-bx-c,

于是由多项式方程根与系数的关系易得

证毕.

引理7[8]设P=P2∈n×n给定,A∈n×n.如果A∈Ωn(P;α,β,γ),γ(≠0),α,β∈且绝对值方程P|x|=|x|无非零解, 则绝对值方程Ax-|x|=b(b∈n)有解(x∈n).

2 广义三次矩阵的Jordan标准形

定理1[7]设P=P2给定, 在引理2的条件下, 有：

1) 若A∈Ωn(P;α,β,γ)由式(1)确定, 则

A3-αA2-βA-γP=(A-λ1P)(A-λ2P)(A-λ3P),

(4)

2) 如果A∈n×n,AP=PA=A且式(2)成立, 则

A3-αA2-βA-γP=0⟺ (A1-λ1Er)(A1-λ2Er)(A1-λ3Er)=0.

定理2[7]设P=P2给定,A∈Ωn(P;α,β,γ) , 在引理2的条件及式(2)情形下, 则A1∈r×r的Jordan标准形如下：

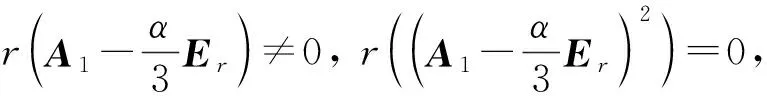
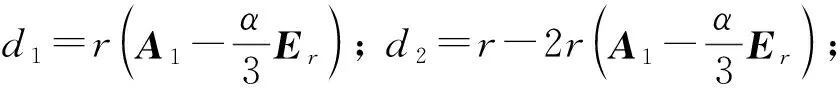
这里:

① 如果r(A1-λ1Er)=0, 则JA1=A1=λ1Er;

② 如果r(A1-λ2Er)=0, 则JA1=A1=λ2Er;

③ 如果0

0

则

JA1=diag(λ1Ed1(λ1),λ2Ed1(λ2))；

④ 如果r(A1-λ1Er)=r, 0

这里d2(λ2)=r-2r(A1-λ2Er)；

⑤ 如果0

这里:

d1(λ2)=r(A1-λ1Er)+r(A1-λ2Er)-r;

d2(λ2)=2r-r(A1-λ1Er)-2r(A1-λ2Er).

3) 当(α2+4β)β2≠(4α3+27γ+18αβ)γ时, 如果0

JA1=diag(λ1Ed1(λ1),λ2Ed1(λ2),λ3Ed1(λ3)).

定理3[7]设P=P2给定,A∈Ωn(P;α,β,γ), 则存在可逆矩阵U, 使得

U-1PU=diag(Er,0),U-1AU=JA=diag(JA1,0),

(6)

其中JA1由定理2确定.

3 主要结果

由于下面讨论涉及到不止一个广义三次矩阵, 所以记A∈Ωn(P;αA,βA,γA).

定理4设P=P2∈n×n给定,A∈n×n, 则矩阵方程A+X=AX有解X∈Ωn(P;αX,βX,γX)且1不是X的特征值⟺A∈Ωn(P;αA,βA,γA)且1不是A的特征值, 且有

(7)

(8)

证明： 当A∈Ωn(P;αA,βA,γA)时, 由定理2和定理3知JA1可分为下列三种情形:

情形1) 对定理2中1)的①及2)的①②情形, 有JA1=A1=λiEr(i=1,2,3), 再由式(6)有

A=UJAU-1=Udiag(JA1,0)U-1=λiUdiag(Er,0)U-1=λiP,i=1,2,3.

(9)

由式(9)知此时式(4)成立.又由引理3知λi≠1且A-E可逆, 应用式(6)和(9), 有

即

(10)

由引理3和引理4知PX=XP=X, 再由式(10)得

(X-μ1P)(X-μ2P)(X-μ3P)=0,

于是由式(4),(5)和引理6知

X∈Ωn(P;αX,-βX,γX)=Ωn(P;μ1,μ2,μ3),

(11)

且式(7)成立.

情形2) 当JA1可对角化且非数量幂等时, 有定理2中2)的③和3)两种情形:

① 对定理2中2)的③情形, 有JA1=diag(λ1Ed1(λ1),λ2Ed1(λ2)),λ1≠λ2, 应用式(6)有

A=UJAU-1=Udiag(JA1,0)U-1=Udiag(λ1Ed1(λ1),λ2Ed1(λ2),0)U-1.

(12)

由式(12)知此时式(4)成立, 由引理3及式(6),(12), 有

即

(13)

由引理3和引理4知PX=XP=X, 进而由式(6),(13)得

于是由式(4),(5)和引理6知式(11)成立.

② 对定理2中3)的情形,JA1=diag(λ1Ed1(λ1),λ2Ed1(λ2),λ3Ed1(λ3)),λ1,λ2,λ3两两不同, 应用式(6)有

A=UJAU-1=Udiag(JA1,0)U-1=Udiag(λ1Ed1(λ1),λ2Ed1(λ2),λ3Ed1(λ3),0)U-1.

(14)

由式(14)知此时式(4)成立, 由引理3和式(6),(14), 有

即

X=Udiag(μ1Ed1(λ1),μ2Ed1(λ2),μ3Ed1(λ3),0)U-1,

(15)

由引理3和引理4知PX=XP=X, 进而由式(6),(15), 有

于是由式(4),(5)和引理6知式(11)成立.

情形3) 当JA1不可对角化时, 有定理2中1)的②③和2)的④⑤共4种情形：

① 对定理2中1)的②情形,

由式(6)有

(16)

(17)

由式(16)知此时式(4)成立, 由式(6),(16),(17)和引理3, 有

于是

(18)

由定理2中1)的②证明知, 此时λ1=λ2, 故μ1=μ2.又由引理3和引理4知PX=XP=X, 进而由式(6),(18), 有

于是由式(4),(5)和引理6知式(11)成立.

② 对定理2中1)的③情形,

应用式(6)有

(19)

(20)

由式(19)知此时式(4)成立, 由引理3和式(6),(19),(20), 有

于是,

(21)

由定理2中1)的③证明知, 此时λ1=λ2=λ3, 故μ1=μ2=μ3.由引理3和引理4知

PX=XP=X,

从而由式(6),(21), 有

于是由式(4),(5)和引理6知式(11)成立.

③ 对定理2中2)的情形④,

由3)中①知此时λ1=λ2, 因此只要将3)中①的λ1对应用λ2置换即可知式(11)成立.

④ 对定理2中2)的情形④,

应用式(6)有

(22)

即

(23)

由定理2中2)的⑤证明知λ1≠λ2=λ3, 故μ1≠μ2=μ3.又由引理3和引理4知PX=XP=X, 从而由式(6),(23), 有

于是由式(4),(5)和引理6知式(11)成立.

当矩阵方程A+X=AX有解X∈Ωn(P;αX,βX,γX)且1不是X的特征值时, 由引理4知AX=XA即可将A视为X+A=XA(=AX=A+X)的解, 由上述讨论知A∈Ωn(P;αA,βA,γA)=Ωn(P;λ1,λ2,λ3),λi≠1(i=1,2,3)且式(8)成立.证毕.

推论1设P=P2∈n×n给定,A∈Ωn(P;αA,βA,γA), 1不是A的特征值且式(6)成立, 则A+X=AX有由幂等矩阵P确定的广义三次矩阵解X, 当时, 有：

1) 当A=λiP(i=1,2,3)时,X=μiP;

2) 当A=Udiag(λ1Ed1(λ1),λ2Ed1(λ2),0)U-1,λ1≠λ2时,X=Udiag(μ1Ed1(λ1),μ2Ed1(λ2),0)U-1;

3) 当A=Udiag(λ1Ed1(λ1),λ2Ed1(λ2),λ3Ed1(λ3),0)U-1,λ1,λ2,λ3两两不同时,

X=Udiag(μ1Ed1(λ1),μ2Ed1(λ2),μ3Ed1(λ3),0)U-1;

其中,d1(λ1),d1(λ2),d1(λ3),d2(λ2)由定理2中的相应结论确定.

证明: 由定理2和定理3及式(9),(12)～(17),(19),(21)～(23)可得相应解的表达式.证毕.

定理5设P=P2∈n×n给定, 1不是A∈n×n的特征值.如果A∈Ωn(P;αA,βA,γA)(αA,βA,γA∈), 则实矩阵方程A+X=AX有由幂等矩阵P确定的实广义三次矩阵解X∈Ωn(P;αX,βX,γX)(αX,βX,γX∈), 且1不是X的特征值.

证明: 由定理4及其证明知, 矩阵方程A+X=AX有由幂等矩阵P确定的广义三次矩阵解X∈Ωn(P;αX,βX,γX)且1不是X的特征值, 同时式(7)成立, 此时X=E+(A-E)-1.因为A∈n×n, 所以X=E+(A-E)-1∈n×n, 再注意到αA,βA,γA∈, 于是由式(7)知αX,βX,γX∈.证毕.

绝对值方程Ax-|x|=b是一个不可微的NP-难问题, 其研究主要源于区间线性方程[9-10]和线性互补问题[11-12].文献[8]用拓扑度理论给出了绝对值方程可解的充分条件, 并证明了当矩阵A为广义三次矩阵时, 绝对值方程不存在例外族, 从而绝对值方程有解.

定理6设P=P2∈n×n给定且绝对值方程P|x|=|x|(x∈n)无非零解, 1不是A∈n×n的特征值, 且A∈Ωn(P;αA,βA,γA),αA,βA,γA∈,γA≠0.如果B∈n×n是实矩阵方程A+X=AX的解, 则绝对值方程Bx-|x|=b(b∈n)有解(x∈n).

证明: 因为1不是A∈n×n的特征值, 且A∈Ωn(P;αA,βA,γA),αA,βA,γA∈, 由定理5知, 实矩阵方程A+X=AX有实矩阵解X∈Ωn(P;αX,βX,γX).由引理4知, 对于实矩阵方程A+X=AX也成立, 从而B=E+(A-E)-1=X∈Ωn(P;αX,βX,γX).又由式(7)及γA≠0得γX≠0.注意到此时绝对值方程P|x|=|x|(x∈n)无非零解, 于是应用引理7知, 绝对值方程Bx-|x|=b(b∈n)有解(x∈n).证毕.