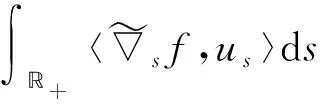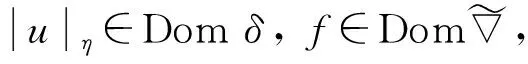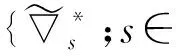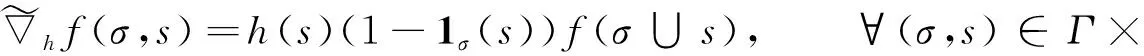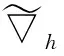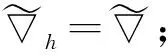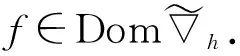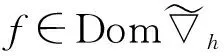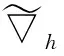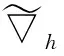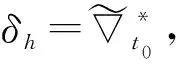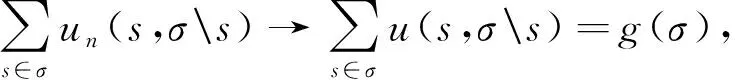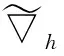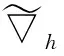广义修正随机梯度与广义Skorohod积分
周玉兰, 程秀强, 薛 蕊, 李晓慧
(西北师范大学 数学与统计学院, 兰州 730070)
1 预备知识
设η是复Hilbrt空间, 其上的内积、范数分别记作〈·,·〉η和|·|η.L2(Γ;η)是Γ上η值平方可积函数所成的Hilbert空间, 其上内积为
L2(Γ×+;η)是Γ×+上η值平方可积函数所构成的Hilbert空间, 其上内积为
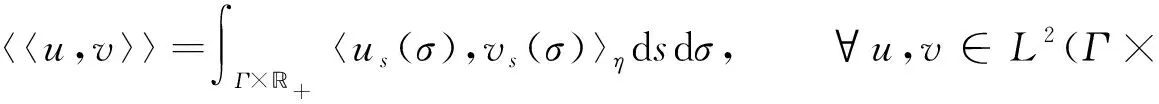
约定L2(Γ×+;η)上的范数为|‖·‖|,L2(Γ;η)上的范数为‖·‖.对∀s,t∈+及∀ω,σ,τ∈Γ, 约定: ∨σ∶=max{s:s∈σ}, ∧σ∶=min{s:s∈σ};σ-∶=σ{∨σ},σs∶=σ{s};ω∪s∶=ω∪{s},σ<τ⟺s (1) (2) 定义2[10]设u是Γ×+上η值过程, 定义Γ上函数为若δ(u)平方可积, 则称δ(u)为u的Skorohod积分.其定义域为 Domδ={x∈L2(Γ×+;η)|δ(x)∈L2(Γ;η)}. (3) 定义3[10]设u是Γ×+上的η值过程, 若u是可测的, 且Γ×+上的映射(σ,k)→|u(σ,k)|η是Skorohod可积的, 则称u是绝对Skorohod可积的. 注1δ是L2(Γ×+;η)中无界稠密的闭算子. 命题2[10]L2(Γ×+;η)中的Skorohod积分算子δ与L2(Γ;η)中的修正随机梯度算子是共轭的, 即 (4) (5) (6) 定义6设x是Γ×+上的η值过程, 若函数s‖xs(·)‖(s∈+,xs∈L2(Γ;η))是+上的可积函数, 则称x是Bochner可积的. (7) 存在, 且 (8) 式(8)成立.证毕. (9) (10) 存在, 且 (11) 即式(11)成立.证毕. (12) 定义7设h是+上的非负实函数, 在Γ上定义非负值函数为称#h(·)为Γ上的h计数. 定义8设h是+上的非负实函数, 定义算子+;η)如下: (13) 定理3设h是+上的非负函数, 则广义修正随机梯度是L2(Γ;η)中的稠定闭线性算子. 证明: 对∀k≥1, 记Ek={t;k-1≤h(t) Γ(n,k)=Γ(n)∩Ek={σ;#σ=n,s∈σ,k-1≤h(s) 对∀f∈L2(Γ(n,k);η),f(σ)=1Γ(n)(σ)1Ek(σ)f(σ), 有 则对∀(σ,s)∈Γ×+, 有fn(σ)→f(σ), 进而 h(s)(1-1σ(s))|fn(σ)-f(σ)|→0. 而|h(s)(1-1σ(s))f(σ∪s)-us(σ)|→0, 故us(σ)=h(s)(1-1σ(s))f(σ∪s), 且 定理4设h是+上非负实函数, 若则是L2(Γ;η)到L2(Γ×+;η)的有界线性算子, 且 定义9对+上的非负函数h, 定义算子δh:L2(Γ×+;η)→L2(Γ;η)如下: (14) 称δh为关于h的广义Skorohod积分, 其定义域为Domδh={u∈L2(Γ×+;η)|δ(hu)∈L2(Γ;η)}. 定理5设h是+上的非负函数, 则广义Skorohod积分δh是L2(Γ×+;η)中的稠定闭算子. 另一方面, 设{un}n≥1⊂Domδh,un→u(n→∞),δh(un)→g∈L2(Γ;η), 则 即u∈Domδh且g=δh(u), 故δh是闭的.证毕. 定理6若+上的非负函数h满足则Domδ⊂Domδh, 此时δh是L2(Γ×+;η)到L2(Γ;η)中的有界线性算子, 且 即u∈Domδh.由u的任意性,Domδ⊂Domδh.又由于Domδ是L2(Γ×+;η)中稠子集, 由式(15)及可将δh唯一地延拓为L2(Γ×+;η)到L2(Γ;η)中的有界线性算子, 且证毕. 定理7设h是+上的非负函数, 对积分 (16) (18)

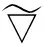
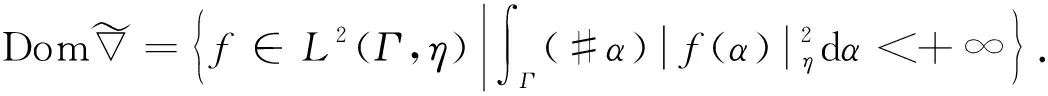



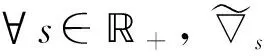
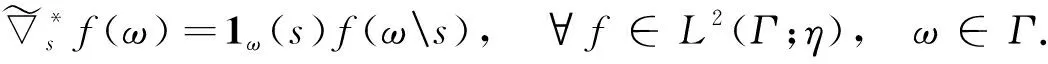
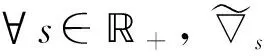
2 主要结果及证明