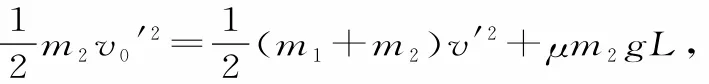动量守恒经典好题赏析
■湖南省汨罗市一中
一、建立柱状模型,应用动量定理解题
例1(2016年高考全国Ⅰ卷)某游乐园入口旁有一喷泉,喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中。为计算方便起见,假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出;玩具底部为平板(面积略大于S);水柱冲击到玩具底板后,在竖直方向上水的速度变为零,在水平方向上朝四周均匀散开。忽略空气阻力。已知水的密度为ρ,重力加速度大小为g。求:
(1)喷泉单位时间内喷出的水的质量。
(2)玩具在空中悬停时,其底面相对于喷口的高度。
解析
(1)在一段很短的时间Δt内,可认为喷出的水柱保持速度v0不变。这段时间内,喷出的水柱的高度Δl=v0·Δt,体积ΔV=Δl·S,质量Δm=ρ·ΔV,解得喷泉单位时间内喷出的水的质量为。
(2)由玩具受力平衡得F冲=Mg,其中F冲为水柱对玩具底面的作用力。由牛顿第三定律可知,玩具底面对水的反作用力F压=F冲。设玩具悬停时其底面相对于喷口的高度为h,水柱到达玩具底面时的速度为v′,由运动学公式得。在一段很短的时间Δt内,冲击玩具底面的水柱的质量Δm=ρv0SΔt。由题意可知,在竖直方向上,对这部分水柱应用动量定理得(F压+Δm·g)Δt=Δm·v′。因为Δt很小,所以Δm·g也很小,可以忽略,则F压·Δt=Δm·v′,解得。
小结:求解“连续”质点系统发生持续作用,物体动量(其他量)连续发生变化类问题的思路是先正确选取研究对象,即选取很短时间Δt内动量(其他量)发生变化的那部分物体作为研究对象;再建立“柱状模型”,即在时间Δt内所选取的研究对象均分布在以S为截面积、长为v·Δt的柱体内,这部分质点的质量Δm=ρSvΔt,以这部分质量的质点系统为研究对象,研究它在Δt时间内的动量(其他量)的变化情况;然后根据动量定理(其他物理规律)求出相关物理量。
现学现练:如图1所示,静止在光滑水平面上的小车质量M=20kg。从水枪中喷出的水柱的横截面积S=10cm2,速度v=10m/s,水的密度ρ=1×103kg/m3。若用水枪喷出的水从车后沿水平方向冲击小车的前壁,且冲击到小车前壁的水全部沿前壁流进小车中。当有质量m=5kg的水进入小车时,试求:
(1)小车的速度大小。
(2)小车的加速度大小。
答案:(1)2m/s;(2)2.56m/s2。
提示:(1)流进小车的水与小车组成的系统动量守恒,则mv=(M+m)v1,解得v1=2m/s。(2)质量为m的水流进小车后,在极短的时间Δt内,冲击小车的水的质量Δm=ρS(v-v1)Δt,设此时水对车的冲击力为F,则车对水的作用力为-F,由动量定理得-FΔt=Δmv1-Δmv,解得F=64N。由牛顿第二定律得F=(M+m)a,解得a=2.56m/s2。
二、经典碰撞,万变不离其宗
例2(2015年高考全国Ⅰ卷)如图2所示,在足够长的光滑水平面上,物体A、B、C位于同一直线上,物体A位于B、C之间。物体A的质量为m,物体B、C的质量都为M,三者均处于静止状态。现使物体A以某一速度向右运动,求m和M之间应满足什么条件,才能使物体A只与B、C各发生一次碰撞。设物体间的碰撞都是弹性碰撞。
现学现练:A、B两物体在光滑水平面上沿同一直线运动,图3表示两物体发生碰撞前后的v-t图像,由图像可以判断( )。
A.两物体的质量之比为3:2
B.两物体碰撞前后总动量守恒
C.两物体碰撞前后总动量不守恒
D.两物体碰撞前后总动能不变
答案:ABD
提示:两物体碰撞前的速度分别为vA=6 m/s,vB=1 m/s,碰撞后的速度分别为vA′=2 m/s,vB′=7 m/s。两物体碰撞前后动量守恒,根据动量守恒定律得mAvA+mBvB=mAvA′+mBvB′,解得mA:mB=3:2,选项A、B正确,C错误。两物体碰撞前的总动能为,碰撞后的总动能为,因此两物体碰撞前后总动能不变,选项D正确。
三、多运动过程问题的综合分析
例3(2015年高考广东卷)如图4所示,一条带有圆轨道的长轨道水平固定,圆轨道竖直,底端分别与两侧的直轨道相切,半径R=0.5m,物块A以速度v0=6m/s滑入圆轨道,滑过最高点Q,再沿圆轨道滑出后,与直轨道上P处静止的物块B碰撞,碰后两物块粘在一起运动,P点左侧轨道光滑,右侧轨道呈粗糙段、光滑段交替排列,每段长度都为L=0.1m,物块与各粗糙段间的动摩擦因数都为μ=0.1,A、B两物块的质量均为m=1kg(取重力加速度g=10 m/s2;A、B两物块可视为质点,碰撞时间极短)。
(1)求物块A滑过Q点时的速度大小v和受到的弹力大小F。
(2)若碰后A、B两物块最终停止在第k个粗糙段上,求k的数值。
(3)求碰后A、B两物块滑至第n个(n<k)光滑段上的速度vn与n的关系式。
解析
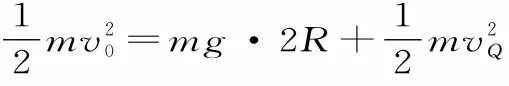

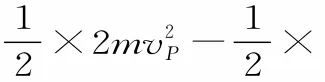
小结:应用力学三大观点解题时应注意以下四个问题。(1)弄清有几个物体参与运动,并划分清楚各物体的运动过程。(2)进行正确的受力分析,明确各运动过程的特点。(3)若物体在光滑的平面或曲面上运动,或物体参与不计阻力的抛体运动,则机械能一定守恒;若是碰撞过程、子弹打击木块情景,以及不受其他外力作用的两物体相互作用问题,则一般考虑用动量守恒定律求解。(4)若是含摩擦生热问题,则考虑用能量守恒定律求解。
现学现练:如图5所示,粗糙的水平面连接一个竖直平面内的光滑半圆形轨道,其半径R=0.1m,半圆形轨道的底端放置一个质量m=0.1kg的小球B,水平面上有一个质量M=0.3kg的小球A以初速度v0=4m/s向着小球B滑动,经过时间t=0.8s与小球B发生弹性碰撞。两小球均可以看成质点,碰撞时间极短,已知小球A与水平面间的动摩擦因数μ=0.25,取重力加速度g=10m/s2。求:
(1)两小球碰前小球A的速度。
(2)小球B运动到最高点C时对轨道的压力。
(3)小球A最终所停的位置到半圆形轨道最低点的距离。
答案:(1)2m/s;(2)大小为4N,方向竖直向上;(3)0.2m。
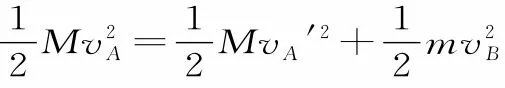
四、滑块—木板模型经典再现
例4如图6所示,在光滑的水平面上并排放着两个相同的木块,长度均为L=1 m,在左边木块的左端放一个小金属块,它的质量和一个木块的质量相等。现令金属块以初速度v0=2 m/s开始向右滑动,金属块与木块间的动摩擦因数μ=0.1。取重力加速度g=10m/s2,求右边木块的最后速度。
解析
若金属块最后停在左边的木块上,则两木块和金属块将以相同的速度运动。设三者最终的共同速度为v,金属块最后距左边木块左端的距离为x,则0<x≤L。由动量守恒定律得mv0=3mv,由能量守恒定律得解得,说明金属块最后不能停在左边的木块上。设金属块最后停在右边的木块上距离左端为x处,则0<x≤L。设两木块最终的速度分别为v1、v2(v1<v2),金属块到达左边木块右端时的速度为v0′,由动量守恒定律得mv0=mv0′+2mv1,mv0=mv1+2mv2,由能量守恒定律得,说明金属块最后停在右边的木块上,且右边木块的最后速度。
小结:滑块—木板模型可分为两类,即单一滑块模型和多个滑块模型。求解单一滑块模型问题主要运用牛顿第二定律、动能定理或动量定理等进行分析。求解多个滑块模型问题应着重分析物体的运动过程,明确它们之间的时间、空间关系,并注意临界、隐含和极值等条件,运用动量守恒定律、机械能守恒定律或能量守恒定律等进行分析。
现学现练:如图7所示,质量m1=0.3kg的小车静止在光滑的水平面上,车长L=15m,现有质量m2=0.2kg的物块(可视为质点),以水平向右的初速度v0=2 m/s从左端滑上小车,最后在车面上某处与小车保持相对静止。已知物块与车面间的动摩擦因数μ=0.5,取重力加速度g=10m/s2。
(1)求物块在车面上滑行的时间t。
(2)要使物块不从小车右端滑出,物块滑上小车左端的初速度v0′不超过多少?
答 案:(1)t=0.24 s;(2)。