圆周运动问题的求解策略
■河南省平顶山市第一中学
圆周运动包含水平面内的匀速圆周运动和竖直面内的变速圆周运动两类模型,求解圆周运动问题不仅需要熟练掌握圆周运动相关概念、规律和公式,还需要灵活选用解题技巧和方法。下面举例分析。
一、水平面内圆周运动问题的求解策略
1.明确运动形式:研究对象在水平面内沿圆周做速度大小不变的运动。
2.确定向心力来源:向心力是按力的作用效果命名的,可以是重力、弹力、摩擦力等各种力,也可以是几个力的合力或某个力的分力。在匀速圆周运动中,向心力是由物体受到的合外力来提供的,它只能改变速度的方向,不能改变速度的大小。向心力是变力,其大小。
3.正确进行受力分析:沿半径方向和垂直于半径方向将研究对象受到的各力进行分解,根据牛顿第二定律和向心力公式列方程。
4.合理选择过程分析:根据题意选择满足动能定理或机械能守恒定律的运动过程,应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程求解。
例1如图1甲所示,一质量为m的小球系在两根不可伸长的轻绳a、b一端,两轻绳的另一端拴接在竖直杆上的A、B两点上。当两轻绳伸直时,轻绳a与竖直杆间的夹角θ=30°,轻绳b水平,如图1乙所示。已知轻绳a的长度为2L。竖直杆以自己为轴转动,在其角速度ω从零开始缓慢增大的过程中(不同ω对应的轨迹可看成是稳定的圆周运动轨迹),下列说法正确的是( )。
A.从开始至轻绳b伸直但不提供拉力时,轻绳a对小球做的功为0
B.从开始至轻绳b伸直但不提供拉力时,小球的动能增加了
C.从开始至轻绳b伸直但不提供拉力时,轻绳a对小球做的功为
答案:BC
点评:从开始至轻绳b伸直但不提供拉力,轻绳a对小球要做功。因为圆周运动的轨迹发生变化,轻绳a的拉力为变力,所以可以先根据牛顿第二定律和向心力公式求出轻绳b刚要伸直时小球的速度,再根据动能定理求得轻绳a对小球做的功。根据角速度与速度的关系分析轻绳b刚要伸直时小球的角速度,进而可判断出当时轻绳b是否伸直。
二、竖直面内圆周运动问题的求解策略
1.明确物理模型:判断是轻绳模型还是轻杆模型。
3.确定研究状态:在高中阶段研究的竖直平面内的圆周运动只涉及最高点和最低点的运动情况。
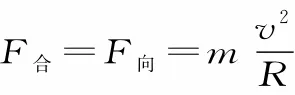
5.合理选择过程分析:根据题意选择满足动能定理或机械能守恒定律的运动过程,应用动能定理或机械能守恒定律将初、末两个状态联系起来列方程求解。
例2如图2所示,细线的一端系一质量为m的小球,以另一端O为圆心,使小球在竖直面内做半径为R的圆周运动。若小球在竖直向上方向上受到恒力F的作用,为使小球能做完整的圆周运动,在最低点B小球至少应有多大的初速度?
解析
小球在运动过程中,受到重力mg、拉力T和恒力F三个力的作用。根据重力mg和恒力F的大小关系分两种情况讨论。
(1)若F<mg,则物理上的最高点与几何上的最高点重合,为A点。设小球能通过A点的临界速度为vA,由牛顿第二定律和向心力公式得,解得。对小球从B点运动到A点的过程应用动能定理得。
(2)若F>mg,则物理上的最高点是B点。设小球能通过B点的临界速度为vB,由牛顿第二定律和向心力公式得,解得。
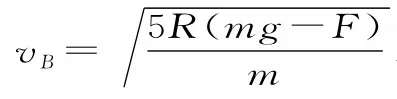
例3一内壁光滑的环形细圆管位于竖直平面内,环的半径为R(比细管的内径大得多),圆管中有两个直径比细管内径略小的小球A、B(可视为质点)。小球A的质量为m1,小球B的质量为m2,它们沿环形细圆管顺时针运动,经过最低点时的速度都为v0。设小球A运动到最低点时,小球B恰好运动到最高点,若要此时两小球作用于圆管的合力为零,请写出用m1、m2、R来表示v0的关系式。
解析
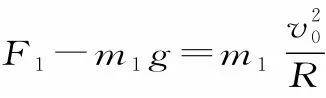
点评:本题涉及的物理模型是轻杆模型,但是题目的设问“不按常理出牌”,要求考生根据题目所给条件写出m1、m2、R来表示v0的关系式,有的同学看到题目就会有无从下手的感觉,导致直接放弃求解。
感悟与提高
1.如图4所示,一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥形筒固定不动,有两个质量相等的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则以下说法中正确的是( )。
A.小球A的角速度等于小球B的角速度
B.小球A的线速度大于小球B的线速度
C.小球A的运动周期小于小球B的运动周期
D.小球A对筒壁的压力大于小球B对筒壁的压力
2.如图5所示,半径为R的光滑球体固定在水平面上,从球体的最高点A由静止释放一个质量为M的小滑块,求小滑块在下滑过程中离开球体时的位置和速率。
3.如图6所示,轻杆OA的长度l=0.5 m,A端固定一质量m=3kg的小球,小球以O点为圆心在竖直平面内做圆周运动,取重力加速度g=10 m/s2。当小球通过最高点的速率为2m/s时,求轻杆OA受到的力。
参考答案:1.B
3.轻杆OA受到大小为6N的压力。

