催化裂化管式待生剂分配器颗粒分配特性及内部流动特性的CPFD模拟

杨赛飞， 张永民， 付明义， 杨智君

(1.中国石油大学 重质油国家重点实验室，北京 102249；2.山东京博石油化工有限公司，山东 滨州 256500)

再生器作为炼油厂流化催化裂化(Fluid catalytic cracking，简称FCC)装置的重要组成部分，其主要作用是利用空气烧掉裂化反应后附着在催化剂上的焦炭，从而恢复其活性[1]。工业中要求再生后催化剂的炭含量尽可能低，且消耗尽可能少的空气，以降低装置能耗。然而，在传统设计的再生器中，很多装置没有设计分配待生剂的结构，待生剂通过待生循环斜管直接输送进入再生器，导致待生剂在再生器横截面上分布极不均匀，因而难以实现待生剂上焦炭与主风中氧气的均匀接触，不仅造成再生烧焦强度的降低以及装置整体能耗的增大，更甚者还可能造成稀相尾燃，从而危及装置安全平稳操作。目前，随着国内FCC装置的大型化发展，再生器的直径不断扩大，待生剂在再生器内分布不均的问题日益突出。

近年来，为了提高再生器的再生效率，国内外研究者逐渐认识到待生剂分配器的重要作用，开始提出和应用不同的新型待生剂分配器结构。Chen和Patel[2]提出了一种顶部带有水平分配口的待生剂提升管，待生剂从该提升管底部引入，在提升风的作用下，从顶部水平分配口流入再生器床层顶部，提升管顶部出口结构有利于待生剂从多个水平分配口均匀流出。然而，这种结构需要消耗的提升风量较高，部分提升空气还有可能直接走短路离开密相床层，容易加剧再生器尾燃的风险，且容许设置的水平分配口有限，待生剂的分配均匀性还有待提高。Myers等[3]提出了一种类似树枝状气体分布器的待生剂分配器结构，待生剂首先进入一个小型流化床，之后再流入带有主管和支管结构、略向下倾斜的树枝状待生剂分配管，分配管上设置有很多催化剂流出孔，分配管内部设置有流化催化剂颗粒的气体分布管，其设计思想是利用气体分布管流入流化风的帮助，使催化剂实现较好的流化状态，从而能像液体一样从众多颗粒流出孔中均匀地流入再生器床层顶部。但是，这种气体分布管设计很难实现所有待生剂分配管内颗粒的流化，一旦部分催化剂没有很好地流化，则会形成阻碍其他催化剂颗粒继续流动的障碍，因此很难实现待生剂颗粒整体分配的均匀性。

Benjamin等[4]提出了一种和Chen和Patel[2]类似原理的待生剂分配器，待生剂颗粒首先被引入一根水平输送管，输送管一端通入输送风使得颗粒以稀相气力输送的方式流到垂直向下的下行输送管，下行管底部设置有多个喷嘴，输送风和待生剂颗粒一起从喷嘴出口喷射进入再生器床层。张振千等[5]提出了一种水平主管和倾斜向下支管的管式待生剂分配器，水平主管中设置有改善催化剂流动性的流化风分配管，在流化风的作用下，待生剂流入倾斜向下的支管中，在重力作用下通过设置在支管上颗粒分配口流入再生器。该结构和Myers等[3]提出的结构类似，在主管中存在局部颗粒失流化阻碍其他颗粒流动的问题，支管中由于没有流化风，在重力作用下很难实现颗粒沿所有分配口均匀分配。

张永民等[6]根据空气输送斜槽原理开发了一种新型槽式待生剂分配器。该分配器是由上部物料输送槽和下部通风槽构成，颗粒分配口设置在上部槽体两侧，槽体之间用多孔分布板隔开。在流化风作用下，待生剂进入分配器后在上部输送槽内实现良好的流化状态，从而可以实现从多个侧方分配口均匀流入再生器内。张永民等[7]利用一套可实现催化剂连续循环操作的大型冷模实验装置检验了依据现有工业设计的管式分配器和船型分配器时的颗粒分配性能，得出管式分配器的性能优于船型分配器。新型槽式待生剂分配器的冷模实验研究[8]表明，该结构可以在较小流化风量下实现待生剂的均匀分配，分配均匀性显著优于传统的船型和管式分配器，且具有较大的操作弹性和较小的流动阻力，不会影响待生输送管路的颗粒输送能力。但是，该冷模实验的缺点是只能测量各出口催化剂颗粒的流量和分配比，无法对分配器内气-固流动特性进行详细观察和准确测量，也无法准确测量各出口气体流量的大小和分布。

近年来，随着计算机技术及颗粒流体动力学的快速发展，Snider[9]提出了一种基于欧拉-拉格朗日方法的计算颗粒流体动力学(Computational particle fluid dynamics，简称CPFD)新方法。CPFD基于多相质点网格法(Multiphase particle-in-cell method，简称MP-PIC)[10-11]，对具有相同密度、体积、速度及位置的颗粒进行打包处理，同时采用正应力梯度来简化计算颗粒间的相互作用，从而使得颗粒数目达数十亿的工业级流化床欧拉-拉格朗日模拟成为可能。

笔者在前期实验研究基础上，运用CPFD多相流模型对工业装置中较为普遍应用的一种待生剂分配器型式——管式待生剂分配器进行系统的数值模拟研究。管式待生剂分配器不仅常用于催化裂化装置中待生剂分配，也常用于外取热器中冷催化剂在再生器中的分配。本研究的模拟对象是前期冷模实验中[7]采用的管式待生剂分配器模型，首先模拟输送风和松动风对分配均匀性的影响规律，利用已有实验数据检验所用CPFD模型的可靠性和准确性，然后进一步考察分配器倾斜角度对颗粒分配均匀性的影响。在模拟过程中，同时还考察了分配器内部流动特性以及出口气体流量分布特性的变化规律。

1 数学模型

1.1 控制方程

在CPFD数学模型中，气相被视作连续相，采用欧拉法进行计算，而颗粒相被视作离散相，采用拉格朗日法求解。其控制方程如下：

气相连续方程：

(1)

气相动量方程：

(2)

单位体积相间动量交换速度：

(3)

反映颗粒分布函数f随时间变化的Liouville方程：

(4)

颗粒加速度方程：

(5)

颗粒正应力方程：

(6)

颗粒体积分数方程：

(7)

1.2 曳力模型

在气-固流化床模拟中，气-固相间的相互作用主要由曳力模型来描述，因此选择合适的曳力模型对于模拟结果的准确性具有重要的影响[12-13]。较为常用的曳力模型有Wen-Yu模型、Ergun模型、Turton&Levenspiel模型及Gidaspow模型等。笔者选用了经典的Gidaspow曳力模型[14]来模拟。该模型结合了适用于稀相系统的Wen-Yu曳力模型[15]和适用于密相系统的Ergun曳力模型[11]，其施加在颗粒上的曳力可表示为：

(8)

本研究对应的前期实验[7]中颗粒相最大堆积体积分数为0.63(堆积密度比真实密度)，且考虑到本研究体系有稀相到密相的过渡区域，因此选用修正的Gidaspow曳力模型[16-18]，即Wen-Yu方程和Ergun方程组成的混合模型。

当颗粒体积分数小于0.75θcp时，采用Wen-Yu方程计算曳力：

(9)

(10)

当颗粒体积分数大于0.85θcp时，采用Ergun方程计算曳力：

(11)

为避免稀相到密相的过渡区域中由于曳力系数不连续引起的数值问题，当颗粒体积分数在0.75θcp和0.85θcp之间时，采用过渡方程计算曳力：

(12)

其中Re为雷诺数，用下式计算：

(13)

rp为颗粒半径，表达式如下：

(14)

2 模拟设置

2.1 几何模型与网格划分

本模拟所采用的几何模型是张永民等[7]前期采用的一套评价待生剂分配器性能的大型冷模实验装置中所用的模型。由于本研究重点关注管式分配器内的气-固流动特性及颗粒分配均匀性，这里对模拟对象进行了简化，即只模拟管式分配器部分，如图1所示，省去了其上方的流化床、下部的颗粒集料仓和提升管等部分。实验中的管式分配器是一根内径为90 mm，厚为5 mm的有机玻璃管，其入口端与待生剂斜管的水平管段相连，末端使用盖板封闭。在水平管段左侧同心安装了1个直径为26 mm的输送风管。同时，在分配器两侧分别交错地开设了10个直径为26 mm、等间距布置的排料口。此外，为了松动和流化分配器底部的颗粒，在其下方排布了19个直径为6 mm的短管来通松动风。

图1 前期实验中采用的管式待生剂分配器[7]
Fig.1 Pipe spent catalyst distributor used in the previous experiments[7]

在模拟中，管式分配器的几何模型如图2所示，其几何结构与实验装置基本一致。为了便于直观地观察各个出料口颗粒的流出情况，在管式分配器的外围设置了1个方形计算域(2100 mm×160 mm×170 mm)。管式分配器的长度和直径分别为 1900 mm 和90 mm。由于在网格划分时分配器两侧的10个圆形排料口难以捕捉，因此将其简化为10个方形出口(26 mm×26 mm)。Barracuda软件采用笛卡尔网格切割单元法对几何模型进行网格划分。经网格无关性验证之后，管式分配器的网格划分如图3所示，网格总数为44982。

图2 模拟中管式待生剂分配器几何模型的主视图和左视图Fig.2 Main view and left view of the geometric model of the pipe spent catalyst distributor in the simulation(a) Main view; (b) Left view

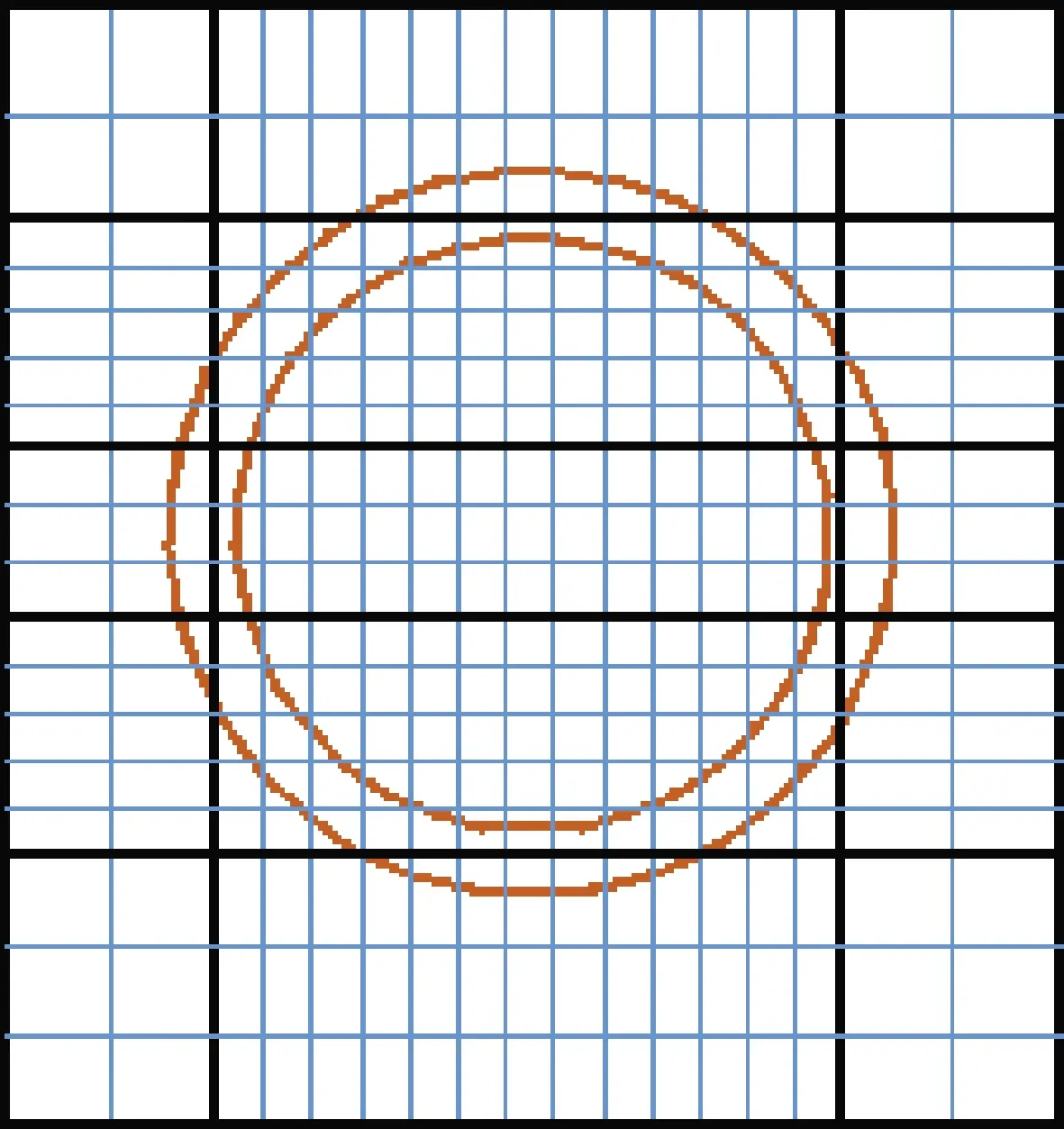
图3 管式待生剂分配器的网格划分Fig.3 Meshing of the pipe spent catalyst distributor

2.2 边界条件及模拟参数设置

在图2中，管式分配器的左端为颗粒入口边界和输送风入口边界。颗粒选用FCC平衡催化剂，密度为1500 kg/m3，最大堆积体积分数为0.63，索特平均直径(Sauter mean diameter)为60 μm，质量流率为1.2 kg/s。输送风选用的气体压力和温度分别为101325 Pa和300 K，密度为1.173 kg/m3，风速为1～6 m/s。在分配器的底部均匀设置了19个射流点源来模拟松动风入口，其位置排布与实验完全一致。采用点源注射的进气方式可以规避因捕捉几何小孔所导致的局部网格过密的问题，进而优化了网格质量和提高了计算速率。松动风选用的也是常温常压空气，风速范围为0～0.55 m/s。分配器外围方形计算域的底部设置为压力边界，只有气体可以排出。为了研究分配器倾斜角对颗粒分配均匀性的影响，模拟中采用分解重力加速度的方法来实现5个不同的分配器倾斜角度(进料端固定，末端向下旋转)，分别为0°、2°、6°、10°和14°。初始状态下，整个计算域只有空气，没有颗粒，压力和温度分别为101325 Pa和300 K。在分配器前后两侧的10个排料口分别设置流量监测面，以此来实时监测由各个排料口流出的颗粒和气体的流量。模拟的时间是20 s，初始模拟时间步长的设置要根据模拟对象先给定，本研究中初始时间步长均设置为0.002 s，其后Barracuda会根据每步计算所生成的CFL值自动调整计算时间步长至合适的大小。

3 模拟结果与讨论

3.1 输送风和松动风对颗粒分配均匀性的影响

为了定量评价待生剂分配器的颗粒分配性能，张永民等[7]在前期实验中提出了一个颗粒分配不均匀指数ξ，其表达式如下所示：

(15)

(16)

其中，ci为各个出料口颗粒实际流出量wi与理想流出量W/n之比。ξ反映了分配器实际分配与理想分配之间的差异性。ξ越大，表明分配器内颗粒分配均匀性越差；ξ越接近于零，表明颗粒横向分配的均匀性越好。

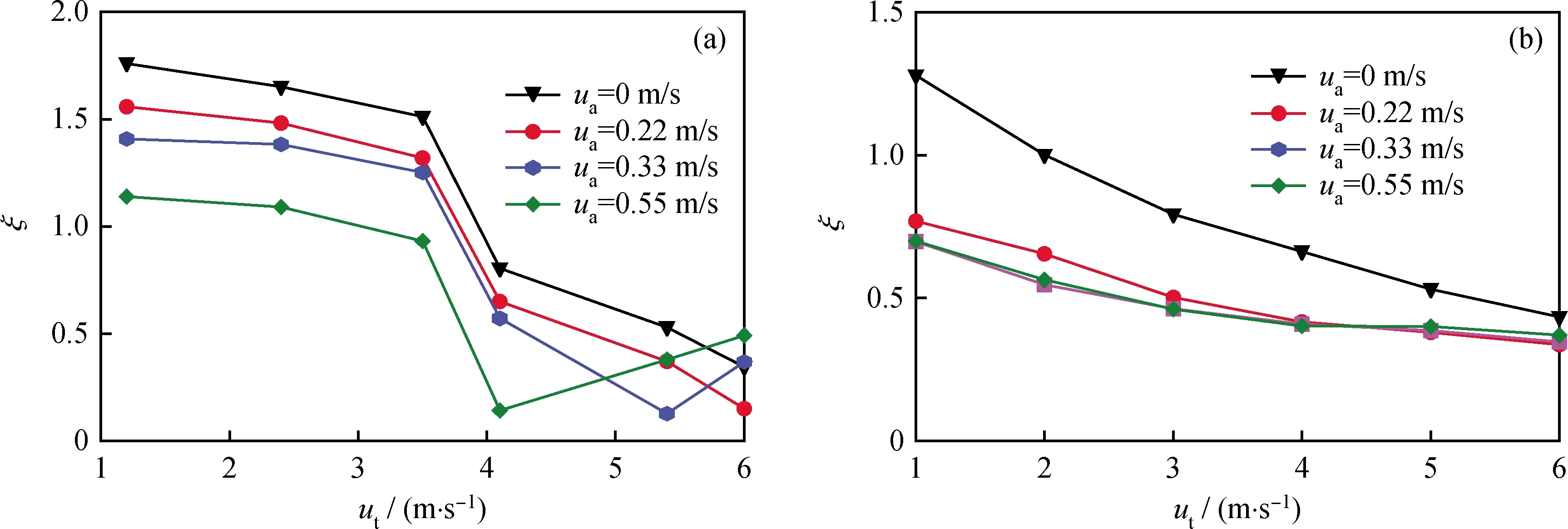
图4 颗粒分配不均匀指数(ξ)随输送风速(ut)和松动风速(ua)的变化Fig.4 Variation of the heterogeneity index (ξ) of particle distribution under different flowrates of transport air (ut) and fluidizing gas (ua)(a) Experimental result; (b) Simulated result

根据稳定状态下(模拟开始15 s后)分配器的10个出料口监测的瞬时颗粒质量流量，可以计算得到各个出料口的平均颗粒质量流量，进而运用式(15)和式(16)得到不同操作条件下的颗粒分配不均匀指数ξ。图4(a)和4(b)分别给出了实验和模拟的ξ随输送风速和松动风速的变化情况。由图4(b)可以看出，随着输送风速的增大，颗粒分配不均匀指数明显减小，增加松动风速能有效改善颗粒横向分配的均匀性，但是进一步增大松动风速后，颗粒分配不均匀指数并无显著变化。出现这种现象的原因是：随着输送风速的增大，颗粒获得了更大的横向动能，进而更容易流向分配器的末端。此外，当在分配器底部注入松动风后，颗粒被流化起来，此时在输送风的作用下，颗粒更容易从分配器末端的出口流出，从而进一步改善了颗粒分配的均匀性。这与前期实验中得到的结论基本一致，即增加输送风和松动风均能改善颗粒的横向分配均匀性，但总体上，松动风的影响不如输送风显著。通过对比图4(a)和图4(b)可以发现，实验结果中不均匀指数ξ在输送风ut>3 m/s时发生陡降，而模拟结果并没有出现。这主要是因为，模拟中省去了分配器前端的水平管段以及与之相连的下料立管，而水平管段与下料立管内的气-固流动形态会对分配器内的气-固流动产生直接的影响，进而影响颗粒分配的均匀性。这在前期实验[7]中有详细的解释，所以从趋势上看，此模拟结果是可靠的。

3.2 倾斜角度对颗粒分配均匀性的影响

在前面的分析中提到，颗粒沿分配器的横向动能是影响颗粒分配均匀性的重要因素，横向动能越大，颗粒越容易向分配器的末端流去。鉴于此，考察了分配器倾斜角度θ对颗粒分配均匀性的影响。图5为输送风速1 m/s时，有无松动风对不均匀指数随分配器倾斜角度变化的影响。与图5相对应，图6为输送风速1 m/s，无松动风时不同倾斜角度下的分配器平均颗粒体积分数云图。

由图5可以看出，当无松动风时，随着倾斜角度的增大，颗粒分配不均匀指数呈现了一个先急后缓的降低趋势，表明颗粒的分配均匀性越来越好。这可以结合图6加以解释，随着倾斜角度的逐渐增大，颗粒在轴向上的重力分量也不断增大，从而获得更大的横向动能，使得更多囤积在分配器前端的颗粒向末端流去。然而，分配器的倾角也不是越大越好，当倾角过大时，大部分颗粒会从靠近末端的出口排出，不利于颗粒的均匀分配。这也是不均匀指数降低程度逐渐放缓的原因所在。当有松动风时，随着倾斜角度的增大，不均匀指数呈先下降后上升的变化趋势，并且在θ=6° 时达到最小，表明颗粒的分配均匀性在该角度时达到最好。造成这种结果的原因与上述无松动风时类似，倾角的增大使得颗粒获得更大的轴向推动力，进而使得颗粒更容易流向分配器的末端；然而，过大的倾角会导致大部分颗粒涌向分配器的末端，导致颗粒分配均匀性变差。总体来看，分配器倾斜角度对颗粒的分配均匀性具有显著的影响，当分配器的倾斜角度在一定范围内时，有松动风的颗粒分配均匀性明显好于无松动风。

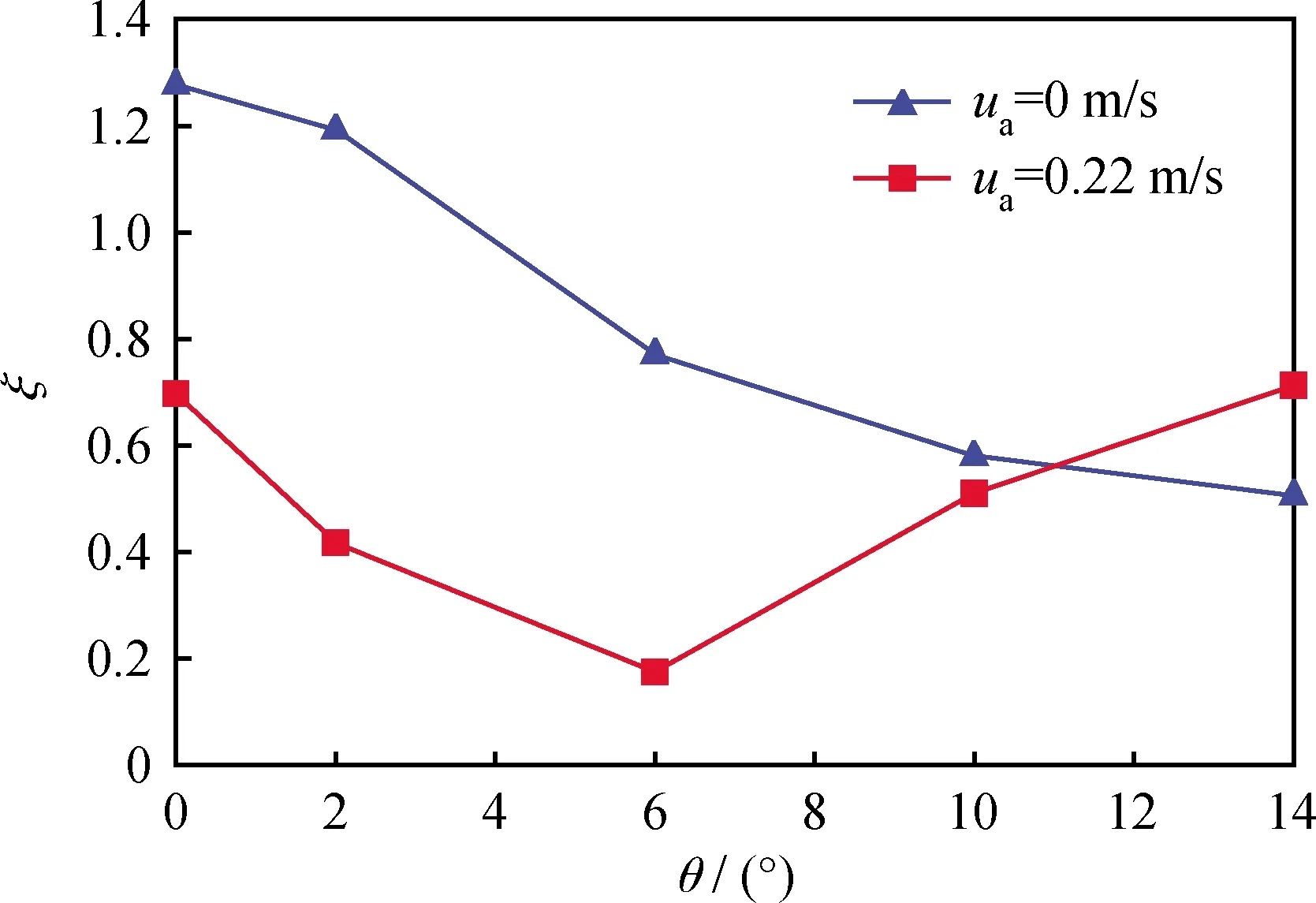
图5 有无松动风时不均匀指数(ξ)随分配器倾斜角度(θ)的变化Fig.5 Change of the heterogeneity index (ξ) under different distributor tilt angles (θ)ut=1 m/s

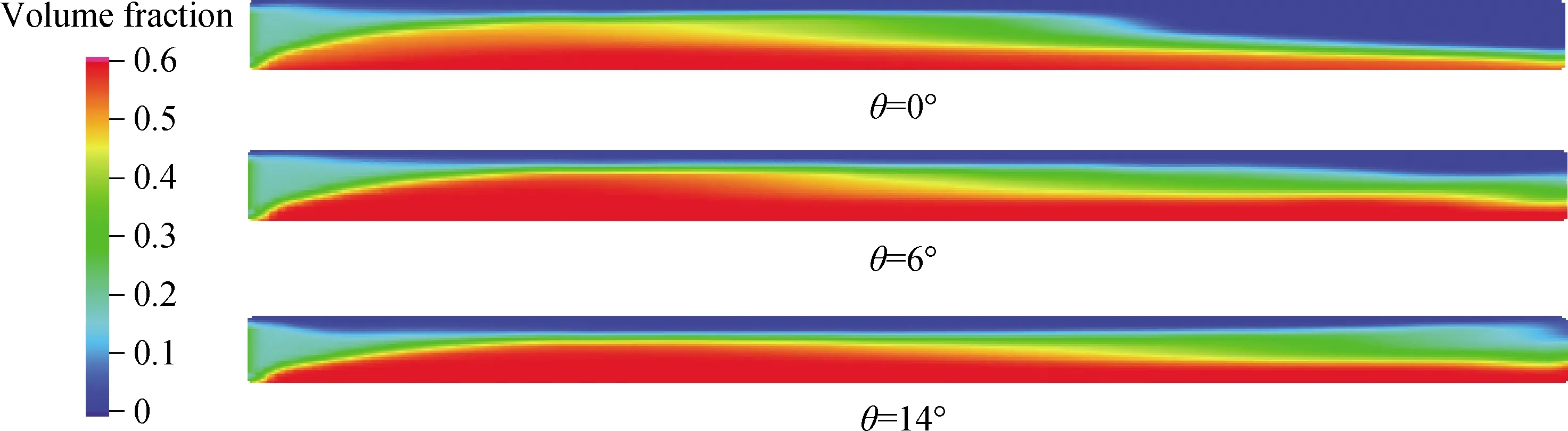
图6 不同倾斜角度下无松动风的分配器内平均颗粒体积分数云图Fig.6 Contours of solids fraction in the distributor at different tilt anglesut=1 m/s; ua=0 m/s

3.3 输送风速和松动风速对各出口颗粒流量的影响

图7为分配器各出口平均颗粒流量随输送风速和松动风速的变化。为了便于区分，将分配器自入口端至末端的10个出料口依次编号为1，2，……10。由图7可以看出，在任意松动风速和输送风速下，均有一个出料口颗粒流量最大，并且随着输送风速的增大，最大出料口的位置会逐渐向分配器的末端移动，同时该出料口的颗粒流量也逐渐减小。此外，与不加松动风(见图7(a))相比，加松动风后分配器各出口的颗粒流量更加接近，颗粒分配更加均匀，并且随着松动风速的继续增大，颗粒分配的均匀性变化不大。出现上述现象主要是因为，输送风速的增大使得分配器入口端更多的颗粒被气体夹带并朝着分配器的末端移动，从而使得分配器前密后稀的颗粒分布状况得到改善。与此同时，当输送风速固定时，增加松动风速可以使得分配器内部尤其是底部区域的颗粒流化起来，增大了颗粒之间的空隙，降低了气体流动阻力，使得更多的颗粒更容易被输送风夹带移动，从而在减少流化死区的同时也使得分配器内的颗粒流动更加顺畅，最终导致各出料口的颗粒流量更加接近。然而，由于松动风主要是对颗粒的纵向运动产生影响，因此进一步增大松动风速对颗粒在分配器内的横向运动影响甚微。

3.4 输送风和松动风对各出口风量的影响

分配器内气体的运动带动了颗粒的流动及排出，反过来，颗粒的分布形态也影响着气体的运动轨迹，进而影响各出口的排风量。图8为有无松动风时各出口排风量占总排风量的百分数随输送风速的变化。由图8可以看出，无论有无松动风，分配器各出口的排风量占总排风量的百分数基本呈现一个中间低两边高的“碗状”结构，并且随着输送风速的增大，分配器中间区域的出口排风量占总排风量的百分数逐渐增大，而靠近分配器末端的出口排风量占总排风量的百分数逐渐减小。当输送风速固定时，与无松动风(见图8(a))相比，加松动风(见图8(b))后，靠近分配器前端的出口排风量占总排风量的百分数略有降低，而靠近末端的出口排风量占总排风量的百分数明显增大。

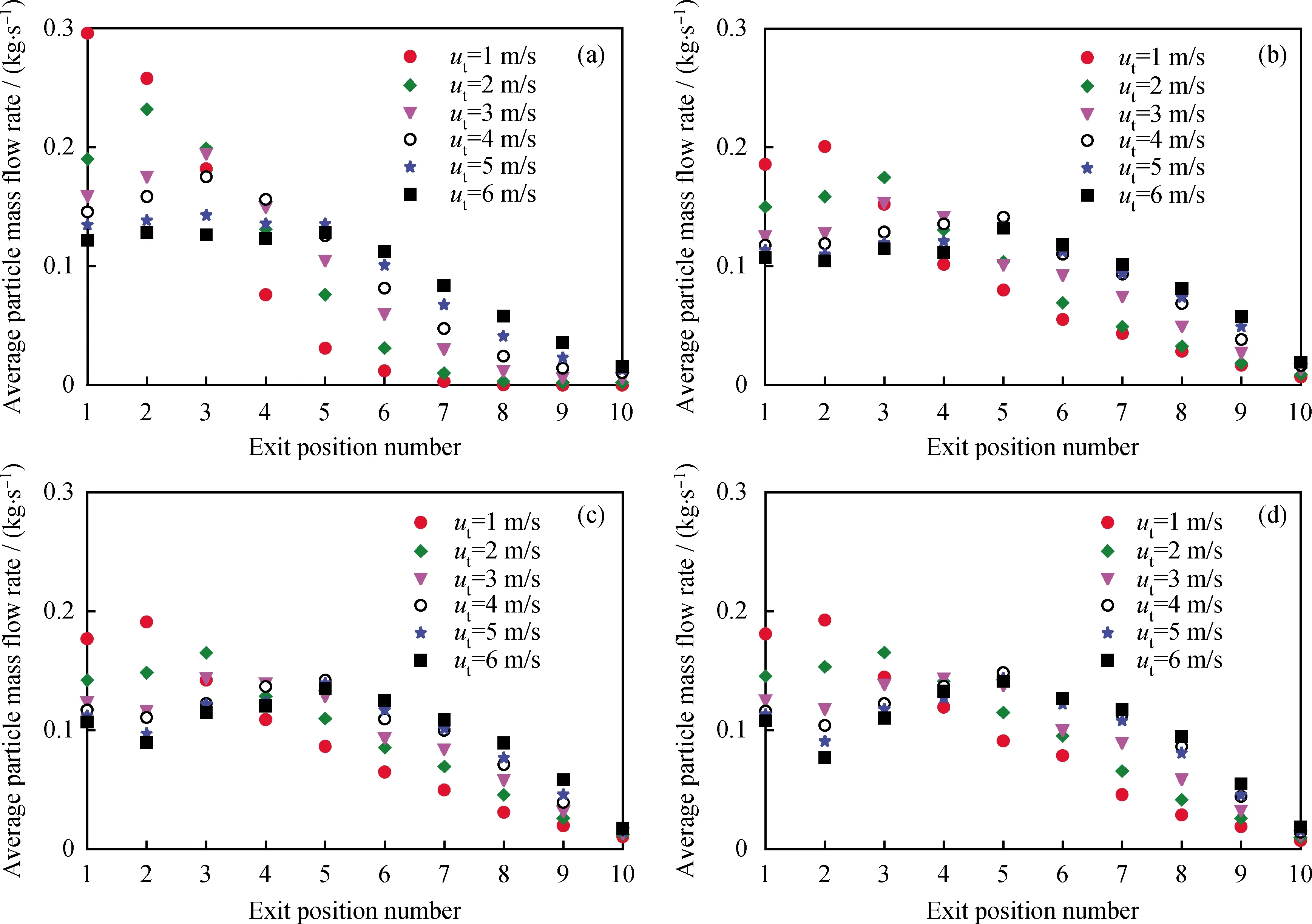
图7 输送风速(ut)和松动风速(ua)对出口颗粒流量分布的影响Fig.7 Effects of the transport air (ut) and the fluidizing gas (ua) on the particle flux distribution at the 10 outletsua/(m·s-1): (a) 0; (b) 0.11; (c) 0.22; (d) 0.55

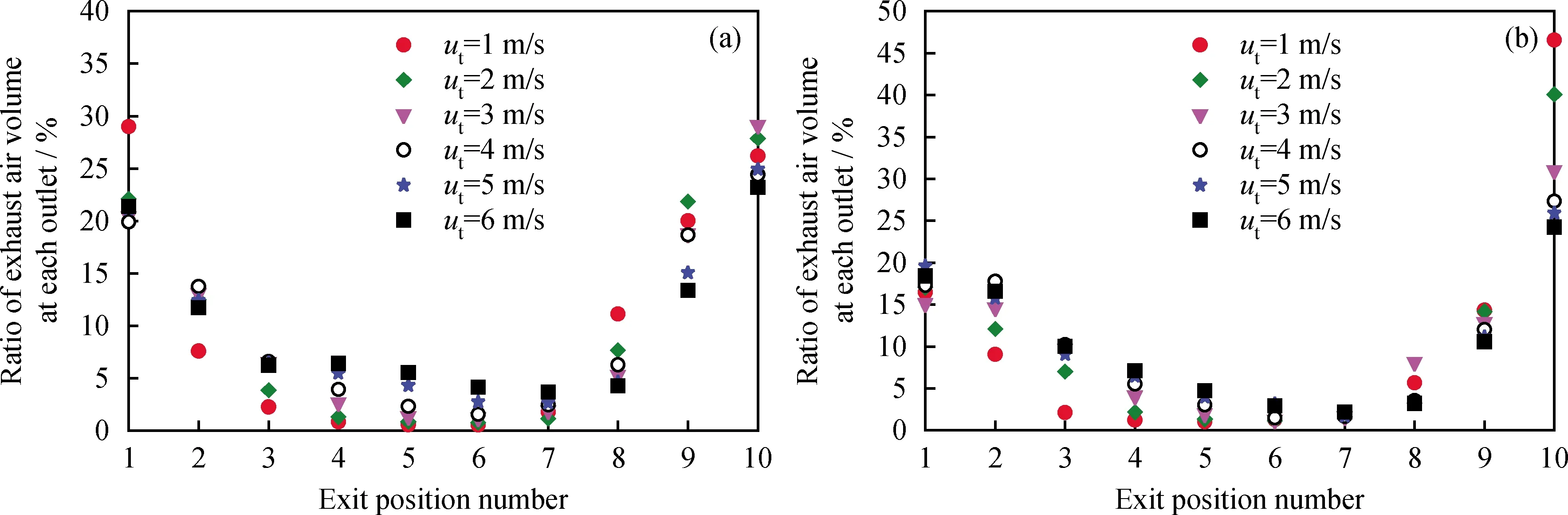
图8 输送风和松动风对出口气体流量分布的影响Fig.8 Effects of transport air and fluidizing gas on the air flow distribution at the 10 outletsua/(m·s-1): (a) 0; (b) 0.22

上述现象可以结合管式分配器有无松动风时的平均颗粒体积分数云图得到很好的解释，如图9所示。由图9可见，无论有无松动风，颗粒均主要集中在分配器的中间区域，导致气体优先从分配器的前端和末端的出口排出，进而形成了图8中所示的“碗状”分布。随着输送风速的增大，当无松动风时，更多中间区域的颗粒被夹带到分配器的末端，使得更多的气体可以从中间的出口排出；当有松动风时，由于分配器内的颗粒被流化起来，颗粒间空隙率增大，更多的气体可以穿过颗粒间隙从中间的出口排出，因而两者均导致了分配器排风量占总排风量的百分数在中间出口增大而在末端出口减小的趋势。通过对比图9(a)和图9(b)可以看出，加松动风后，分配器内的颗粒在纵向上的高度明显降低，使得输送风更容易从颗粒上方的无阻力区流向分配器末端的出口，从而导致靠近末端的出口排风量占总排风量的百分数显著提高。

图9 管式分配器有无松动风时的平均颗粒体积分数云图Fig.9 Comparison of solids fraction contours in the pipe distributor with and without fluidizing gas(a) ua=0 m/s; (b) ua=0.22 m/s; ut=1 m/s

4 结 论

(1) 采用CPFD方法模拟得到的颗粒分配不均匀指数随输送风速和松动风速的变化趋势和数值上总体与实验结果相吻合，从而验证了CPFD模型模拟待生剂分配器气-固流动特性的可行性。同时进一步说明了增加输送风和松动风能改善颗粒分配的均匀性，但松动风的改善效果不如输送风显著。

(2) 待生剂分配器倾斜角度对颗粒分配的均匀性具有显著的影响，增大倾角能有效降低分配不均匀指数，但倾角过大时，颗粒的分配效果反而变差。在本研究中，当倾角θ=6°时，颗粒的分配均匀性达到最佳。鉴于此，可以考虑改变目前工业装置中常采用的水平管式分布器结构，使其倾斜一定的角度以达到更好的颗粒分布均匀性。

(3) 随着输送风速的增大，出料流率占比最大的出口逐渐远离分配器入口端，并且该占比也逐渐变小。与不加松动风相比，加松动风后分配器各出口的颗粒流量更加接近，颗粒的分配均匀性更好。

(4) 分配器各出口的气体流量分布呈“碗状”结构，即两端高中间低的趋势，这与分布器内颗粒料层的高度分布有关。输送风速的增大有助于缩小各出口气体流量的差距。

符号说明：

英文符号：

ci——某个出料口颗粒实际流出量与理想流出量之比；

Cd——曳力系数；

C1——线性系数；

C2——非线性系数；

dp——颗粒半径，m；

D——气-固相间曳力系数；

D1——颗粒体积分数小于0.75θcp时，采用Wen-Yu方程计算曳力，N；

D2——颗粒体积分数大于0.85θcp时，采用Ergun方程计算曳力，N；

Dp——颗粒相间曳力系数；

f——颗粒概率分布函数；

i——出料口编号；

mp——颗粒质量，kg；

n——出料口个数；

P——气相压力，Pa；

PS——常数，Pa；

rp——颗粒半径，m；

Re——雷诺数；

t——时间，s；

ua——松动风大小，m/s；

ut——输送风大小，m/s；

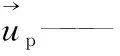
Vp——颗粒体积，m3；

W——颗粒流出总量，kg；

wi——某个出料口颗粒实际流出量，kg；

希腊符号：

β——常数，被设置为默认值3；

ε——一个数量级为10-7的常数；

τg——非静力应力，N/m2；

τp——颗粒正应力，N/m2；

θ——分配器倾斜角度，°；

θcp——颗粒最大体积分数；

θg——气体体积分数；

θp——颗粒体积分数；

ρg——气体密度，kg/m3；

ρp——颗粒密度，kg/m3；

μg——气体动力黏度，Pa/s；

ξ——颗粒分配不均匀指数；

下标：

p——颗粒相；

g——气体相。