基于信息甄别的公益性农业技术推广机制研究
江喜林 夏 晶 刘丽娜
(湖北师范大学经济管理与法学院,湖北 黄石 435002)
0 引 言
在传统农业向现代农业转型的过程中,农业技术推广是一个重要环节。农业技术按经济属性可分为经营性农业技术和公益性农业技术。经营性农业技术的推广通过对市场机制的充分利用呈现良好形势,而公益性或半公益性的农业技术推广则存在不少突出问题。公益性农业技术由于其公共物品属性,推广一直是一个难点问题。
学界对于公益性农业技术的推广进行了一些重要研究。一些学者强调市场机制的作用,吴春梅[1]、李艳军[2]等持有此观点。另一些学者强调了公共机构干预的重要性。Miranda和Gary指出商业性推广机构的覆盖面有限,从而公共财政资助是必须的[3]。智华勇等的实证研究表明,政府投入不足是公益性农技推广供给不足的重要原因[4]。旷浩源、应若平指出,缺少公共部门的充分参与与干预是半公益性的农业技术推广处于困境的主要原因[5]。有一部分学者关注农业推广公益性职能与经营性服务的分离。何小凡等认为,新一轮农业推广改革的核心是公益性职能和经营性职能的划分[6]。黄武从激励机制和农业技术的属性等方面分析了公益性和经营性的农技推广分离难的原因[7]。郑家喜、宋彪揭示了基层公益性农技推广在公益性服务和商业性服务之间协调的困难。还有部分学者研究了农户分化背景下农业技术的推广问题。修孟源的实证研究指出,农户兼业化程度与农业技术需求呈反方向变化[8]。赵连阁的研究表明,农户的兼业行为对农户的农业技术采纳行为具有影响[9]。焦源等构建了一种基于农户分化的需求导向型农业技术推广新机制[10]。从农技推广的构成要素来看,农技推广是国家、基层农技推广主体与农民三者之间不断博弈与寻找各自最优选择的过程。公益性农业技术推广是有成本的活动,而且在农户分化的条件下,面临着信息不对称和逆向选择问题。政府如何在信息不对称的条件下,进行社会福利和推广成本之间的权衡是需要研究的重要问题。本文基于农户的异质性构建一个信息甄别模型分析农技推广公共部门和农户之间的博弈,以揭示公益性农技推广过程中公共部门如何在异质性农户间配置资源才能达到最优。
1 模型假设
考虑一种新的生产要素,可以是一种新型种子、农药、除草剂或化肥。农民使用新要素的边际成本和边际收益分别为c和θ,新要素由于生产成本或者外部性的原因,导致其对农业生产者的边际收益小于边际成本,即θ 新要素使用的私人价值为R(q)-C(q),即私人使用要素的边际收益和边际成本之差,社会价值为R(q)+E(q)-C(q),即新要素使用产生的私人价值与外部效应之和。当-E(q) 若政府对θi类型的农户给予的补贴为ti,类型i农户的利润函数定义为Li(q)=q(θi-c)+ti,i=1,2。政府从对类型i农户的补贴中获得的效用为Ui=(θi+e-c)qi-X(ti),i=1,2,其中X(ti)表示政府的资金成本。此外,约定c-e≥0。政府的效用函数定义为U=U1+U2。政府需要规定公益性农业技术推广过程中与农户的契约条款,从而满足预期社会福利最大化的要求。根据显示原理,政府可以通过最优显示机制来解决这一问题,这样一个显示机制涉及一组激励相容的契约(q1,t1)、(q2,t2)。政府需要设计这样两个合同(q1,t1)、(q2,t2)以供两个类型的农户选择,其中,类型i的农户会选择合同(qi,ti),而不会选择合同(qj,tj),j≠i。 若政府的资金成本是线性的,即X(t)=λt,其中,λ>0,λ表示公共资金的影子成本,在这里,为计算简便,令λ=1,因此,X(t)=t。考虑政府的参与约束,政府干预新要素使用的条件是(2c-e)/2≤θ2≤c,它的含义是类型2农户使用要素的社会价值和政府对其支持的边际效用都不为负。这样规定的依据是:可以由此导出2θ2+e-2c>0,结合θ2-c≤0可知,θ2+e-c>0,即类型2的农户使用要素的私人价值和社会价值都是非负的,而且政府对其进行支持的边际效用为正,符合政府的参与约束。 政府在规划过程中,以下条件是需要满足的: (θi-c)qi+ti≥0,i=1,2 (1) (2) (θ1+e-c)q1+(θ2+e-c)q2-(t1+t2)≥0 (3) 政府应该选择一对在式(1)至式(3)的约束条件下能使政府效用最大化的契约,也就是使(θ1+e-c)q1+(θ2+e-c)q2-(t1+t2)最大化。其中,第一个约束条件是类型i农户的参与约束,即农户只有获得利润非负时,他才会愿意购买并使用新要素,第二个约束条件是政府的预算约束,第三个约束条件是政府的参与约束,即政府从支持中获得的效用不能为负。 (4) 图1 线性成本下的最优契约 假设政府的资金成本X(t)是非线性的,且X′(t)>0,X″(t)>0,即资金的边际成本为正且递增。在这个条件下,θi+e-c>0,i=1,2。政府需要在式(1)成立及政府效用非负的条件下最大化(θ1+e-c)q1+(θ2+e-c)q2-X(t1)-X(t2)。由于U/ti=-X′(ti)<0,因此,ti越小对于政府越有利。由于是完全信息,即政府完全了解农户的真实类型,为实现效用最大化,同线性成本时的情况,政府会把ti定在ti=(c-θi)qi的水平上,因此,约束条件式(1)是紧的。因此,模型的一阶条件为(θi+e-c)-(c-θi)X′(ti)=0,i=1,2。若令X′-1(·)=Φ(·),则由一阶条件得非线性成本下的最优契约:Φ(Zi)/(c-θi),i=1,2,其中,Zi=(θi+e-这里对预算的处理是:预算能支持最优合同易证,因为,Zi是关于θi的严格递增函数,Φ(Zi)是关于Zi的严格递增函数,且1/(c-θi)是关于θi的严格递增函数,因此也是关于θi的严格递增函数。政府的无差异曲线是递增的凹函数。因为ti=X-1(qi(θi+e-c)-Ui),得所以ti关于qi是严格递增且是凹的。 如图2,最优契约用B点和A点表示,B点和A点代表的契约分别是给类型1和类型2的农户设计的。在B点和A点,两类农户的利润都为零,参与约束满足。对于类型2的农户来说,选择B点优于A点,因为选择B点可以获得正利润,选择A点只能获得零利润。而对于类型1的农户来说,选择政府为其设计的合同即B点最划算,若选择A点则得不偿失。因此,类型2的农户有伪装成类型1的动力,但由于是完全信息,政府能观察到农户的真实类型,所以伪装的动机不能得逞。 图2 不完全信息下非线性成本时的最优契约 不完全信息在这里是指政府在发放补贴之前不了解农户的真实类型,政府面临的问题是,确定一对契约(q1,t1)和(q2,t2)使预期效用最大化,由于此一对契约是激励相容的,因此,需要满足: (IC1)(θ1-c)q1+t1≥(θ1-c)q2+t2 (5) (IC2)(θ2-c)q2+t2≥(θ2-c)q1+t1 (6) 这两个契约还需满足个人理性约束条件: (IR1)(θ1-c)q1+t1≥0 (7) (IR2)(θ2-c)q2+t2≥0 (8) 政府在式(5)至式(8)的条件下选择一对契约使预期效用最大化,也就是使下式最大化: α[q1(θ1+e-c)-X(t1)]+(1-α)[q2(θ2+e-c)-X(t2)] (9) α[q1(θ1+e-c)-t1]+(1-α)[q2(θ2+e-c)-t2] (10) 其中,i,j∈{1,2}且i≠j。和完全信息时相比,政府的效用函数发生了变化,其中,α和1-α分别表示类型1和类型2的农户所占的份额,第一个约束是激励相容约束,第二个约束条件是参与约束,即农户只有获得利润非负时,他才会愿意购买并使用新要素,第三个约束条件是政府的预算约束。因为IR1和IC2是紧的,容易得U=q1[α(2θ1+e-2c)+(1-α)(θ1-θ2)]+q2(1-α)(2θ2+e-2c),因此有U/q2-U/q1=(1-2α)(2θ1+e-2c)+3(1-α)(θ2-θ1)。可见,一般情况下,U/q2>U/q1都成立,只有在两种情形下,可能有U/q2≤U/q1成立,这两种情况是:α≤1/2且θ1≤(2c-e)/2;α>1/2且θ1>(2c-e)/2。若有α=1/2或θ1=(2c-e)/2两者之一成立,即有U/q2=U/q1成立。在此,令U/q2>U/q1成立,因此,政府会把全部预算都用于支持类型2的农户购买新要素。最优契约为: 同完全信息时一样,假设政府的资金成本X(t)是非线性的,在这里,假设X′(t)>0,X″(t)>0。政府面临的决策问题是在式(5)至式(8)成立的条件下选择一对契约(q1,t1)和(q2,t2)最大化: α[q1(θ1+e-c)-X(t1)]+(1-α)[q2(θ2+e-c)-X(t2)] (11) α(θ1+e-c)-α(c-θ1)X′(t1)-(1-α)(θ2-θ1)X′(t2)=0 (12) 当农户的类型是离散的且具有n种(n>2)时,并且具有上文中的5个性质,那么可以对以上机制进行推广得出如下结论:效率最高类型的农户获得有效配置,其他类型的农户的配置都是次有效的;除效率最低类型的农户之外,其他每种类型的农户的合同与紧邻的比他低一个效率级别的农户的合同无差异;效率最低的农户获得零剩余,其他类型的农户都能获得一个正的剩余,这个剩余随着效率级别的降低而提高。 本文基于农户的异质性和信息不对称建立一个信息甄别模型,分析农技推广过程中政府和农户之间的博弈,揭示政府在农业技术推广的资源分配中,如何避免农户的逆向选择行为,以实现资源配置效率的提高。结论表明:由于高效率农户总是可以通过假装成低效率农户而获得正剩余,而低效率农户伪装的话则得到负剩余,因此,最低效率的农户没有信息租,高效率的农户可以获得信息租,而且信息租随着效率级别的上升而提高;只有效率最高类型的农户获得了有效配置,其他类型农户的配置都是次有效的。 在农户分化的背景下,为促进公益性农业技术的推广,需要做好以下几个方面的工作:首先,对推广对象进行分类,避免推广资金的平均化使用,优先支持农业产业化龙头企业和生产大户;其次,重视不同类型农户的技术需求和信息反馈,提高农户实际需求与推广技术的契合度;最后,政府应通过适当的措施引导发展农业专业合作社,通过各种形式把分散的农户组织起来,农民组织化程度的提高一方面有利于农业技术的扩散,另一方面可以降低政府对于农户的信息不对称程度。2 完全信息下公益性农技推广的最优契约
2.1 情形一:线性成本和预算约束
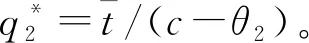
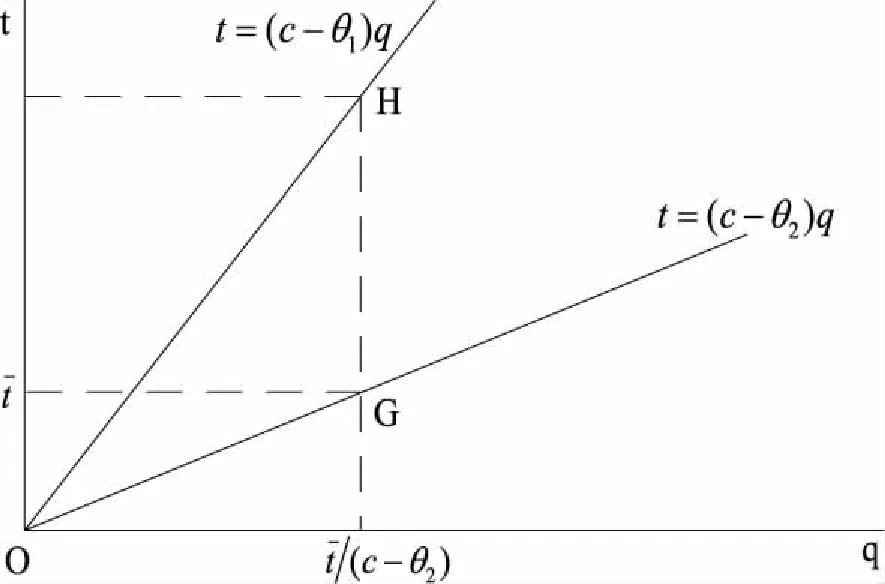
2.2 情形二:非线性成本下的最优契约
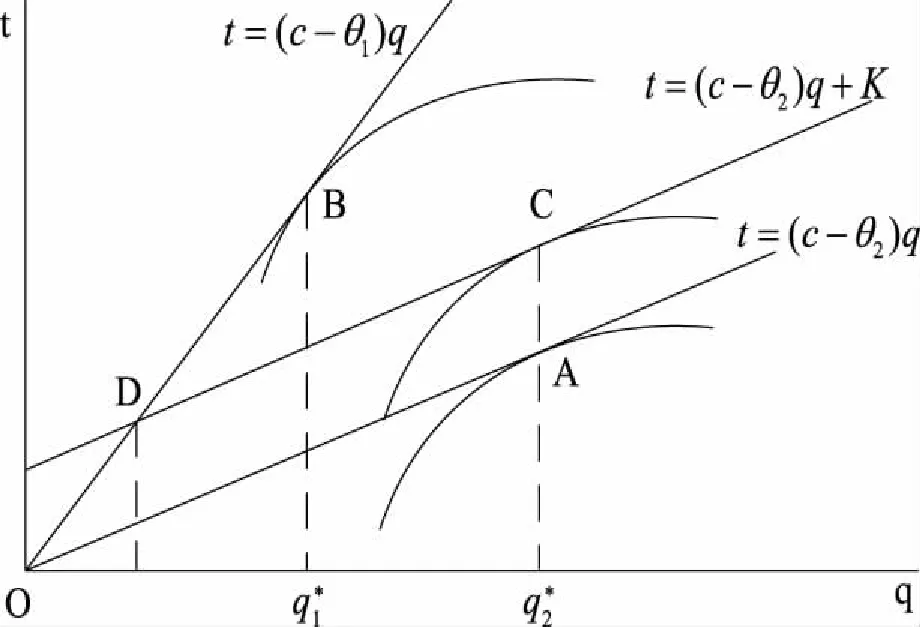
3 不完全信息下政府的信息甄别
3.1 问题的几个性质
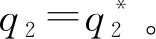
3.2 情形一:线性成本下的最优契约
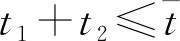
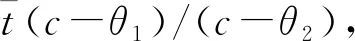
3.3 情形二:非线性成本下的最优契约
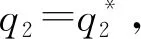
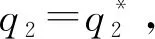
4 结论与建议

