理想状态下的同心鼓策略研究

刘晓扣 管仁永 姜国柱

摘 要：文章研究的是在理想状态下同心鼓的协作最优策略。假设平衡状态后的排球与鼓的碰撞点为定点，考虑空气阻力的影响以及人数的不确定性，研究平衡状态后的运动过程，文章由动量守恒和动能守恒建立微分方程，由目标规划得到了策略模型，最后进行求解，得到最佳策略。

关键词：微分方程;弹性碰撞;目标规划

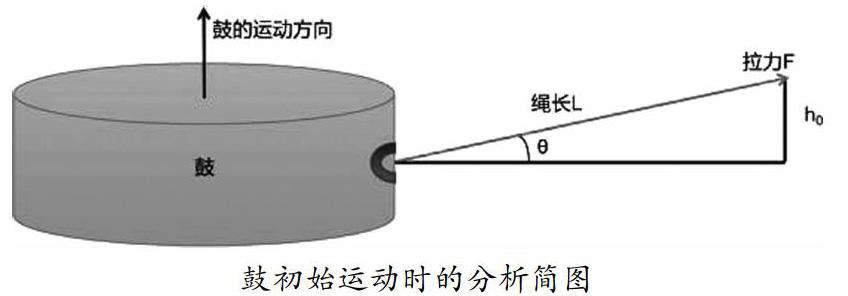
同心鼓扩展项目的目标是使得连续颠球的次数尽可能多。该活动使用的牛皮双面鼓半径r为40cm，高度为22cm，质量m为3.6kg。项目开始时，质量m为3.6kg的球从鼓面中心上方0.4m处竖直下落，队员通过牵拉绳子将球颠起的高度应高于鼓面0.4m，否则项目结束。本文研究了在每个人都可以精确控制用力方向、时机和力度的情况下，团队的最佳协作策略，并计算出该策略下的颠球高度。

1 模型的建立与求解

1.1 基本假设

（1）假设排球与鼓的碰撞为完全弹性碰撞;（2）忽略鼓在运动过程中所受的空气阻力，忽略绳子的质量;（3）假设队员均站立不动，且绕鼓均匀分布;（4）假设排球与鼓的碰撞会趋于一种平衡，平衡后碰撞点为定点;（5）忽略鼓的双面牛皮的质量，且鼓的质量分布均匀。

1.2 问题一模型的建立

Step1.由相关文献[1]可得排球的空气阻力模型：

1.3 模型的求解

（1）由于碰撞不会第一次就达到平衡状态，因此让队员们第一次的发力略大于平衡状态时的用力，使排球與鼓第一次碰撞之后，就达到平衡状态。

（2）从最优策略出发，当上升高度正好为0.4m的时候，每个人的用力达到最小。当每个人的距离正好为0.6m时，绳子的长度达到最短，所用的绳子最少。人工求解目标二元函数的极值点，该极值点为最优解：人数20人，每个人的用力大小为51N，绳长为1.72m，初始位置较绳子水平时的高度为0.2559m。

2 结语

本文对运动过程进行了适当简化，分析了在理想情况下，即每个人都可以精准控制用力时，同心鼓项目的最优协作策略，本文所建立的模型，为同心鼓相关研究提供了依据，对该项活动的开展具有一定的指导意义。

参考文献：

[1]顾伟农，焦峪平.空气阻力对排球正面上手发球水平方向飞行距离的影响实验分析[J].兵团教育学院学报，2002（3）.

作者简介：刘晓扣（1998-），女，汉族，山东济宁人，本科，学生，研究方向为物流管理。