基于城市干道十字路口场景的纯电动汽车两目标优化研究

褚观耀，程 前,，邵毅明，蒋工亮

（1.中国汽车工程研究院，重庆 401122；2.重庆交通大学 交通运输学院，重庆 400074）

随着汽车技术的发展，中国电动汽车市场增长迅猛，成为汽车产业重要的发展方向。电动汽车的销量从2013 年的1 万多辆，到2017 年销量达到77万多辆，增速较快[1]。如何提高纯电动汽车的运行效率越来越受到相关学者的重视。谷靖等[2]对微型纯电动汽车的系统结构和电机参数进行优化设计与匹配选型。宋珂等[3]研究了纯电动汽车传动比对汽车整体性能的影响，对纯电动汽车进行匹配。杨易等[4]基于换挡规律对纯电动汽车动力性进行优化研究。房立存等[5]以电池单体电容为约束变量，对最高车速、最大爬坡度、续驶里程进行单目标函数优化研究。GAO 等[6]研究分析底盘轻量化对汽车性能的影响，并利用仿真软件来优化汽车的动力性和燃油经济性。HALL 等[7]建立纯电动汽车动力性的目标函数，利用电机峰值功率、额定功率进行约束，寻找最优解，提高纯电动汽车的动力性。GONCALVES 等[8]通过增加或减小悬架弹簧刚度来优化汽车舒适性，同时优化整车舒适性来提高整车操作稳定性，寻求操作稳定性的最优解。任洪涛等[9]通过对XH2 纯电动汽车的两挡传动比进行优化，以提高整车的动力性和经济性。张抗抗[10]以最高车速、加速时间和百公里电耗为优化目标，对3 种动力系统匹配方案进行对比选择。

以上研究表明，之前考虑的问题主要是整车性能参数优化研究、优化算法的选择和改进、指标参数优化匹配，且存在以下不足：（1）主要以整车动力性、经济性等单目标、两目标进行优化匹配研究，其中纯电动汽车安全性研究较少。（2）国内外学者一般是对车辆本身单目标、两目标进行优化设计，很少有学者结合道路场景，特别是基于城市干道十字路口的研究更少。

本文首先分析纯电动汽车在城市干道十字路口场景下运行轨迹的安全性和经济性两目标问题，建立纯电动汽车安全性和经济性两目标数学模型，然后利用NSGA-Ⅱ遗传算法求得pareto 最优解，最后提出一种基于NSGA-Ⅱ算法的模糊控制策略，并制定相关的隶属度函数和模糊规则，验证了纯电动汽车多目标优化模型的准确性和可行性，有利于纯电动汽车的开发。

1 城市干道十字路口场景下建立纯电动汽车 两目标优化模型

本文依托最常见的双向四车道来分析南进口直行的纯电动汽车和北进口左转车辆行车时4 种不同行驶轨迹，不同的单车道宽度、左转车辆的速度、纯电动汽车通过十字路口的加速度等几个主要的参数变化，分析研究这些参数变化对纯电动汽车安全性和经济性两目标函数的影响。

由于城市干道十字路口是复杂的场景，在保证建模准确的同时，对其进行简化。在建模前做如下假设：车道数h=4；选取车辆宽度为1.6 m；车道宽度为n，单位m；停车线宽度为l，l=1.5 m；分隔带为r，r=0.5 m；北进口左转车辆速度v1=10 m/s。

1.1 纯电动汽车直行通过十字路口的冲突分析

十字交叉口形态主要分为直行-左转冲突、直行-右转冲突、左转-右转冲突、交叉冲突及追尾冲突等。分析各个冲突形态的冲突特性及形成机理，发现直行车道冲突的4 种相位图造成的危害最大，本文选择直行-左转冲突相位进行研究[11]（图1b），其它3 种冲突同理可得。而造成直行-左转冲突主要是因为车道3 在信号灯由黄灯变成红灯的末端车辆抢行通过，在转弯过程中速度较快，此时车道3 变成红灯，车辆还处于转弯过程；而车道1为绿灯，当车辆直行时有可能和正处于转弯的车辆发生侧碰，如图1 所示。

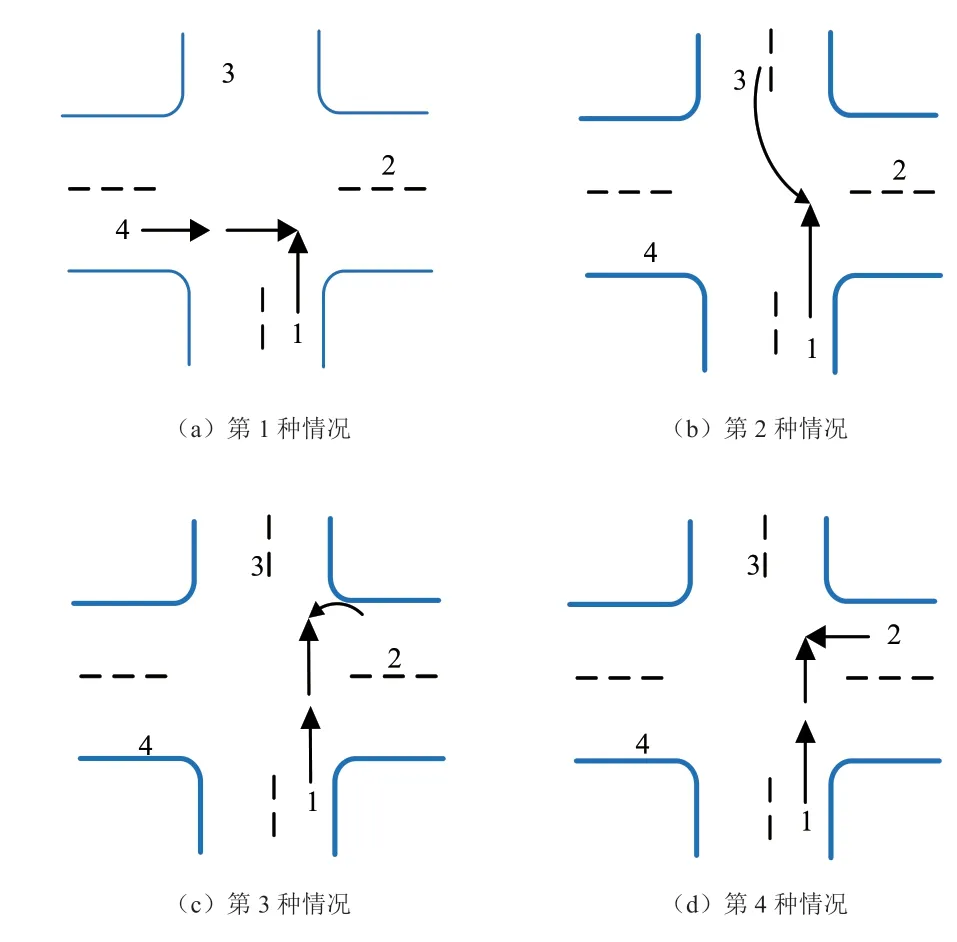
图1 直行冲突示意图

1.2 纯电动汽车直行通过十字路口的安全性分析

1.2.1 建立纯电动汽车安全性目标函数

当北进口左转车辆抢黄灯由停止线通过路口时，与对向南进口直行车辆（由静止状态启动）发生碰撞的概率较大，此时假设若不发生碰撞则左转车辆正常转弯驶入东出口车道，存在4 种不同的行驶轨迹，如图2 所示。

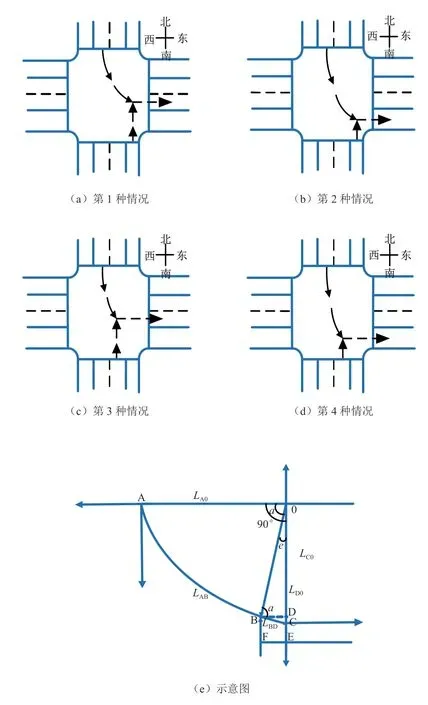
图2 直行-左转车辆行驶轨迹

全文假设左转车辆的行驶轨迹是近似椭圆的一部分，即LAC，如图2e 所示。因此，若左转车辆与纯电动汽车的交点为B，根据车道宽度和车辆宽度推出车辆A 的运行轨迹。

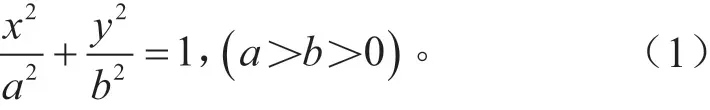
当左转车辆和直行的纯电动汽车存在4 种不同的行驶轨迹时，结合图2 可知，行驶轨迹长半轴a和短半轴b在发生变化，而其它相应数据随之变化。由式（1）可求得：

（a）第一种情况时：

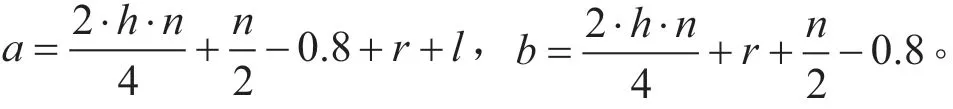
（b）第二种情况时：

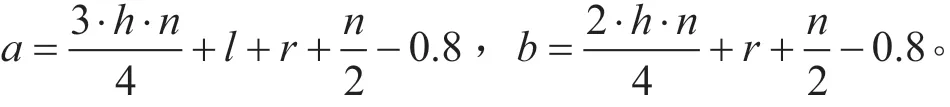
（c）第三种情况时：

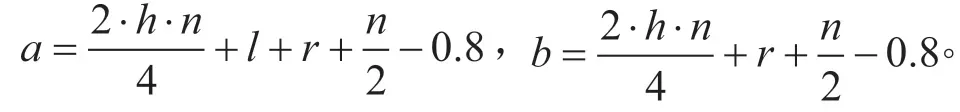
（d）第四种情况时：

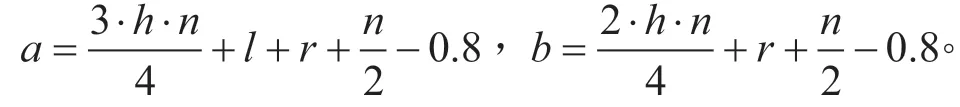
假设左转车辆A 经过LAB的时间为t1，与直行车辆经过LFB的时间为t2。假设a汽 = 车为质+点l，+r当+t2-t1＞0时，不会发生碰撞。由于一般小汽车长度小于5 m，a为 = 安全起+见l，+r取+t2-0t1. 8＞0.5。由图2 可知：

则求得LDO，即

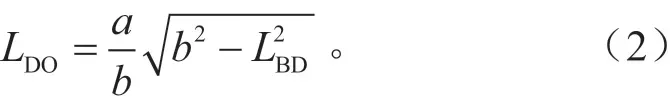
其中，左转车辆A 的行驶轨迹长LAB、直行车辆由停车线到碰撞点的距离LFB分别为：

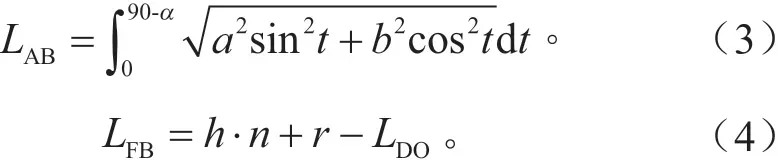
由式（2）、（3）、（4）可求得t1、t2分别为：

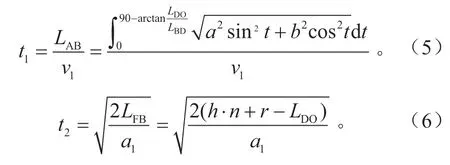
综上所述，当十字路口为双向四车道时，纯电动汽车安全性目标函数Lt为：

1.2.2 纯电动汽车安全性约束条件

北进口左转车辆可以根据行驶轨迹确定其行驶路程LAB，由式（3）和式（4）可确定南进口直行的纯电动汽车到达碰撞点的安全时间t2。因此：

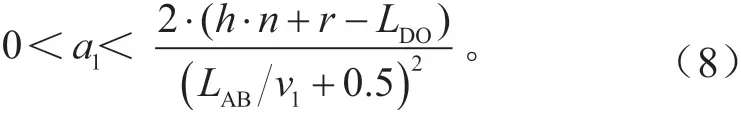
1.3 纯电动汽车直行通过十字路口的经济性分析

1.3.1 整车主要参数

对纯电动汽车而言，整车主要参数对整车性能有着至关重要的作用，对标车型为smart，其基本参数配置参照smart 车型[9]，见表1。

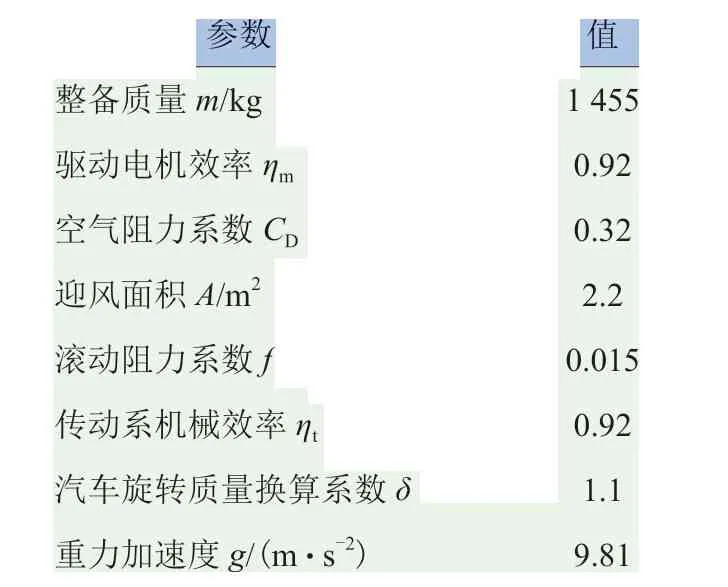
表1 纯电动汽车整车基本参数

1.3.2 纯电动汽车经济性目标函数建立

研究发现我国电动车经济性评价指标主要有续驶里程和能量消耗率。因此，本文选择比能耗数学模型作为经济性的评价方法[10]，当纯电动汽车直线行驶通过十字路口时，在无风条件下主要受到滚动阻力、空气阻力和加速阻力。在每个采样点0.1 s 内认为是匀速行驶的，则在该工况下的能耗为：

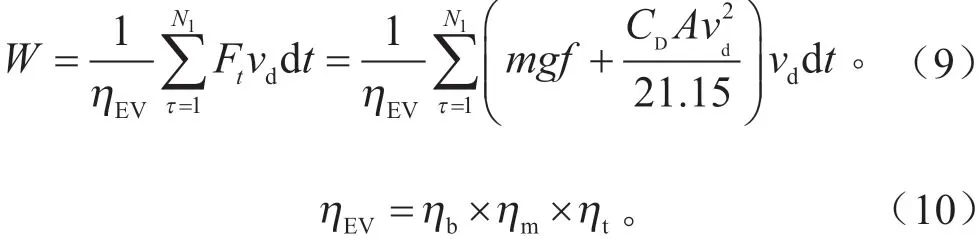
式中：W为加速工况下的能耗，kJ；N1为该工况下的采样点；vd为加速状态下相应采样点的速度，km/h；τ为采样序号；ηEV为整车效率；ηb为电池效率；ηm为驱动电机效率。

比能耗是单位质量、单位里程电动汽车消耗的总能量，即单位里程能耗除以质量。因此，经济性目标函数L6为：

式中：e0为比能耗，(km·h)/(km·t)；iω为比能耗的权重系数；s为行驶里程，km；Le为经济性指标。

1.3.3 纯电动汽车经济性约束条件

根据交通法规可知，当车辆通过十字路口时，最高限速为40 km/h。即约束条件0 ≤vd＜40，单位为km/h。

1.4 纯电动汽车两目标优化目标模型建立

由于在城市主干道十字路口的行驶中，安全性放在首要位置，其次是经济性，权重分别取值为0.7、0.3：

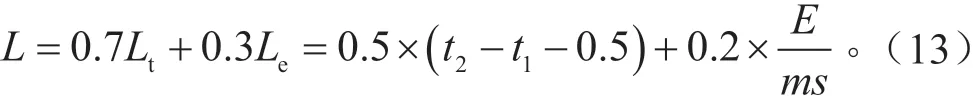
2 纯电动汽车两目标优化研究

为保证纯电动汽车安全性和经济性的非线性优化函数在求解过程中结果全局最优和运算耗时短，通过对比分析选择带精英策略的非支配排序遗传算法（NSGA-II）进行求解。通过对目标函数中的每一项都进行加权，可以灵活考虑其影响，而加权因子的标准是在满足经济性的前提下使安全性和舒适性最大化。其中选择二进制编码，种群个体数目为50个，遗传算法迭代次数为100次，交叉概率为0.97，使用代沟为0.9，变异率为0.001。

2.1 不同行驶轨迹对纯电动汽车加速度的影响

当汽车在双向四车道行驶时存在9 种不同的行驶轨迹，不同的行驶轨迹对应着不同的加速度，影响着车辆的安全性和经济性。假设左转车速v1=36 km/h，车道宽度为n=3.0 m，得到最优纯电动汽车的加速度如图3 所示，计算结果见表2 和表3。

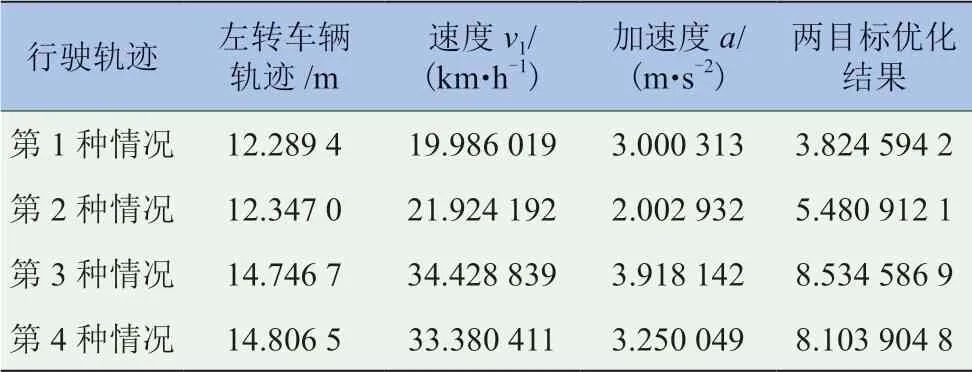
表2 不同行驶轨迹的影响

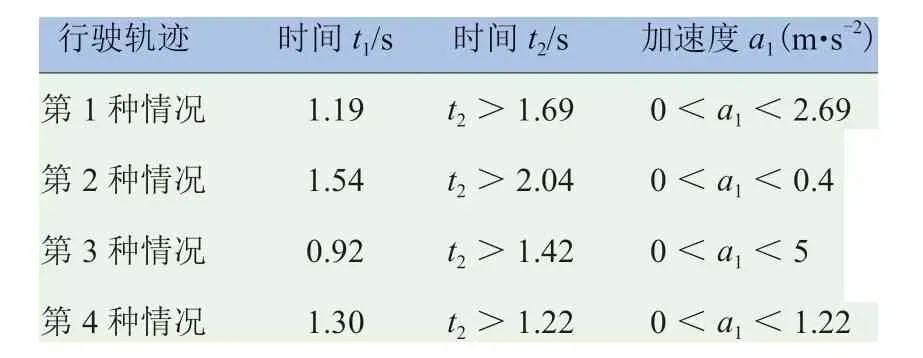
表3 直行的纯电动汽车安全通过十字路口

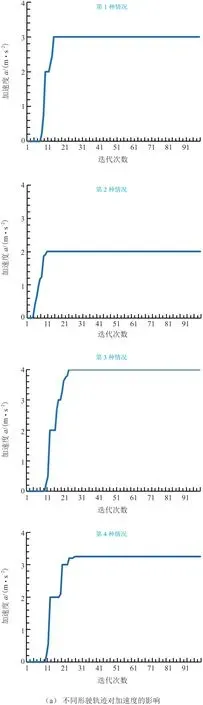
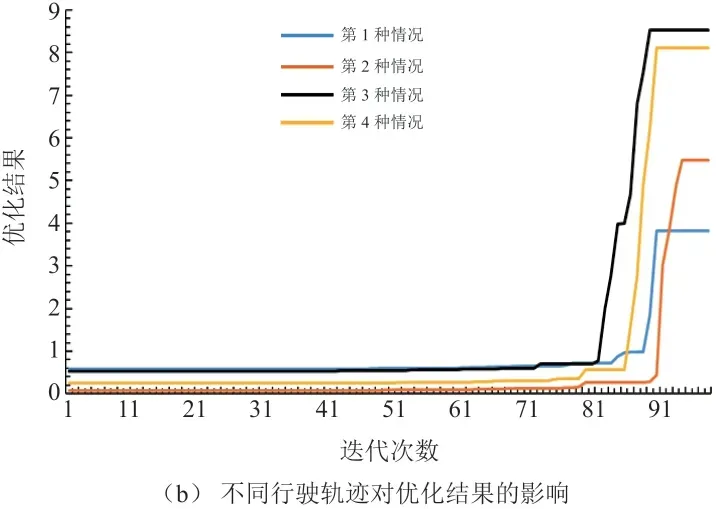
图3 不同行驶轨迹的影响

由图3a 可知，NSGA-II 优化算法刚开始运算时，分布离散，随着迭代次数慢慢增大到13 代时开始收敛形成pareto 最优解，随着迭代次数的增加，加速度目标函数值无明显变化。当北进口左转车辆和南进口直行的纯电动汽车行驶在第3 种轨迹时其加速度达到最大3.918 m/s2。由图3b 可知，NSGA-II优化算法刚开始运算时，优化结果分布离散，当进化至89 代时，纯电动汽车多目标函数值无明显变化，优化结果逐渐收敛形成pareto 最优解。当左转车辆的转弯轨迹由大变小时，直行的纯电动汽车加速度逐渐变大，且逐渐收敛。

结合表2 和表3 可知，当北进口左转车辆和南进口直行的纯电动汽车通过十字路口时，两车行驶轨迹为第3 种情况时两车的安全性能是最好的，且左转车辆行驶轨迹基本上是最大的。南进口直行的纯电动汽车通过碰撞点的时间最短为0.92 s，加速度a1最大为0 ～5 m/s2，在不影响安全性的前提下动力性能也最优，此时北进口左转车辆还未到达而直行的纯电动汽车已经通过了，安全性能最好。

2.2 不同车道宽度对纯电动汽车两目标函数的影响

由于城市主干道单车道宽度标准为3.0～3.5 m，不同的单车道宽度影响行驶车辆的行驶距离。假设车速为v1=36 km/h 时，在第3 种行驶轨迹下得到最优纯电动汽车的计算结果，如图4 所示。

由图4a 可知，NSGA-II 优化算法刚开始运算时，分布离散，当进化至38 代时车道宽度为3.5 m 的加速度开始收敛形成pareto 最优解。当迭代次数一定时，随着车道宽度的增加，加速度变大；当车道宽度达到最大3.5 m 时，纯电动汽车加速度达到最大

3.999 m/s2。

由图4b 可知，NSGA-II 优化算法刚开始运算时，纯电动汽车多目标函数值分布离散，当进化至66 代时，纯电动汽车多目标函数值已无明显变化，只有个别车道宽度解集随着迭代次数的增加，优化结果逐渐收敛形成pareto 最优解。当车道宽度由小到最大时，纯电动汽车两目标优化结果逐渐变大，最大为9.66。

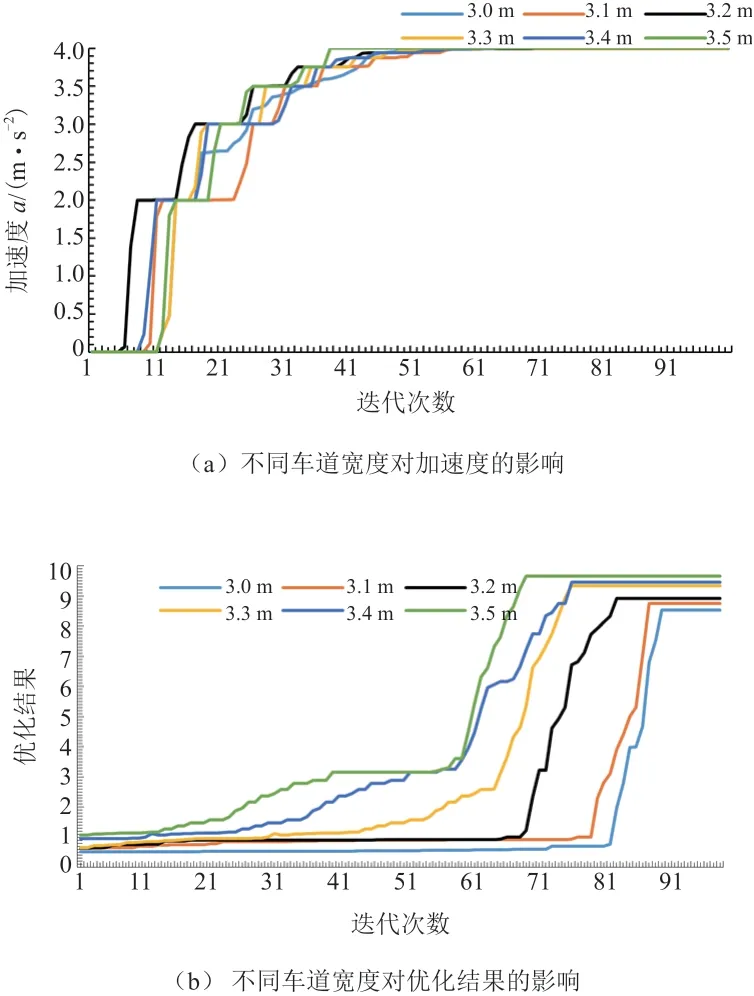
图4 不同单车道宽度的影响

结合表4 和表5 可知，当北进口左转车辆和南进口直行的纯电动汽车通过十字路口时，不同的车道宽度使纯电动汽车通过碰撞点的时间和距离都不一样，通过比较发现，车道宽度为3.0 ～3.5 m 时，直行的纯电动汽车通过碰撞点的时间和加速度变化很小。但由表4 可知，随着车道宽度的增加，左转车辆的行驶轨迹不变，直行的纯电动汽车行驶速度、加速度、总加权加速度均方根值以及优化结果同步增加，当车道宽度为3.5 m 时达到最大。所以，通过对比发现，当直行的纯电动汽车在车道宽为3.5 m行驶时，其安全性、经济性最好。

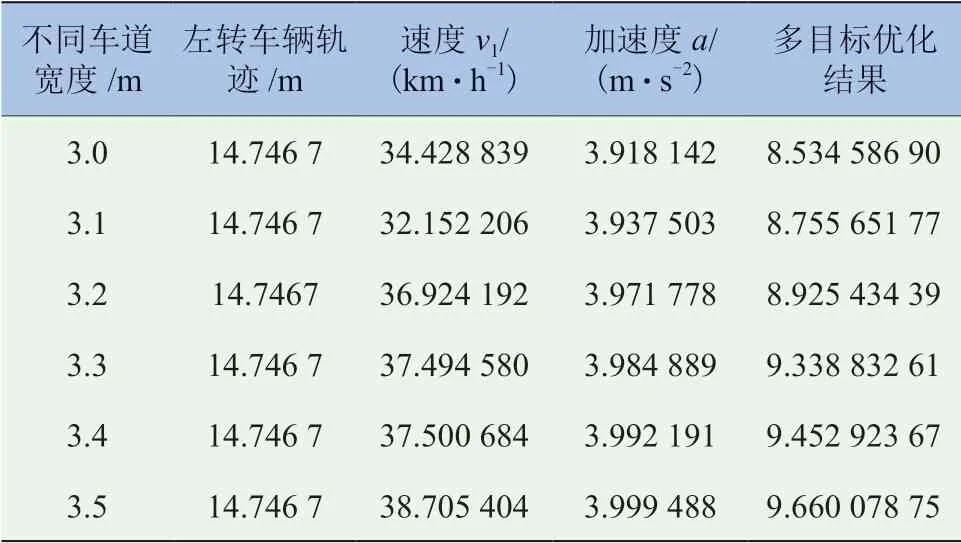
表4 不同单车道宽度的影响

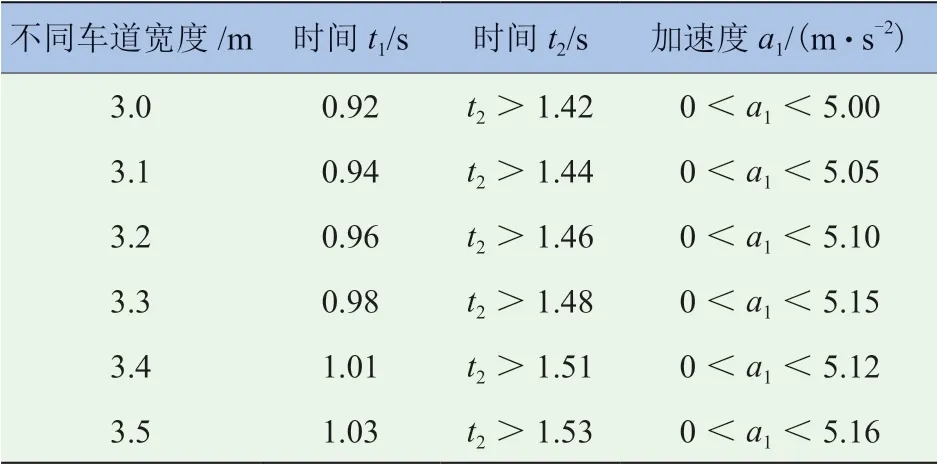
表5 直行的纯电动汽车安全通过十字路口

2.3 不同左转车速对纯电动汽车两目标函数的影响

左转车辆行驶速度发生变化会对到达碰撞点的时间产生影响，从而影响直行的纯电动汽车综合性能。由前两小节可知，当车辆行驶在第3 种轨迹且当单车道宽度n=3.5 m 时，纯电动汽车性能最优。因此，假设左转车辆以速度v1=18 km/h 和v2=36 km/h行驶，而其它条件不变的情况下，得到最优纯电动汽车的参数，见表6 和表7，计算结果如图5 所示。

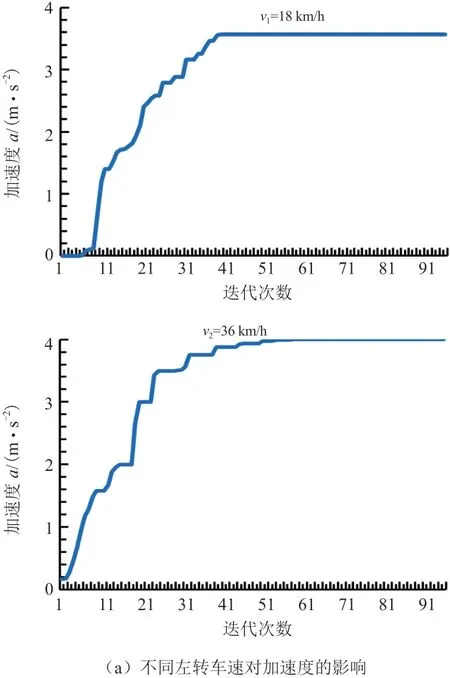
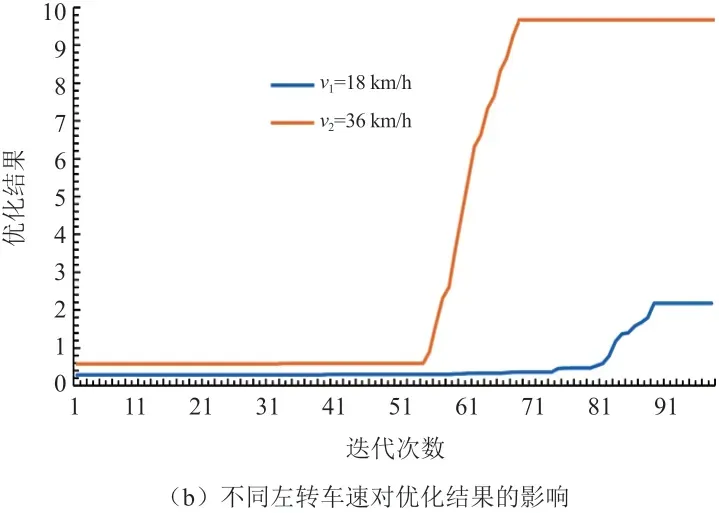
图5 不同左转车速的影响

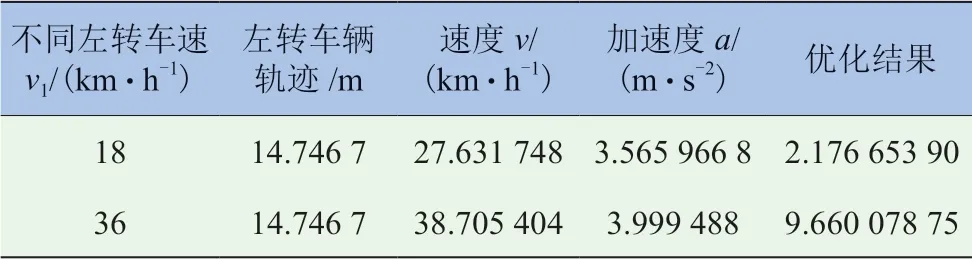
表6 不同左转车速的影响

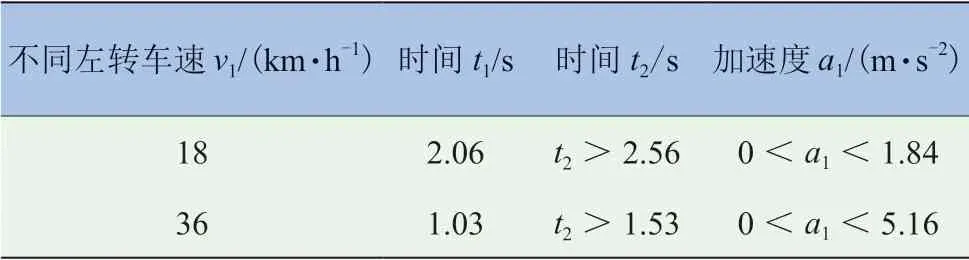
表7 直行的纯电动汽车安全通过十字路口

计算结果随着迭代次数的增加而相应变化。由图5a 可知，NSGA-II 优化算法刚开始运算时，分布离散，随着迭代次数的增加逐渐收敛，左转车速越快越先收敛。随着迭代次数的增加，加速度目标函数值无明显变化。当迭代次数一定时，随着左转车速的增加，纯电动汽车的加速度变大，当左转车速为36 km/h 时，纯电动汽车加速度达到最大，约为

3.999 m/s2。

由图5b 可知，刚开始运算时，纯电动汽车多目标函数值分布离散，当进化至68 代时，左转车速为v2=36 km/h 的纯电动汽车多目标函数值已无明显变化，形成pareto 最优解。当左转车辆的车速由小变大时，直行的纯电动汽车加速度逐渐变大，且逐渐收敛，当左转车速为36 km/h 时，其优化结果最大约为9.66，性能最好。

当北进口左转车辆和南进口直行的纯电动汽车通过十字路口时，不同的左转车速使北进口左转车辆到达碰撞点的时间发生变化，为了安全行驶从而会造成纯电动汽车通过碰撞点的时间和距离都不一样。由表6 可知，随着左转车辆速度的增加，直行的纯电动汽车行驶速度、加速度和优化结果同步增加，当左转车辆车速为36 km/h 时纯电动汽车的性能最好。由表7 可知，当左转车辆的车速为18 km/h 时，通过碰撞点的时间是车速为36 km/h 的两倍，且当左转车速过小时通过碰撞点的时间也较长，通过对比发现，随着左转车速的增加，直行的纯电动汽车加速性能越来越好。综上，随着左转车辆速度的增加，直行的纯电动汽车其安全性、经济性以及加速性能也越来越好，但在通过十字路口时其速度不能超过极限值40 km/h。

3 基于带精英策略遗传算法的车辆行驶控制

为了验证纯电动汽车两目标优化结果的准确性，并保证纯电动汽车通过十字路口安全行驶，本文设计了基于带精英策略遗传算法的纯电动汽车行驶控制方案。思路是首先利用传感器和车载摄像头采集信号和识别交通场景；然后将采集到的信息传递给控制部分；接着控制部分将获得的信息根据本文之前的多目标优化的条件和结果进行分析和预判；最后进行控制（加速、制动踏板）改变速度。本文的重点就是控制，所以在研究控制时假设前面的信号采集与场景识别系统已经完成。因此，考虑到控制的复杂性、行驶的非线性以及具备一定鲁棒性，所以采用模糊控制器。模糊控制器能很好地将车辆行驶过程中要实时获取的车速、加速度等信息进行融合，通过模糊推理分析后，达到纯电动汽车行驶控制，保证行车安全。控制系统原理如图6所示。

3.1 模糊控制原理

从1974 年产生至今，通过许多学者的不断研究，形成了极具代表性的Mamdani 型模糊控制器，如图7所示。所设计的模型参考控制思路主要是：

（1）利用摄像头识别道路交通场景并进行预判行驶轨迹，利用车载传感器采集纯电动汽车（被控对象） 的实际车速（控制变量y1）、实际加速度（控制变量y2）。

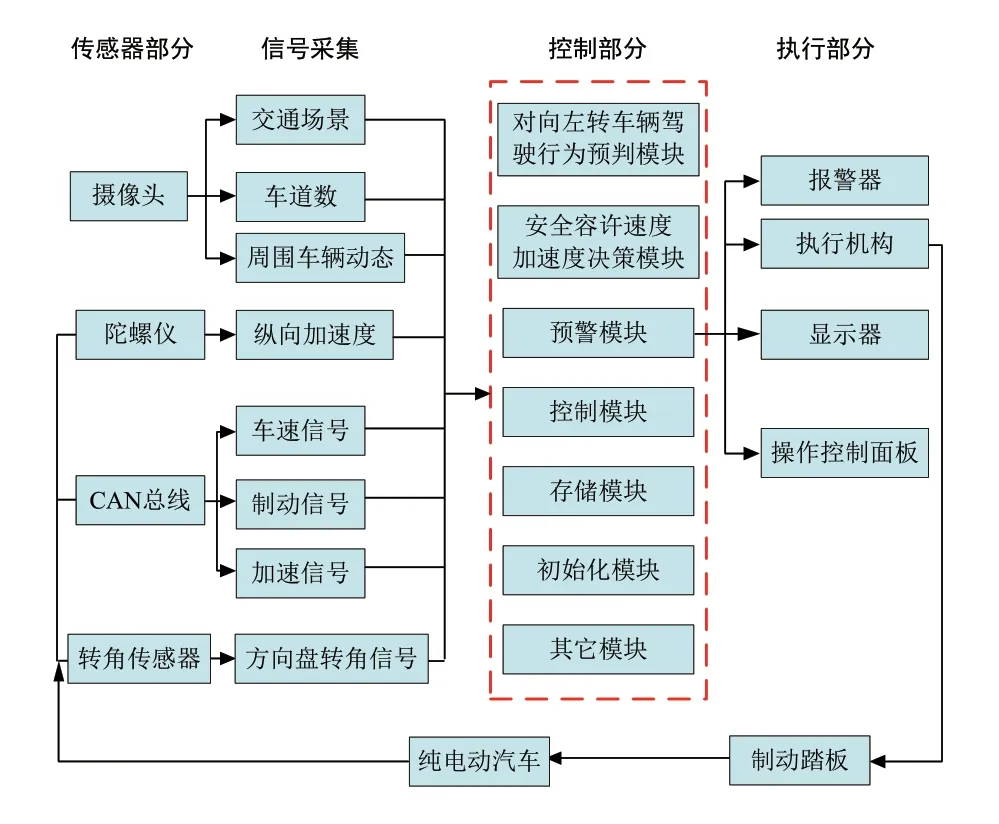
图6 控制系统结构原理

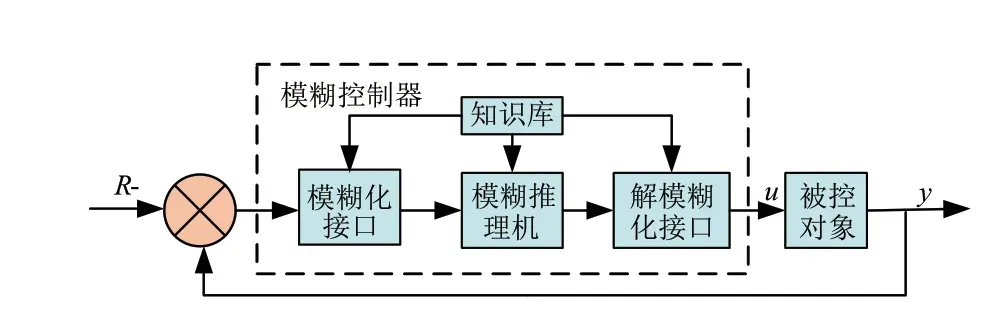
图7 模型参考模糊控制

（2）主要是利用容许目标车速R1、容许目标加速度R2减去实际车速y1、实际加速度y2，得到差值e，模糊化接口则将输入信号e模糊后得到模糊控制变量E，经过模糊控制规则处理得到信号u，则下层结构中的控制器响应，采取相应措施进行减速制动。

（3）利用得出的速度差值、加速度差值，结合之前得出的优化结果范围域对实际的车速、加速度进行调节，更好地满足纯电动汽车的安全、经济和舒适性研究。

3.2 模糊控制器设计

3.2.1 输入与输出变量

模糊控制器点的设计是控制系统最为重要的部分，由于约束变量主要是速度和加速度，因此，设计的模糊控制器是双变量输入、单变量输出的二维控制器，可以有效提高运算速度。假设e(vd)表示前面求出的容许目标车速R1与纯电动汽车实际车速y1的差值；e(a1)表示前面求出的容许目标加速度R2与纯电动汽车实际加速度y2的差值，即：

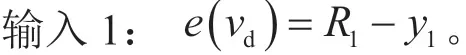
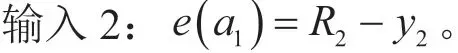
输出：以期望减速度U来衡量，在平直路段减速度范围为[-1.5，0]，单位为m/s2[12]。

3.2.2 模糊控制设计

模糊控制的确立主要是由模糊化、变量的模糊子集、模糊控制规则组成。

（1）模糊化

模糊语言数量越多，控制精度就越高，但模糊控制规则也随之增加，计算时间也相应增加。因此，本文输入变量采用5 个模糊语言数量。描述模糊变量e(vd)、e(a1)的模糊语言表述为：

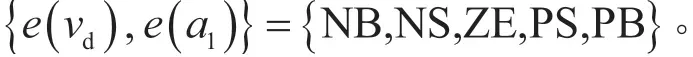
式中：NB 表示负大；NS 表示负小；ZE 表示零； PS 表示正小；PB 表示正大。

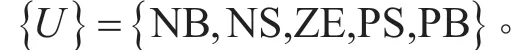
本文输出变量也采用5 个模糊语言数量。描述模糊变量期望减速度U的模糊语言表述为：式中：NB 表示负大；NS 表示负小；ZE 表示零； PS 表示正小；PB 表示正大。

（2）变量的模糊子集

隶属度函数就是变量的模糊子集，包括连续函数和离散函数两种形式，形状有Z 形、S 形、三角形、高斯型等。其中，隶属函数越陡其控制分辨率较高，灵敏度也增加。反之，灵敏度降低，控制系统更加稳定。因此，本文采用分辨率和灵敏度高的三角形隶属度函数。

（3）模糊控制规则建立

模糊规则表存在耗时少、生成简单、实用等优点，且速度输入e(vd)、加速度输入e(a1)各有5 个模糊控制语言，则生成25 条模糊控制规则，见表8。

3.3 模糊控制结果

根据以上纯电动汽车行驶速度、加速度模糊控制系统的建立，得到了如图8 所示的控制优化结果。

由图8a 的速度曲线可知，优化前的速度随着时间的增加，速度不是平稳增加，在3 s 的时候达到波峰（接近约束条件极大值40 km/h），之后一直以38.705 km/h 的速度稳态行驶，稳态精度较低。而采用了控制策略优化后的曲线稳定性能更好、稳态精度更高，不会出现速度波峰，在第3 s 后一直以38.705 km/h 的速度平稳行驶。由图8b 的加速度曲线可知，优化前的加速度随着时间的增加有波动，在3 s 的时候达到波峰（接近约束条件极大值4 m/s2），之后一直以3.999 m/s2的加速度稳态行驶，稳态精度较低。而采用了控制策略优化后的曲线稳定性能更好、稳态精度更高，不会出现加速度波峰，在第3 s 后一直以3.999 m/s2的加速度平稳行驶。

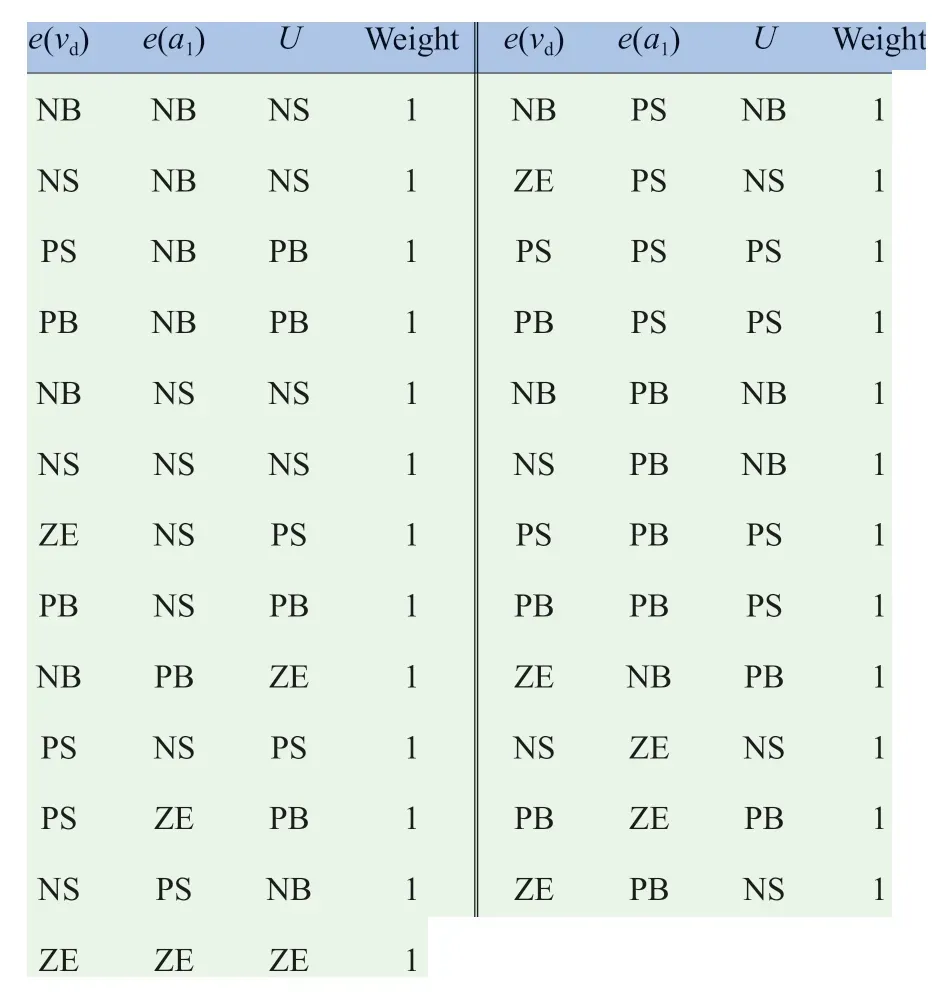
表8 模糊控制规则表

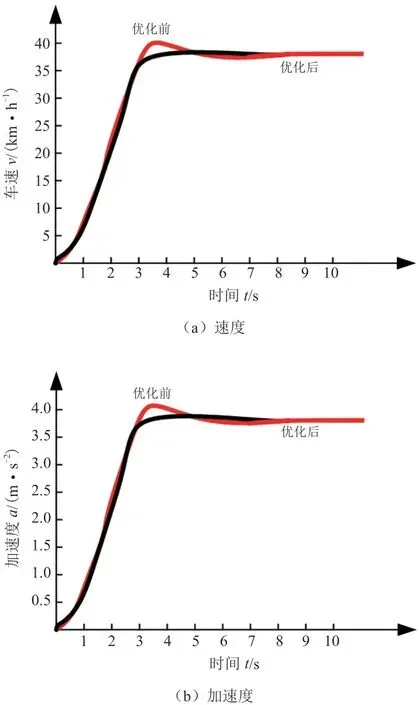
图8 纯电动汽车模糊控制结果

研究结果表明，优化后的速度、加速度的曲线更加平滑，不存在波峰或波谷，通过建立控制策略更能反映纯电动汽车操作稳定性更好，在通过十字路口时能平稳地控制车速，纯电动汽车的综合性能得到较大提高。

4 结论

（1） 研究表明，提出的基于NSGA-II 算法模糊控制策略和制定的相关隶属度函数、模糊规则，可以验证纯电动汽车多目标优化模型的准确性和可行性，操作稳定性更好，能够保障纯电动汽车较为平稳安全地通过十字路口。

（2） 基于城市干道工况，利用NSGA-II 遗传算法对纯电动汽车运行安全、节能两目标进行优化研究。结果表明，当纯电动汽车在双向4车道行驶时，在第3 种行驶轨迹、单车道宽为3.5 m、左转车辆行驶速度为36 km/h 的条件下，纯电动汽车安全性和经济性达到最优。该两目标函数很好地兼顾了纯电动汽车的安全、经济和加速性，提高了纯电动汽车的安全性和经济性。