基于内聚力模型的夹层玻璃冲击破坏仿真分析
李高杰,臧孟炎
(华南理工大学 机械与汽车工程学院,广州 510640)
近年来,我国汽车保有量持速增长,截止2018年9 月已达2.35 亿辆[1],与此同时,机动车交通事故也频繁发生。近年来,保护弱势道路使用者的生命安全受到各方重视,2018 年的中国新车评价规程新增了行人保护试验及评价,其中包括了非常重要的头部与汽车风挡玻璃之间的碰撞测试。为适应这一变化,精确高效的夹层玻璃冲击破坏仿真分析对于汽车被动安全设计至关重要。
内聚力模型最早用于模拟复合材料的分层过程[2]。后来,ORTIZ 等[3]将其应用于模拟陶瓷的脆性断裂,JIN Guanglai 等[4]采用双线性内聚力模型研究了沥青混凝土劈裂疲劳试验,常晓林等[5]使用内聚力模型研究了不同粉煤灰掺量和不同孔隙率对混凝土细观力学参数和开裂的影响。LI Dejia 等[6]和GAO Wei 等[7]使用内聚力模型模拟了汽车风挡玻璃在假人头冲击下的断裂行为,并进行了参数化研究。张其林等[8]建立了考虑大位移非线性效应的夹层玻璃有限元模型,研究了夹层玻璃在风载作用下的响应。LIU Bohan 等[9]进行了一系列头模块与风挡玻璃的参数化冲击试验,并仿真分析了PVB在能量吸收中的作用。综上所述,使用内聚力模型模拟陶瓷、玻璃等材料的脆性断裂可以弥补基于连续体的有限元方法在分析脆性破坏时遇到的挑战。但是,着眼于工程应用的需要,有必要深入研究夹层玻璃的有限单元类型和有限元网格分布对仿真分析精度和仿真计算效率的影响。
本文在介绍内聚力模型基本原理的基础上,建立了夹层玻璃板落锤冲击破坏试验有限元模型,采用有限元商用软件ABAQUS 实施仿真分析。在确认仿真分析模型的有效性之后,研究了夹层玻璃有限单元类型和网格分布形式对仿真精度和计算效率的影响。其中,有限单元类型包括六面体单元、五面体单元以及六面体和五面体混合单元,网格分布形式包括以冲击点为中心的辐射状网格分布和单元尺寸大小一致的均匀状网格分布,为行人保护评价的有限元仿真分析工程应用提供指导和帮助。
1 内聚力模型
商用有限元软件ABAQUS 和LS-DYNA 均嵌入了双线性内聚力模型[10],其本构关系如图1 所示。图1 中OA 线段表示内聚力单元的线弹性阶段,A 点表示内聚力单元的损伤起始点,AB 线段表示了内聚力单元的损伤演化阶段分别代表当变形完全垂直于内聚力单元分离界面或完全在第一或第二剪切方向时的名义应力峰值,与之对应的界面分离位移量分别为3 个方向上的失效界面分离位移量和临界断裂能分别为
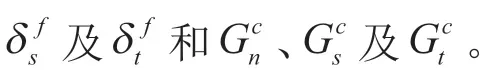
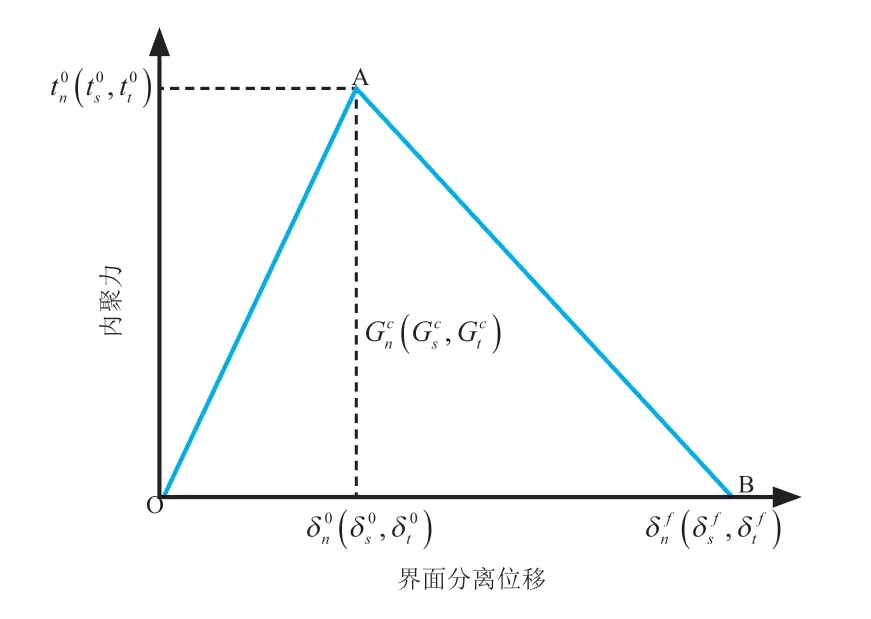
图1 双线性内聚力模型本构关系
名义牵引应力矢量t由3 个方向上的分量组成:tn、ts及tt,相应的分离量用δn、δs及δt表示,用T0表示内聚力单元的初始厚度,名义应变可以表示为:
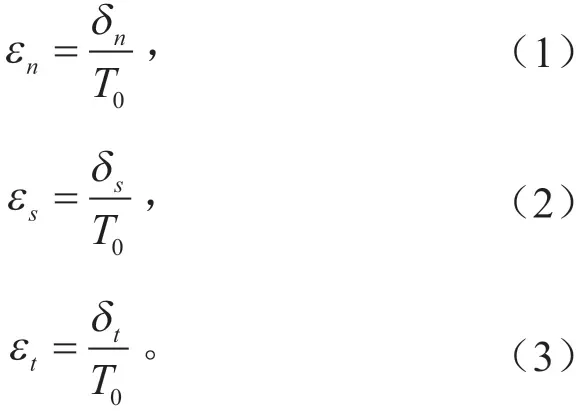
内聚力单元的弹性行为如式(4)所示。使用式(5)所示的最大名义应力准则判断内聚力单元是否达到损伤起始点。

损伤演化规律描述了内聚力单元达到损伤起始点后刚度退化的速率,如式(7) ~(9)所示。
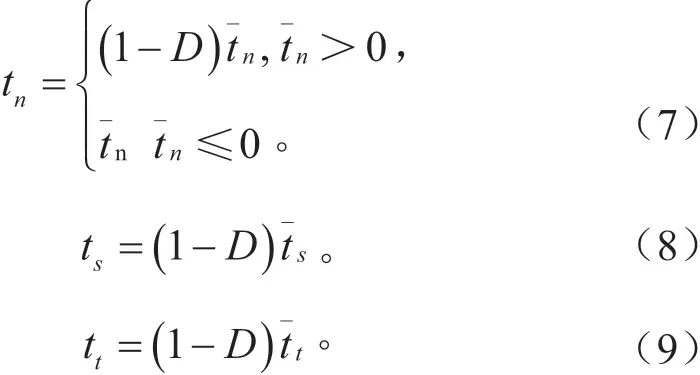
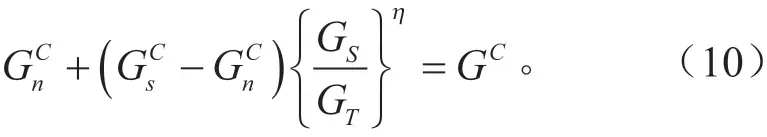
内聚力模型通过插入相邻有限单元界面的内聚单元,表达破坏的发生和裂纹的传播。与图1 所示的本构关系相对应的内聚单元为固有内聚单元,它们在建立有限元仿真模型时就已经嵌入。还有一种内聚单元叫非固有内聚单元,在仿真计算过程中根据需要插入。本文基于固有内聚单元,研究夹层玻璃冲击破坏现象。
2 夹层玻璃冲击破坏仿真分析与评价
基于夹层玻璃落球冲击试验[12],考虑结构与载荷的对称性,建立如图2 所示的1/4 对称有限元模型a。采用六面体单元在冲击点中心附近划分辐射状网格,远离冲击点区域采用尺寸较大的均匀网格。上层玻璃划分五层网格,下层玻璃划分三层网格,中间PVB 为一层网格。通过编写Fortran 程序,读取玻璃的单元与节点信息,根据内聚力单元(COH3D8、COH3D6)的几何结构特征,直接在所有玻璃单元的公共界面之间定义零厚度内聚力单元,按照ABAQUS 规定的格式输出到原inp 文件中,并用内聚力单元来模拟玻璃的破坏。冲击破坏试验有限元模型中的落锤和橡胶支撑垫均采用六面体单元。
夹层玻璃冲击破坏仿真分析中,由于玻璃单元不发生破坏,将玻璃单元选择为弹性材料模型。内聚力单元的材料参数为玻璃材料的强度及断裂能等参数,罚刚度取500 GPa/mm。落锤视为刚体,PVB与橡胶支撑垫均采用超弹性材料模型(Mooney-Rivlin)。模型中各部件的材料模型及材料参数见表1[12-14]。落锤位于夹层玻璃中心正上方,初速度为6.7 m/s。在夹层玻璃落锤冲击破坏试验中,玻璃与PVB 没有出现分层现象,因此将PVB 与上下层玻璃对应的节点进行绑定约束(tie)。橡胶支撑垫与夹层玻璃下表面接触,对橡胶支撑垫的下表面节点实施全自由度约束,对模型施加对称边界条件约束。落锤与玻璃的接触及橡胶垫与玻璃的接触均采用ABAQUS 中的一般接触(general contact),摩擦因子均为0.1。
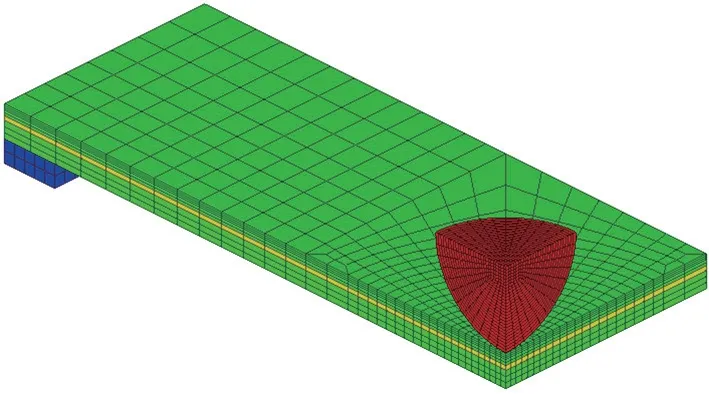
图2 夹层玻璃冲击破坏试验有限元模型a
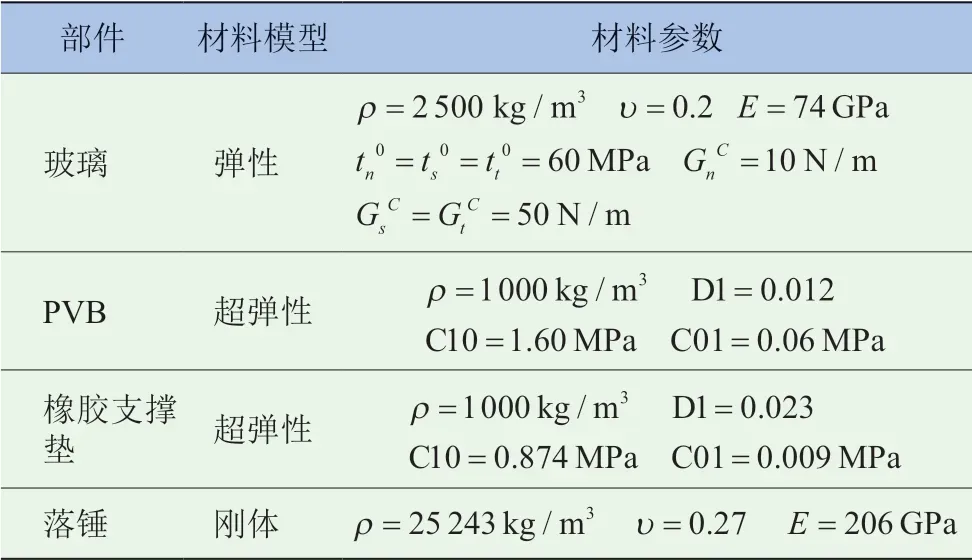
表1 材料模型及材料参数
使用ABAQUS/Explicit 进行求解,计算得到的落锤加速度时间历程曲线与玻璃裂纹分别如图3 和图4 所示。图3 中的仿真加速度峰值为16 224.88 m/s2,与试验峰值15 663.34 m/s2的相对误差为3.59 %,且加速度时间历程曲线与试验结果整体吻合良好。图4 中的夹层玻璃的破坏模式与试验结果基本一致,冲击中心区域出现粉碎性破坏,径向裂纹从中心区域出发向四周扩展,环向裂纹以中心区域为圆心。仿真与试验结果的一致性验证了仿真模型的有效性。

图3 模型a 与试验加速度时间历程曲线

图4 破坏模式仿真与试验结果对比
3 有限元模型影响因素分析
3.1 有限单元类型的影响分析
ABAQUS 软件中,除六面体单元外,五面体单元也可以使用内聚力模型。为讨论有限单元类型对仿真分析结果的影响,分别建立了图5 所示的夹层玻璃板辐射状五面体单元、辐射状六面体与五面体混合单元有限元模型b 和c,它们的最小单元尺寸与图2 中模型a 的最小单元相同。除单元类型的定义不同外,有限元模型的其余定义均与模型a 一致。

图5 夹层玻璃板网格模型b-c
将模型a、模型b 和模型c 的仿真分析结果归纳至图6 和图7。由图6 可知,模型a 的落锤加速度时间历程曲线与试验结果的一致性最好,模型b和模型c 的一致性不如模型a。比较图4 和图7 的玻璃破坏模式,模型a 和模型c 与试验结果最接近,模型b 与试验结果相差最大。此外,从表2 所示的3 个模型CPU 计算时间可知,模型a 最小,模型b所需时间是模型a 的3 倍多,模型c 的计算时间接近模型a 的两倍。
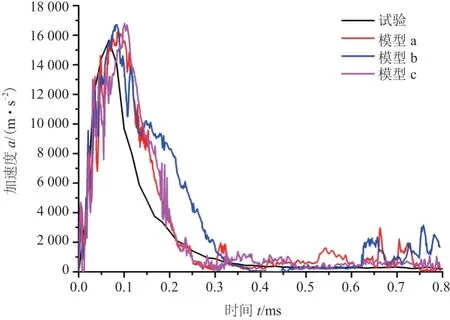
图6 模型a、b、c 与试验加速度时间历程曲线
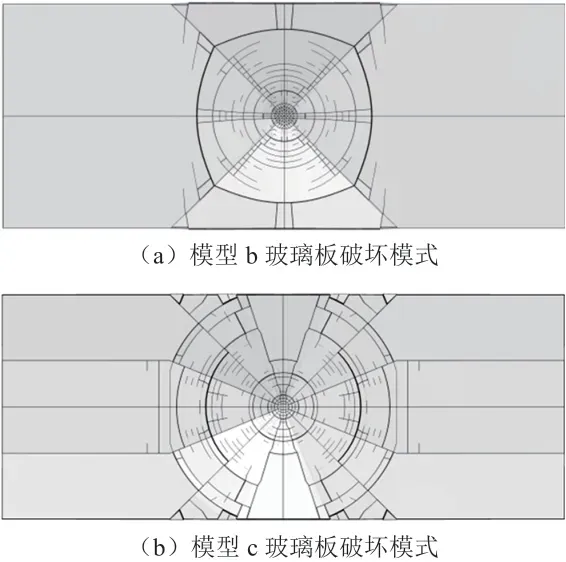
图7 模型b、c 玻璃板破坏模式
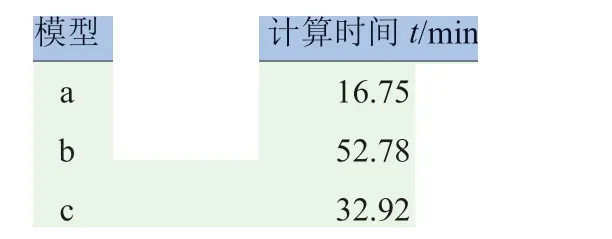
表2 模型a、b、c 的CPU 计算时间
因此,不同单元类型对仿真精度和计算效率有较大影响。六面体单元的仿真精度和计算效率最高;五面体单元在可接受的范围内;而六面体和五面体混合单元的仿真精度和计算效率在六面体单元和五面体单元之间。这种混合单元在工程应用中具有重要意义,因为汽车前挡玻璃自动网格划分时容易出现六面体和五面体混合单元有限元模型。
3.2 有限元网格分布的影响分析
由上节的分析可知,六面体单元的仿真精度和计算效率都是最高的,因此,本节采用六面体单元研究网格分布的影响。考虑辐射状(图2)和不同尺寸均匀分布(图8)两种形式的网格,模型d 的玻璃单元数量与模型a 基本一致,模型e 的玻璃单元尺寸与模型a 的最小单元尺寸相同。其它条件的定义均与模型a 一致。

图8 夹层玻璃板网格模型d、e
由图9 所示的落锤加速度时间历程曲线可知,模型a 的加速度时间历程曲线与试验结果的一致性最好,模型d 的加速度峰值明显高于试验值,模型e的加速度时间历程曲线与试验结果对应良好,但一致性程度低于模型a。由图4 及图10 的裂纹图可知,模型a 的裂纹与试验结果对应最好,而模型d、e 的裂纹与试验结果差别巨大,径向和环向裂纹不显著。此外,从表2 及表3 的CPU 计算时间中可以看出,模型a、d 的计算时间均在20 min 之内,而模型e由于单元尺寸过小导致单元数量过多,计算时间达到了模型a 的近10 倍。

表3 模型d、e CPU 计算时间
综上所述,均匀分布六面体网格构成的夹层玻璃冲击破坏仿真模型,难以得到与试验对应的破坏模式。随着均匀网格尺寸的减小,冲击加速度仿真曲线与试验一致性提高。但是,辐射状分布网格的仿真精度和计算效率都很好。
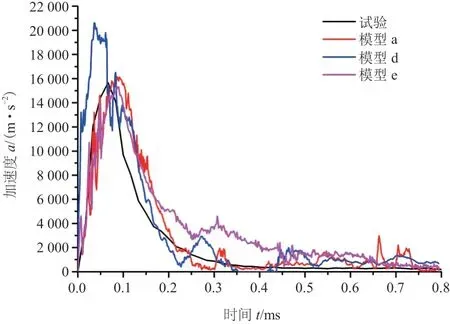
图9 模型a、d、e 与试验加速度时间历程曲线

图10 模型d、e 玻璃板破坏模式
4 结论
建立了5 种不同类型的夹层玻璃冲击破坏有限元模型,以冲击加速度和破坏模式为评价标准,考虑CPU 计算时间的影响,得出以下结论。
(1)在商业有限元软件ABAQUS 中建立了基于内聚力模型的夹层玻璃冲击破坏有限元模型,仿真得到的玻璃板裂纹及落锤加速度时间历程曲线与试验结果一致性良好,验证了仿真方法及模型的有效性。
(2)由于五面体单元的计算精度低于六面体单元,夹层玻璃冲击破坏有限元模型应该尽可能采用六面体单元。以六面体单元为主的六面体和五面体混合单元有限元模型,也可以得到比较满意的计算结果。
(3)尽管网格划分复杂程度稍高,但无论在仿真分析精度,还是在仿真计算效率方面,以冲击点为中心的辐射状网格分布是夹层玻璃冲击破坏有限元分析模型的理想网格分布方式。

