低维半结合3-代数的分类
白瑞蒲,刘培,张艳
(河北大学 数学与信息科学学院,河北 保定 071002)
3-元代数系统在数学和物理的很多领域都有着广泛的应用.例如,3-李代数[1-2]就与Nambu力学系统及可积系统有着非常紧密的关系[3-5],在膜理论中,著名的Bagger-Lambert 模型的建立就基于度量3-李代数的结构[6-7].3-李代数是非结合代数,它与3-Pre-李代数、李代数、结合代数等都有着紧密的联系.文献[8]构造了一类半结合3-代数,并且由半结合3-代数构造出了3-李代数.本文要继续研究有限维半结合3-代数的结构,并对低维半结合3-代数进行分类.
1 预备知识
在下面的讨论中,假设F是特征为0的域.
定义1[8]设A是定义在域F上的向量空间,如果A上的3-元线性运算{,,}:A⊗A⊗A→A对于任意xi∈A(1≤i≤5),满足式(1)-(3),则称A为半结合3-代数,
{x1,x2,x3}=-{x2,x1,x3},
(1)
{x1,{x2,x3,x4},x5}={x1,x2,{x3,x4,x5}},
(2)
{x1,{x2,x3,x4},x5}={x5,{x2,x3,x4},x1}+{x1,{x5,x3,x4},x2}.
(3)
假设B1、B2、B3是A的子代数,由所有向量{x1,x2,x3}生成的A的子空间记为{B1,B2,B3},其中xi∈Bi,i=1,2,3.子代数A1={A,A,A}称为A的导代数,若A1=0,则A称为Abel的.
定义2[8]若半结合3-代数A的子空间B满足条件{B,B,B}⊆B,B称为A的子代数.若B满足{A,A,B}⊆B和{A,B,A}⊆B,则B称之为A的理想.
显然,{0}和A都是A的理想,称为平凡理想.如果A没有非平凡理想,则称A为单纯半结合3-代数.
设V是半结合3-代数A的子空间,子代数
ZA(V)={x|x∈A,{x,V,A}={V,A,x}=0}
(4)
称为V的中心化子.ZA(A)称为A的中心,并且简记为Z(A),即
Z(A)={x|x∈A,{x,A,A}={A,A,x}=0},
(5)
显然Z(A)是A的一个理想.
引理1[8]设A是半结合3-代数.
如果A中存在非零向量e1、e2、e3、e4使得{e1,e2,e3}=e4,则e4≠λes,其中λ∈F,λ≠0,s=1,2,3.
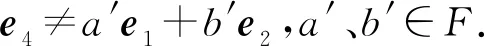
引理2[8]设A是非-Abel的半结合3-代数,并且dimA=m≥3,则A中存在线性无关的向量ei、ej、ek使得{ei,ej,ek}≠0.
引理3[8]设A是s-维的半结合3-代数,并且s≤6,则A1⊆Z(A).
2 低维半结合3-代数的分类
定理1A是半结合3-代数并且dimA≤2,则A是Abel的,即{A,A,A}=0.
证明:可由引理1直接得出.
定理2假设A是3-维半结合3-代数,e1、e2、e3是A的一组基,则在同构的意义下,仅有如下2种情形:
1) {A,A,A}=0.
2) {e2,e1,e1}=e3,其中e1、e2、e3是A的一组基.
证明:如果A是非-Abel的,那么根据引理2,存在A的一组基e1、e2、e3使得{e1,e2,e3}≠0.假设{e1,e2,e3}=ae1+be2+ce3≠0,a、b、c∈F.根据引理1,c≠0,并且a≠0或b≠0,不妨假设a≠0并且a=1,对基e1、e2、e3做线性变换:用e1+be2替换e1,可得{e1,e2,e3}=e1+ce3,c∈F,c≠0根据式(1)、式(2)和引理2,可知
{e1,e2,e2}={{e1,e2,e3}-ce3,e2,e2}=c{e2,e3,e2}-{e2,{e1,e2,e3},e2}=
c{e2,e3,e2}+{e2,e2,{e1,e3.e2}}=c{e2,e3,e2},
(6)
{e1-ce3,A,A}={A,A,e1-ce3}=0,
(7)
{e1,e2,e1}={e1,e2,{e1,e2,e3}-ce3}=-c(e1+ce3).
(8)
对基e1、e2、e3用c(e1+ce3)替换e3做线性变换,得到{e3,A,A}={A,A,e3}=0,{e2,e1,e1}=e3.
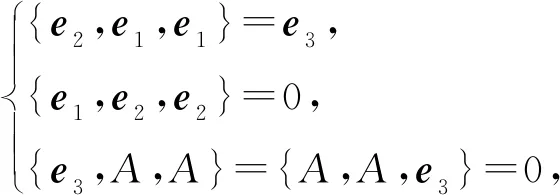
得到情形2).
若{e1,e2,e2}≠0,并假设{e1,e2,e2}=a1e1+b1e2+c1e3.根据式(2)和引理2,
{e1,{e1,e2,e2},e2}=b1{e1,e2,e2}=0,
(9)
{e2,{e1,e2,e2},e1}=-{e2,e2,{e1,e2,e1}}=0=a1{e2,e1,e1}=a1e3,
(10)
得到a1=b1=0并且{e1,e2,e2}=c1e3,c1≠0.得到情形2).证毕.
定理3A是4-维半结合3-代数,e1、e2、e3、e4是A的一组基,则在同构的意义下,A是下列情形之一:
1) {A,A,A}=0.
2) {e1,e4,e1}=e3.
证明:若A是非-Abel的,根据引理3,可知dimZ(A)≤2.
当dimZ(A)=2时,假设e2、e3是Z(A)的一组基.因为{A,A,A}≠0,再由引理2可得{A,A,A}⊆Z(A),并且存在e1、e4∈A使得{e1,e4,e1}≠0或{e1,e4,e4}≠0.因为e1、e2、e3、e4是A的一组基,不失一般性,假设{e1,e4,e1}≠0,则{e1,e4,e1}=a1e1+b1e2+c1e3,{e1,e4,e4}=a2e1+b2e2+c2e3,其中ai、bi、ci∈F,i=1,2.根据式(2),
(11)
可得a1=a2=0,{e1,e4,e1}=b1e2+c1e3≠0,{e1,e4,e4}=b2e2+c2e3.
如果dimA1=1,假设{e1,e4,e1}=e3,则{e1,e4,e4}=c2e3.用e4-c2e1代替e4,得到情形2).
如果dimA1=2,可知导代数A1中的{e1,e4,e1}和{e1,e4,e4}线性无关,因此,可以假设{e1,e4,e1}=e3,并且{e1,e4,e4}=e2.得到情形3).
当dimZ(A)=1时,根据文献[8]的定理2.8和{A,A,A}≠0,dimA1=1以及A1=Z(A),设非零e3∈Z(A),则{A,A,A}=Fe3.根据引理2可知A中存在线性无关的3个向量e1、e2、e4使得{e1,e2,e4}≠0.因此e1、e2、e3、e4是A中一组基,可以假设{e1,e2,e4}=e3得到
(12)
从dimZ(A)=1和式(2)可知e4∉Z(A),c5=c8=0,得到情形4).
由于dimZ(A)=1,所以情形4)不同构于情形2)和3).因为导代数维数不同,可得情形3)不同构于情形2).证毕.
定理4A是5-维半结合3-代数,e1、e2、e3、e4、e5是A的一组基,则在同构的意义下,A是下列情形之一:
1) {A,A,A}=0.
2) {e1,e4,e1}=e3.

证明:若A是非-Abel的,根据引理3,可知dimZ(A)≤3.
当dimZ(A)=3时,假设e2、e3、e5是Z(A)的一组基.根据引理3以及{A,A,A}≠0可知存在e1、e4∈A,使得{e1,e4,e1}≠0或{e1,e4,e4}≠0.因e1、e2、e3、e4、e5是A的一组基,不失一般性可假设{e1,e4,e1}≠0,并且
{e1,e4,e1}=a1e1+b1e2+c1e3+f1e5,{e1,e4,e4}=a2e1+b2e2+c2e3+f2e5,
(13)
其中ai、bi、ci、fi∈F,i=1,2.根据式(2),
可得a1=a2=0并且
{e1,e4,e1}=b1e2+c1e3+f1e5≠0,{e1,e4,e4}=b2e2+c2e3+f2e5.
(14)
如果dimA1=1,根据式(14),可假设{e1,e4,e1}=e3,{e1,e4,e4}=c2e3.用e4-c2e1代替e4,得到情形2).
如果dimA1=2,由式(14)可知导代数A1的{e1,e4,e1}和{e1,e4,e4}线性无关,因此可假设{e1,e4,e1}=e3,并且{e1,e4,e4}=e5.得到情形3).
当dimZ(A)=2时,设e3、e5∈Z(A)线性无关.根据引理2以及引理3可得{A,A,A}⊆Z(A),则存在线性无关的向量e1、e2、e4∈A-Z(A)使得e1、e2、e3、e4、e5是A的一组基,并且A在这组基下的乘法表为
(15)
如果dimA1=1,根据式(15),fi=0,3≤i≤10.因此A=B+Fe5,其中B是A的4-维子代数,e1、e2、e3、e4是B的一组基,并满足dimB1=dimZ(B)=1,得到4).
如果dimA1=2,根据引理1,式(2)和式(15),假设{e1,e4,e4}=e5,再用e2-f10e1代替e2,式(15)简化为
(16)
对于∀e=ae1+be2+de4∈A,如果{A,e,A}={A,A,e}=0,根据式(16),
{e2,e,e4}={e2,ae1+be2+de4,e4}=(-a+dc10)e3=0,
{e1,e,e4}={e1,ae1+be2+de4,e4}=be3+de5=0.
(17)
因此a=b=d=0.可得乘法表为式(16)的半结合3-代数,满足dimZ(A)=2时是情形5).
当dimZ(A)=1时,设非零e3∈Z(A),则Z(A)=Fe3.根据引理1和引理2,可知A-Z(A)中存在线性无关的4个向量e1、e2、e4、e5使得{e1,e2,e4}=e3,{e1,e2,e5}=0.因此e1、e2、e3、e4、e5是A中一组基,并且A在这组基下的乘法表为
设B是以e1、e2、e3、e4为基的A的子代数.对于任意非零向量e=ae1+be2+de4∈A,如果{e,B,B}={B,B,e}=0,则e=dc22e1-dc21+de4,并且c21=c22=0.
在情形4)和5)中dimZ(A)=2,在情形6)中dimZ(A)=1,所以情形2)和3)不同构于情形4)、5)和6).因为在情形3)中dimA1=2,所以情形2)不同构于3).同理情形5)不同构于4).结论证毕.
3 结语
对2、 3、 4、 5-维的半结合3-代数的结构进行了分类,证明了2-维半结合-3-代数是Abel代数,在同构的意义下,仅存在2类3-维半结合-3-代数,其乘法结构如定理2所述,4类非同构的4-维半结合-3-代数及6类非同构的5-维半结合-3-代数,且在一组基的乘法表分别如定理3和定理4所述.
——以指数、对数函数同构问题为例

