新型非常规U型转弯交叉口的运行效率研究

潘兵宏，单慧敏，任 卉，胡 炜

1) 长安大学公路学院，陕西西安 710064；2)长安大学特殊地区公路工程教育部重点试验室，陕西西安 710064

平面交叉口(以下简称交叉口)左转车辆的存在会大幅增加交叉口的拥堵，为更好地解决交叉口直接左转车辆带来的冲突问题，研究人员提出了各种措施．彭飞等[1]通过考虑延误和排队等因素建立交叉口信号配时优化模型． SHAIK等[2]建立左转车道仿真模型，给出单左转车道和双左转车道的适用条件．张野等[3]提出在交叉口的出口道设置左转专用可变车道的交通组织方法．KOEPKE等[4-6]分别提出U型、扇形、菱形及左转漂移等新型交叉口设计．其中，交通组织优化仍然是解决该问题的重要途径．为消除左转对交叉口处的不利影响，研究人员设计了各类左转方式．利用左转目标道路的中央分隔带开口和相邻交叉口，通过右转加掉头的方式来实现左转也是常用的交叉口左转组织措施，此方式被称为U型转弯．U型转弯可显著减少交叉口冲突以及车辆的平均延误，提高交叉口的通行能力[7]．但常规利用中央分隔带的U型转弯要求中央分隔带具有足够的宽度(典型的利用中分带U型转弯交叉口，如密歇根U型转弯，宽度一般要超过18 m[8])，以满足左转车辆掉头要求，这限制了该方法的应用．对于中央分隔带非常狭窄的道路，很难设计成常规U型转弯来实现车辆左转．此外，在有大量左转交通且中央分隔带较窄的地方，若要设计成常规U型转弯，需考虑小型车和大型车转弯对行驶车辆的影响．本研究提出一种新型非常规U型转弯(new unconventional U-turn intersection， NUUT)设计，即分车道分车型的双湾U型转弯交叉口，以放宽对道路中央分隔带宽度的要求．

1 NUUT几何结构分析

NUUT的几何结构如图1，本研究考虑NUUT的应用环境为城市道路．从安全行车和保障效率两方面考虑，路段中用于掉头的中央分隔带开口前，必须设置专用左转车道．在常规U型转弯交叉口的基础上，对主干路上游路段局部拓展出两条专用掉头车道(内侧为小型车，外侧为大型车)，避免大小车型转弯时的冲突，有利大型车转弯．同时采用逐级渐变的方式，达到减少车道浪费，避免排队长度过长的目的．大车在靠近中央分隔带的第2条车道转至对向车道，可更好的满足U型转弯车辆所需要的转弯半径，减少大型车掉头对同向直行车造成的延误．尽管NUUT仍对中央分隔带宽度有要求，但比常规的U型转弯设计要求要窄得多．

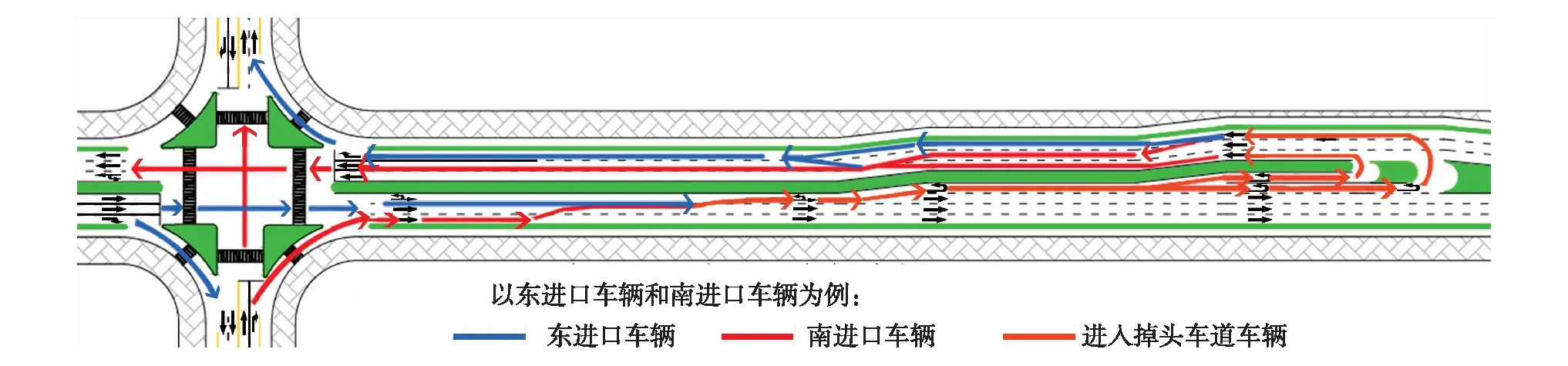
图1 新型非常规U型交叉口(NUUT)示意图Fig.1 New unconventional U-turn diagram for intersection

本研究拟针对不同交通情况下， NUUT的延误、停车次数和排队长度3个指标，分析车辆左转对交叉口的影响，评估NUUT的运行效率．

NUUT适用于常规交叉口，评估时预设条件为：① 该交叉口禁左，且至下游信控交叉口的距离满足长度要求，可在路段中间设置开口，既能保证交织完成，也能保证信控交叉口正常运行；② 交叉口与上、下游的邻近信控交叉口之间无其他出入口接入．《城市道路工程设计规范》(CJJ37—2012)[9]规定主干路的设计速度为40～60 km/h，次干路的设计速度为30～50 km/h，交叉口内的右转弯设计速度宜为路段的0.5～0.7倍，车道宽度均取3.5 m，主干路至少为双向6车道，次干路取双向4车道．

2 NUUT模型建立

2.1 交通变量

NUUT主要交通变量如图2．其中，i=1, 2, 3, 4， 分别为东南西北4个进口方向；o为车辆在交叉口处目标行驶方向，o=1, 2, 3, 4, 5， 分别为左转、直行、右转、在U型转弯处转弯以及U型转弯处的交织车辆；a为进入交叉口处车道的编号，从最内侧算起；nia为某一方向进口道车道数；e为交叉口出口处车道的编号；nie在某一方向出口道车道数；N为目标路段车道数．

图2 交通变量分布示意图Fig.2 Transportation variable distribution diagram

交叉口处每个方向的进口交通流量Qi(i=1, 2, 3, 4)是该方向目标行驶交通流量之和，即

(1)

进口方向i(i=1, 2, 3, 4)的左转弯比例为

(2)

以东进口方向为例，掉头混合车道交通流量为

(3)

i方向(i=1, 2, 3, 4)各进口道a的交通量为

(4)

2.2 几何尺寸

2.2.1 掉头位置与交叉口之间的间距L

为防掉头车辆过多，在交叉口处溢出，L应大于进入交叉口处的排队长度[10]，即

(5)

其中，tio为在交叉口的某一方向中车辆行驶方向的绿灯时间(单位：s)；C为信号周期时长(单位：s)；s为车头间距(单位：m)．

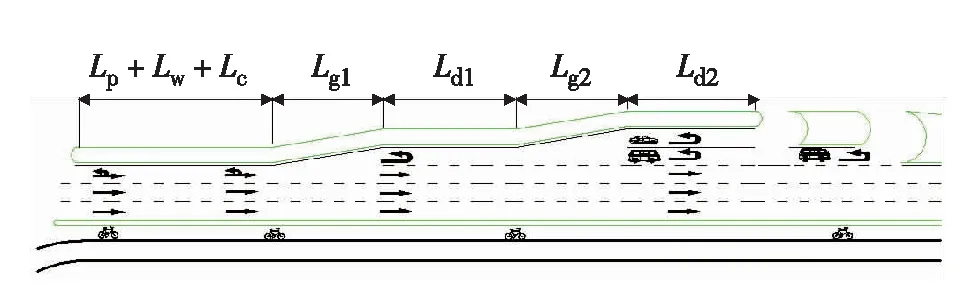
图3 开口间距L计算示意图Fig.3 Open space L calculation diagram

在实际应用中若无可计算L的基础参数，可采用图3的开口间距计算模型．其中，Lp为感知反应距离；Lw为换道所需的等待可插入间隙的距离；Lc为车辆横移距离；Lg1和Lg2为大型车和小型车专用车道的展宽渐变段长度；Ld1和Ld2分别为展宽等待段的要求长度．由图3可知，L应满足车辆换道至最内侧车道所需距离Lp+Lw+Lc、Lg1、Lg2、Ld1和Ld2的要求.

1)换道至最内侧车道所需距离Lp+Lw+Lc：为尽量让掉头车辆在第1次渐变段前进入最内侧车道以减少对直行车辆的影响，该段距离应满足Lp、Lw[11]及Lc各自的要求，如式(6)至式(9)．

(6)

其中，tp为感知反应时间，本研究根据文献[12]设tp=2.5 s；v为次干路车辆在进入主干路后车辆需要连续换道进入内侧车道时的运行速度(单位：km/h)．为保证足够的距离和行车安全，在计算感知反应距离时，v取本研究中次干路的设计速度40 km/h．

(7)

其中，v1为等待可插入间隙期间车辆的运行速度(单位：km/h)，取主干路设计速度的70%，本研究中主干路速度取50 km/h；tw为等待一个可插入间隙的时间，计算式为

(8)

其中，λ为单位时间内的平均到达率(单位：pcu/s)，λ=Q/3 600，Q为最大服务交通量(单位：pcu/h)，根据《城市道路工程设计规范》(CJJ 37—2012)，本研究取Q=1 350 pcu/h；tc为车辆临界间隙，取值3.5～4.0 s，本研究取4.0 s；τ为最小车头时距，取值为1.0～1.5 s，本研究取1.2 s[11]．

Lc为横移换道距离，计算式为

(9)

其中，tc为换道时间，取tc=3 s；v2为主干路设计速度(单位：km/h)．

经计算，当主干路为双向6车道，次干路为双向4车道时，换道距离为Lp+2Lw+2Lc=156 m．

美国国家高速公路和交通运输协会(American Association of State Highway and Transportation Officials, AASHTO)建议交叉口和掉头位置之间的最小间距取值为122～183 m．因此，本研究计算的距离与AASHTO建议距离基本一致．

2)展宽渐变段长度Lg和展宽段长度Ld：NUUT通过逐级渐变方式，拓宽出两条专用的左转车道．由于中国现阶段并无对应的规范，本研究参照《城市道路交叉口设计规程》相关规定，令主干路展宽渐变段Lg1=Lg2=30 m，展宽段长度Ld1=70 m，Ld2=42 m，则小车L=328 m．

2.2.2 掉头处中央分隔带的最小宽度

满足小客车和大型车掉头的中央分隔带的宽度分别为5.3～6.4 m和7.7～9.4 m[13]．远引车辆在中央分隔带处掉头时，车辆的行驶轨迹半径与车辆的大小和内外轮转角等有关，小客车和大型车的转弯半径R分别取4 m和9 m[12]．远引掉头处的主路中央分隔带的宽度E应满足

E≥2R-NWL-2Wb

(10)

其中，WL为跨越的车道宽度；Wb为路缘带宽度，根据《城市道路路线设计规范》要求， 本研究取WL=3.50 m， 取Wb=0.25 m．

由式(10)计算得到，当中央分隔带的最小宽度为4 m时，小客车可直接掉头到对向车道第1条车道(靠近中间带)上．大客车可直接掉头至最外侧行车道．

3 仿真环境设定

采用Vissim交通流仿真系统对NUUT运行效率进行仿真分析．以双向6车道和双向4车道为研究对象，研究不同的交通情况下NUUT和直接左转交叉口(direct left turn, DLT)、无专用车道U型转弯(U-turn, UT)以及有1条拓宽车道的U转弯(one lane U-turn, OLUT)设计的差异．

本研究根据道路自身条件及输出结果比较的需要，提供不同预设交通量，并在仿真前对模型进行校准，使结果更接近实际情况[14-15]．为得到稳定交通流，每次仿真时间定为3 600 s，而对应每一水平、每一因素都平行地进行8次仿真试验[16]．VISSIM仿真模型的输入参数为：

1)通过现场实际观察多个城市道路交叉口，大车比例占1%～8%，本研究取2%～10%，以2%的梯度增加.

2)主路单向交通量为800～2 100 veh/h，次干路上单向交通量为100～1 100 veh/h，梯度均为100 veh/h，次干路交通量要低于主干路交通量．

3)由于U型转弯对主干道直行需求较高，左转需求较低，因此本研究假定左转、直行和右转的交通量之比为0.3∶0.5∶0.2．

4)根据文献[10]的调查结果，小客车的转弯速度为12.3 km/h，行驶速度为7.1～18.7 km/h；大型车的转弯速度为9.7 km/h，行驶速度为 7.2～10.8 km/h．

5)东西路的车辆初始速度为50 km/h(大部分车辆的行驶速度为48～58 km/h)，南北路的车辆速度为40 km/h(大部分车辆的行驶速度为40～45 km/h)．

4 运行评价指标对比分析

4.1 NUUT与DLT对比分析

为说明NUUT的适用交通量范围，本研究将其与DLT在设定的仿真环境下进行对比．将假定的交通参数输入到仿真模型中，其中大型车比例固定为2%，只改变交通量的取值．根据道路交通参数利用交通信号配时软件SYCHRO计算出DLT的最佳信号配时．

4.1.1 路网平均延误对比

不同交通情况下NUUT较DLT的路网平均延误降低率D如式(11)，仿真对比结果如图4．

(11)

其中，dNUUT与dDLT分别为NUUT与DLT的延误．

图4 NUUT与DLT路网平均延误降低率Fig.4 Average delay reduction rate on NUUT and DLT network

在给定的交通组成中，红色区域为NUUT适用的最佳交通量范围，适用的次干路交通量最高达到800 veh/h，并在之后逐渐降低．在主、次干路交通量组合为(2 100, 100)veh/h时，平均延误超过2 min时适用性较小，则主干路交通量超过2 100 veh/h时不再作为适用交通量考虑．

仿真结果表明，在适用的交通量范围内路网的平均延误为2.20～117.32 s，降低了5.64%～85.73%．其中，主、次干路交通量组合为(1 900, 200)veh/h时延误降低最小，主、次干路交通量组合为(900, 100)veh/h时延误降低最大．当主干路或次干路交通量不断增加时，车辆延迟将急剧增加，并且交叉口变的非常拥挤．图4中仅红色部分NUUT对DLT的改善效果明显，其余部分远超相同交通量组合下DLT的车辆延误，延误增长了5.69%～495.84%．当主干路交通量小于1 800 veh/h，且不能改善DLT时，对U型转弯处进行信号控制．在次干路为700 veh/h和900 veh/h车辆延误将降低到DLT以下．次干路交通量为1 100 veh/h或主干路交通量超过1 800 veh/h，信号控制不再能够解决此时车辆拥堵的问题．

4.1.2 停车次数对比

不同交通情况下NUUT较DLT的路网平均停车次数降低的百分率S如式(12)，仿真对比结果如图5．

(12)

其中，sNUUT与sDLT分别为NUUT和DLT的停车次数．

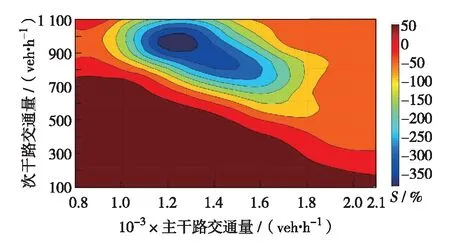
图5 NUUT与DLT路网平均停车次数降低率Fig.5 Average reduction rate of number of stops on NUUT and DLT network

与路网平均延误类似，随着主干路交通量的增加，适用的次干路交通量逐渐降低，NUUT适用的次干路交通量最高约达800 veh/h．

由仿真结果可知，在适用的交通量范围内路网的平均停车次数为0.03～2.24次，降幅6.17%～94.22%．延误降低率的最小值和最大值对应的主、次干路交通量组合分别为(1 600, 500)veh/h和(800, 100)veh/h．

4.1.3 排队长度对比

不同交通情况下NUUT较DLT的路网平均排队长度降低的百分率Lq如式(13)，仿真对比结果如图6．

(13)

其中，lq, NUUT与lq, DLT分别为NUUT和DLT的平均排队长度．

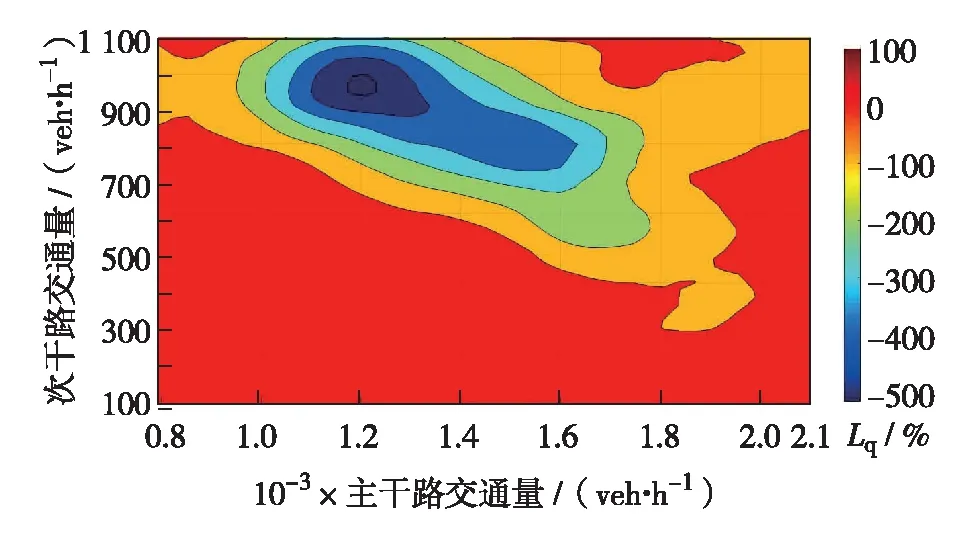
图6 NUUT与DLT路网平均排队长度降低率Fig.6 Average reduction rate of queue length on NUUT and DLT network

分析排队长度发现，NUUT所适用的交通量范围要较路网平均延误和平均停车次数两个指标更广．在给定的交通组成中，仅红色部分NUUT能够改善DLT的运行性能．在适用的交通量范围排队长度降低了6.44%～95.38%．主干路交通量为1 400 veh/h，次干路交通量为600 veh/h时延误降低最小，主干路交通量为900 veh/h，次干路交通量为100 veh/h时延误降低最大．

综合上述3种指标[17]，NUUT比DLT具有更好的改善交叉路口运行性能的潜力．NUUT适用的主干路交通量所对应的最大次干路交通量(以主干路双向6车道，次干路双向4车道为例)，如表1．

表1 NUUT适用的交通量

Table 1 Traffic volume applicable to NUUT veh/h

4.2 NUUT与U型转弯交叉口不同车辆组成下运行特点比较

通过分析NUUT与DLT的运行效率指标，得到NUUT适用的交通量组合，并在此基础上进一步研究大型车比例变化情况下NUUT与U型转弯交叉口(UT和OLUT)之间的差异.NUUT的几何结构如图1，U型转弯交叉口的小客车掉头位置与NUUT一致.

通过对比NUUT与DLT的路网平均延误、车辆平均停车次数和路网车辆的平均排队长度，发现它们的变化规律类似．其中，路网的平均延误包含平均行程时间延误、平均停车延误和平均排队延误等，在一定程度上反应了车辆的总体运行特点．因此，以下仅针对路网平均延误进行分析．

4.2.1 NUUT与UT不同车辆组成下运行特点比较

对NUUT与UT在不同车辆组成(大型车比例分别占2%、4%、6%、8%和10%)条件下进行仿真对比，结果发现，在给定的交通量组成下，NUUT能明显降低路网延误，而在不同交通组成情况下，NUUT与UT的路网平均延误规律类似．限于篇幅，本研究仅给出在大型车比例为8%时的图示，见图7，其他车辆组成条件下的路网延误降低率图示请扫描论文末页右下角二维码见图S1．

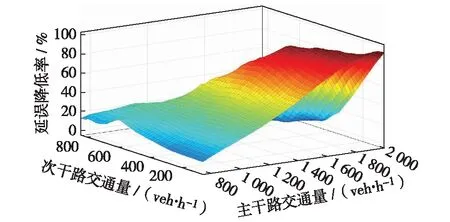
图7 NUUT与UT路网平均延误降低率 (大型车比例8%)Fig.7 Average delay reduction rate on NUUT and UT network (the ratio of heavy vehicles is 8%)

分析大型车比例变化的5种情形下延误指标．在相同大型车比例下，随着主干路和次干路交通量的增加，NUUT路网的平均延误始终小于UT的．路网延误的降低率增到最大值后增幅变缓．

在主干路交通量增加到一定值时，路网延误降低率呈大范围高值．路网平均延误降低率达到80%以上时，随着大型车比例增大，所适用的主干路交通量范围变小．NUUT比UT的路网延误降低了1.45%～98.00%.主次干路交通量组合为(800，300)veh/h且大型车比例为2%时延误降低率最小；主次干路交通量组合为(1 700, 300)veh/h且大型车比例为8%时延误降低率最大．

4.2.2 NUUT与OLUT不同车辆组成下的运行特点比较

当道路上掉头车辆较多时，许多道路会拓宽出1条专用掉头车道．通过仿真得到NUUT较OLUT的路网平均延误降低率，同样仅给出大型车比例为8%时的图示，如图8，其他车辆组成情况下NUUT和OLUT路网的平均延误降低率图示请扫描论文末页右下角二维码见图S2．

图8 NUUT比OLUT路网的平均延误降低率 (大型车比例8%)Fig.8 Average delay reduction rate on NUUT and OLUT network (the ratio of heavy vehicles is 8%)

同NUUT与UT的运行效率对比类似，除大型车比例为2%时的个别交通量组成，NUUT路网的平均延误总是低于OLUT的．路网延误的降低率逐渐增加，达到最大值时，路网延误降低率开始减少．

对比NUUT与OLUT，二者的路网延误降低率范围为0.30%～97.97%．主次干路交通量组合为(1 000， 700) veh/h，且大型车比例为2%时延误降低率最小；主次干路交通量组合为(1 800， 200) veh/h，且大型车比例为8%时延误降低率最大．

4.2.3 NUUT与UT对比最佳运行效率组合

以NUUT与DLT运行特点对比下的最佳交通量为基础，进一步对比在不同大型车比例下NUUT的运行效率做．结果发现，不同大型车比例下所适用的次干路交通量相近．取其均值并对运行效率最佳时的交通量按照式(14)进行多项式线性拟合，结果如图9．

图9 运行效率最佳交通量Fig.9 Corresponding traffic volume when operating efficiency is optimal

g(x)=-0.527 2x+1 196

(14)

其中，x为主干路交通量，x≥800 veh/h；g(x)为NUUT与U型交叉口对比下最佳次干路交通量．

式(14)中自变量系数的95%置信区间为(-0.614 8, -0.439 5)，截距的95%置信区间为(1 069, 1 323)，二者在统计学上都显著，且拟合度R2=0.940 9， 说明该方程能解释95%的变异，拟合度较好．

NUUT交通量组合位于g(x)下方时呈最佳运行效率．最佳交通量组合的变化规律为：随主干路交通量的增加，次干路交通量逐渐降低．当位交通量组合位于g(x)上方时，NUUT将不再适用．

以上分析表明，NUUT与U型交叉口的对比所适用的最大交通量呈线性分布，随着主干路交通量的增加，次干路交通量渐降．同时，NUUT设计能有效提高不同交通量、不同大型车比例情况下的路网运行效率．

5 实例验证

对中国西安市西部大道与博士路交叉口进行调查，交叉口东西方向为双向8车道，南段为双向4车道，北段进口道为3车道，出口道为2车道．小车转弯速度为(12, 42)km/h，大车转弯速度为(11, 37)km/h．交叉口交通量及信号配时如表2和表3．

表2 交叉口交通量Table 2 Traffic volume of crossing veh/h

表3 交叉口信号配时(周期T=141 s)Table 3 Signal timing at intersections (T=141 s) s

基于采集到的基本参数，分别建立DLT、UT、OLUT和NUUT的仿真模型，并对比4种交叉口的路网平均时间．利用SYCHRO对U型转弯重新配时，得到周期为56 s，中央分隔带开口位置距交叉口210 m．为保证获取的样本数量为大子样，改变随机种子，对每个模型仿真50次．取置信水平为95%，对交叉口母体平均值μ1m和μ2进行假设检验分析，结果如表4．

表4 样本延误统计分析表Table 4 Statistical analysis of sample delays

(15)

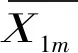
对延误的样本平均值进行大子样条件下的U检验，得到样本平均值满足

(16)

此时，U检验结果落在拒绝域内，即拒绝H0，接受H1．因此，当α=5%时，NUUT的平均延误要小于DLT、UT和OLUT，表明NUUT设计的运行效率要更优．

实际交叉路口的中央分隔带为14.0 m通过改建成NUUT的形式使道路两侧分别缩减1.5 m．对于UT和OLUT保持道路建筑红线不变，中央分隔带宽度分别取4.0 m和14.0 m时，比NUUT的道路用地更大且运行效率更低．

结 论

1)为降低常规U型交叉口对中央分隔带宽度的要求，提出一种新型非常规U型交叉口(NUUT)，并设置相关几何参数．NUUT解决了大小车转弯半径的冲突、车道浪费以及排队长度过长等问题．同时，NUUT不必设计较宽的中央分隔带，减少空间浪费．

2)利用Vissim软件进行仿真，通过比较NUUT与DLT的运行指标，得出NUUT适用的交通量组合．NUUT的设计使路网平均延误降低了5.64%～85.73%，停车次数降低了6.17%～94.22%，排队长度降低了6.44%～95.38%，有效提高了路网的运行效率．

3)在适用的交通量范围及不同的车辆组成条件下，比较NUUT、UT和OLUT的运行特点，发现NUUT能够更好的改善道路运行效率，当道路大型车比例增加时，运行效率改善效果更好．

4)将NUUT应用到实际交叉口，与DLT、UT和OLUT交叉口设计相比，NUUT有效减少了交叉口延误和建筑用地．

但是，本研究仅将交叉口置于一个孤立的点，下一步可基于周边路网来更精确地评估NUUT的运行效率．