不平衡标记差异性多标记特征选择算法

王一宾，吴 陈，程玉胜，江健生

1)安庆师范大学计算机与信息院，安徽安庆 246133；2)安徽省高校智能感知与计算重点实验室，安徽安庆 246133

现实世界广泛存在着多标记学习对象，多标记学习已日渐成为机器学习、数据挖掘和深度学习[1-2]等领域的研究热点之一．这些标记之间并非相互独立的，而是有着一定的关联，如一篇新闻报道可能同时属于“经济”、“体育”和“国家”；人的面部表情可能同时被“开心”、“激动”和“兴奋”等标记．因此，如何利用标记的相关性构造出泛化性较强的分类器是多标记学习的关键之一[3]．刘军煜等[4]通过挖掘标记之间的关联性，提出一种关联规则挖掘的多标记分类算法．何志芬等[5]提出基于多标记分类和标记相关性的联合学习．蔡亚萍等[6]利用标记的局部相关性进行多标记学习和分类．吴磊等[7]通过构建标记的类属属性提出基于类属属性的多标记学习算法．王一宾等[8]通过关联规则分析标记空间并提出一种基于回归核极限学习机的多标记分类算法．例如，在某个实例中，是否有该标记与实例的特征属性密切相关，如“感冒”和“肺炎”都有“发烧”和“咳嗽”症状，但若还有“流鼻涕”症状，则“感冒”的可能性要大于“肺炎”，此现象被称为标记的不平衡性．标记的不平衡性广泛存在于现实世界中，也正是由于标记的不平衡性造成了不同标记对样本实例的描述程度存在一定的差异性，有些标记出现的频率较多，能描述大部分的样本；而有些标记仅仅存在于少量样本中，但往往这一小部分的标记却包含了很多信息．可见，实例的特征会直接影响到标记的结果，因此，研究特征与标记的相关性十分重要．

传统处理不平衡性标记的方法大多是先通过抽样或重采样将不平衡数据处理为平衡数据再进行研究，但是这种方式常会改变原数据集属性，丢失部分信息，降低分类器的分类精度．若能将不同标记包含的信息加入到分类过程中，则不仅能保留特征空间的原始属性，还能提高分类器的精度．在多标记学习中，为更准确的描述样本实例，往往需要大量特征，且特征越多描述越准确．但随着特征数据的增加，弱相关特征和冗余特征也增多，严重影响到分类器的分类精度，甚至造成误分类．因此，需先对特征数据进行降维．特征选择是一种广泛使用且有效的降维方法，经过解析样本特征与标记之间的相关性，选择出相关性高且冗余性小的特征作为特征子集进行分类训练与预测[9]．张振海等[10]提出一类基于信息熵的多标记特征选择算法．刘景华等[11]基于互信息提出基于局部子空间的特征选择算法．LIN等[12-13]通过扩展互信息提出一种基于邻域互信息的多标记特征选择算法，进而又提出一种基于模糊互信息的特征选择算法．

研究发现，在多标记学习中，由于标记对样本的描述存在差异性，即在每个标记下正类与负类出现的频率不一样，这种标记频率分布可为多标记学习的研究提供一定的辅助信息，从而提高分类的精度[14]．本研究提出一种不平衡标记差异性多标记特征选择(multi-label feature selection algorithm with imbalance label otherness, MSIO)算法，首先计算标记空间中，记录每个标记下正标记(正类)样本和负标记(负类)样本出现的频率分布，并作为相应标记的权值保存在权值矩阵中；其次，考虑到标记空间中的标记包含一些辅助信息结合信息熵设计相应的度量方法以度量特征与标记之间的相关性；最后，根据所构造出的模型提出不平衡标记差异性多标记特征选择算法．在11个常用公开数据集上与5个常用的多标记特征选择算法[15]对比，证明MSIO算法可提高分类器的分类精度．

1 相关知识

1.1 多标记学习框架

多标记学习是一种针对实际生活中普遍存在的多义性现象的学习框架，在此框架下，样本由多个特征和多个标记构成，学习目的是将未知的实例对应上更多正确的标记[16]．

假设T是由n个特征组成的特征集合T={t1,t2, …,tn}，L是由m个标记组成的标记集合L={l1,l2, …,lm}， 在标记集合中，有该标记为1，否则为0，则含有z个样本的多标记数据集表示为

DataSet={(Ti,Li)|1≤i≤z,Ti∈T，Li∈L}

(1)

1.2 信息熵与互信息

定义1[11]若X={x1,x2, …,xm}为随机变量，xi的概率为p(xi)， 则X的不确定性期望为

(2)

H(X)亦被称为随机变量X的熵，其值越小表示X的期望和不确定性程度越小．

定义2[11]设随机变量X={x1,x2, …,xm}和Y={y1,y2, …,yn}， 则X和Y的联合熵为

(3)

定义3[11]设随机变量X={x1,x2, …,xm}，Y={y1,y2, …,yn}， 则Y在X条件下的条件熵为

(4)

H(Y|X)可用来度量Y在给定X时的不确定性程度．

定义4[11]若X和Y为已给定的随机变量，则定义X与Y之间的互信息为

(5)

I(X;Y)用于衡量随机变量X和Y的相关性，I(X;Y)越大，表明X与Y之间的相关性越大．同时，互信息还满足以下关系

I(X;Y)=H(X)+H(Y)-H(X,Y)=

H(X)-H(X|Y)=

H(Y)-H(Y|X)

(6)

2 不平衡标记差异性多标记特征选择

2.1 特征与标记集合的互信息

在多标记学习中，一个样本由多个特征和标记描述，则特征与标记集合之间的互信息可定义为：

定义5[11]对于给定描述样本的特征f和标记集合L={l1,l2, …,lm}， ∀li∈L，i=1, 2,…,m， 若特征f与标记li之间的互信息为I(f;li)， 则特征f与标记集合L之间的互信息为

(7)

由I(f;li)≥0可知， IML(f;L)≥0． 当f和L相互独立时，等号成立，此时特征与标记之间不提供任何信息，即该特征与标记空间互信息为最小值． 互信息值越大， 特征与标记之间的关系越密切．

同理，式(8)和式(9)成立．

IML(f;L)=IML(L;f)

(8)

(9)

根据式(9)可得，若

(10)

则表明标记集合L可完全由特征f确定，两者的不确定度之和取得最大值．

2.2 不平衡标记差异性多标记特征选择模型

在多标记数据集中，常因标记的不平衡性导致不同标记对样本描述程度有所不同，而目前多数算法并未考虑这种情况．为此，本研究根据标记空间中的每个标记下的正负样本个数对标记赋予权值，建立标记权值模型，具体定义为：

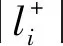
对于传统的单标记运用互信息进行特征选择过程中，假使用两个特征f1和f2对样本进行刻画，则对于特征与特征之间的冗余性用I(f1;f2)进行有效表示；倘若样本的特征用给定的f表示，样本的类别标记用l表示，则对于特征与标记类别之间的相关程度用I(f;l)进行有效表示．而在现有的多标记学习中，各个样本可用1个特征向量来表示，也可能隶属于多个类别标记，同时，充分考虑到标记权值模型下的各样本所含有的有用信息，因此需对加权特征和标记集合之间的相关性进行更深层次的探究.定义7给出了加权特征与标记集合之间的互信息定义.

定义7对于给定样本空间U={x1,x2,…,xz}， 标记空间L={l1,l2, …,lm}， ∀li∈L，i=1,2,…,m, 由定义6和式(7)可知，加权特征f与标记之间的互信息为

(11)

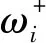
2.3 MSIO算法描述

考虑到标记对样本的描述存在一定的差异性，为使描述的样本实例更准确，同时也为了更充分地挖掘存在于少量样本中但包含众多有用信息的一些标记，首先计算标记空间中同一标记下正负标记的权值；其次，利用加权信息熵度量特征与标记空间之间的相关性，并由此得出两组不同的特征重要度排序；最后，将两组重要度不同的特征进行融合排序，得出最终特征序列．MSIO算法伪代码如图1．

输入:多标记训练集D输出:排序后的特征序列rank1) IML=⌀;2)for each fi∈F3) rank=⌀4) for each lj∈L5) 根据定义5计算和IML(fi; L+j)和IML(fi; L-j)6) end7) 根据式(11)计算每个特征fi在同一标记的不同情况下的互信息8)end9)根据7)得到的互信息降序排序,得到正标记的特征序列rank+和负标记的特征序列rank-10)对rank+和rank-融合排序,得到最终序列rank,并输出

图1 MSIO算法伪代码

Fig.1 Pseudocode of MSIO algorithm

分析图1的算法可见，MSIO算法先通过统计标记空间中类标记下的正负标记密度，然后计算标记空间与特征空间的相关性，并按照标记密度对特征进行赋权得分输出两组序列，再按照一定关系对两组序列加权得出最终序列．此方法简单易行且运行快速，既考虑了多种因素，又能有效提高分类器的分类精度．MSIO算法流程图如图2．

3 实验数据及结果分析

3.1 实验数据

采用Mulan数据库[16]中11个常用的公开实验数据集 (表1)，来验证算法MSIO的有效性．

3.2 评价指标

利用平均准确率(average precision, AP)、排位损失(ranking loss, RL)、1-错误(one-error, OE)和海明损失(Hamming loss, HL) 4个评价指标[18]对多标记实验实验结果进行验证和评价度量．

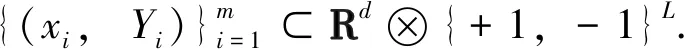
AP为评估预测标记排在前列且正确存在于相关样本标记的平均概率，如式(12)．该值越大表示分类效果越好，最优值为1．

(12)

其中，Yi为隶属于样本xi的相关标记集合．

RL用于评估无关标记在相关标记的样本前列的多少，如式(13)．该值越小表示分类效果越好，最优值为0．

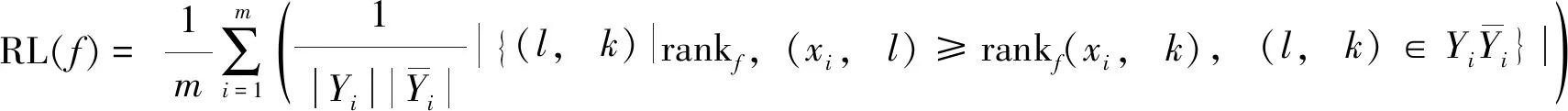
(13)

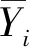
HL用于衡量样本在单一标记上的非正确匹配情况，如式(14)．该值越小，分类效果越好，最优值为0．

(14)

其中，Yi为隶属于xi的相关标记集合；h(·)为分类器，即可得xi的预测标记向量．

OE用于衡量最高排序中样本的标记不存在于相关标记集合中的情况，如式(15)．该值越小，表示分类效果越好，最优值为0．

(15)

在4个评价指标中，除去AP值越大越优，其余的越小越优．

3.3 实验结果及分析

本研究实验代码均在Matlab2016a中运行，硬件环境Inter®CoreTMi7-7700HQ CPU @ 2.80 GHz，8 Gbyte内存；操作系统为Windows 10．以多标记k近邻(multi-labelk-nearest neighbor, ML-kNN)[19]作为基础分类器，对基于最大相关性的多标记维数约简(multi-label dimensionality reduction via dependence maximization, MDDM)算法[20-21]、基于多变量互信息的多标记特征选择算法PMU(pairwise multivariate mutual information)[22]、 多标记朴素贝叶斯分类的特征选择(feature selection for multi-label naive Bayes classification, MLNB)算法[23]、 基于标记相关性的多标记特征选择(multi-label feature selection with label correlation, MUCO)算法[13]和MSIO算法的AP、RL、OE和HL值进行排序．其中，MDDM算法按照参数所选择的不同分为MDDMspc与MDDMproj算法．由于MDDM、PMU、MUCO和MSIO算法得到的是一组特征序列，于是设置特征子集的个数与MLNB算法一致，并设ML-kNN中的平滑系数s=1， 近邻个数k=10． 表2至表5列举了6种算法在数据集中的AP、RL、OE和HL值．

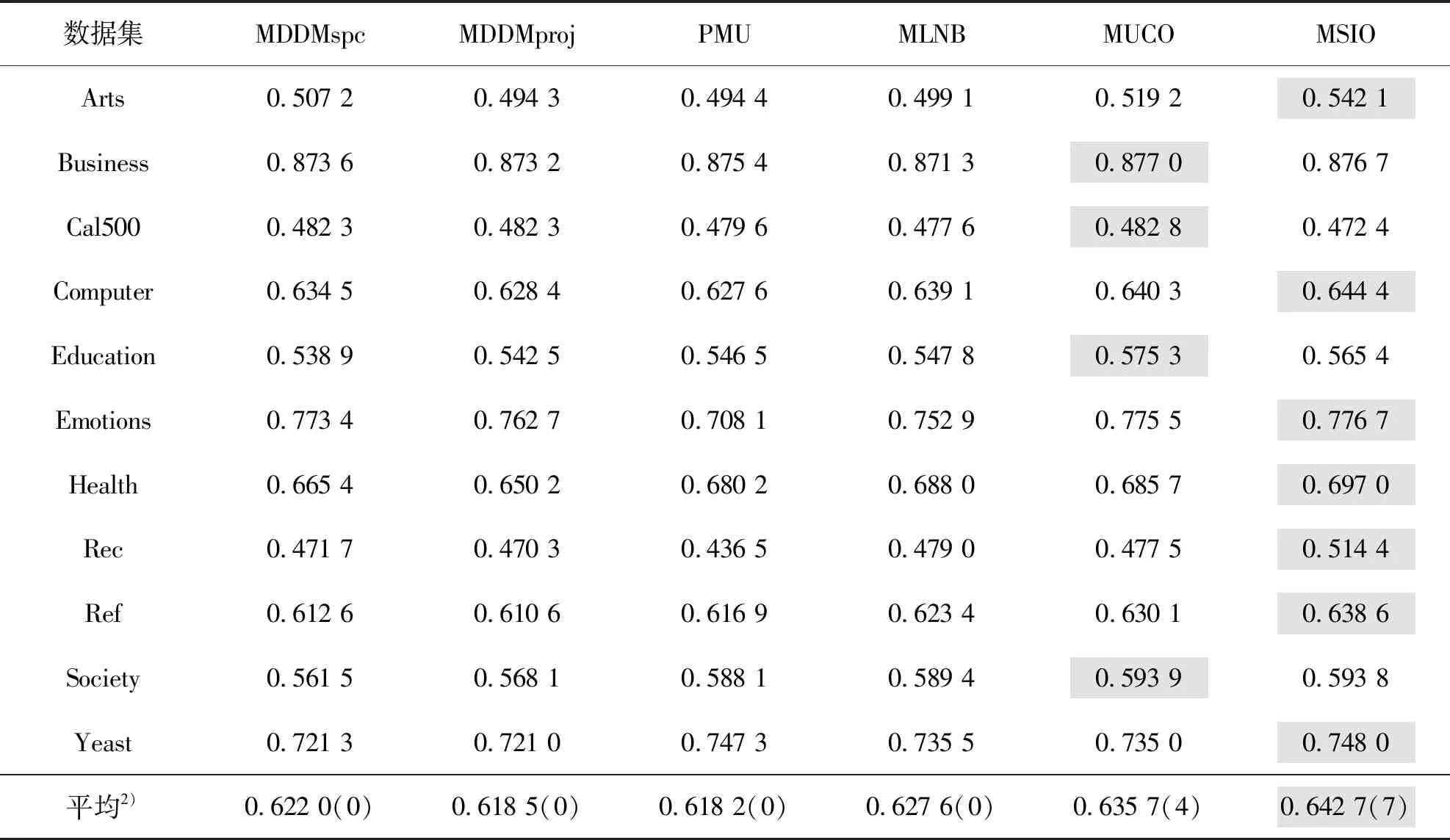
表2 六种算法在11个数据集中的平均准确率排序1)Table 2 Average precision ranking of 6 algorithms in 11 datasets

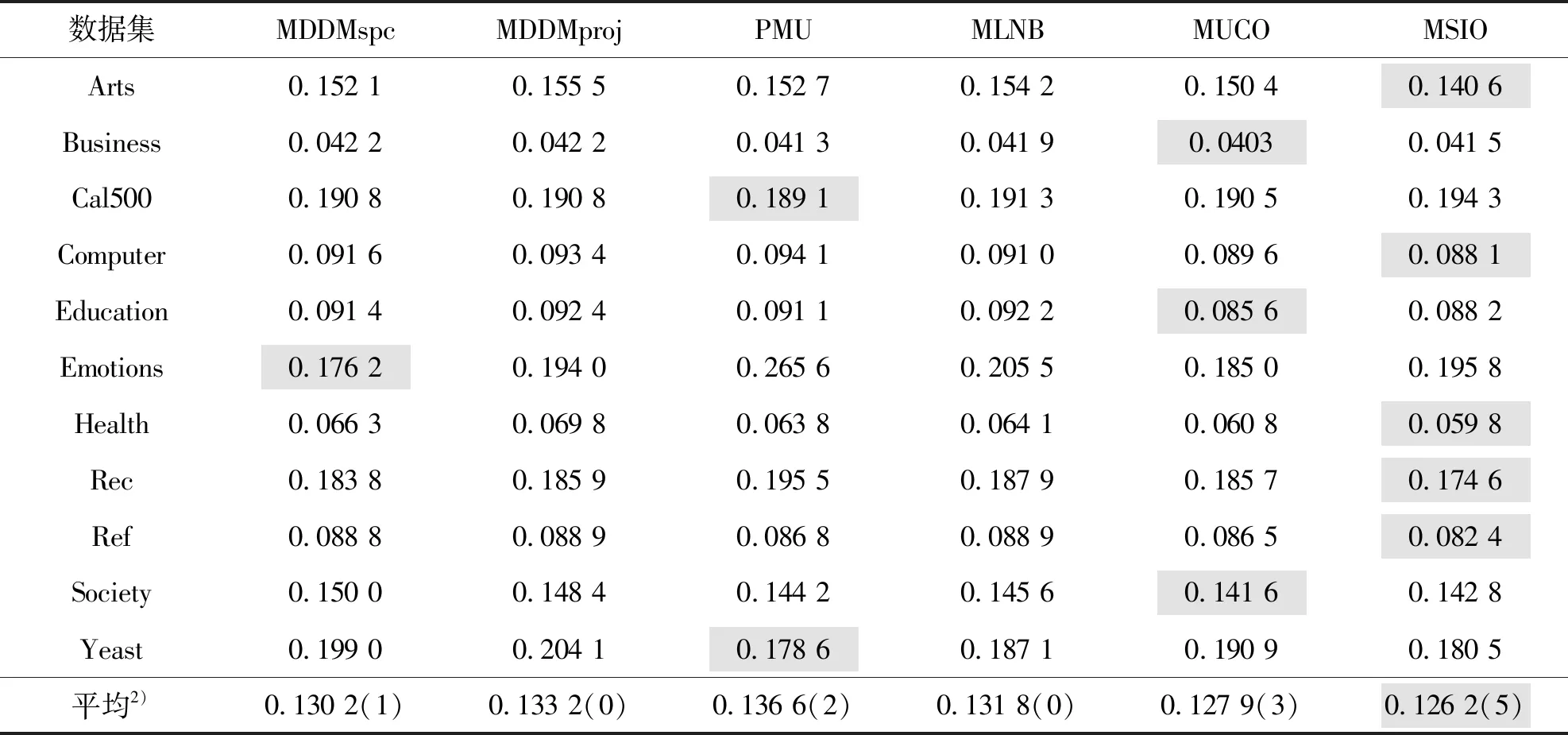
1)平均准确率指标越大越好，灰底数值表示在该指标上取得的最优结果； 2)括号内数字表示在11个数据集中算法获得最优值的个数 表3 六种算法在11个数据集中的排位损失排序1)Table 3 Ranking loss of 6 algorithms in 11 datasets

1)排位损失指标越小越好，灰底数值表示在该指标上取得的最优结果；2)括号内的数字表示在11个数据集中算法获得最优值的个数

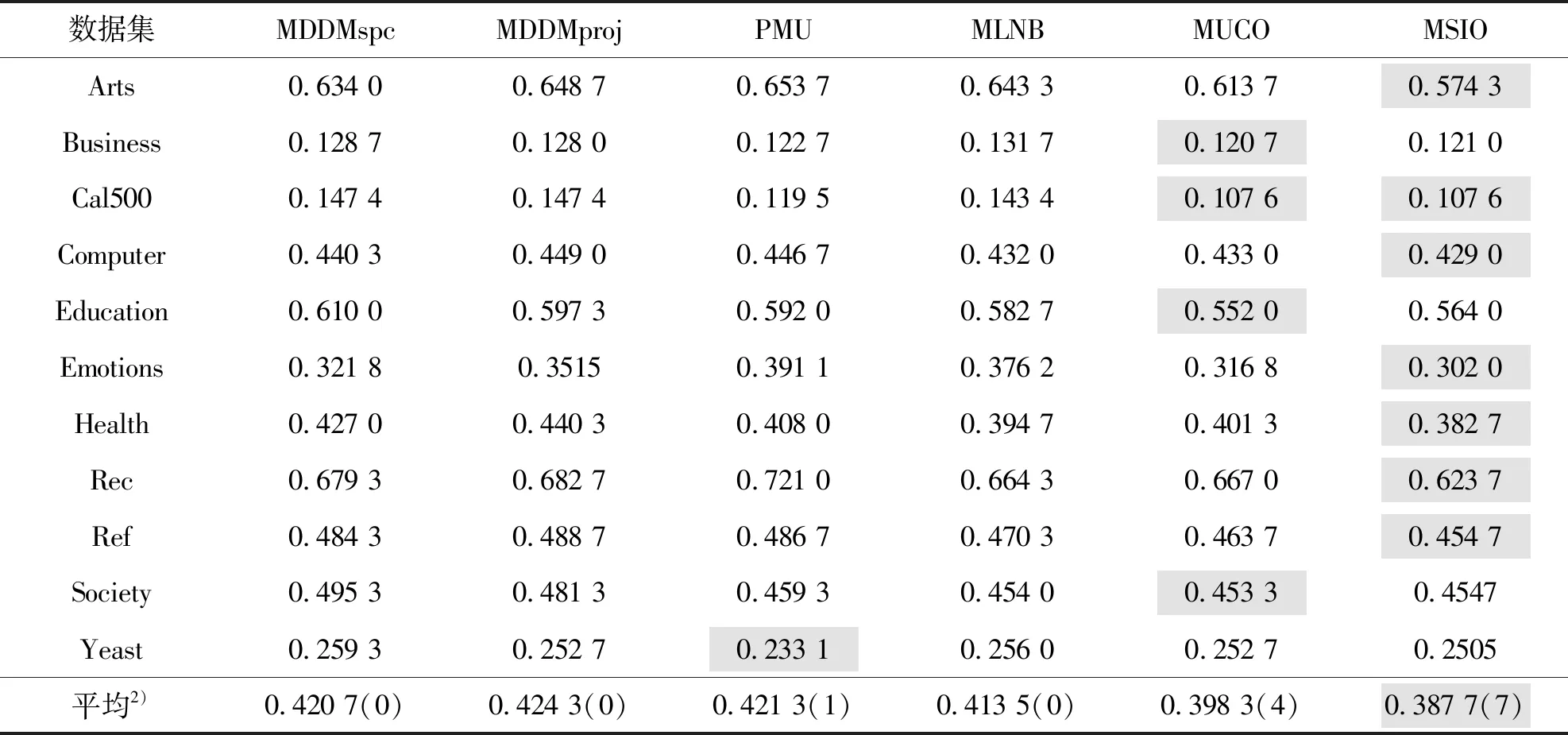
表4 六种算法在11个数据集中的1-错误上排序1)Table 4 One-error ranking of 6 algorithms in 11 datasets

1)1-错误指标越小越好，灰底数值表示在该指标上取得的最优结果；2)括号内数字表示在11个数据集中算法获得最优值的个数

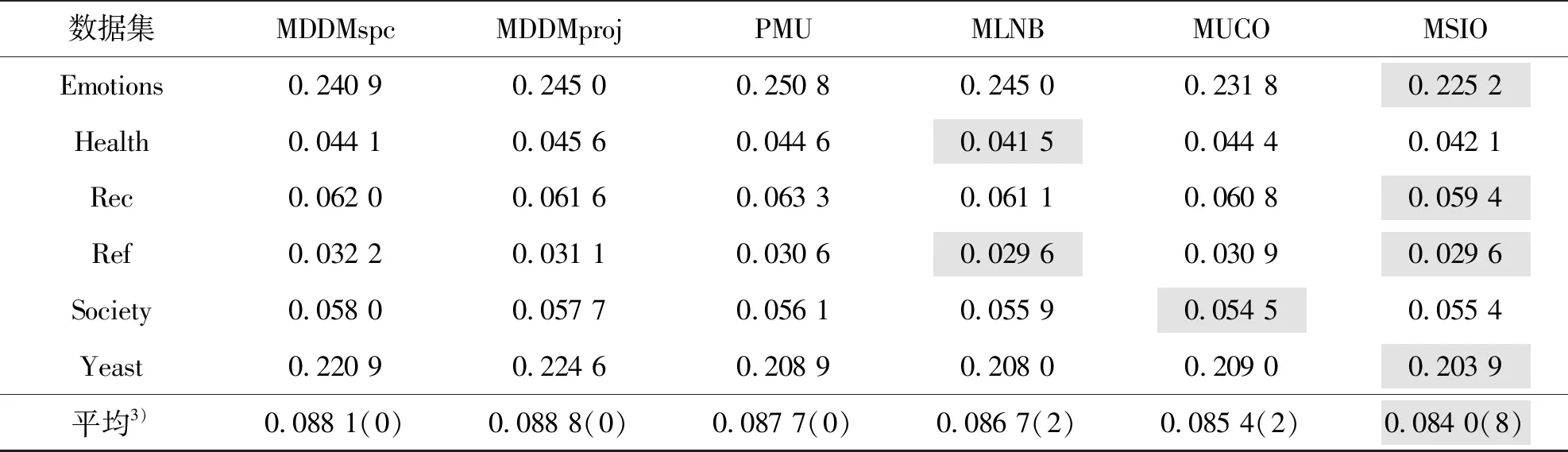
(续表5)

1)海明损失指标越小越好，灰底数值表示在该指标上取得的最优结果；2)括号内数字表示在11个数据集中算法获得最优值的个数

由表2至表5可见：

1)MSIO算法在4种评价指标中的最优数目和平均值均位列第1，且在Art、Computer、Rec和Ref数据集中的所有评价指标均优于其他算法．

2)在AP指标上，仅MUCO算法在部分数据集上占优，但最优的Cal500数据集也仅提高了2.15%；在RL指标上，6种算法各有千秋，其中，在Emotions数据集中MDDMspc算法占优最大，为11.12%；在OE和HL指标上，最优的分别高7.46%和3.58%．

图3为6种算法在不同评价指标上的箱型图．由图3可见，6种算法在4种评价指标上展现的分类性能对比中，MSIO算法在箱形图中的中位数表现明显占优．可见，MSIO算法稳定性更好的，且分类精度更高，性能优于其他特征选择算法．

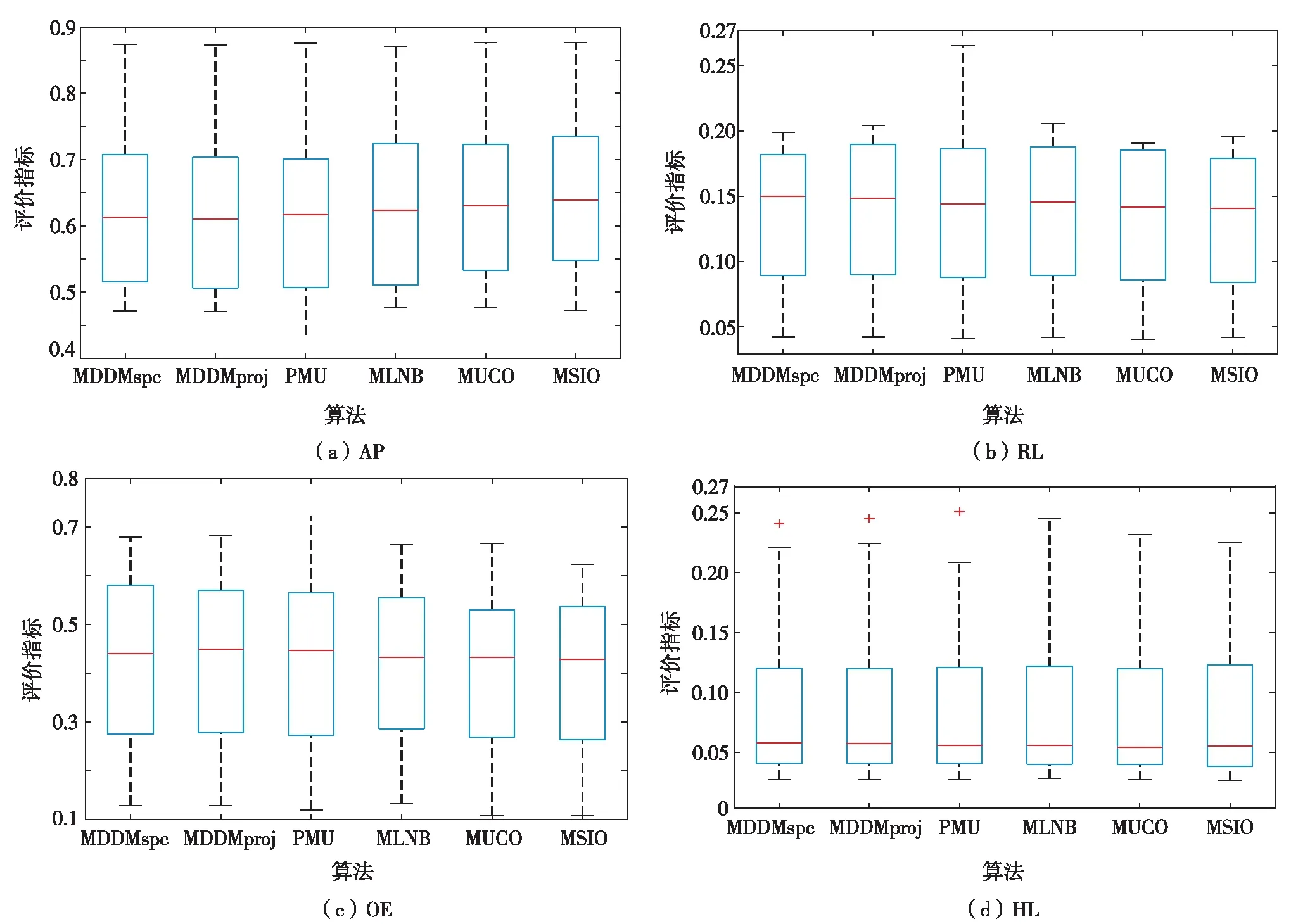
图3 六种算法在不同评价指标上的箱型图Fig.3 Box-plot of six algorithms on different evaluation indexes

3.4 算法性能统计分析

运用统计学知识，对在11个数据集上的实验结果进行显著性水平为5%的Nemenyi统计假设检验，若在所有数据集上两个对比算法平均排序的差低于临界差(critical difference, CD)，则认为它们无显著性差异，否则，认为这两个对比算法有显著性差异．本研究设显著性水平α=0.05，qα=2.850(第k个对应数)， 算法个数k=6， 数据集个数N=11，则

(16)

图4给出了各个算法在不同评价指标下的对比．坐标轴上的刻度描述了各种算法在不同指标中的平均排序，轴上数字越小，表明算法性能越优．不同线型相接的算法表示在性能之间无显著性差异．由图4可见，MSIO算法排名除在RL指标上比MUCO稍微逊色，在其余指标中均明显较优．

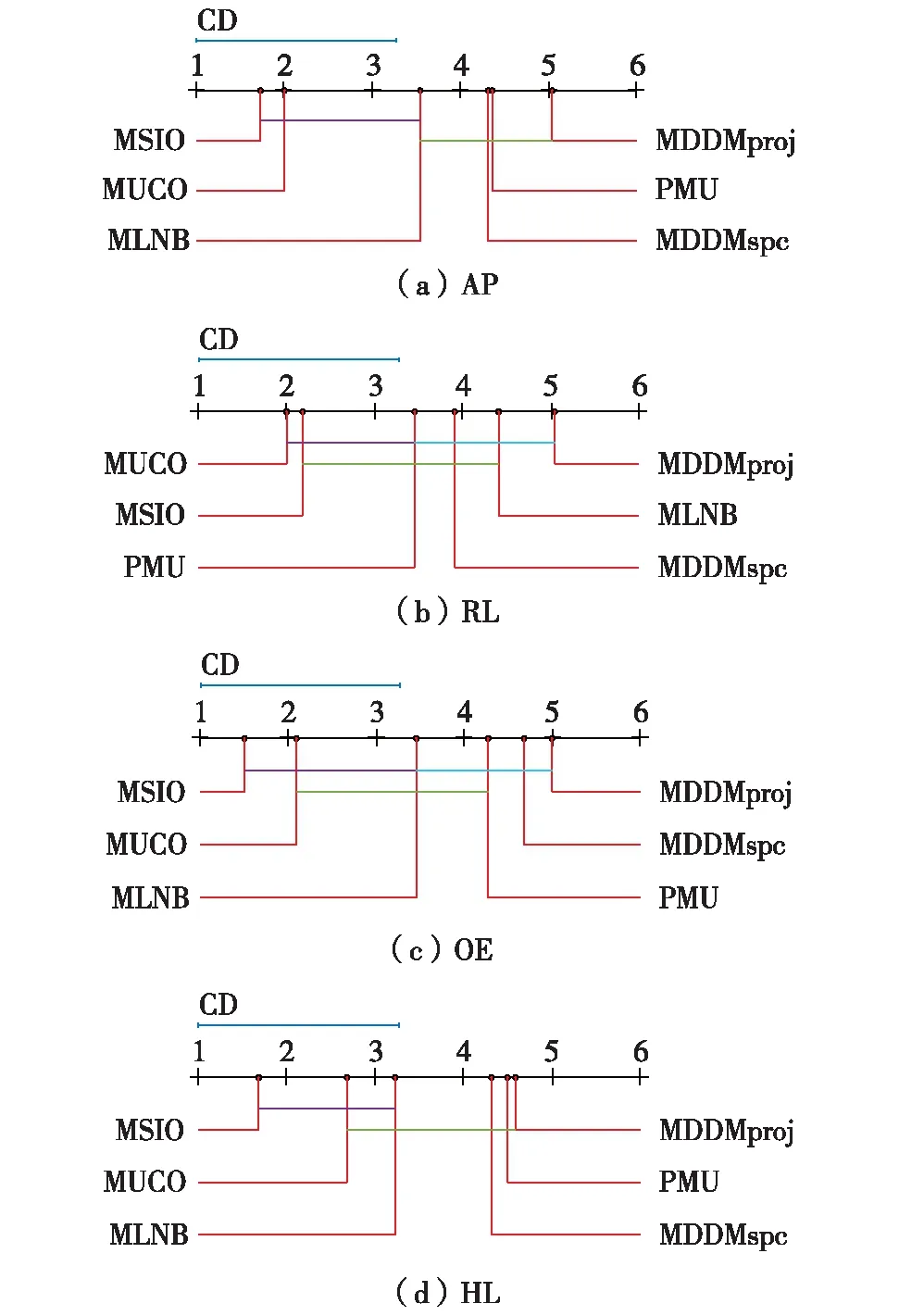
图4 各算法Nemenyi检验的性能对比Fig.4 Performance comparison of Nemenyi test of each algorithm

结 语

通过对不同标记在样本空间的描述程度存在一定的差异性的思考，结合信息熵的相关知识，提出一种不平衡标记差异性特征选择算法MSIO，通过不同标记下的正负标记权值修正传统的信息熵，由于加入了标记空间的信息，使选出的特征具有更加丰富的信息．在多组数据集上的多个评价指标中，MSIO算法性能都优于目前多数的特征选择算法．但是，MSIO算法在进行特征选择时仅考虑了特征与标记的相关性，而未对特征空间本身进行冗余性约简，这也是下一步的研究方向．