基于流固耦合的埋地供水管道地震响应分析

王丽娟，张家铭，张海潇，张 锐

河北工业大学土木与交通学院，天津 300401

埋地供水管道是城市的生命线，一旦在地震中遭到破坏，将会对城市的生产生活产生巨大的影响，并给城市的灾后重建带来不便，造成难以估量的人员伤亡和财产损失．现阶段中国埋地供水管道的抗震设计存在不足，抗震规范中管道受力模型主要参考拟静力分析法和反应位移法[1-4]，这些方法只能近似模拟地震作用下管土之间的相互作用力，而忽略了输流管道，特别是压力流管道与管内流体之间的流固耦合动力作用．管道在地震波作用下会发生振动，管道的振动会影响到管内流体的运动，流体流场的变化反过来又会影响到管道的动力学特性，使得管道与管内流体之间产生流固耦合效应[5]．考虑流固耦合时，管道的受力更接近于工程实际状况，计算结果也更精确[6]．因此，将流固耦合的理论应用于埋地供水管道抗震分析中具有一定的理论基础和现实意义．

国内外学者针对输流管道流固耦合受力计算进行了研究．FARHAT等[7]概述了流固相互作用问题的三场公式，其中流体由Euler方程或N-S方程建模，结构由有限元模型表示，流体网格是不稳定的．张挺等[8]应用有限积分法分别配合隐式欧拉法和拉普拉斯数值反演法，研究瞬时关阀时输流直管轴向耦合振动响应特性．陈坚红等[9]采用 C++ 语言编制了充流管道单向流固耦合数值模拟程序，模拟了管内流体压力分布以及将流体压力数据导入管道结构中进行管道应力计算的过程．周知进等[10]利用有限元的方法对不同曲率管道的流固耦合特性进行分析，并研究了流固耦合作用对不同曲率管道位置等效应力的影响．梁军等[11]通过ADINA软件建立了流固耦合有限元模型，研究了流固耦合作用下管道的抗震性能及管内介质和流速等参数对管道破坏的影响．从以上研究可见，流固耦合动力学分析的理论研究已基本形成体系，然而并没有学者对埋地供水管道在地震作用下的流固耦合动力学问题进行深入的研究．鉴于此，本研究将流固耦合动力学运用到埋地供水管道的地震响应分析中，以球墨铸铁供水管道为研究对象，利用ANSYS Workbench有限元软件建立埋地供水管道的流固耦合模型，施加土压力荷载和地震动力作用，分析在管-水流固耦合作用下管道总变形和等效应力，并改变埋深、管径、壁厚、流体流速及管道工作压力等参数，探究管道等效应力的变化情况，以期为埋地压力流管道的抗震设计、施工方法及力学模型分析提供参考．

1 埋地供水管道流固耦合理论基础

1.1 流固耦合控制方程

当考虑管水之间的流固耦合作用时，流体区域和固体区域应各自满足其基本控制方程．对于流体区域，假设管内水为可轻微压缩的均匀流，考虑其黏度，不考虑热交换过程，则其应满足流体质量守恒平衡方程和动量守恒平衡方程[12]．

质量守恒所对应的平衡方程为连续性方程，

(1)

其中，ux、uy和uz分别为流体在x、y和z三个方向上的速度分量；t为时间；ρ为密度．

动量守恒是在牛顿第二定律的基础上推导的，动量方程在x轴方向上的表达式[13]为

(2)

其中，V为流速矢量；P为流体压力；fx为单位质量力在x轴方向上的分量；σxx为流体在x轴方向上的正应力；τyx和τzx分别为沿y和z方向的切应力．

根据式(2)，同理可得到动量方程在y和z方向的表达式，此处不再详述．

对于固体区域，若管内水引发管道振动或位移，其控制方程[13]为

(3)

其中，Ms为固体质量矩阵；Cs为固体阻尼矩阵；Ks为固体刚度矩阵；r为固体位移；τs为固体所受应力．

将流体与固体进行耦合计算，首先要满足流体区域和固体区域在耦合边界上的运动学平衡方程和动力学平衡方程[14]．对于埋地供水管道，耦合面即为管道的内壁面，其运动学和动力学条件为

(4)

其中，df为流体的边界位移；ds为固体的边界位移；τf为流体应力；τs为固体应力．

对于无滑移壁面，流体流速v=ds； 当耦合界面发生相对滑移时，则有

nv=nds

(5)

其中，n为液体流动方向．

1.2 流固耦合有限元求解方法

利用有限元方法求解流固耦合问题，需要分别列出两者的有限元运动方程并联立．在引入有限元近似形函数和考虑耦合界面阻尼能量损耗的情况下，基于流体的连续性方程和动量方程，得到流体的运动方程[15]为

(6)

其中，Pe为流体压力；Ue为结构位移；Mef为流体的质量矩阵；Kef为流体的刚度矩阵；Cef为流体的阻尼矩阵；ρRe为耦合质量矩阵．

当固体结构受到流体施加的动水压力后，振动方程为

(7)

其中，Fe为外部荷载矩阵；Re·Pe为流体压力荷载矩阵．

通过联立式(6)与式(7)，得到流固耦合的有限元方程为

(8)

式(8)表明，在流固耦合面上，各个节点具有同样的位移和压力自由度，当流体区域和固体区域耦合面上的接触节点的解确定后，通过求解式(8)可确定耦合面上的解向量，从而解决流固耦合动力学问题．

2 管道流固耦合的有限元分析

2.1 建立管-水流固耦合模型

运用1.1节中的流固耦合理论基础建立管-水流固耦合模型．该模型由流体相和固体相两部分组成，两相交界的耦合面包含管道内壁面和流体外壁面．建立模型时应首先应根据管道的几何尺寸建立管道固体区域模型，之后填充管道，填充生成流体区域，从而将流固耦合面划分为两个面．本研究根据文献[16]，选择研究对象为DN500(管道公径直径为500 mm)的直管道，长度为6 000 mm，管道外径为532 mm，壁厚取10 mm．

2.2 划分管道网格

管道的网格划分采用六面体8节点单元．管道网格划分的精细程度会对模型后处理计算结果产生影响，网格划分越精细，网格单元越密集，计算结果越精确，所需计算时间也会更长．本研究采用高光滑度和细化跨度中心角的网格，最小网格长835.66 mm，共划分45 796个节点，6 776个单元．

2.3 流体的动网格模型

当管道在地震波的作用下发生振动时，流体网格会在管道的带动下会产生收缩和膨胀．此外，当固体耦合面的数据传递到流体耦合面时，流体网格需要作出相应的调整，因此产生了流体的网格移动问题．在推导数学模型时，可以通过将Euler坐标下的N-S方程映射到任意拉格朗日-欧拉(arbitrary Lagrange-Euler， ALE)坐标系统中来解决动网格问题，即在流体区域中采用Euler单元，对固体区域内用Lagrange单元，并在统一的ALE坐标系下进行求解，使得流体模型中的流固界面总是跟随固体的变形而改变[17]．

在流固耦合分析中，流体的网格划分方式将直接影响计算结果的收敛性和精确性．如果依旧采用六面体8节点单元的划分方式则会增加网格的畸变率，在计算过程中很有可能产生负体积，导致计算结果不收敛，因此，本研究采用四面体单元对流体网格进行网格划分．在ANSYS Workbench中，通过采用弹性光顺法和局部网格重构法来对动网格问题进行求解，设置弹簧屈服强度系数为0.5，拉普拉斯节点松弛系数为0.5，网格重构中单元和面的最大偏度分别为0.4和0.6，网格尺寸重分布间隔为10，共划分3 808个节点16 902个单元．

2.4 设置材料参数

模型建立且网格划分完毕后，需要对模型的流体区域和固体区域分别赋予对应的材料属性．其中，流体材料为液态水，密度为998.2 kg/m3；固体材料为球墨铸铁，其参数如表1[16]．

表1 球墨铸铁管材料参数[16]Table 1 Material parameters of ductile cast iron pipeline

在ANSYS Workbench中需要在Engineering Data模块下设置与定义球墨铸铁材料，并输入材料参数，以便于在建立模型后将材料属性赋予给管道固体区域．

2.5 模型的边界条件

图1为埋地供水管道的受力示意图．其中，M为管道覆土厚度；D*为管顶至管道开挖沟槽底面的距离．本研究模型中，设置管道的两个端面为固定约束，数值模拟计算范围等同于管道的计算长度．

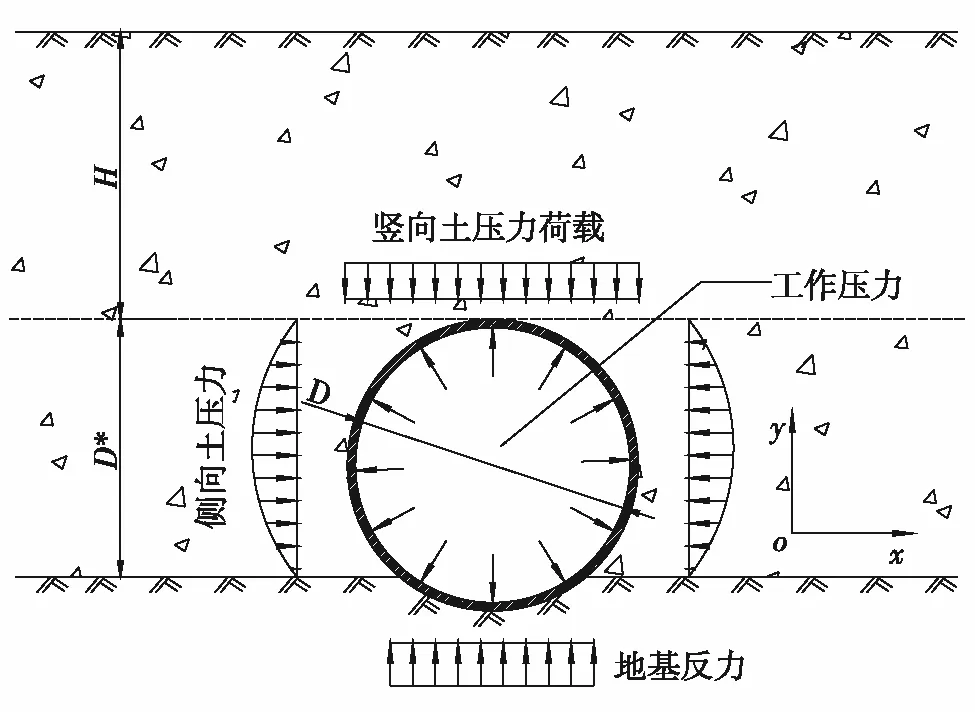
图1 埋地供水管道受力示意图Fig.1 Stress diagram of buried water supply pipeline

取管道埋深为2 m，并考虑管道与管内水自重的影响．在静载作用下，管道左右两侧的土压力相互平衡，地基反力的大小与竖向土压力荷载、管道与管内流体自重及地基承载力的大小有关．

为简化计算，本研究将作用在管道上的土压力荷载等效为均布荷载，并忽略侧向土压力和地基反力，即只考虑竖向土压力荷载对管道的影响．竖向土压力荷载作用在管道外表面的上半部分，计算式[18]为

Fsv,k=CdγsHsBc

(9)

其中，Fsv,k为等效竖向土压力荷载；Cd为土压力系数；γs为回填土重力密度；Hs为管顶至地面的覆土高度；Bc为管道的外径．

对于管内流体部分，设置管内流体为标准k-ε的湍流模型，忽略流体在运动过程中与管壁产生的热量交换，并分别定义流速入口端面和流速出口端面，与管道端面平齐，且为自由平面，不设置约束．在出入口端面上，流体速度为绝对速度，大小为1.2 m/s，方向为垂直于边界，并取湍流强度为5%，湍流黏度比为10．

当供水管道处于工作状态时，管内为压力流，取工作压力为0.6 MPa．对于流固耦合面，设置流体在流经管道壁面时不与管道壁面产生滑移，并取耦合面的粗糙度常数为0.5．

2.6 施加地震动力作用

本研究选取国内外结构抗震设计常用的美国Northridge地震中观测到的地震波数据，并取前10 s计算时间，作为埋地供水管道模型的地震动力荷载[19]，加速度时程曲线如图2．

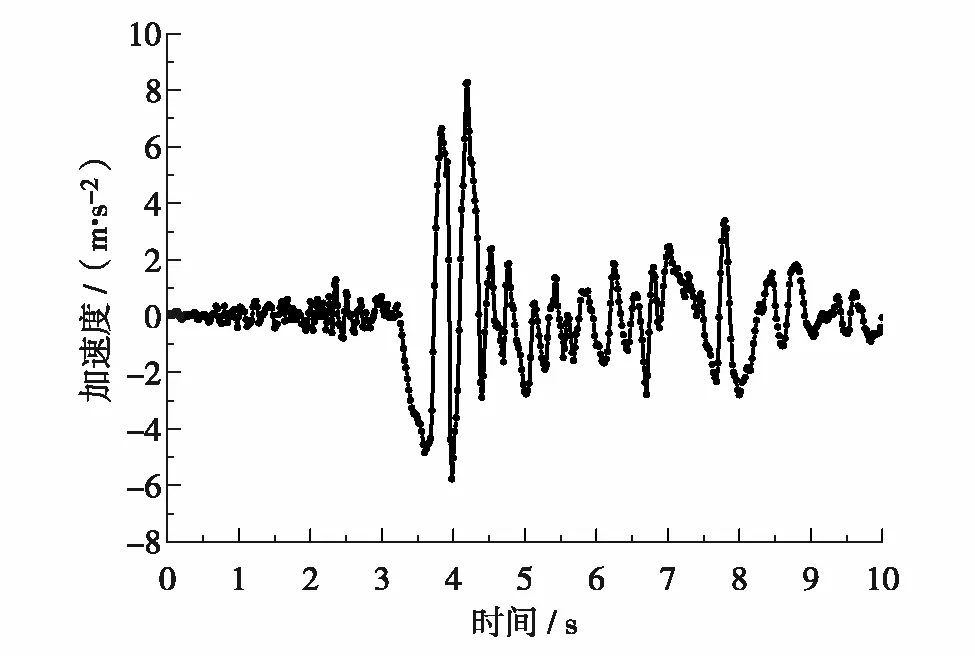
图2 地震波的加速度-时间曲线Fig.2 Acceleration-time curve of seismic wave

该地震的震级为里氏6.7级，地震波峰值加速度的平均值在0.3g以上，前10 s的最大地震加速度约为0.8g， 按照中国抗震设计规范的标准，对该地震波作用下的构筑物进行抗震设计时，需要按照抗震设防烈度为8度来考虑[20]．

在ANSYS Workbench中，需要利用Transient Structural模块将地震动力作用施加在管道上．设置总作用时间为10 s，以0.02 s为1个时间步长，输入每个时间点所对应的地震波加速度，共输入500组数据，对应加速度时程曲线上的每个点，便可以模拟供水管道在地震波作用下的振动情况．地震波的传播方向设置为沿着管轴方向和垂直于管轴方向，同时进行传播．

2.7 流固耦合模型求解

管道和管内流体之间的耦合是一种双向流固耦合，计算原理可参考式(8). 采用牛顿-拉夫森迭代法，在每个时间步上将固体区域的计算结果加载至流体，引起流体流场变化后重新计算流体，将新的结果重新作用在固体区域上，以此反复迭代，得到最终的收敛结果．在ANSYS Workbench中，需要将设置好的流体区域和固体区域通过System Coupling模块进行迭代计算，并设置计算时间步长、流体与固体的迭代顺序以及总计算时长，从而实现模型的求解．迭代求解法计算量大、耗时较长，对计算机的性能要求较高，在模拟过程中需要考虑迭代收敛性和计算效率问题．

3 流固耦合模拟结果分析

当地震波加载至4.2 s时，管道的总变形达最大值，云图如图3．由图3可见，最大值出现的位置在管道中部，这是因为管道两端固接，管道中部的位移约束小，在地震波作用下振幅较大，所以相较于管道其他位置，管道中部的总变形最大．

图3 t=4.2 s时管道的总变形云图Fig.3 (Color online) Total deformation nephogram of pipeline at 4.2 s

图4为埋地供水管道模型在地震作用下管段中部的总变形随时间的变化曲线．从总体上看，管道中部下端的变形比上端的变形高3.8%，在地震刚开始的一段时间内，由于地震波的加速度数值较小，变化幅度不大，所以管道产生的振动也不明显，管道产生的变形主要来自于管和水的自重以及管顶的竖向土压力荷载．随着地震的持续进行，地震加速度逐渐达到峰值，管道的变形受地震作用的影响较为显著，且变化趋势与地震波的加速度时程曲线变化基本一致．

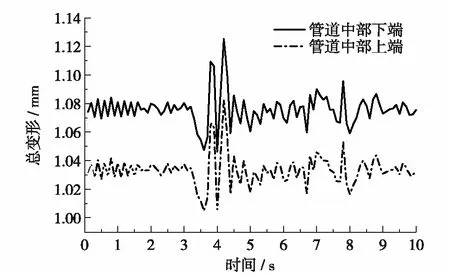
图4 管道中部总变形时程曲线Fig.4 (Color online) Time history curve of total deformation in the middle of the pipeline

同样当地震波加载至4.2 s时，管道的等效应力也达到最大值，云图如图5．最大等效应力的位置在管道的出口，这是由于模型假定管道两个端面不发生变形和移动，当管道中部产生变形后，距离中部越远的管段所产生的应力就会越大，并且地震波作用方向为管道出口，因此管道出口的等效应力要比管道入口更大．

图5 t=4.2 s时管道的等效应力云图Fig.5 (Color online) Equivalent stress nephogram of pipeline at 4.2 s

在模型的计算过程中，由于管道一直处在振动状态，管-水耦合界面也相应发生扩张和收缩．流体的动网格算法根据流体边界的变化不断地更新网格，通过拉伸或重新生成网格来适应流体区域的变化，确保管-水耦合界面处于高度耦合状态，并且能够有效地在两相之间传递计算数据．

4 影响管道等效应力变化的因素

4.1 管内流体流速的影响

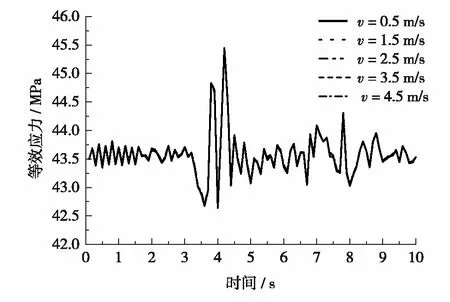
图6 不同流速下管道的等效应力Fig.6 (Color online) Equivalent stress of pipeline under different flow velocities

其他条件不变，改变管道内流体的流速分别为0.5、1.5、2.5、3.5和4.5 m/s，探究流速变化对地震作用下埋地管道等效应力变化的影响，结果如图6．从图6可以看出，管道的等效应力并没有因为流速的改变而发生明显的变化，这是因为管道内流体的密度和体积不随流速的改变而改变，在忽略流体惯性力的条件下，流体质量不变，对管道产生的作用力也不变，所以管道等效应力也不变，这与文献[11]中的结论相符．因此，可以认定在合理的流速范围内，管道内流体流速变化并不影响地震作用下管道的等效应力大小．

4.2 管道工作压力的影响

其他条件不变，分别选取管道工作压力为0.4、0.6、0.8、1.0和1.2 MPa，对比管道在不同工作压力下的等效应力，结果如图7．由图7可见，随着工作压力的增大，管道的等效应力也随之增加．这是因为工作压力增大时，管道内壁会受到动水压力的作用发生变形，管道环向应力增大，致使管道等效应力增大．但是，管道工作压力从0.4 MPa至1.2 MPa增长了3倍，等效应力只增加了31.4%．对于采用柔性连接的DN500球墨铸铁管，允许工作压力约为4.4 MPa，因此在安全工作压力下，管道工作压力增大会使管道在地震作用下的等效应力增大，但等效应力增长比率远小于工作压力增长的幅度．

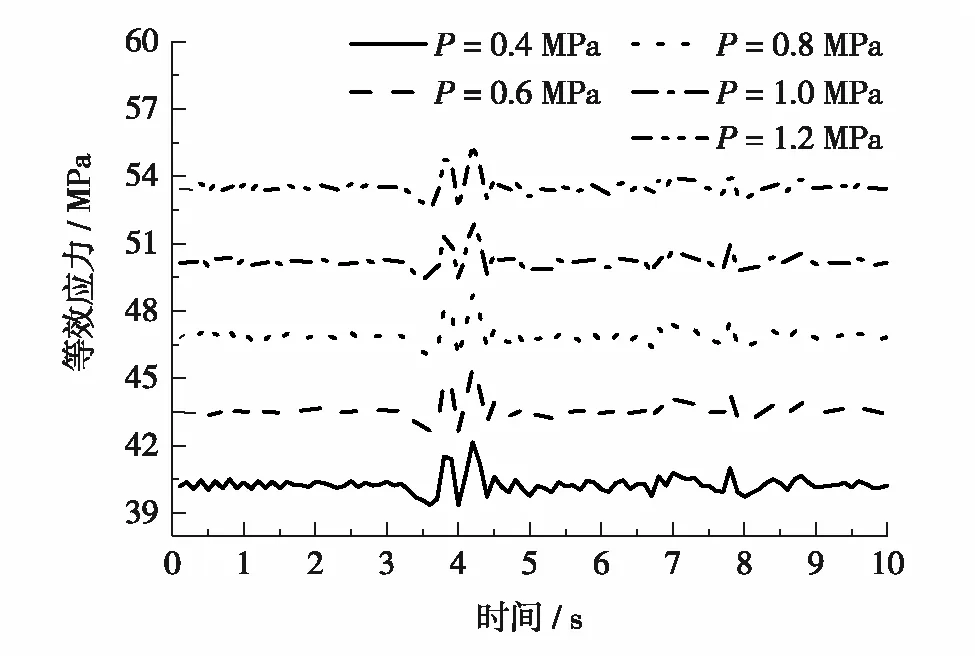
图7 不同工作压力下管道的等效应力Fig.7 (Color online) Equivalent stress of pipeline under different working pressure

4.3 管道埋深与管径的影响

图8 不同埋深和不同公称直径下管道的最大等效应力Fig.8 (Color online) Maximum equivalent stress of pipeline with different buried depth and different nominal diameter

图8给出了在壁厚均为10 mm，埋深分别为2、3、4、5和6 m时，DN300、DN500、DN800、DN1000和DN1200五种不同规格管道在地震波加载过程中最大等效应力的变化情况．从图8可见，不论对于何种公称直径的管道，最大等效应力均随管道埋深的增加而增大．这是因为在地震发生后，地表裂缝呈楔形，土体位移随埋深增大而减小[21]，在不考虑地面面波和场地大变形的前提下，当埋深增大时，作用在管道上方的竖向土压力荷载增大，在地震的作用下土压力的增大会对管道振动的约束作用增大，导致管道等效应力增大．

此外，随着管道公称直径的增大，管道在地震中所受到的最大等效应力先减小后增大，其中，DN800的管道在其他条件相同的情况下等效应力最小．这说明了管径的增大有利于提高管道的抗震性能，但是随着管径的增大，管道和管水的重力也增大，自重对等效应力的影响逐渐占据主导地位，在地震过程中振动惯性力加大，故当管道公称直径超过800 mm时，管道等效应力反而增大．

4.4 管道壁厚的影响

按照球墨铸铁管的规格标准，不同公称直径的管道所采用的管道壁厚不同．甚至在相同公称直径的管道下，管道壁厚也有着不同的取值．表2给出了不同公称直径球墨铸铁管在工程上常用的壁厚取值[16]．其中，K8、K9和K10为球墨铸铁管的壁厚等级．

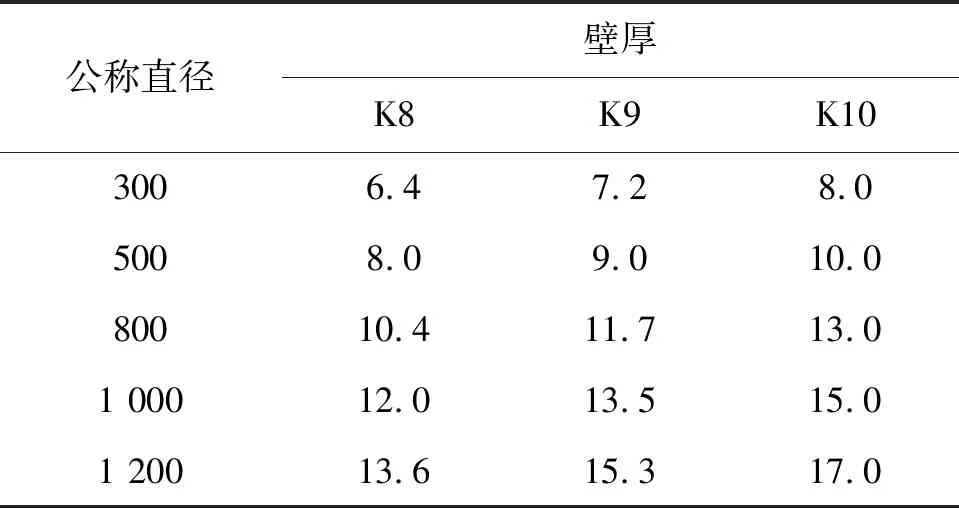
表2 不同公称直径下管道的壁厚[16]Table 2 Wall thickness of pipeline with different nominal diameters[16] mm

为更直观地反映管道壁厚对管道等效应力的影响，保持其他条件不变，在不同公称直径下管道分别取标准壁厚和统一壁厚，标准壁厚取表2中的K8列数据，统一壁厚取10 mm，并将计算结果作对比．

图9显示了不同管径下管道的等效应力. 由图9可见，在同一公称直径的管道中，等效应力越小，所对应管道壁越厚，且壁厚差距越大，等效应力差越大．这是因为管壁越厚，管道的刚性越大，管道在地震波影响下的振动强度越小，管内流体对管壁的冲击力减弱，管道的流固耦合作用力降低，管道等效应力减小，所以厚壁埋地供水管道的抗震性能比薄壁埋地供水管道更好. 当取统一壁厚时，可明显看出DN800的管道等效应力最小，印证了4.3节的结论．因此，在满足规范设计要求以及经济合理的范围内，在管道的抗震设计中应尽量采用管道公称直径在800 mm左右且管壁较厚的管道．

图9 不同管径下管道的等效应力Fig.9 (Color online) Equivalent stress of pipeline with different diameters

5 结 论

基于流固耦合理论，建立了地震作用下埋地供水管道管-水流固耦合模型，实现了管道在地震动力作用下的流固耦合计算及抗震模拟. 改变管内水的流速、管道工作压力、管道埋深、管径以及壁厚，对比了不同参数影响下管道最大等效应力的变化情况，可知：

1)采用流固耦合模型进行管道地震响应分析，与传统分析方法相比省略了很多假设性条件，具有模型简易，计算过程简便等优势，得到的结果与现有研究相符，佐证了本研究模型在管道抗震方面的可行性和正确性，是流固耦合仿真研究的一种新运用途径，可为现阶段埋地供水管道抗震设计规范的补充，也可以推广至输油、输气等压力流管道的抗震计算中．

2)埋地供水管道在地震波的作用下会发生受迫振动，当地震波的加速度达到峰值时，管道的变形和等效应力也达到了峰值，最大变形出现在管道模型的中部，最大等效应力出现在管道的出口端．

3)在地震波作用下，管道内流体的流速对管道等效应力几乎没有影响，管道工作压力的增大会使得管道等效应力增大，但影响不明显. 所以在一般情况下，可以认为管内流体流速对管道抗震性能没有影响，工作压力变化对管道的抗震性能有较小的影响．

4)管道深埋以及增大管道壁厚，都可以减小管道受震下的等效应力．除此之外，管径变化对管道等效应力有较大影响. 在管径较小时，管道的等效应力很大，随着管径的增大，管道的等效应力减小.采用DN800管道时管道等效应力最小，管径继续增大，管道等效应力随之增大，因此在管道设计上需要考虑最佳的管径取值．