轨道清污车吸污效率影响参数正交试验研究
张 灵 史天亮
(1.湖南工业大学机械工程学院 湖南 株洲 412007;2.中国铁建重工集团有限公司 湖南 长沙 410100)
随着我国铁路交通运输的发展,一系列用于高效清除铁路道床表面污物、障碍物的“铁路清道夫”产品应运而生:普遍用于清除高铁线路道床污物的吸污车,适用于沙漠线路的除沙车和运煤专线的吸煤车,通过这些专用车辆对铁路线路的维护,保证列车高速运行的安全性。
吸污效率的高低是衡量该类轨道清污车辆性能好坏的关键,为提高吸污效率,在样车研制阶段,研发工作者做了大量的理论计算、试验研究和样机改进工作,其目的是确定主要工作装置结构的合理性和运行参数的最优性。郭关柱在忽略空气的黏性力和密度变化、吹风口偏角与气流离开轨道表面角度的差异以及吸风对吹风影响的前提下,对新型轨道吸污装置的吸污能力进行了研究,分析了车辆临界移动速度、吹风口偏角对吸污能力的影响规律[1],后又对能耗和吸污能力进行分析[2];史天亮利用 Fluent 软件对铁路道床吸污车吸尘装置内部流场进行数值模拟,在不同参数情况下对吸尘效率进行仿真研究[3]。然而,由于影响吸污效率的因素较多,因素间存在着相互作用,导致实际值与仿真或理论计算有较大差距,甚至无法满足作业要求,出现吸污车样车实际吸污能力不足的现象,针对该车工作装置结构和设计参数等方面的问题,进行了大量的优化改进和试验验证研究。为此,在吸煤车研制过程中,为减少反复试验和样机调试次数,结合上述研究结论,选取三个对吸污效率影响最大的运行参数设计正交试验,对各影响因素的显著性进行分析,确定吸煤车工作装置关键结构及运行参数的优选组合方案,并建立了较为准确的煤粉除净率评价指标回归模型。
1 问题分析
1.1 吸污工作方式
吸煤车采用吹吸结合的吸污工作方式,如图1所示,吸风口前后布置吹风口,风机开启后,道床表面的煤粉被吹风气流及滚刷卷起后,由吸风气流吸入到除尘设备中。吸煤车主要清理对象为煤粉颗粒,煤粉颗粒的临界启动速度由颗粒当量直径决定[3]。由尘粒启动理论可知:当近地面气流速度大于启动速度时,尘粒才能被顺利吹起[4]。在煤粉颗粒从启动瞬间到进入吸风口的过程中,同时受到吹风气流、吸风气流和车辆走行速度的相互作用影响,处于复杂湍流环境中,在理论计算和建模仿真时容易被忽略或简化。
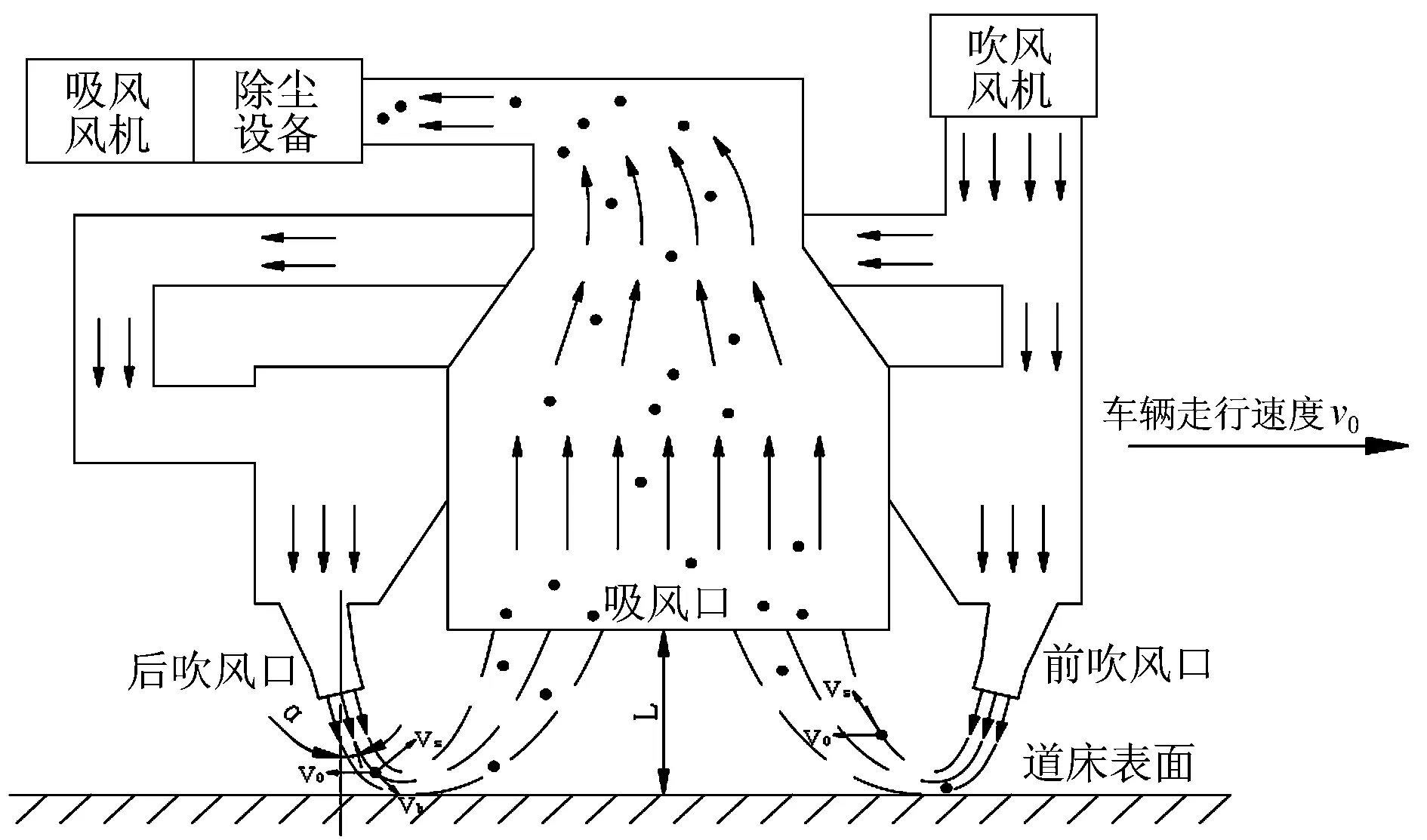
图1 清污工作方式示意图
1.2 正交试验设计
正交试验法具有“均匀分散、齐整可比”的特点[5],相比于普通试验的优势在于最大限度地减少了试验次数,且在较少试验次数的基础上,利用试验数据分析得出正确结论。运用既有的研究成果,通过对吸污效率的影响关系、影响趋势及其权重进行预判,选取以下3个影响因素:(1)吸风口与道床距离L;(2)吹风口偏角α,即吹风口与钢轨垂直面的夹角(见图1);(3)车辆走行速度v0。将吹风口位置、气流扩散以及测量精度等因素视为通常水平,设定额定吹风风量为30 000 m3/h、额定吸风风量为70 000 m3/h。
试验以单位面积内煤粉的除净率P(表面残留污物与试验放置量比值)、可吸收煤粉的最大粒径D作为评价该车吸污效率的主要指标。选用L9的正交方法安排试验(L为正交表的代号,做9次试验),根据上述三个影响因素,每个因素取3个水平值,试验各因素及水平如表1所示。
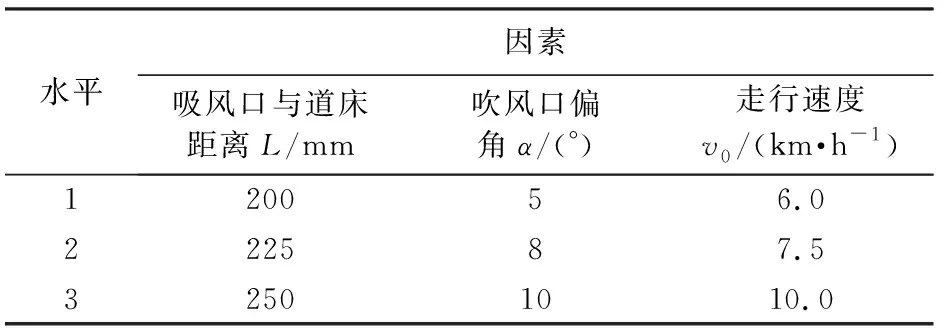
表1 正交试验因素和水平
选取厂内一段有砟轨道线路,沿道床表面均匀铺设厚度为10 cm、当量直径为1~25 mm不等的煤粉颗粒,清污作业前如图2(a)所示。

(a)清污作业前 (b)清污作业后(试验编号9)图2 吸煤车作业试验情况
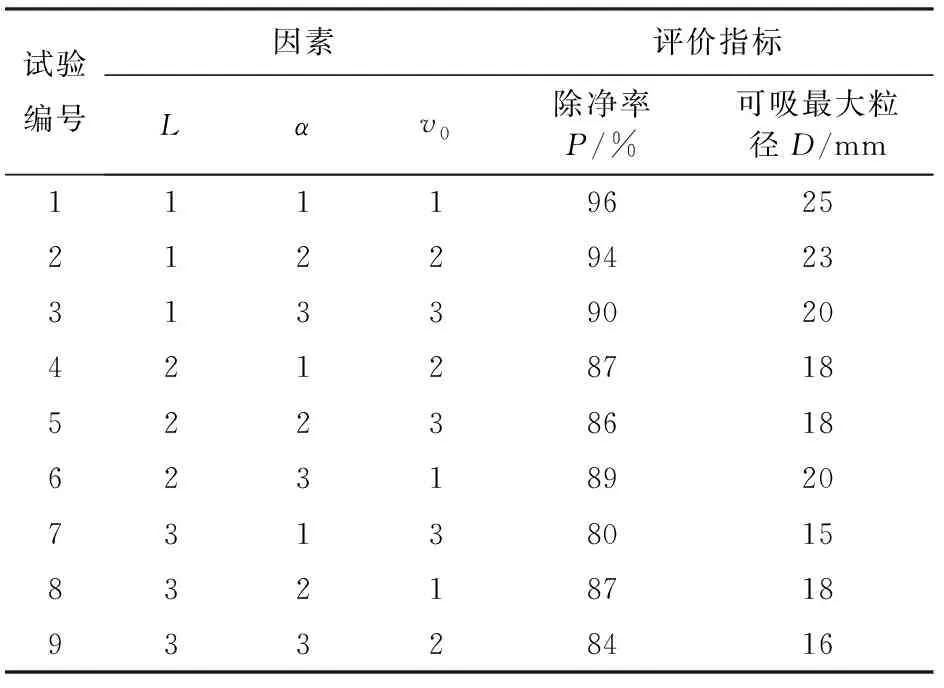
表2 正交试验结果数据记录
2 试验结果分析与参数优选
极差分析法简单易懂,实用性强,通过极差分析法分别计算吸风口与道床距离L、吹风口偏角α、走行速度v0对试验评价指标的影响程度。对除净率和可吸煤粉的最大粒径这2个试验评价指标的极差计算结果和优选组合方案的选取,分别如表3、表4所示。表中,ki表示因素L、α、v0的第i(i=1, 2, 3)个水平所对应的评价指标值之和的平均值。R为任一列因素的极差,R=max{k1,k2,k3}-min{k1,k2,k3}。
极差值用于反映因素水平的变化对试验指标的影响程度。极差值越大,所对应的因素对试验指标的影响越大,因此,可以依据极差值判断因素的主次。从表3、表4的极差值大小顺序可看出,因素主次是相同的,即对除净率和可吸最大粒径影响最大的是吸风口与道床距离L,其次是走行速度v0,最不显著的是吹风口偏角α。
ki值用于判断因素水平的最优选组合方案。由于试验评价指标除净率和可吸最大粒径皆为越大越好,所以应取各列中ki的最大值所对应的水平作为提高除净率和可吸最大粒径的优选方案。
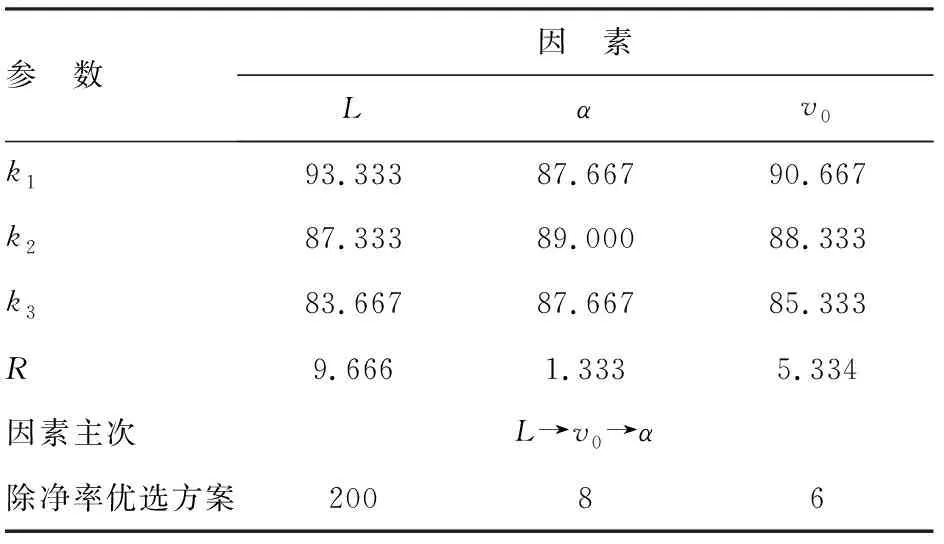
表3 除净率P极差分析结果

表4 可吸最大粒径D极差分析结果
根据表3、表4中同一列ki值的大小,确定参数优选组合方案为“L1、α2、v01”,该方案的参数设置值应优于上述正交试验的9种组合。在额定风量条件下,该方案既能保证吸煤车较高的吸污除净率,又能尽可能地清除较大颗粒的煤粉:(1)吸风口离道床表面距离越小,风速衰减越少,即到达道床表面的风速越大,越有利于将吹起的尘粒吸入,受钢轨高度限制,为保证一定安全距离,取吸风口距离道床表面的最小值L=200 mm;(2)随吹风口偏角增大,到达道床表面的吹风气流减小,但吹风口偏角过小,显然不利于污物颗粒随吸风气流进入吸风口,考虑到吸风气流的影响,根据试验极差分析结果选取吹风口偏角α=8°;(3)道床表面被吸面积远大于吸风口面积,走行速度v0越慢,有效作业时间越长,能够被吸起的污物粒径越大,越容易将污物颗粒吸走,但根据铁路线路作业“天窗点”时间的要求,走行速度不宜过低。
3 建模与回归
3.1 建立试验指标的回归模型
回归模型采用建模方便、拟合精度较好的幂函数形式,除净率P的回归模型为
(1)
其中,c、k、q、t为回归待定系数。
多元非线性必须转化为多元线性回归才能估计待定参数,对式(1)两边取自然对数得:
近年来,随着农村经济的发展,农业经营方式加速转变,农民合作社、龙头企业、专业大户、家庭农场等新型农村经营主体已成为农业和农村经营的主要力量。与传统的小农经济相比较,农村新型经营主体的经营理念、经营方式均发生了根本变化,农业经济的集约化、专业化、组织化、社会化水平显著提高,对农村金融产品和服务的需求呈现出新的特征。
lnP=lnc+klnL+qlnα+tlnv0
(2)
令lnP=y,lnc=b0,lnL=x1,lnα=x2,lnv0=x3,k=b1,q=b2,t=b3。模型转化为多元线性关系
y=b0+b1x1+b2x2+b3x3
(3)
该线性方程共包含3个自变量x1、x2、x3,由9组试验数据建立多元线性回归方程,将其表示成矩阵方程的形式
b=[b0b1b2b3]T
(4)
式中:Y为9组试验测量出的除净率对数值组成的矩阵,由最小二乘法可得
(5)
根据式(5)可得c=e7.3681,k=-0.492 4,q=0.008 5,t=-0.119 3,代入式(1)得到的除净率P的回归模型为
P=e7.3681L-0.4924α0.0085v0-0.1193
(6)
同理可得可吸最大粒径D的回归模型
D=e11.5677αp-1.4657vs-0.0108vw-0.3288
(7)
3.2 回归模型的误差验证
根据公式(6)、(7),分别对除净率P和可吸煤粉最大粒径D进行计算,验证回归模型的误差情况,产生最大误差时对应的试验编号和相应结果如表5所示。
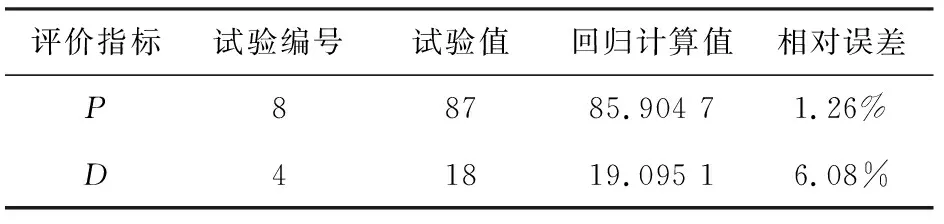
表5 最大误差时对应的回归计算值与试验值比较
由表5可知,根据回归模型得到计算值与相应试验的测量值之间的最大相对误差值分别为1.26%和6.08%,说明模型建立比较准确。可吸煤粉最大粒径误差值较大的原因主要是污物颗粒当量直径测量的不准确性,同时,复杂的吸污过程还受其他多种因素影响。
利用该回归模型,验证极差分析确定的优选实施方案为“L1、α2、v01”,可达到95.9%的除净率和25.3 mm的最大粒径值。
样车调试完毕后,吸风口与道床距离L和吹风口偏角α两个参数将保持固定不变,但轨道清污车辆作业走行速度v0可调。因此,可利用该回归模型,对除净率和可吸煤粉最大粒径值进行预测,并根据作业“天窗点”时间调整车辆走行速度。
4 结论
(1)通过对轨道清污车辆的正交试验,获得了吸污运行参数对吸污效率和吸污能力的影响规律:影响最显著的因素是吸风口与道床距离L,其次是走行速度v0,最不显著的是吹风口偏角α。根据试验数据进行极差分析,并确定了优选实施方案。
(2)采用多元非线性回归分析法,分别建立了除净率P和可吸煤粉最大粒径D的回归模型。该回归计算模型求得的误差值较小,证明了所建立回归模型的精度良好。在后续车辆调试及工作运行时利用该模型选择合适的运行参数,可降低制造成本,提高工作效率。

