模型法估计电动汽车动力电池健康状态

杨晴霞，李秀青，高建平，马心坦，曹秉刚

(1.河南科技大学a.车辆与交通工程学院；b.金属材料磨损控制与成型技术国家地方联合工程研究中心，河南 洛阳 471023；2.西安交通大学 机械制造系统工程国家重点实验室，陕西 西安 710049)

0 引言

随着纯电动汽车越来越受到人们的关注，锂离子电池作为纯电动汽车的动力来源，由于其具有经济性好、能量密度和功率密度高、续航能力强等特点，深受生产厂家和用户的青睐[1]。电动汽车动力电池健康状态，可为电动汽车的续驶里程估计提供重要信息[2]，同时也可对电池的使用寿命及安全性能进行监测，然而，电池健康状态很难在线实时检测，因此需要对电动汽车动力电池的健康状态进行估计。

常见的电池健康状态(state of health,SOH)估计方法主要分为两大类：物理失效分析法和数据驱动法[3-5]。物理失效分析法需对电池的电化学特性、物理特性有非常深入的了解，常常应用于实验室，很难实现电池健康状态的在线估计。而数据驱动法通过对不同健康状态的电池数据进行采集并分析，可实现电动汽车动力电池健康状态的在线估计。数据驱动法中常用的是模型法[6-7]，即根据可测的电池信息，建立锂电池健康状态预测模型或者依据现有模型估计电池健康状态，可对电池健康状态进行量化分析，因此本文拟采用模型法对电池健康状态进行估计。

常用的锂离子电池模型主要分为电化学模型、经验模型和等效电路模型等[8-10]，其中，等效电路模型是利用电子元件(如电阻、电容、电感等)对电池特性进行描述的一种模型。典型的等效电路模型包括Rint模型、电阻电容(resistance-capacitance，RC)模型等。文献[11]为了对电池荷电状态进行估计，采用改进的等效电路对电池进行建模，所建立的模型可有效且准确地表征电池特性。文献[12]通过建立二阶RC等效电路模型对锂离子电池状态进行估计，所建立的等效电路模型能够准确反映电池动态特性。

综上所述，电池的等效电路模型可准确有效地表征电池特性，因此，本文拟采用模型法，基于锂离子电池等效电路模型，对电池的健康状态进行估计。对不同的锂离子电池模型进行分析，并提出相应的模型参数辨识方法。通过所提出的模型及参数辨识方法对锂离子电池健康状态进行估计，并进行实验验证。

1 锂离子电池模型

考虑到锂离子电池等效电路模型众多，本文选取3种不同精度的电池模型进行分析，包括一阶RC(1-RC)模型、二阶RC(2-RC)模型和分数阶阻抗模型。

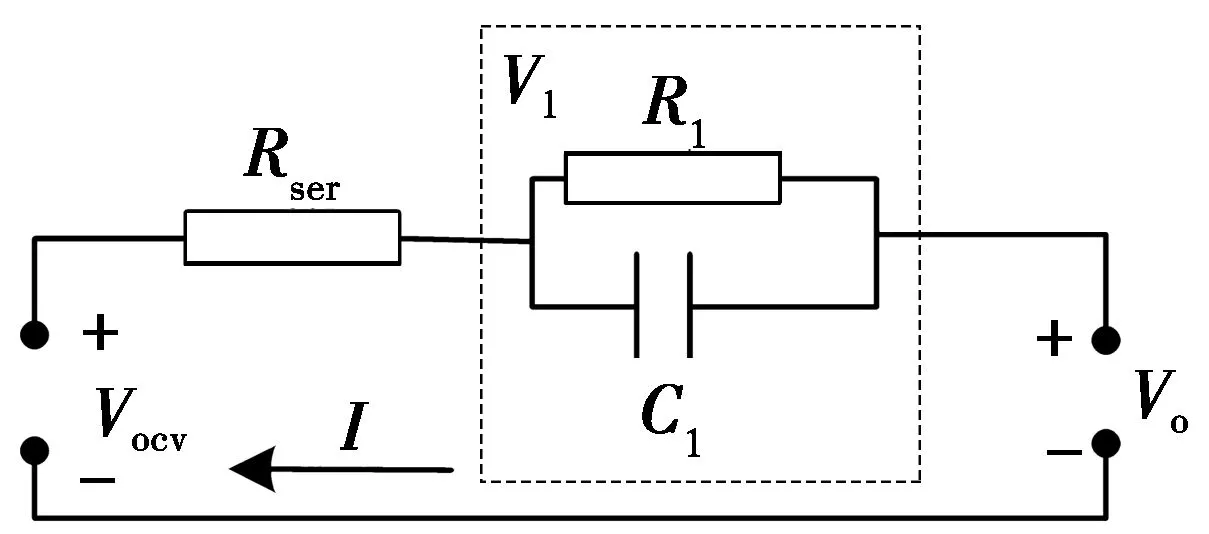
图1 1-RC等效电路模型

1.1 锂离子电池1-RC模型

锂离子电池的1-RC等效电路模型如图1所示，其中:Vocv为电池开路电压，V;Rser为电池欧姆内阻，Ω;Vo为电池工作电压，V;I为电池工作电流，mA;R1、C1和V1分别为1-RC回路的电阻、电容和分电压。

根据电路理论，假设电池放电时的电流I为正，可将1-RC等效电路模型[13]表示为：

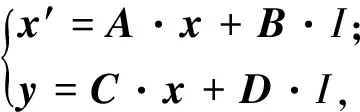
(1)

其中：A=[1/R1C1]；B=[1/C1]；C=-1；D=[-Rser]；x=[V1],x∈R；y=[Vo-Vocv]。

可采用递推最小二乘(recursive least squares，RLS)算法进行参数辨识。

1.2 锂离子电池2-RC模型

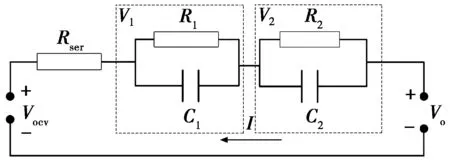
图2 2-RC等效电路模型

锂离子电池的2-RC等效电路模型如图2所示，其中:R2、C2和V2分别为2-RC回路的电阻、电容和分电压。

假设电池放电时的电流I为正，根据电路理论，可将2-RC等效电路模型[12]表示为：

(2)

可采用RLS算法进行参数辨识。

1.3 锂离子电池分数阶阻抗模型

图3 分数阶阻抗模型

锂离子电池的分数阶阻抗模型(fractional impedance model，FIM)[14]如图3所示，其中：R1-CCPE1为电阻-常相位角元件并联组合1，用来表征电池的浓差极化现象；R2-CCPE2为电阻-常相位角元件并联组合2，用来表征电池的活化极化现象。

根据电路原理以及分数阶定义[15-16]，分数阶阻抗模型的等效电路可以表示为：

(3)

其中：V1为电池浓差极化内阻分压，V；α为电池浓差极化分数阶阶数；V2为电池活化极化分压，V；β为电池活化极化分数阶阶数；△α表示分数阶数为α的运算；△β表示分数阶数为β的运算。

将式(3)写为状态空间形式：

(4)

本文所选取的锂电池电化学阻抗模型，其内部可变参数较多，很难单纯地应用最小二乘法进行参数辨识。为对所选取的模型进行参数辨识，可建立一个等效电压追踪系统，其建模参照文献[17]，如式(5)所示：

(5)

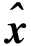
根据随机原理和G-L分数阶定义，同样将等效电压追踪系统离散化，其离散化模型如下所示：

(6)

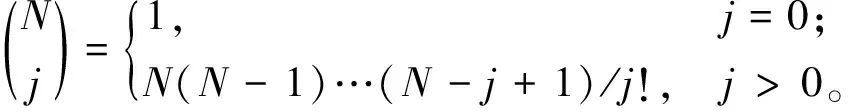
在对建立的分数阶阻抗模型进行参数辨识时，最小二乘遗传算法(least squares genetic algorithm，LSGA)的目标函数J(θ)设定为求取目标方程的最小值，目标函数如式(7)所示：

(7)

2 电池健康状态估计及实验分析

为了对电动汽车动力电池健康状态进行估计，选取型号为松下NCR18650的特斯拉Model S动力电池作为实验对象，该类型电池为三元锂离子动力电池。首先，基于锂离子电池加速老化实验对不同模型的电池参数进行辨识，然后对不同模型所获得的电池内阻与电池健康状态之间的关系进行对比分析，从而提出一种基于模型的电池健康状态估计方法。在实验过程中，对数组电池进行测试，测试结果基本能够保持一致，因此选取其中2组具有代表性的电池数据进行分析。

2.1 基于1-RC模型内阻的电池健康状态估计与分析

对1-RC模型采用RLS法进行内阻参数辨识，并将所获得的电池欧姆内阻与电池健康状态进行线性拟合，结果如图4所示。

(a) 1-RC模型电池健康状态线性拟合

(b) 1-RC模型电池健康状态估计误差

图4 基于1-RC模型电池内阻的电池健康状态估计

分析图4a可知：当利用加速老化实验充电过程得到的1-RC模型电池内阻增大时，电池的实际健康状态逐渐降低。也就是说，电池健康状态与利用加速老化实验充电过程得到的1-RC模型电池内阻之间可能存在一定的线性关系。采用线性拟合法对其拟合，根据拟合结果可知该方法理论上可实现电池健康状态的在线估计。分析图4b可知：采用基于1-RC模型电池内阻对电池健康状态进行线性拟合估计，其估计误差为-3.0%～1.5%，也就是说在电池充电过程中，基于1-RC模型进行在线辨识得到的电池内阻，可对电池健康状态进行在线估计，进一步验证了文献[18]所提出的电池内阻可用于估计锂离子电池健康状态这一结论。

2.2 基于2-RC模型电池内阻的电池健康状态估计与分析

对2-RC模型采用RLS法进行内阻参数辨识，并将所获得的电池欧姆内阻与电池健康状态进行线性拟合，结果如图5所示。

(a) 2-RC模型电池健康状态线性拟合

(b) 2-RC模型电池健康状态估计误差

图5 基于2-RC模型电池内阻的电池健康状态估计

分析图5a可知：当利用加速老化实验充电过程得到的2-RC模型电池内阻增大时，电池的实际健康状态逐渐降低。采用线性拟合法对其进行拟合，根据拟合结果可知该方法理论上可实现电池健康状态的在线估计。分析图5b可知：采用基于2-RC模型电池内阻对电池健康状态进行线性拟合估计，其估计误差为-2.5%～1.5%，该误差范围比采用1-RC模型的估计误差范围更小，也就是说在电池充电过程中，基于2-RC模型进行在线辨识得到的电池内阻同样可以用于电池健康状态在线估计，且估计精度比基于1-RC模型的更高。

2.3 基于分数阶阻抗模型电池内阻的电池健康状态估计与分析

对FIM采用LSGA法进行内阻参数辨识，并将所获得的电池欧姆内阻与电池健康状态进行线性拟合，结果如图6所示。

(a) FIM电池健康状态线性拟合

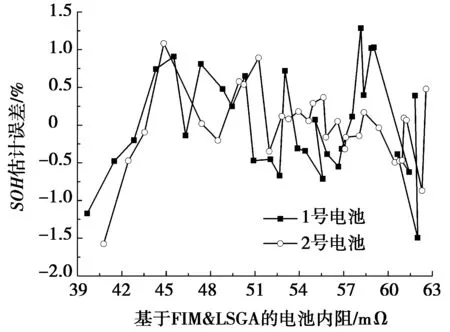
(b) FIM电池健康状态估计误差

图6 基于分数阶阻抗模型电池内阻的电池健康状态估计

分析图6a可知：当利用加速老化实验充电过程得到的分数阶阻抗模型电池内阻增大时，电池的实际健康状态逐渐降低。采用线性拟合法对其拟合，根据拟合结果可知该方法理论上可实现电池健康状态的在线估计。分析图6b可知：采用基于FIM电池内阻对电池健康状态进行线性拟合估计，其估计误差为-2.0%～1.5%，该误差范围比基于2-RC模型的误差范围更小，也就是说，在电池充电过程中，基于FIM进行在线辨识得到的电池内阻可以更加有效地对电池健康状态进行在线估计，且估计精度比基于1-RC模型和2-RC模型的精度更高。

3 结束语

本文对基于电池模型的电池内阻健康状态估计进行了研究，针对现有1-RC模型、2-RC模型以及分数阶阻抗模型，提出相应的参数辨识方法，对处于不同健康状态下的电池内部参数进行在线辨识，对电池内阻在电池老化过程中的变化情况进行分析。采用不同模型以及参数辨识方法得到的电池内阻均可对电池健康状态进行在线估计，估计误差在3%以内，且随着模型精度的提高，基于模型内阻参数的电池健康状态在线估计也越准确，在大数据技术快速发展的背景下，为电池健康状态在线估计的后续研究提供了理论基础。