混合动力汽车模式切换协调控制

王 卉，左言言，孙 瑞，臧九余

(江苏大学 振动噪声研究所，江苏 镇江 212013)

0 引言

混合动力汽车配有两个及以上的动力源，根据行驶工况和需求功率的不同，各动力源的组合方式发生相应的变化[1]。由于发动机和电机存在明显的动态响应差异，模式切换过程中存在动力不足或输出转矩波动过大的情况，由此引起的瞬态冲击会对整车的行驶平顺性和乘坐舒适性产生影响[2]。

近年来，国内外学者对混合动力汽车模式切换过程的动态协调控制做了大量研究。文献[3]针对离合器变速器换挡的情况，提出了发动机转矩开环+发动机转矩动态估计+电动机转矩补偿的控制算法体系。文献[4]针对复合功率分流的混合动力轿车模式切换过程中汽车平顺性问题，提出了一种无扰动模式切换控制策略，协调各动力源转矩，保证不同模式间的平顺切换。文献[5]针对模式切换时离合器结合过程，设计了基于H∞鲁棒控制和基于L2增益鲁棒控制的分层控制器，并通过试验验证了控制器的鲁棒性和有效性。文献[6]针对某种轻度混合动力汽车建立了发动机转矩观测器，可以对发动机转矩波动进行实时计算，并利用电动机转矩抵消发动机的转矩脉冲，改善了车辆的平顺性。文献[7]将模式切换控制问题简化为对离合器结合过程的控制，通过对离合器结合压力的开环控制，实现对目标离合器转矩的跟随，可以减少模式切换的冲击度和离合器滑磨功。文献[8]从电机控制的角度制定模式切换控制策略，以降低模式切换时因冲击过大引起的车辆振动和噪声。文献[9]提出了基于车轮转速差比例-积分-微分(proportion integration differentiation，PID)控制的电机转矩补偿控制方法，解决了两种动力源间的动态协调控制问题。文献[10]分别基于μ综合方法提出了发动机侧和电机侧的鲁棒控制器，该控制器考虑了离合器转矩扰动对系统的影响，并将前馈控制和反馈控制相结合，实现了两动力源端的解耦控制，提高了整车性能。

以上研究对象多为具有离合器、传统变速器的并联式混合动力系统，主要考虑离合器执行机构动态特性对切换控制的影响，而本文的研究对象是双行星排式混合动力汽车动力系统，该系统无离合器机构，因此动态控制问题也有所差异。本文针对纯电动模式切换至混合驱动模式中发动机启动过程，提出了基于模型预测控制(model predictive control,MPC)的转矩协调控制策略，设计相应的模型预测控制器，减少模式切换中各动力源转矩不协调引起的瞬态冲击，确保模式切换时车辆的平顺性和舒适性。并通过仿真平台，验证了模式切换过程中整车冲击度的改善情况。

1 动力系统的结构与分析

图1是研究的双行星排式混合动力系统构型图，该系统包括前排动力分配行星齿轮机构和后排电机减速行星齿轮机构。该动力系统可以根据行驶需求，在发动机和电机之间进行灵活地切换和组合，实现纯电动模式、发动机单独驱动模式和混合驱动模式等多种工作模式。动力系统的主要参数见文献[11]。

1.1 动力学模型

为了更清楚地分析该混合动力系统的动力传递情况，采用隔离法分别对前行星排、后行星排和系统输出3部分建立动力学模型。图2为动力系统动力传递线框图。

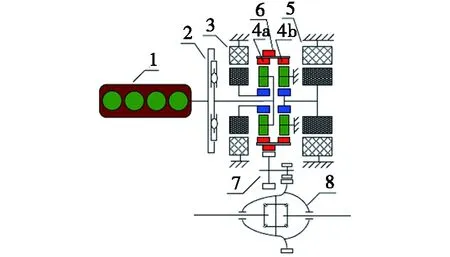
1.发动机;2.扭转减振器;3.电机MG1;4a.前行星排PG1;4b.后行星排PG2;5.电机MG2;6.复合齿圈;7.主减速器齿轮;8.驱动桥。

图1 双行星排式混合动力系统构型图

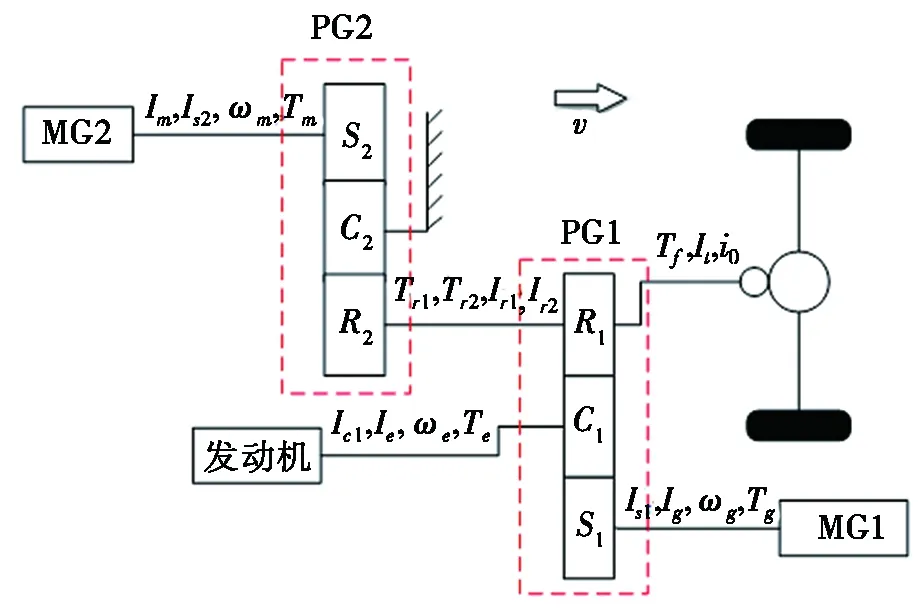
图2 动力系统动力传递线框图

对于前行星排机构PG1，发动机和前排行星架相连，电机MG1和太阳轮相连，系统转矩由前排齿圈输出。忽略摩擦损失和黏滞损失，根据欧拉定律、行星齿轮机构和动力源的连接关系，得到前行星排的输入输出关系：

(1)

其中：I、R、T、ω分别为转动惯量、半径、转矩和角速度；下标s1、c1、r1分别代表前行星排的太阳轮、行星架和齿圈；下标e、g分别代表发动机和电机MG1；F1为前行星轮的内力。

对于后行星排机构PG2，后排行星架与壳体固定，电机MG2与后排太阳轮相连，其转矩经减速增扭后由复合齿圈输出。同样地，得到后行星排输出转矩Tr2与输入转矩Tm的关系：

(2)

其中：下标m、s2和r2分别表示电机MG2、后排太阳轮和后排齿圈。

对于系统输出部分，发动机转矩和电机MG2的转矩由复合齿圈输入到主减速器输入端，驱动车辆行驶，故系统输出部分的动力学关系如下所示：

(3)

其中：nt、It、Rt分别为车轮数、车轮转动惯量和车轮半径；a为车辆纵向的加速度；v为车速；i0为主减速器传动比；Tf为车辆行驶过程中受到的阻力矩；Tf0为车辆总的制动力矩；fr为滚阻因数；ρ为空气密度；A为迎风面积；CD为空阻系数。

至此，由式(1)～式(3)便可以描述出该混合动力汽车动力系统的动力传递情况。

1.2 动态协调问题分析

以车辆纵向冲击度J作为模式切换效果的评价指标[12]：

(4)

基于上文的动力学模型，即式(1)～式(3)，可推导出三动力源转矩与系统输出轴角速度的关系，对其进一步改写，得到各动力源转矩变化与系统纵向冲击度之间的关系：

(5)

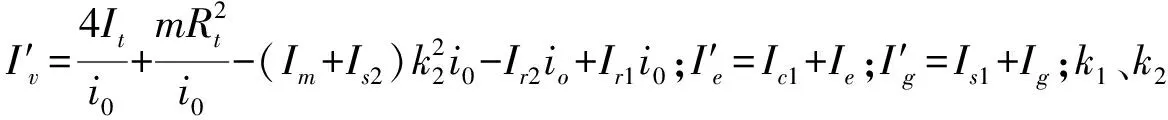
2 基于模型预测的转矩协调控制策略

本文针对模式切换中发动机快速启动引起系统冲击的问题，基于MPC方法设计了两者兼顾的转矩协调控制策略，在保证发动机能快速启动的前提下，实现3个动力源的转速转矩协调，从而实现不同模式间的平顺切换。MPC是一种在线滚动优化控制算法，具有适用性广、鲁棒性强等特点，可用来解决当前时刻的控制命令与未来时刻系统响应不协调的问题[13-14]。其基本原理的介绍请参阅文献[15-16]。

2.1 电机MG1转矩协调控制

基于上文的分析，电机MG1转矩协调的控制目标是使发动机快速启动，并且尽可能减少由电机MG1转矩变化引起的系统负向冲击。

由前文系统动力学模型(见式(1))以及行星齿轮机构的转速关系[17]，得到发动机启动过程系统的状态方程：

(6)

以发动机转速为系统状态变量x，电机MG1的转矩为系统控制输入量u1，未来时刻发动机的转速为系统控制输出量y，建立发动机启动过程的状态空间表达式：

(7)

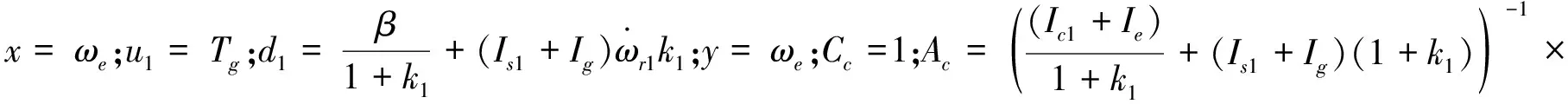
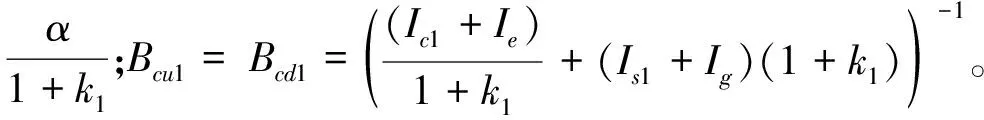
参考现代控制理论，以采样周期Ts对式(7)进行离散化处理，得到发动机启动过程系统状态空间的离散化模型：

(8)

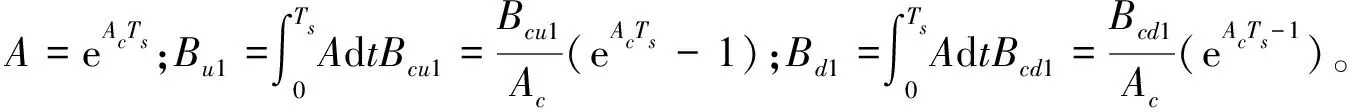
为了减少稳态误差，对式(8)采用差分运算并改写成增量模型：

(9)

其中：△x(k)=x(k)-x(k-1)；△u1(k)=u1(k)-u1(k-1)；△d1(k)=d1(k)-d1(k-1)。

此外，根据模型预测控制的基本原理，定义本文系统的控制时域Nc小于预测时域Np，且假设系统干扰△d1在预测时域内保持不变，即：

△d1(k+i)=0,i=1,2,…,Np-1。

(10)

则系统的预测模型可由式(9)递推得到：

Yc(k+i|k)=Sx△x(k)+Icy(k)+Su△U1(k+j|k)+Sd△d1(k)，

(11)

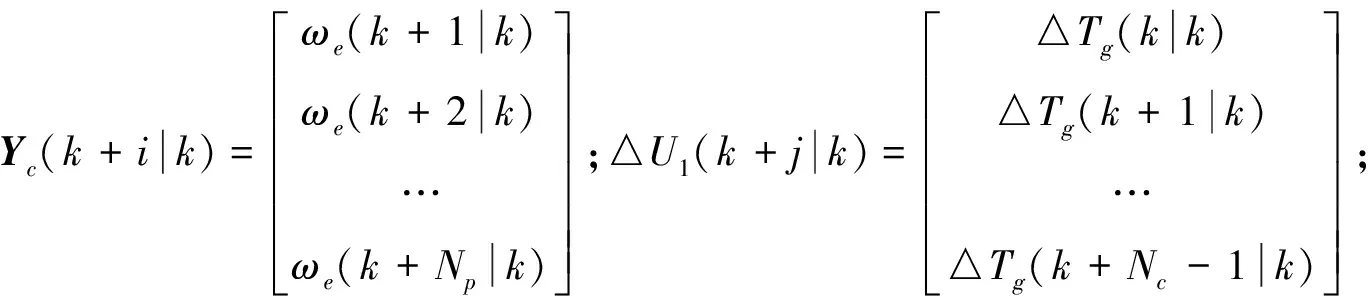
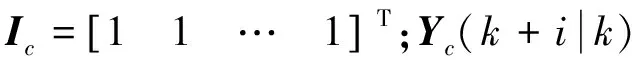
考虑系统的控制要求和各部件的性能约束，建立优化目标函数和约束函数。主要控制目标是使发动机快速启动，并且在模式切换过程中整车冲击度尽可能小：

(12)

其中：Re(k)为发动机的目标转速；Q和R均为正加权矩阵；ρ为权重系数；ε(ε>0)为松弛因子；ωe min、ωe max分别为发动机角速度的最小限值和最大限值；△Tg min、△Tg max分别为电机MG1转矩变化量的最小限值和最大限值；Tg min、Tg max分别为电机MG1转矩的最小限值和最大限值。优化目标中的第1项考察发动机转速对目标转速的跟踪能力，第2项控制电机MG1转矩平稳变化，末项保证目标函数在任意时刻均有可行解。

利用二次规划方法对目标函数进行求解，得到满足上述要求的最优控制序列，序列中的第1个值就是当前时刻系统的控制输入量，即电机MG1的转矩变化量。

2.2 电机MG2转矩补偿控制

由冲击度的分析可知，发动机启动过程中，电机MG1带动发动机启动将输出正向转矩，从而引起系统负方向的冲击。因此，对于电机MG2的转矩控制要求是，在满足整车需求转矩的同时，对电机MG1引起的转矩脉冲进行主动补偿，进一步降低系统冲击。

结合式(2)和式(3)，得到电机MG2与系统输出转矩间的关系：

(13)

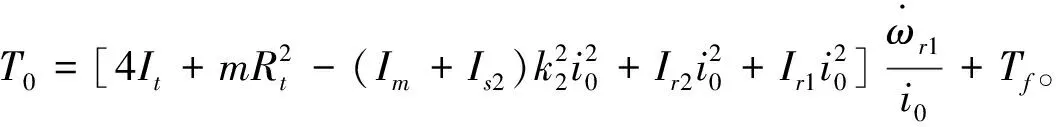
以发动机转速为系统状态变量x，电机MG2的转矩为系统控制输入量u2，系统的状态方程可表示为：

(14)

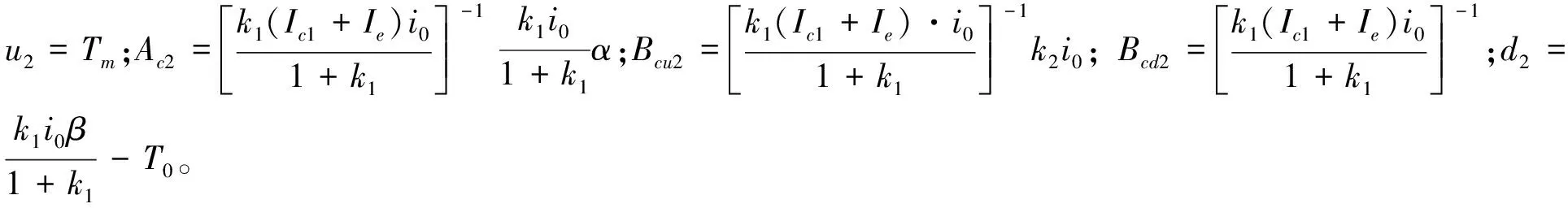
同样地，以采样周期Ts对式(14)进行离散化处理并采用增量式控制，得到系统增量方程：

△x(k+1)=A2△x(k)+Bu2△u2(k)+Bd2△d2(k)，

(15)

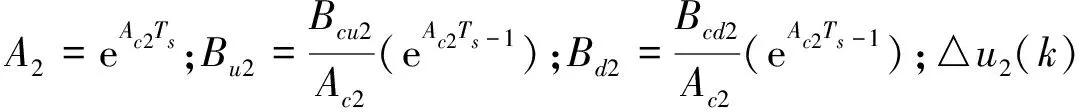
基于式(12)的优化计算结果可以确定电机MG1的转矩增量△u1(k)，将其带入式(9)可以得到系统下一时刻的状态变量△x(k+1)obt，再结合式(15)即可求得满足上文优化目标要求的电机MG2的转矩增量△u2(k)obt：

(16)

由该方法得到的电机MG2转矩增量不仅可以满足整车需求转矩的要求，还可以有效地减少发动机启动过程中系统状态变化对系统输出转矩的影响，很好地补偿电机MG1输出正向转矩引起的系统负向冲击，实现良好的补偿作用。

2.3 模型预测控制器的设计

基于模型预测算法设计模型预测控制器，图3为MPC控制器的结构图。将MPC控制器放置在车辆控制策略模块中，车辆以纯电动模式行驶时，各动力源转矩分配由稳态能量管理策略决定，当检测到模式切换请求且需要启动发动机时,动态控制策略的开始标识符置1，MPC控制器开始作用，进入发动机启动过程的瞬态控制模式。MPC控制器根据系统当前状态预测被控系统的未来状态，控制器通过求解优化问题获得最优控制量，即电机MG1和电机MG2的转矩变化值，将最优控制序列的第1个元素作用于控制系统中，下一时刻重复执行上述操作，实现在线滚动优化。

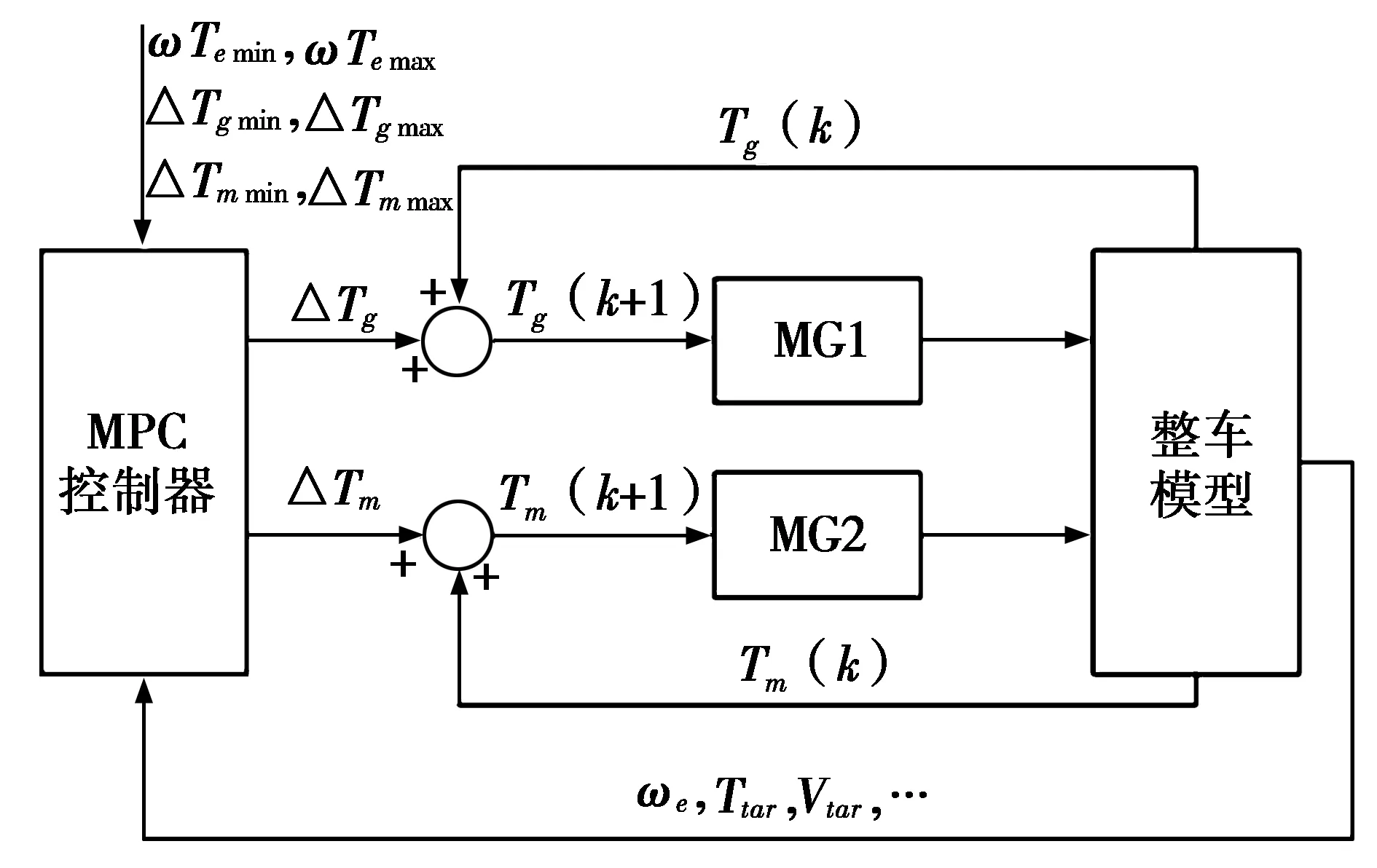
图3 MPC控制器的结构图

3 仿真验证

对车辆由纯电动模式向混合驱动模式切换的动态协调控制进行仿真验证，将MPC控制方法的仿真结果与PID控制法、无协调控制的仿真结果进行对比。

图4为模式切换过程中3种控制方法下电机的转矩变化情况。由图4a可知：无协调控制时，在接收到模式切换命令后，电机MG1缓慢输出转矩带动发动机启动；而在闭环PID控制方法下，当接收到模式切换指令时，电机MG1迅速增大转矩后维持恒转矩输出；相比之下，MPC控制方法控制电机MG1转矩的变化比较平稳。由图4b可知：无协调控制时，电机MG2转矩突降以响应自身需求转矩的要求；PID控制方法下，由于PID控制未能准确估计发动机启动过程中的转矩输出情况，受系统需求转矩的影响，电机MG2转矩出现较大波动；而MPC控制方法下，电机MG2的转矩由MPC控制器根据系统当前状态预测得到，呈现先平稳上升后缓慢下降的趋势。

图5为模式切换过程中3种控制方法下发动机的转速、转矩变化情况。由图5a可知：PID控制方法下发动机启动最快，经0.3 s便能达到怠速转速，而无协调控制时发动机启动最慢，大约需要0.7 s。与PID控制方法相比，MPC控制方法下发动机启动时间有所增加，约0.4 s,但该时间仍满足实际需求。由图5b可知：相比于其他两种方法，MPC控制方法下发动机转矩变化最平稳。

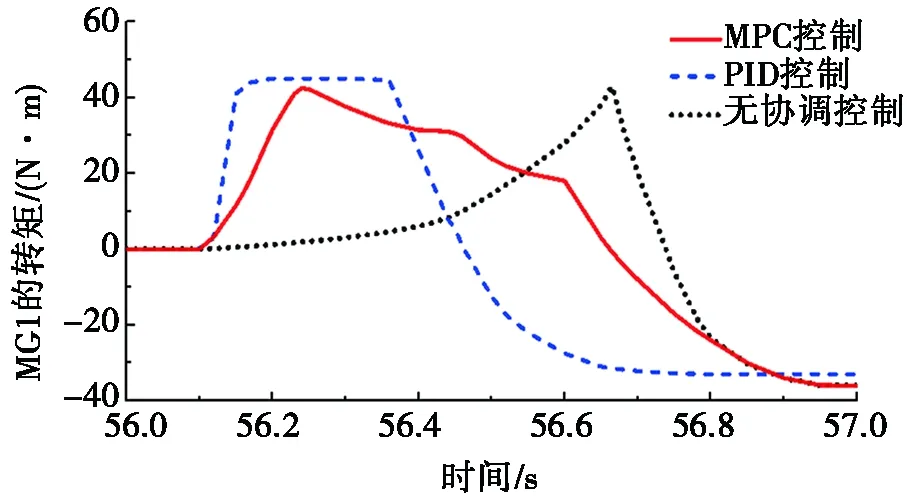
(a) 电机MG1的转矩变化

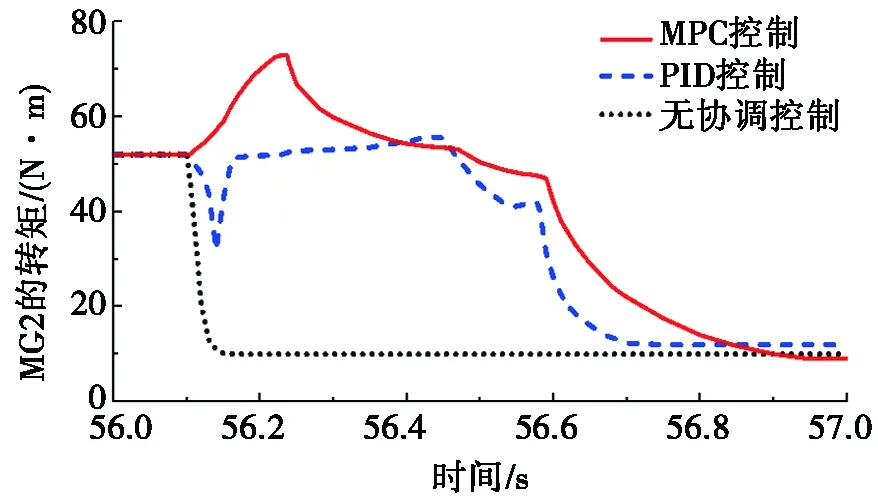
(b) 电机MG2的转矩变化

图4 电机的转矩变化

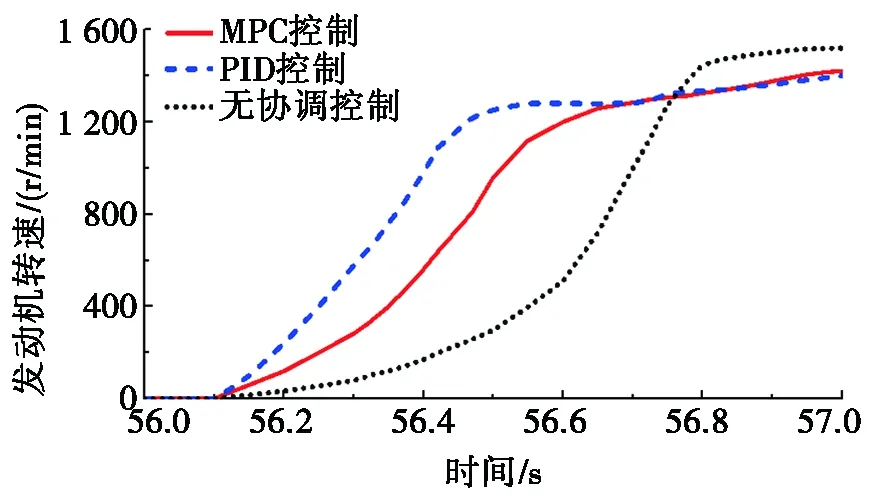
(a) 发动机的转速变化

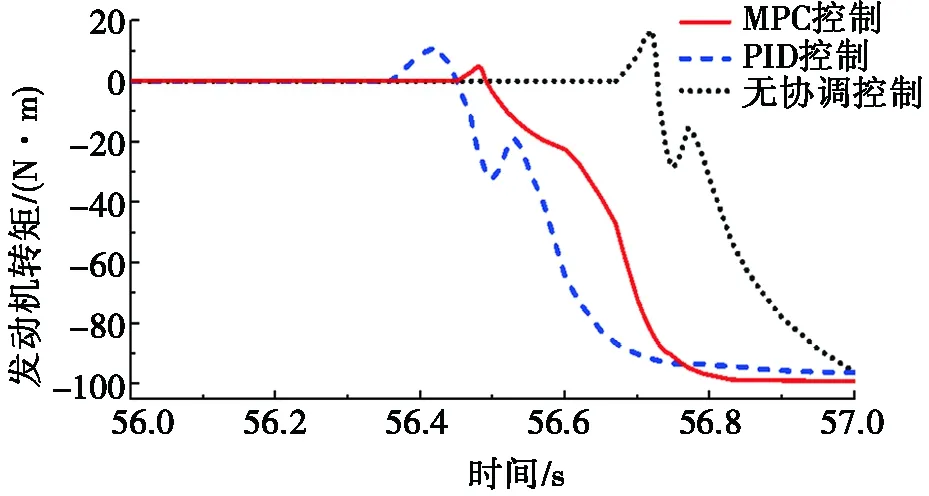
(b) 发动机的转矩变化

图5 发动机的转速、转矩变化

对比3种控制方法下整车冲击度的变化和车速跟随情况，分别如图6和图7所示。由图6可知：模式切换初始时刻，PID控制方法下出现了较大的负向冲击；当发动机达到点火转速并开始响应目标转矩时，由于PID控制未能准确估计发动机输出转矩值，两动力源转矩不协调，系统纵向出现较大的正冲击，系统平顺性有待提高。无协调控制时，电机MG2的转矩迅速下降至目标转矩附近，车辆在模式切换时刻出现负方向的冲击。相比之下，MPC控制方法使电机MG2与电机MG1的转矩相适应，利用电机MG2转矩补偿电机MG1输出的正向转矩，减少了模式切换时刻系统的负向冲击。同样地，当发动机达到点火转速并有转矩输出时，电机MG2能有效协调发动机转矩变化，主动调节自身转矩的输出，减少了发动机启动引起的系统纵向的冲击。此外，由图7可知：无协调控制时由于发动机启动过程较长，系统输出转矩不足，车速在较长一段时间内无法满足驾驶需求；而PID控制方法和MPC控制方法能保证实际车速与目标车速具有较好的一致性，且MPC控制方法的车速偏差更小。3种控制方法下，整车冲击度绝对值的最大值对比以及车速跟随情况的对比如表1所示。

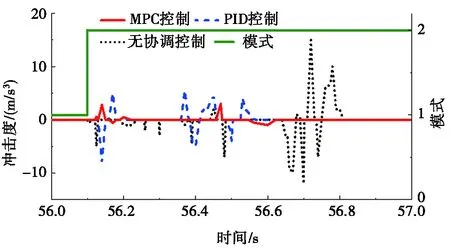
图6 冲击度对比

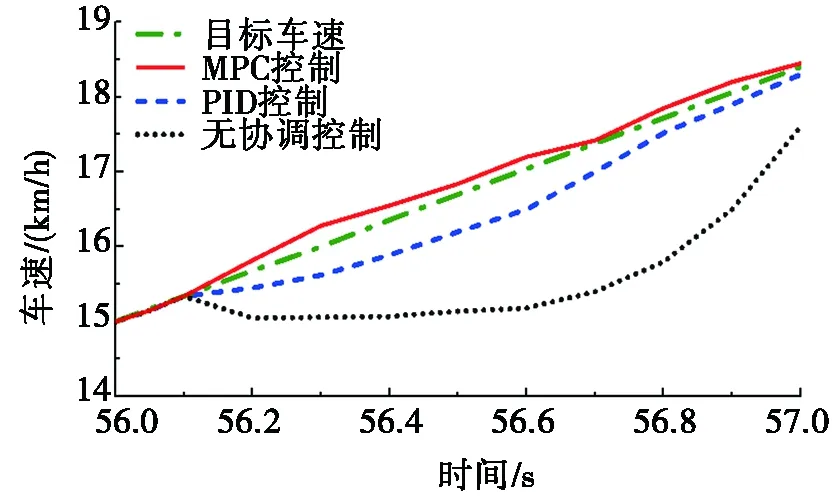
图7 车速跟随情况对比

表1 3种控制方法结果对比

由表1可知：相比于PID控制和无协调控制，本文设计的MPC控制器在模式切换过程中可以有效地降低模式切换引起的系统纵向冲击，将其冲击度峰值控制在3 m/s3左右，符合汽车行业中冲击度的推荐值[18]。基于MPC算法的控制方法，实现了对需求车速的良好跟踪，在提升车辆平顺性的同时也满足了车辆动力性的要求。

4 结论

本文提出的模式切换协调控制方法，能保证系统各部件在切换过程中相互配合、协调运作。相比于传统的PID控制和无协调控制，基于模型预测控制的方法在满足发动机快速启动要求的前提下，有效减小了模式切换时车辆最大冲击度，且整个模式切换过程车速跟随情况良好，保证了模式切换过程中车辆的平顺性和动力性。