流量差异和管径突变对立管流动状态的影响

范玉斌，王卫强，秦国庆，庄正刚

（1.辽宁石油化工大学石油天然气工程学院，辽宁抚顺113001；2.延长石油（集团）有限责任公司，陕西西安710000）

随着海洋油气田的开发，深海多相混输技术和集输管网已成为海洋油气开发及输送的最主要方式，但是这种输送方式对流动保障技术提出了越来越高的要求[1-4]。海洋集输管网包括水平管、倾斜管、立管等不同管型及不同的组合形式，目前较为常用的管型为T型管。根据所采用的工艺流程的不同，可能存在各种问题：不同分支管线的流量差异，卧管、立管的管径突变以及立管自身的管径突变可能带来流动保障方面的问题；在生产末期气液总流量较小时，极易形成严重段塞流[5]，从而导致油井减产、管道振动等问题。相关学者研究气液两相流的结果发现，气液两相物性、表观速度、管道物性及形状对流型的影响很大[6-9]。D.V.Essendelft等[10]利用不同尺寸的管道，通过改变气液相表观速度，得到了不同的流型；T.S.Zhao等[11]对三角形管道的流型进行了研究，结果表明流型受水力半径的影响；H.Liu等[12]对方形管道的流型进行了研究，并测得了搅拌流型、泡状流型、环状流型、段塞流型和段塞-弹状流型。因此，研究分支流量差异、管径突变等问题对立管流动状态的影响，对保证海洋油气的安全及顺利运行有重要的意义。

1 模型的基本参数及假设条件

根据某深海油气田的实际数据进行计算，数值计算所采用的油品组成见表1。PVTsim软件生成所需要的流体属性，稳产时的含水率（摩尔分数，下同）为10.00%。

表1 数值计算所采用的油品组成

设置OLGA软件参数[13]：管道内径为0.12 m，管道内壁粗糙度为5×10－5；管材的比热容为500 J/(kg·℃)，导热系数为50.00 W/(m·℃)，密度为780.0 kg/m3；保温层材料的密度为800.0 kg/m3，比热容为500 J/(kg·℃)，导热系数为0.18 W/(m·℃)。

海洋T型集输管网数值计算基础模型见图1。水平管段（管A和管B）和立管（管C）的管径为0.06 m。

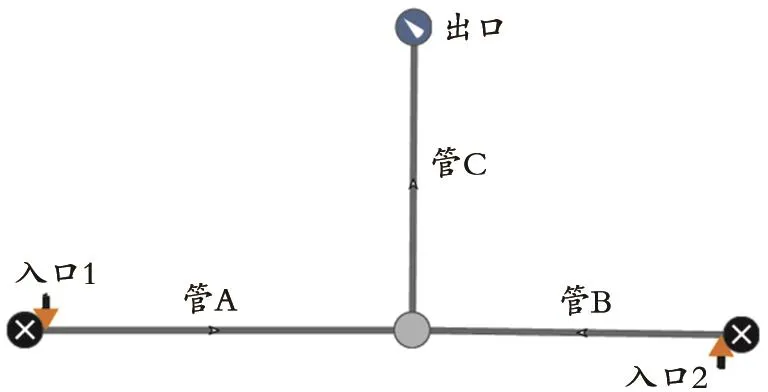
图1 海洋T型集输管网数值计算基础模型

设置边界条件：入口为质量源，模拟时设定温度、产液量、气油物质的量比、含水率；出口为压力边界，输入出口处压力。

结构参数：水平管段（管A和管B）的长度为2 000 m，立管（管C）的高度为2 000 m，油相的密度为900.0 kg/m3，气相的密度为 717.4 kg/m3。

2 结果与分析

在水平管段入口处总流量Q不同的条件下，研究了立管沿程液相流量、立管沿程温度、立管沿程压力及持液率，结果如图2所示。

图2 Q对立管管内流动参数的影响

从图2（a）可以看出，在给定的入口温度（70℃）、出口压力（1.5 MPa）、管径（0.06 m）和含水率（10.00%）的条件下，随着水平管段入口处总流量Q的增大，立管沿程液相流量增大，并且立管沿程各点的液相流量基本不变；立管的流量略小于两条水平管段总流量；与水平管段入口处总流量较小的情况相比，当水平管段入口处总流量Q=0.030 m3/s时，立管顶部管段h＞1 300 m处沿程液相流量有明显减小，立管内流动状态由层流转变为泡状流。

从图2（b）可以看出，在给定的入口温度（70℃）及水平管段入口处总流量Q不同的情况下，立管沿程温度分布表现出不同的规律。在水平管段入口处总流量Q不同时立管底部入口温度不同，因此立管沿程温度分布存在较大差异。但是，在水平管段入口处总流量较大（Q=0.005～0.030 m3/s）的条件下，水平管段入口处总流量不同时立管沿程降温速率基本相同，同时以层流向泡状流转变处为分界点，两个管段的温降速率表现出微小差异[14]。

从图2（c）可以看出，随着水平管段入口处总流量Q的增大，立管沿程压力下降速率逐渐增大；在Q=0.001 m3/s和Q=0.005 m3/s时，立管沿程压力基本相等。

从图2（d）可以看出，当改变水平管段入口处总流量Q时，持液率随之发生变化；在Q=0.001～0.005 m3/s和Q=0.010～0.030 m3/s的两个阶段，持液率的变化明显不同；在Q=0.001 m3/s和Q=0.005 m3/s时出口处持液率相等，在Q=0.010 m3/s和Q=0.030 m3/s时出口处持液率相等，并且大流量下出口处持液率明显大于小流量下出口处持液率。结合流型分析可知，当水平管段入口处总流量Q增大到一定值时，立管内的流动状态必然完全转变为层流，此时立管内各点的持液率也必然等于1，也就是说检测不到纯气相的存在[15]。

2.1 Q对立管管内流动状态的影响

在水平管段（管A）入口总流量QA为0.001 m3/s的条件下，改变管B入口总流量QB，研究了相关参数的变化规律，结果如图3所示。从图3可以看出，在管A的入口总流量QA不变的条件下，随着管B的入口总流量QB的增大，立管管内流动参数的变化规律与图2相似[16]。

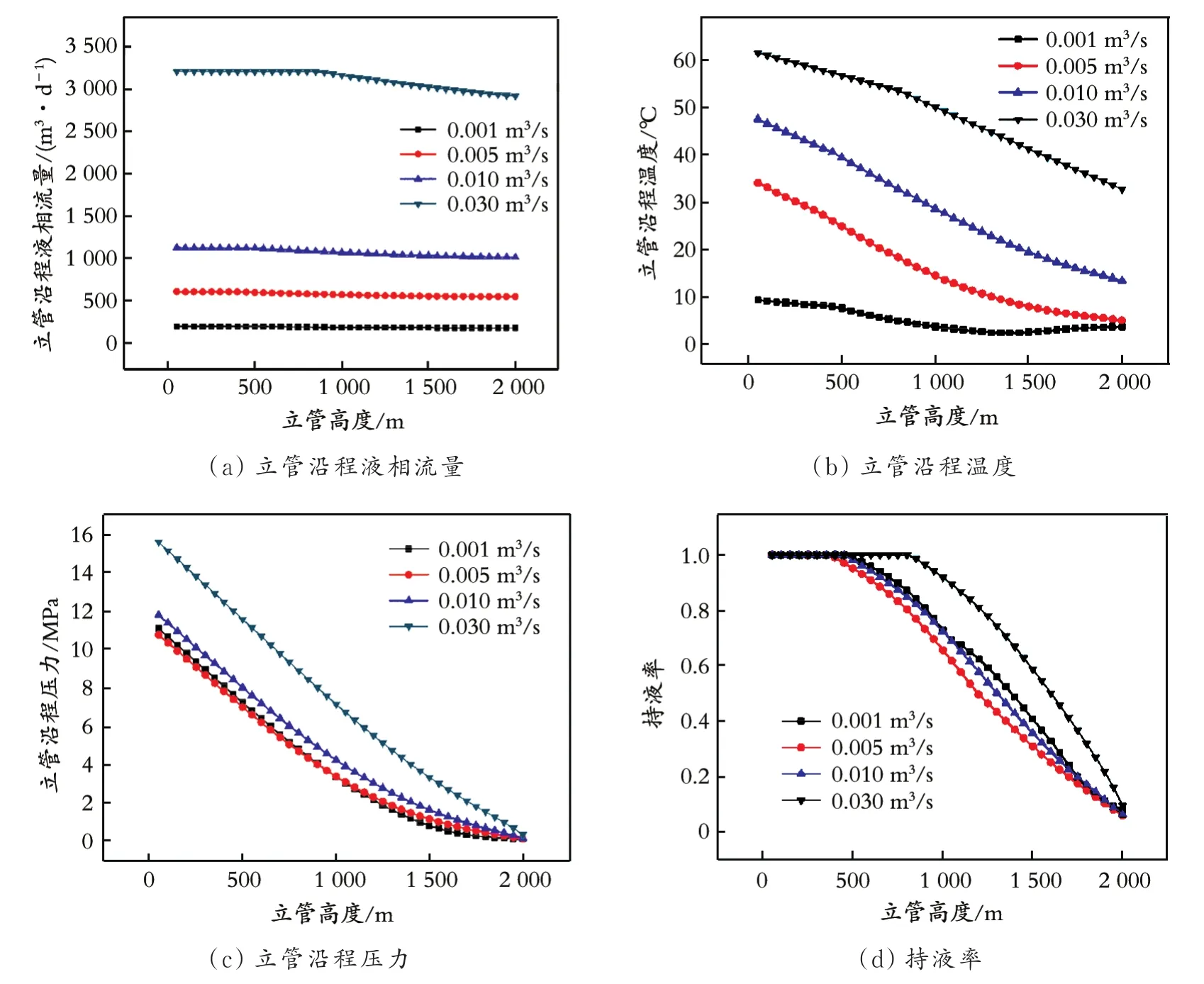
图3 QB对立管管内流动参数的影响

2.2 卧管-立管管径差异对立管管内流动状态的影响

设置管A和管B的管径及流量，D=DA=DB=0.06 m，Q=QA=QB=0.001 m3/s，改变立管管径，研究了立管管内相关参数的变化规律，结果如图4所示。

从图4（a）可以看出，在给定的入口温度（70℃）、出口压力（1.5 MPa）、水平管段管径（0.06 m）、水平管段入口处总流量（Q=0.001 m3/s）和含水率（10.00%）的条件下，随着立管管径的增大，立管沿程液相流量呈3个不同的特征：当DC=0.03 m时，随着立管管径的增大，立管沿程液相流量先基本保持不变然后迅速减小，说明发生了流型的转变[17]；当DC=0.06～0.12 m时，立管沿程液相流量的分布规律与DC=0.03 m时相似，但是从流量的变化情况可以看出流型转变的位置发生了改变；当DC=0.24 m，且立管高度h＞1 500 m时，可能存在流型之间的交互变化，在该管段立管沿程液相流量可能存在极小值。

从图4（b）可以看出，立管管径不同时立管沿程温度分布各不相同，立管沿程温度下降速率的变化规律与立管沿程液相流量的变化也呈不同规律。虽然在立管管径不同时立管沿程液相流量呈相同特征，但是其流型的变化却不尽相同[18]。

从图4（c）可以看出，立管管径对立管管道压力的分布影响明显：立管的管径越大，其压降下降速度越小，下降速率比较平稳，与管内流动状态无关。

从图4（d）可以看出，持液率的变化规律与管道液相流量的变化规律一致。

图4 立管管径对立管相关参数的影响

2.3 立管管径的突变对立管内流动状态的影响

设置管A和管B的直径及入口处总流量，D＝DA＝DB＝0.06 m，Q＝QA＝QB＝0.001 m3/s，在立管高度h＝0～1 000 m和h＝1 000～2 000 m内设置不同的管径，研究了立管管径的突变对相关参数的影响，结果如图5所示。图5中，0.24 m＋0.12 m表示立管高度h=0～1 000和h=1 000～2 000 m内的管径分别为D1＝0.24 m和D2＝0.12 m，以此类推。

图5 立管管径的突变对立管内流动状态的影响

从图5（a）可以看出，在给定的入口温度（70℃）、出口压力（1.5 MPa）、水平管段管径（0.06 m）、入口处总流量（Q=0.001 m3/s）和含水率（10.00%）的条件下，当立管管径突变情况不同时，立管沿程液相流量的变化规律也不同：在层流范围内，立管沿程液相流量基本保持不变；在泡状流范围内，立管沿程液相流量迅速减小；在段塞流范围内，立管沿程流量基本保持不变。从图5（a）还可以看出，当立管的最小管径Dmin相同时，立管沿程液相流量分布基本相同；最小管径越小，在泡状流区域立管沿程液相流量下降也越快。

从图5（b）可以看出，当立管管径突变情况不同时，立管沿程温度分布也不同。当最小管径较小时（Dmin＝0.03 m），在流型转变过程中立管沿程温度变化不明显；当立管的最小管径Dmin相同时，立管沿程温度分布基本相同，并且最小管径Dmin越小，在泡状流区域沿程温降越大。

从图5（c）可以看出，立管的最小管径Dmin越小，立管沿程压降越大。

从图5（d）可以看出，持液率与立管沿程液相流量变化规律呈很好的一致性。

3 结 论

（1）随着水平管段入口处总流量Q的增大，立管沿程液相流量、持液率、立管沿程温度分布规律在层流向泡状流转变前后明显不同，而立管沿程压力分布与立管管内的流动状态无关。

（2）当水平管段A的入口流量QA＝0.001 m3/s时，随着水平管段B的入口流量QB的增大，立管管内流动状态受水平管段总流量Q的影响，与其分支管段的流量无明显关系。

（3）当水平管段管径D＝DA＝DB＝0.06 m时，在立管管径DC为0.03 m、0.06～0.12 m和0.24 m的条件下，立管沿程液相流量、立管沿程温度及立管沿程压力分布的变化规律存在明显的差异；与立管沿程压力分布不同的是，立管沿程液相流量和立管沿程温度分布受管内流动状态的影响。

（4）当水平管段管径保持不变时，立管管内流动参数的变化主要与其最小管径有关：在不同的立管管径组合下，当最小管径相同时，其流动参数均相同；最小管径越小，相关参数的变化程度越大。