风载荷作用下浮顶储罐的屈曲模态分析

吴宛津，张巨伟

（辽宁石油化工大学机械工程学院，辽宁抚顺113001）

储罐作为存储液体和气体的密封容器，在石油化工等领域是必不可少的。然而，储罐面临许多自然灾害问题，强风天气、地震晃动等环境对储罐的影响都不可忽视。在存在风力的情况下，储罐罐壁整体会发生滑移，在强风的作用下储罐罐壁甚至会发生屈曲失效的现象[1]。因此，风载荷已经成为大型立式储罐安全设计方面需要考虑的重要因素。只有提高储罐的安全性能，储罐才能安全地储存石油天然气，如果储罐泄漏，不仅破坏生态环境，而且给经济带来巨大影响[2]。国内外的众多学者主要以圆柱壳体结构的储罐为研究对象，以瞬时风压和极限风压为影响因素，对储罐的抗风性能进行了数值模拟[3-7]。由文献[8-13]可知，通过风洞试验和数值模拟，可以分析风压的分布情况；脉动风速谱、雷诺数、风向对储罐存在干扰效应。由文献[14-15]可知，抗风元件也影响储罐的抗风能力；储罐在平均风和脉动风的作用下会产生不同形式的响应，而响应的形式与所施加的风函数有关。储罐的高径比、材料类型也影响临界载荷。然而，对储罐的研究目前停留在初级阶段，对储罐在风载荷作用下的变形进行的研究不够全面。

通过Workbench有限元软件可以计算设备的应力[16]，本文应用Workbench软件，对静态风荷载作用下的储罐进行了屈曲分析。通过有限元模拟计算，得到了储罐的临界风压和变形图，研究了储罐的位移与周向角的关系，比较了不同高度处的应力情况；通过改变风速，研究了罐壁迎风面和背风面的响应状态，以期对以后的工程实践提供理论基础。

1 储罐屈曲分析理论基础

1.1 风载荷的计算

风载荷是由空气流动产生的，可用风速表示风载荷。风载荷的作用受设备高度、设备所处环境、设备的外形等各种因素的影响。《建筑结构荷载规范》[17]给出了风载荷标准值的计算式：

式中，λ为驻点（周向角为0°的罐壁最高点）的风压幅值，Pa；βz为建筑物在高度z处的风振系数；μs为风荷载体型系数；μz为风压随高度z的变化系数；ω0为风载荷，Pa。为了便于计算，工程上通常把风速换算为风载荷。根据伯努利方程[18]，在标准大气压、温度为15℃的条件下，风速与风载荷的关系可表示为：

式中，ν0为风速，m/s。根据风速的大小，风力可分为不同的等级，风速越大，风载荷越大，风的作用越强，储罐的结构越易发生变形和失效。

1.2 储罐风压分布

风压在罐壁周围的分布不均匀，空气流动对储罐的结构产生动压力。由于风压沿高度的变化很小，一般可以忽略，因此本文认为风压在罐壁竖直方向上分布是均匀的[19]。对于风压的周向分布，国内外给出的形式各不相同。我国标准GB 50009—2012《建筑结构载荷规范》所给出的风压体型系数是一系列不连续的数，而国外的众多学者通过采用三角函数分析风洞试验的方法，得到了风压分布公式。目前，数值模拟大多采用R.F.Rish[20]研究所得的周向函数，本文拟采用此周向函数：

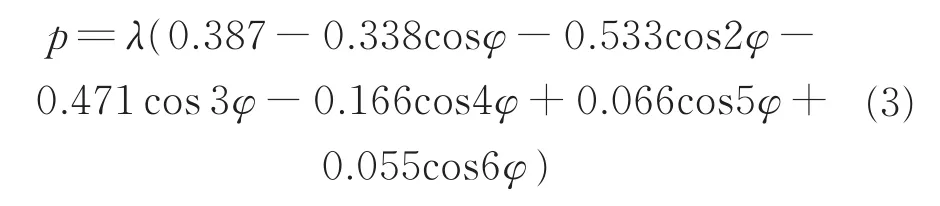
式中，p为施加在储罐罐壁外侧的风载荷，Pa；φ为储罐沿圆周方向的展开角，（°）。除了储罐罐壁外侧的风载荷，储罐罐壁内侧存在负压，驻点内侧的负压最大，其值为储罐外壁驻点处风载荷的1/2[21]。

1.3 特征值屈曲理论

当储罐所受载荷和结构保持平衡时，储罐处于稳定状态；当储罐所承受的载荷达到某一值后，其结构发生变化或者达到另一种平衡状态，去掉干扰后结构仍然保持变形状态，不能恢复到原来的结构，此时储罐处于失稳状态，又称屈曲状态，外力的极限值被称为临界载荷。线性屈曲分析以特征值为研究对象，可得到线弹性结构的极限载荷，计算所需时间短，可用于预测结构的屈曲形状。线性屈曲分析需要对式（4）求解：

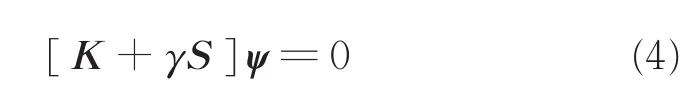
式中，K为结构总体刚度矩阵；S为应力硬化矩阵；ψ为屈曲模态位移矩阵；γ为特征值。进行分析时，先进行静力学分析，施加载荷和约束，用于计算应力硬化矩阵S。然后，采用屈曲模态分析的方法，设定储罐变形结果和模态数，得到临界载荷因子即特征值γ。施加的载荷乘以临界载荷因子，即可得临界载荷。

2 储罐有限元模型建立

2.1 储罐的参数

选取5万m3立式浮顶储罐（储罐，下同）作为研究对象，分析其在风力作用下发生的屈曲情况。储罐内径D=60.0 m，罐壁总高H=19.2 m，罐壁由8层不等壁厚的壁板组成，壁板厚度由下至上依次减小，储罐罐壁的高度见表1。表中，i表示壁板所在层（从上到下）。

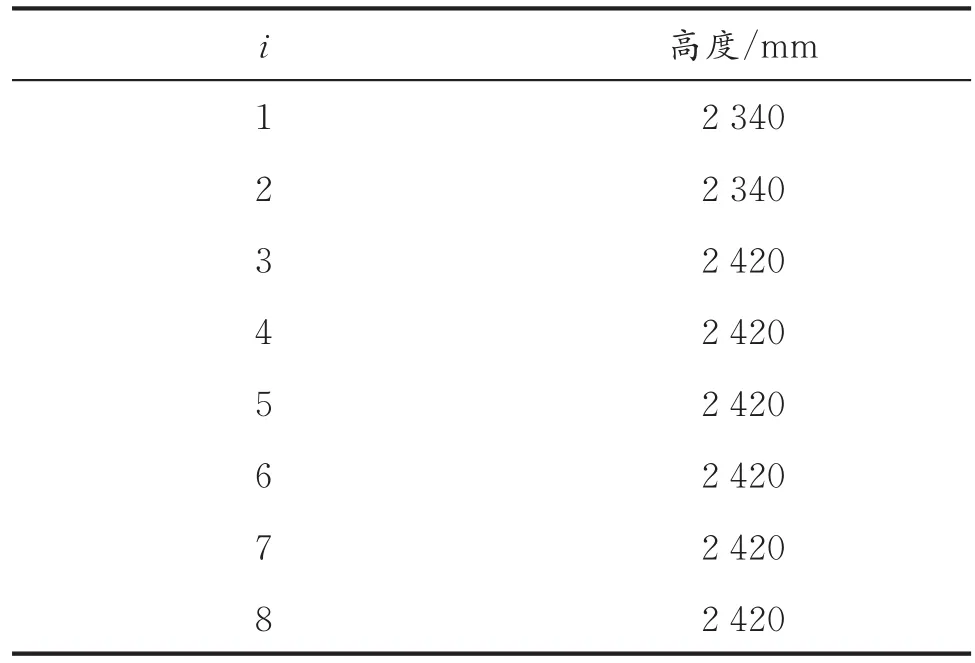
表1 储罐罐壁的高度

罐壁材料选取Q345R，其性能参数见表2。

表2 罐壁材料Q345R性能参数

2.2 边界条件及假设

储罐在不盛装液体的情况下容易发生风力屈曲，因此以空罐为研究对象，不考虑包边角钢、抗风圈、加强圈及其他附件的影响。储罐罐壁底部采用锚固的方式，约束罐底的全部自由度，在储罐的外侧表面施加风力载荷，风压以面载荷的形式施加，驻点处风压幅值取500 Pa。

2.3 储罐的有限元模型

对储罐建模，外浮顶储罐是敞口的，不再另设顶盖。由于约束储罐底部全部自由度，其效果等同于罐底固定，因此在建模时省去了罐底。为几何体分配材料，对模型进行网格划分。网格划分的储罐网格模型如图1所示。

图1 网格划分的储罐网格模型

3 模拟结果与分析

3.1 储罐风力屈曲分析

通过特征值屈曲分析可以得到储罐屈曲变形的临界风压和失效情况，将设定的条件施加于有限元模型，软件可读取设定模态的结果。本文在模拟过程中设定了储罐的4阶模态，不同阶数下储罐的屈曲模态如图2所示。

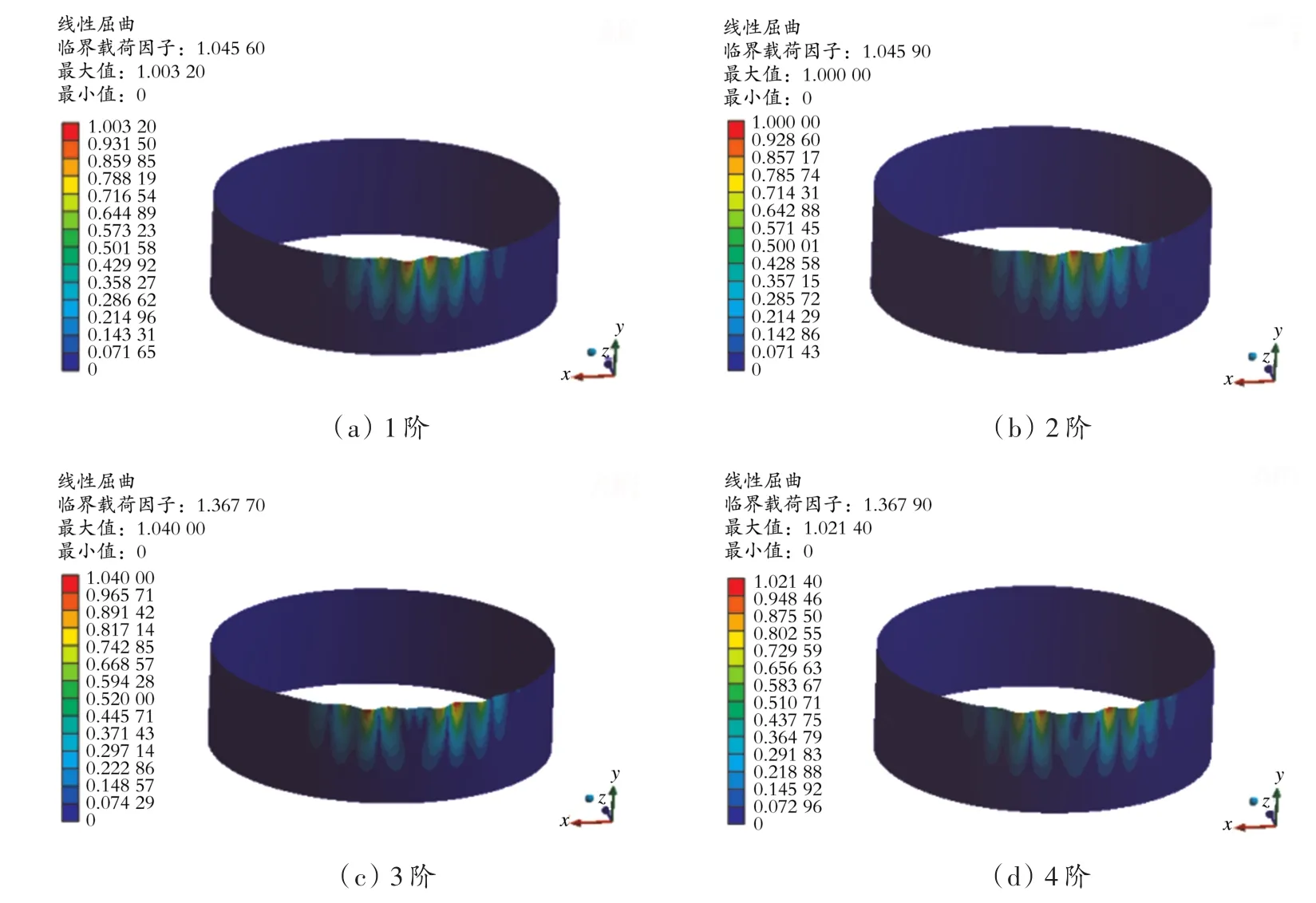
图2 不同阶数下储罐的屈曲模态

由图2可以看出，储罐的前4阶屈曲载荷因子分别为 1.045 60、1.045 90、1.367 70、1.367 90。第 1阶临界载荷因子最小，通常以此值为基础计算临界失稳值。当风力达到失稳的1阶模态时，储罐会发生屈曲失效现象。经计算可知，储罐的临界风速为26.49 m/s。查阅风速表[22]可知，此风速属于十级狂风，因此需要对储罐加强防护。储罐的临界屈曲载荷因子随着阶数的增加逐渐增大，储罐的屈曲变形程度也逐渐变大。储罐的屈曲变形以周向角0°处为中心向两侧扩展，一般情况下屈曲变形发生在罐壁上部，罐顶的变形最大，罐壁下部壁板变形不明显，这是因为罐顶壁板最薄，且没有包边角钢等加强原件的约束。因此，设计时应施加一些抗风件，以保证储罐的安全应用。对于有顶盖的储罐，其屈曲变形有待于进一步研究。

3.2 储罐静力响应分析

为了更直观地描述储罐的变形情况，绘制了储罐最上端壁板周向角与位移的关系曲线，结果如图3所示。由图3可知，储罐壳体位移以径向位移为主，周向位移和轴向位移变化不明显，径向位移变化主要发生在罐体迎风面和侧风面。在周向角约20°处，储罐受到的风力作用最强，此处产生的径向压缩位移最大，为0.667 mm；随着周向角的增加，径向位移由负值逐渐变为正值，这是由于风对罐壁的作用由压力变成吸力，产生了拉伸位移，径向膨胀位移在周向角约60°处最大，其值为1.040 mm；在储罐的背风区域中，由于罐壁所受风力较小，所产生的径向位移较小。

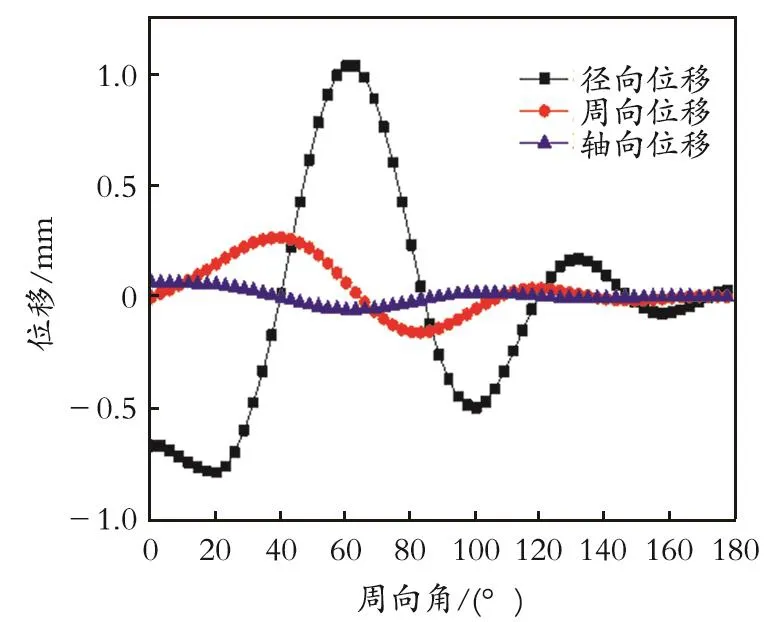
图3 储罐最上端壁板的位移与周向角的关系曲线

为了更好地分析罐壁在不同高度处的应力，绘制了储罐罐底及储罐外壁高度为10 m处罐壁的应力分布曲线，结果如图4所示。

由图4（a）可以看出，在高度为10 m处，风载荷对储罐产生的应力以周向应力为主，在周向角为0°处周向压应力最大，其值为1.510 MPa；在周向角为0°～60°时，随着周向角的增大，压应力逐渐减小，在周向角约40°处压应力降低为0，周向角大于40°时，壁面受到拉应力的作用，且呈逐渐增大趋势，周向角为60°时拉应力达到最大，其值为0.688 MPa；周向角大于60°时，罐壁受到的拉应力逐渐减小，周向角大于130°时拉应力变化不大，周向应力和轴向应力的值比较接近，这是由于风载荷对背风面的影响不大。

由图4（b）可以看出，在储罐底部，由于全部的自由度均被约束，风载荷引起的应力以轴向应力为主，波动明显，周向应力的作用不大，变化比较平稳；在周向角小于40°时罐壁受到风载荷表现为轴向压应力，且随着周向角的增大逐渐减小，周向角为0°时轴向压应力最大，其值为1.240 MPa；周向角为40°～60°时，轴向拉应力逐渐增大，周向角约为60°时拉应力最大，其值为1.500 MPa。这说明相同的风载荷对储罐不同部位的影响不同。

3.3 不同风速下罐壁应力分析

Mises应力又称等效应力，可以用来评价材料的屈服强度。以周向角0°和180°的罐壁处为研究对象，施加15、20 m/s和25 m/s的风速，进一步研究了不同风速下储罐迎风面和背风面上等效应力的分布情况，结果如图5所示。

由图 5（a）可以看出，在周向角为 0°处，风速越大，等效应力越大，变化趋势越明显；罐壁高度为0～2.5 m时，等效应力波动较大；在罐壁高度为0.9 m处，等效应力出现了第一个极小值；罐壁高度大于0.9 m时，等效应力随着罐壁高度的增加总体表现出上升的趋势。在罐壁高度为2.5 m处，等效应力出现极大值，之后等效应力随罐壁高度的增加而增大；风载荷越强，等效应力随罐壁高度增大的速度越快，这说明风速会影响储罐的受力。

由图5（b）可以看出，随着罐壁高度的增加，最大应力呈现出先减小后增大的趋势，风速越大，风载荷对罐壁的作用越强，等效应力的增幅越大，等效应力在罐壁高度为6.4 m处出现了最小值，等效应力减小的速度没有增加的速度快，罐顶处的等效应力不是最大，在接近罐顶处等效应力值达到最大，背风面的等效应力小于迎风面，不同高度处的风载荷对罐壁的影响不同。

4 结 论

（1）储罐的屈曲变形发生在罐顶处，位移以径向位移为主，设计时应考虑加强圈、包边角钢的作用。

（2）风载荷对罐壁不同位置的作用不同：当周向角为0°～40°时，罐壁受到风的压应力影响，壁面向内凹陷；当周向角大于40°时，罐壁受到拉应力的作用，当周向角为60°～120°时拉应力变化明显，壁面向外侧突出；罐底所受力以轴向应力为主，随着罐壁高度的增加，风载荷的作用转变为以周向应力为主。

（3）风速越大，罐壁变形程度越大，背风面罐壁的受力小于迎风面。随着风速的增加，周向角为0°处等效应力呈上升趋势，但是在靠近罐底处出现波动，而周向角为180°处呈现先减小后增大的趋势。