基于集合分划的数列收敛的等价条件*

黄思思，桂绍辉

(赣南师范大学 数学与计算机科学学院，江西 赣州 341000)

为讨论问题的方便，先给出下面2个定义.

定义1[1]设A为一个非空集合，Ω={Ai|i∈I}表示集合A的某些非空子集所构成的集合，如果集合A的每一个元素在且只在其中某一个Ai中即Ai∩Aj=Ø,当i≠j时，则称集合Ω是集合的一个分划，且若|Ω|=k时，则称这种分划是分k类的分划.

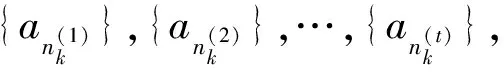
关于用子列判断数列收敛问题，在文献[1]中，对文献[2]中的结论“数列{an}收敛⟺{a2k-1}和{a2k}收敛且二者极限相等”作了进一步推广，得到以下结论：

引理[1]数列{an}收敛⟺{an}的任意分数列{an}为t类的子数列均收敛，且它们的极限相等.

本文在此结论基础上进一步分析得到如下定理：

……,

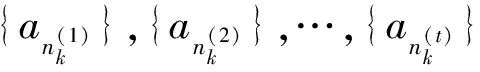
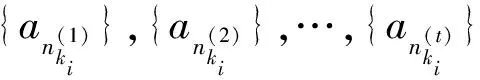
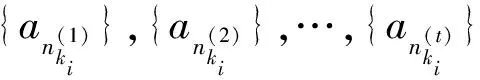
即有

由引理[1]可得数列{an}收敛.

反之,利用数列与子列的关系易得.

例1若数列{a2k-1}、{a2k}和{a3k}收敛，能否保证数列{an}收敛？

证明数列{an}是收敛的.事实上，

基于此可进一步得到以下2个推论：

推论1已知数列{a2k-1}、{a2k}收敛，若数列{an}的另一子列{aq·k}收敛(其中q=2l+1,l∈N)，则数列{an}收敛.

推论2已知数列{atk}，{atk-1}，{atk-2}，…，{atk-(t-1)}收敛(其中t∈N+，且t≥3)，若数列{an}的另一子数列{aq·k}(其中q=tl+1,l∈N)收敛，则数列{an}收敛.