行星齿轮传动系统内齿圈振动特性分析

林祖胜，张绍辉

（1.厦门理工学院机械与汽车工程学院，福建 厦门 361024；2.福建省客车及特种车辆研发协同创新中心，福建 厦门 361024）

1 引言

行星齿轮传动具有结构紧凑、输出功率大和传动平稳等特点，目前已被广泛运用于风力发电设备、大型矿山机械和航空航天等机械传动领域。受结构复杂及负载超额等影响，行星齿轮传动系统失效率较高，据国外企业统计，行星齿轮系统故障约占风电增速箱故障的54%左右[1]。

作为行星齿轮传动的关键部件，内齿圈在工作过程中柔性较大且受力复杂，设备监测与故障诊断时传感器通常固定在齿圈部位，其它零件的信号通过不同传递路径到达齿圈位置，因此分析内齿圈的动态性能对于改善行星齿轮系统的振动和噪声具有重要意义。文献[2]通过建立计入齿圈柔性的直齿行星传动精细化动力学模型，获得低阶固有频率及振型，揭示了齿圈柔性对传动系统动态性能的影响；文献[3]结合Hertz接触理论和齿轮激励，建立考虑齿面接触特性的动力学模型，探究内齿圈断齿故障下系统的动态特性；文献[4]对行星齿轮传动系统进行三维实体建模和动力学仿真分析，得到不同工况的动力学特性仿真结果并分析振动特点及原因；文献[5]根据结构及边界特点采用平面梁单元建立行星齿轮柔性内齿圈的振动分析模型并进行固有特性研究，获得三类弹性边界振型。通过建立精确的模态仿真模型，运用有限元法对某风力发电机用行星齿轮箱内齿圈进行分析，有效地指导相应的试验模态过程，简化试验步骤，避免传感器安装、部件固定等错误，验证了内齿圈模态模型的有效性。

2 模态分析基本理论

模态分析主要通过理论计算或试验方法获得模态参数，为结构动态特性分析优化、振动监测与故障诊断等提供依据。根据弹性力学有限元法，齿圈的运动微分方程为：

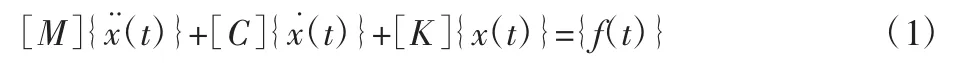
式中：［M］—质量矩阵；［C］—阻尼矩阵；［K］—刚度矩阵；｛x¨（t）｝—振动加速度向量；｛x˙（t）｝—速度向量；｛x（t）｝—位移向量；｛f（t）｝—系统所受外界激振力向量。

研究齿圈自由状态下模态特性，外力｛f（t）｝=｛0｝且忽略阻尼对自由振动固有频率和振型的影响，式（1）简化为：

相应的特征方程为：

式中：λi—特征值，系统的固有频率；｛φi｝—特征向量，系统的模态振型。由瑞利法可知第i阶固有频率和振型有如下关系：

假设振型已完成模态质量归一化处理，模态质量有：

则第i阶模态频率对第Sj个设计参数的灵敏度为[6]：

由于模态分析实际上是振动方程的解耦过程，由式（6）可知，结构参数的变化直接影响质量矩阵和刚度矩阵，从而改变固有频率。在系统模型结构确定的情况下，模态质量与结构材料密度有关，模态刚度与结构参数的弹性模量和泊松比有关，因此有限元模态分析必须定义材料的密度、弹性模量和泊松比等参数。

试验模态分析主要基于外部激励力和系统结构的动态响应，利用试验设备采集测点的响应数据，经过信号处理完成模态参数识别。通过对式（1）进行傅里叶变换得到：

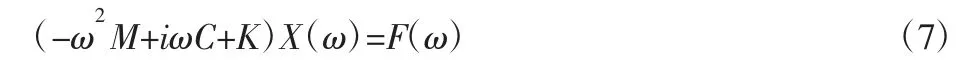
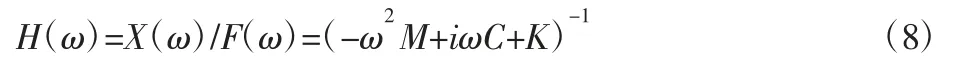
频率响应函数矩阵H（ω）可表示为：理论上只需测量频响函数矩阵的行或列即可识别各阶模态参数，两者之间的关系为：

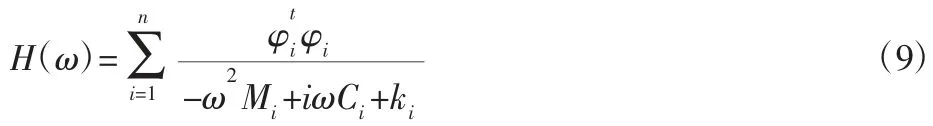
式中：mi—模态质量；ci—模态阻尼；ki—模态刚度；φi—振型向量。

3 齿圈模态分析

3.1 齿圈有限元模态分析

齿圈的基本设计参数，如表1所示。

表1 齿圈的基本设计参数（mm）Tab.1 Design Parameters of Ring Gear（mm）

利用SolidWorks软件GearTrax模块建立三维参数化模型，以Iges格式导入Hypermesh软件进行有限元模态分析，主要步骤如下：（1）几何清理：模型导入与几何清理是建立高质量网格的关键，通过autocleanup等面板，删除或重建错误的连接关系，由于齿圈结构较为规则，避免因极大的简化而造成的误差；（2）材料42CrMo，各向同性，弹性模量206GPa，密度7.85g/cm3，泊松比0.28；（3）网格划分：选择三维Hex8单元，经试算控制单元大小1.5mm，根据结构循环对称特点，最小旋转角度为45°，切分出模型1/8部分，在2D网格的基础上利用spin、solidmap等工具将齿圈离散为全六面体网格，在尽量小的计算规模下获得尽可能精确的仿真模型；（4）质量检查：通过QualityIndex、CheckElems等模块进行单元优化调整，控制单元的翘曲角、雅可比、扭曲度和长宽比等指标，最终获得381387个六面体单元及87055个节点，如图1所示。模态特性是系统在自由振动状态下的固有特性，为了尽量消除不必要的干扰和影响，便于有限元模态与试验模态对比，设定两种分析均处于自由边界状态即不施加任何载荷和约束等。在Hypermesh软件中通过添加EIGRL卡片设置频率求解阶数或范围，选用Radioss求解器进行齿圈有限元自由模态分析，将分析结果导到Hyperview软件处理。

图1 Hypermesh环境下齿圈有限元模型Fig.1 Finite Element Model of Gear Ring

由于低阶模态对结构振动贡献更大，基本决定结构的动态特性，同时被测齿圈为对称结构，导致有限元模态求解时出现重根现象，部分阶次的固有频率数值非常接近，仅存在相位差别，因此去除相近频率和刚体移动模态（频率值接近0Hz），经整理取前8阶固有频率和振型，如表2所示。为了描述方便，根据振型表现将齿圈的低阶模态振型分为：弯曲振主要呈现齿圈端面的弯曲振动，径向振主要呈现齿圈沿径向伸缩振动，扭转振主要呈现轴向基本无振动、各端面相对扭转振动，伞型振主要呈现轴向振动伸缩成呼吸状或伞状，对折振主要呈现轴向波浪振型。

表2 计算模态频率与振型描述Tab.2 Natural Frequency and Modal Shape Description

3.2 齿圈试验模态分析

为了验证模态仿真模型的准确性，采用力锤单点激励多点响应的频响函数法对行星齿轮齿圈进行无预紧力自由试验模态分析，试验系统由激振系统、数据采集系统和模态分析系统等组成，如图2所示。力传感器和三向加速度传感器分别拾取激励力信号和各测点响应信号，通过同轴电缆，经放大器后传输到LMS SCADAS数采前端进行数据初步处理，然后通过网线传送到计算机LMSTest.Lab模态分析软件进行参数识别，试验系统规格及性能参数，如表3所示。

图2 模态试验系统方案Fig.2 Design of Modal Experiment Analysis

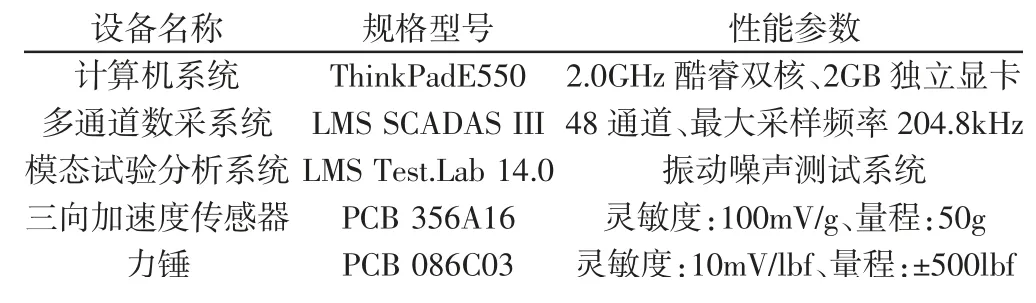
表3 试验系统规格及性能参数Tab.3 Specifications of Modal Test System

基于有限元模态振幅较大位置等结果，为试验模态中悬挂方式、激励点和测点布置等提供指导，主要步骤如下：

（1）试验前的准备即建立测试系统，包括悬挂工件、安装传感器、线缆连接各部件、建立几何模型等，试验现场为了模拟自由边界条件和隔离环境或基础振动对模态提取的影响，将被测齿圈用弹性吊带自由悬挂，所用弹性吊带的伸缩频率应低于齿圈最低频率的十分之一，如图3（a）所示。结合仿真模态中振幅较大位置，经过单点多次试测，寻找最佳激励点。合理的测点位置和数量对试验模态分析精度至关重要[7]，根据有限元模态振型和齿圈结构特点，加速度传感器的布置应避开各阶模态振型的节点，提高信噪比，在模态分析软件中建立齿圈的几何试验模型，如图3（b）所示。总共布置32个测点（a1-a16，b1-b16），均布在仿真模型变形量较大部位或振动峰值处等位置；

（2）试验过程，通过连续采样方式，设置带宽即最高分析频率为8192Hz，频率分辨率0.5Hz，移动力锤选取合适的敲击方向分别激励每个测点5次，保证力锤信号无连击与过载，实时检查各测点的相干函数值，对激励力信号和响应信号分别加力窗和指数窗以防止能量泄露；

（3）数据处理即模态参数识别，将各测点采集的数据导入LMSPolyMAX模块，经带宽设置、极点选择及振型计算等步骤，获得模态稳态图，如图4所示。模态定阶时应选取纵向S值（模态稳态图的最优极点）较多的波峰位置。

图3 试验现场图片及测试模型Fig.3 Test Scene Picture and Test Model

图4 PolyMAX识别的稳态图Fig.4 Stabilization Chart of Poly MAX Recognition

3.3 模态分析结果对比

由于试验模态存在各种因素影响如仪器误差、环境噪声等，导致部分频率遗漏丢失或振型无法计算（对应有限元模态第2阶、第7阶），但是试验模态是反应结构在真实环境下的动态特性，其结果仍比有限元仿真更可靠，因此基于试验模态分析结果，去除有限元模态第2、7阶后经重新整理，如表4所示。可见有限元模态和试验模态固有频率相关性较好，多阶频率保持一致，最大相对偏差仅为3.02%，其中有限元模态计算结果略偏大，这主要由于有限元仿真基于对连续几何体的离散，造成结构刚度变大，若能进一步细化单元和节点，仿真结果将更加趋向试验值，同时对应阶次的仿真模态与试验模态的振型吻合较好，如图5所示。模态振型描述基本一致，如表2所示。

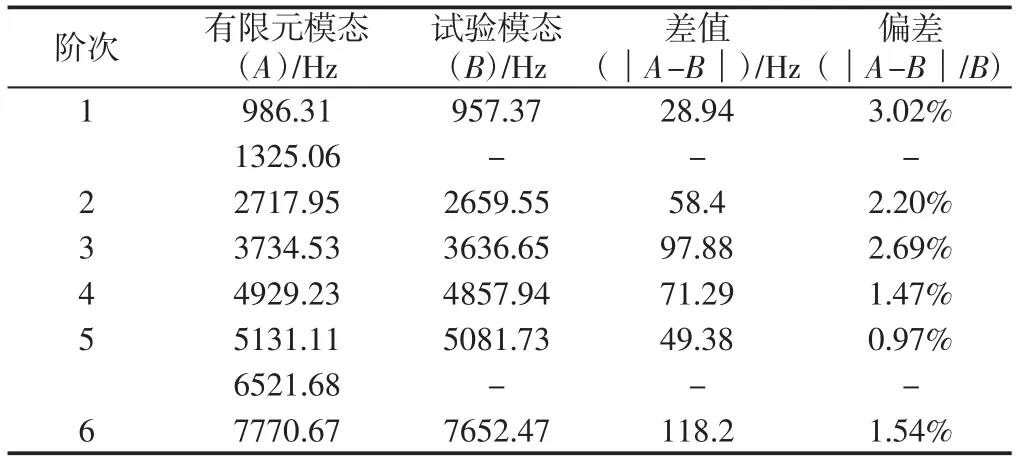
表4 有限元与试验模态频率对比Tab.4 Frequency Com parison of FE Analysis&Modal Test

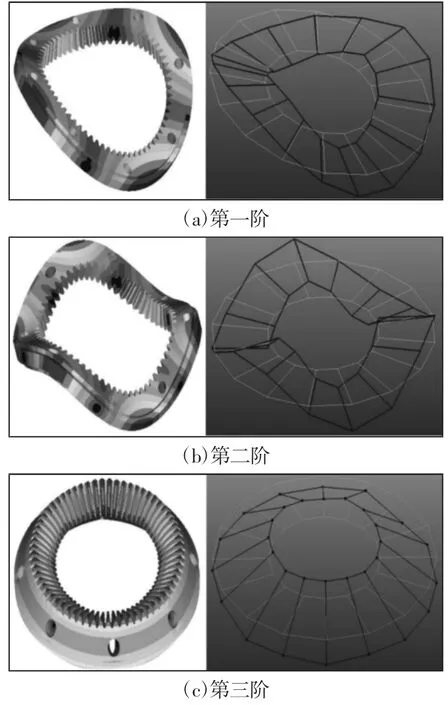
图5 仿真模态与试验模态振型对比Fig.5 Comparison of Simulation Mode and Experimental Mode

通过试验模态和有限元模态的结果对比，相关性较好，证明所建立的行星齿轮内齿圈全六面体网格模态模型能较好地反映结构振动的实际性能，可以作为保证后续动态特性准确可靠分析的基准模型。

4 齿圈动态特性仿真

4.1 齿圈柔性对固有特性的影响

内齿圈的柔性对抑制行星齿轮系统的振动和降低传动噪声具有重要影响，有利于提高行星齿轮系统的功重比。由于内齿圈的柔性与内齿圈的厚度之间息息相关[8-9]，为了直观分析统计，以厚度来表征内齿圈的结构柔性，通过分析内齿圈厚度和固有频率之间的关系，考察内齿圈柔性对系统固有特性的影响。

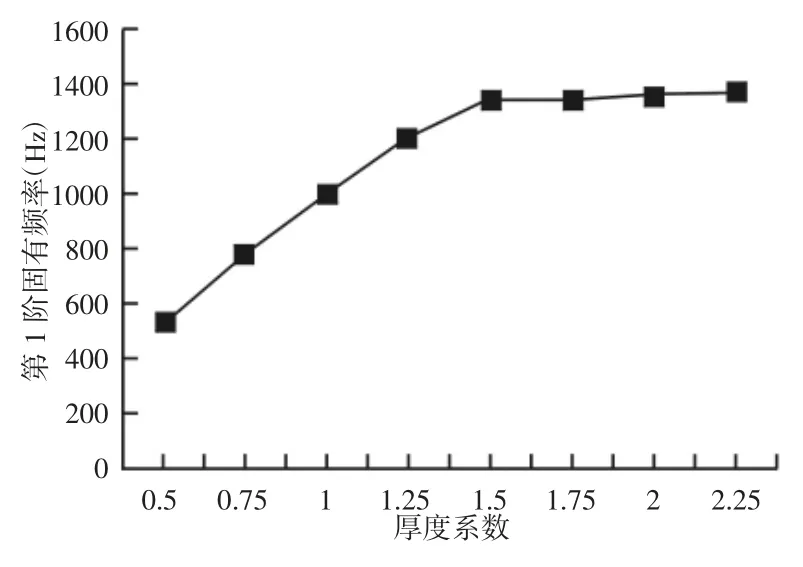
图6 内齿圈厚度对系统第1阶固有频率的影响Fig.6 Effect of Thickness on Natural Frequency（N=1）

以表1参数为基准值，在其他设计参数不变的条件下，利用上述所建模态仿真模型，借助Hypermesh软件功能，对齿圈厚度方向单元进行“scale”、“remesh”、“smooth”等操作，按比例直接改变齿圈厚度并进行有限元自由模态分析。经过反复试算后发现，随着内齿圈厚度的增加，齿圈的结构刚度增大，系统的第1阶固有频率也随之增大，因篇幅所限仅给出齿圈厚度系数在［0.5，2.25］即厚度为［12mm，54mm］变化范围，如图6所示。表明齿圈的柔性越大，系统的固有频率越高，但在一定厚度范围后，固有频率变化趋于平稳，内齿圈的柔性可作为行星齿轮分析的一个重要影响因素。

4.2 典型断齿故障的工作模态仿真

由于行星齿轮系统部件故障状态下的动态特性对其故障的监测与诊断具有重要意义，在Hypermesh软件中通过“delete-elems”命令直接对上述齿圈模态仿真基准模型删除一个齿的全部单元，模拟单条轮齿断裂故障，进行典型断齿故障下的内齿圈实际工作模态分析。

虽然在实际工作中存在各种约束，但对于齿圈的模态分析，相对于本身的结构和刚度，约束的位置和大小对其固有频率的影响较小[10]，因此在齿圈螺栓孔内表面施加各个方向的自由度约束，无需施加力载荷等其他边界条件。从有限元仿真结果发现，单条轮齿断齿故障情况下齿圈的工作模态频率为11791Hz，该模态频率下为扭转振动，如图7所示。

图7 典型断齿故障齿圈模型及工作模态Fig.7 Establishment and Working Mode of Ring Gear with Broken Tooth

5 结论

（1）通过有限元模态与试验模态的对比分析，识别了内齿圈结构的模态参数，低阶固有频率的最大相对误差仅为3.02%，对应振型吻合较好，验证了所构建的全六面体内齿圈模态仿真模型的合理性和计算精度；（2）基于模态模型，以齿圈厚度表征系统的结构柔性，随着厚度增加，结构刚度增大，第1阶弯曲振动频率显著增大，齿圈的结构柔性对其振动特性有着至关重要的影响，同时获得单条轮齿断裂典型故障下的齿圈工作模态频率及振型。