伸缩臂式起重机阶梯柱模型的临界力计算对比

姚峰林，孟文俊，赵 婕，石国善

（1.太原科技大学机械工程学院，山西 太原 030024；2.太原大学计算机工程系，山西 太原 030032）

1 引言

随着建筑物的高度不断增加和风力发电、石油化工、核电工程、矿业冶金等行业的快速发展，使得大型工程起重机的市场需求量越来越大。特别是高强度钢材在伸缩臂架上的应用和单缸插销技术使全地面起重机获得重大进步，最具代表性的如某国Liebherr LTM 11200，徐工集团QAY1200，三一重工的SAC12000，中联重科的QAY2000等，这些全地面起重机的伸缩臂架的阶数都达到了8阶，起升高度大，起重量大，转场效率较其它类型的起重机得到显著的提升。随着起升高度、起升重量的不断增加，伸缩臂的截面积也相对增大，在加工和制造工艺允许的范围内，合理地利用材料和减轻重量就变得越来越重要。

阶梯柱模型是此类伸缩臂架的受力模型，然而伸缩臂架的稳定性是决定起重机起质量和安全关键，所以阶梯柱模型的稳定性也就成为了学者研究的重点。Timoshenko等对阶梯柱模型进行了较为深入的研究和分析，并使用能量法给出了二阶阶梯柱的临界力的结果，并且给出了其他一些近似的计算方法，这些方法在阶梯柱的阶数不高时，都可以得到较高的精度[1]。国内也有学者借助预设近似挠度曲线，使用能量法和李兹法对阶梯柱进行研究，但这种方法相当于引入附加约束，对于三阶以上的阶梯柱就会产生比较大的误差[2]。文献[3]使用传递矩阵法对阶梯柱的临界力进行了研究，但这类方法目前也只能用于阶数较少的阶梯柱，在阶数较高的阶梯柱使用该方法也会出现较大的误差。随着有限元理论的发展和完善[4]，文献[5-6]使用精确有限元法对阶梯柱的临界力进行了研究。

我国现行的国家标准采用了精确有限元法作为规范的阶梯柱稳定性分析方法，但这种方法对于多阶阶梯柱来说，其刚度矩阵相当庞大，特征方程复杂，对于常见支撑形式的阶梯柱稳定性精确数值解常通过试凑法获得，计算量巨大，给实际应用带来了一定的困难[7]。在现行的设计规范中使用了图表来表示（2～5）阶的阶梯柱的部分特殊组合情况下的长度系数[8]。当阶数超过5阶时，设计规范就无法应用；并且在非特定组合时使用线性拟合的方法，却没有给出线性拟合的误差。这时规范的使用就无法满足实际工程的需要，因而急需一种方法，可以较方便且迅速地求解5阶及以上阶梯柱临界力的方法，并且对于各种非特殊组合也可以给出高精度的解。

2 能量法

2.1 理想柱的挠曲线

对于形状简单的柱状承载构件，其受压，如图1所示。对于压杆的临界载荷，是由压力与弯曲力共同作用或由初弯曲得到的。对于前一情形，临界荷重由轴向载荷值所决定，就是即使横向荷重很小，轴向力将引起很大的横向挠度。同样地，对于具有很小的初弯曲的杆，当压力趋近于临界值时，挠度将无限地增大。

图1 理想柱的挠曲Fig.1 Deflection of Ideal Column

如图所示理想柱的挠曲微分方程为：

记；

代入理想柱端点条件，并取适合方程的最小kl值，即满足以使杆保持微小弯曲的最小轴向力，可得挠曲线方程为：

2.2 瑞利-李兹法求解理想柱欧拉临界力

根据势能驻值原理，在满足平衡条件真实的位移使结构的势能为驻值，即结构势能的一阶变分为零，使用能量法可以确定临界荷载。不论柱的变形是大挠度变形还是小挠度变形，此临界载荷都可以使用此法时行求解。这里使用（3）式作为理想柱失稳后的挠曲线。

理想柱的弯曲应变能为：

外力势能为V，这里使用如图1所示的d s的近似：

由驻值原理EP=ΔU+V和可得；

2.3 用理想柱挠曲线求解阶梯柱的长度系数

图2 变截面阶梯柱模型及受力简图Fig.2 Mechanical Model and Force Diagram of Multi-Stepped Column

等截面柱并不是最经济的承载结构形式。在起重机伸缩臂架中，截面常常是突然改变的，伸缩臂截面通常用钢板模压和焊接组成，因而阶梯柱状是伸缩臂目前最合理的结构。要求解阶梯柱的临界力值，就必须对于柱的每一段分别列出挠度曲线的微分方程。

针对n阶阶梯柱模型，基于纵横弯曲理论可建立各节伸缩臂挠曲微分方程[9]。n阶阶梯柱的总长长为ln=l，从阶梯柱的根部到第i阶阶梯柱的顶端的长度为li，第i阶阶梯柱的惯性矩为Ii，如图2所示。P为伸缩臂顶端承受的轴力，且P的方向保持不变，δ为伸缩臂顶端的侧向位移，假设轴力和弯矩全部由伸缩臂承受。

假设挠曲线近似仍为式（3）中的挠曲线，（这里l=L），把式（1）、式（3）代入弯曲应变能中，得：

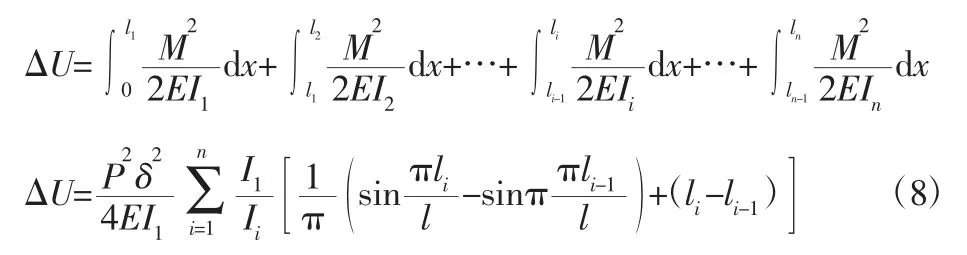
注：式（8）中，l0=0，如果外力势能继续使用式（5），由势能驻值原理可得；注：l0=0

相对于单端约束的柱来说，可以把柱的截面的变化以长度系数μ2来进行考虑；

阶梯柱的长度系数μ2就为：

2.4 假设挠曲线为抛物线求解阶梯柱的长度系数

通过假设阶梯柱变形曲线，利用能量法计算阶梯柱的屈曲临界力，考虑到二次曲线与余弦函数的接近性，有学者提出使用抛物线来假设挠曲线。

弯曲应变能为：

3 数值解析法

3.1 n阶阶梯柱的递推公式

考虑到能量法使用了假设曲线来近似阶梯柱的挠曲线，所以其相当于在阶梯柱上施加了人为约束，所以误差是无法避免的。另外，能量法在计算势能的时候也使用了曲线微分的二阶近似，因此也会出现高阶误差，所以在精确计算时能量法就可能产生较大误差。

针对n阶阶梯柱模型，基于纵横弯曲理论可建立各节伸缩臂挠曲微分方程。n阶阶梯柱的总长为ln，P为伸缩臂顶端承受的轴力且P的方向保持不变，δ为伸缩臂顶端的侧向位移，假设轴力和弯矩全部由伸缩臂承受，第阶压杆模型的受力和变形，如图2所示。

式（16）可统一表示为

式中：

当n=1时，可以得到：

当n=2时，可以得到：

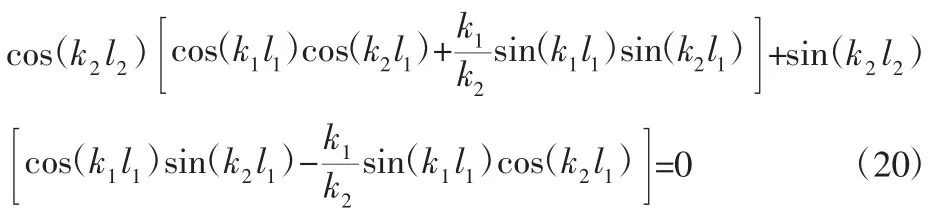
当n=3时，可以得到：

根据数学归纳法，可以证明，n阶阶梯柱的失稳特征方程如下：

此方程为超越方程，没有解析解，式中；

3.2 超越方程的数值求解

当阶梯柱的阶数为n时，超越方程组可以通过增加其约束限制限制方程建立方程组才有可能求解。

所建立的n阶超越方程组，如式（27）所示。到目前为止，这种非线性超越方程还不存在解析解，只有数值解。数值解常使用的方法包括欧拉法，龙格库塔法，Gauss-Newton等；但这些方法可能由于矩阵的奇异而无解。这里使用Levenberg-Marquardt算法[10]，这种算法同时具有梯度法和牛顿法的优点并较原来的梯度下降法提高速度几十甚至上百倍，并且对于（27）所构建的方程组总能得到最优数值解。

通过式（27）可以求解出每节阶梯柱的刚度，进而可以求出整个阶梯柱模型的临界力P，此临界力与相同约束条件下，与阶梯柱长度相等的基本臂截面所构成均等截面柱的临界力对比，就可以求出n阶阶梯柱的长度系数μ2。

图3 采用不同方法计算二阶阶梯柱的长度系数值Fig.3 Length Coefficient of Two Stepped Column Use Different Method

3.3 二阶阶梯柱的非线性及其插值

由图3可以看出，对于二阶阶梯柱其长度系数值μ2，使用理想柱挠曲线的能量法和数值法与使用ANSYS17.0所计算出的差值非常接近。其中数值法与ANSYS结果最为接近，最大相对误差为1.7×10-4，可以看出n阶压杆稳定性计算的递推公式的精度是比较高的。但使用抛物线作为挠曲线的近似曲线的能量法所计算出的长度系数μ2随着β1的增大与其它三种方法的误差变小，但在β1较小时长度系数μ2的误差比较大。因此在这四种方法中，使用抛物线作为挠曲线的近似曲线产生的误差最大。此外，随着第二阶柱（I2）的惯性矩的增大相当于是基础臂的惯性矩的增加，长度系数μ2减小，即阶梯柱的临界力逐渐增大；随着第一阶臂架（I1）长度与全臂架长度之比（α1增加），即第二阶柱的相对长度的减小，长度系数μ2非线性减小。

因此对于使用GB3811-2008时[11]，当选用了表中没有的β1时，使用比较接近的数值进行线性插值才可以得到更为准确的结果，但目前国家标准中推荐使用的是线性法，但实际上在二阶阶梯柱的时候已经呈现出明显的非线性；另外第2阶臂架长度（l2）与全臂架长度（l）之比（α1）不同时，也会影响最终的长度系数值μ2，因此，即使是二阶阶梯柱，μ2的精确计算是非常必要的。

3.4 多阶阶梯柱的长度系数

为了与GB3811-2008进行对比，我们采用了与国家标准相类似的表格。表1中的数据是二阶和三阶阶梯柱的长度系数值。由表中数据可得，使用抛物线作为阶梯柱挠曲线的方法在二阶阶梯柱时产生的误差还不是很大，但使用在三阶阶梯柱将产生巨大的误差。另外，理想柱的计算方法使用在三阶阶梯柱的时候也将产生较大的误差。因此，对于n阶阶梯柱，传统的能量计算方法使用到三阶已经非常不准确了，而GB3811-2008是使用精确有限元法计算出来的，这种算法的精度是相当高的，但由于算法本身的复杂性和数值计算收敛的困难性，国家标准中只给出（2～5）阶的阶梯柱的长度系数，但随着我国起重行业的快速发展，国家标准已经远远落后于实际生产。

数据是四阶和五阶阶梯柱的长度系数值，如图5、图6所示。在这个表格中我们不再把抛物线作为阶梯柱挠曲线的方法列入对比，因为误差已经太过于巨大了。对于理想柱的计算方法在四阶、五阶阶梯柱时产生的误差也已经相当大了，最高达20%。所以传统教科书中给出的理想柱的计算方法已经不适用于四阶、五阶阶梯柱的长度系数计算。然而，使用数值法计算出的长度系数值μ2与使用ANSYS17.0所计算出的值比GB3811-2008还要接近。

图4 二、三阶阶梯柱计算长度系数及比较Fig.4 Effective Length Factor of 2 and 3 Stepped Column

图5 四阶阶梯柱计算长度系数及比较Fig.5 Effective Length Factor of 4 Stepped Column

图6 五阶阶梯柱计算长度系数及比较Fig.6 Effective Length Factor of 5 Stepped Column

另外，对于国家标准中没有给出的βi值，GB3811使用线性插值法进行长度系数的计算，其值在小区间内插线性度较高，插值误差很小，但大区间的插值和外插值还需要谨慎使用。

由于计算的复杂和困难，对于五阶及以上的阶梯柱的长度系数，八阶阶梯柱长度系数与现有文献和ANSYS17.0进行比较，发现此递推公式与Levenberg-Marquardt算法相结合所求解出的长度系数具有极高的精度，优于文献中所计算出的长度系数值，如表1所示。因此，提出的算法对于大型n阶起重机臂架压杆稳定性具有很强的实用意义。

表1 八阶阶梯柱计算长度系数及比较Tab.1 Effective Length Factor of 8 Stepped Column

4 结论

对于大型工程起重机来说，伸缩臂架作为主要的受力部件，决定着起重机的主要性能，相对于桁架式臂架其具有更强的灵活性，因而在工程起重机当中被大量使用，有关其的研究至关重要。

使用伸缩臂的阶梯柱模型，对n阶阶梯柱的稳定性微分方程组进行推导，得到n阶阶梯柱递推公式，根据阶梯柱模型的力学和结构特性，列写补充方程；使用Levenberg-Marquardt数值算法求解n阶阶梯柱的超越方程组，与现行国家标准GB3811-2008和ANSYS17.0所得结果进行对比，结果表明n阶阶梯柱递推公式正确；数值解法相比其他的计算方法通用性更强，精度更高；此外，阶梯柱模型的长度系数具有一定的非线性性，小范围内的插值不会产生太大的误差。但对于大截面的阶梯柱模型，使用插值法计算，临界力的误差较大。