一种摆腰式无膝双足机器人的机构设计及运动分析

韩 军，郑 阳

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

1 引言

近几年来科学技术不断发展，机器人相关的技术突飞猛进不断取得突破。机器人技术的发展水平渐渐成为各国之间科技水平角逐的综合评定指标之一[2]。到目前为止，双足机器人主要应用领域包括康复医学、智能假肢等人体医疗方面。由于双足机器人的结构等接近于人类身体，当在机械结构上添加足够的传感器和感应器后，它就可以替代人类从事一些复杂、繁重、危险的作业工作[3]，比如太空探险、海底勘探、核污染现场作业等，因此双足机器人的研究具有非常重要的意义。

创新设计的摆腰双足机器人，主要应用于机器人原理示教以及机器人快速竞速比赛等场合，甚至可以作为双足机器人快速运动时的一种状态。

2 摆腰双足机器人概述

2.1 机构的创新设计

以双足机器人为基础进行研究的，以提高双足机器人在直线运动的运动速度为目的。经过对各种双足机器人的调研与分析[4]，我们发现，机器人在运动过程中有相当的一部分时间是被用在寻找机体的重心，保持自身的稳定性能。因此，我们创新设计了一种无膝的摆腰双足机器人，旨在通过改变上半身的重心来保持平衡，以此减少腿部的运动及计算时间[1]。将上半身改进成可以左右摇摆的机构，创新设计了摆腰式的无膝双足机器人，与实验室原有的双足仿人机器人结构迥异[4]，需要对其结构、自由度、机构元件等进行自主设计。

2.2 工作原理

摆腰双足机器人的工作原理，如图1所示。其工作原理就是上、下半身电机协调运动，实现重心偏移，从而带动腿部机构离地，从而实现整体机构的向前运动。

图1 工作原理图Fig.1 Working Principle Diagram

当上下电机协调运动时，上半身电机带动上半身机构向左摆动时，机体重心向左偏移，右脚离地；同时，下半身电机（髋部电机）带动右腿机构向前运动；同理，当上半身机构向右摆动时，下半身电机带动左腿部机构向前运动，如此双腿交替前进，从而实现机器人整体向前的运动。

2.3 自由度选择及部分结构数据参数

根据结构原理，在摆腰双足机器人的腰部设置一个转动电机（由上半身电机带动）实现上半身的左右摆动的转动关节；在胯骨关节处设置一个转动电机（由下半身电机带动）实现腿部的前后摆动的转动关节；在左右两脚踝关节处各设置一个自由转动关节，以减少机体与地面的冲撞；在左右两手臂的肩膀处各设置一个转动关节，来保持双足机器人在前进过程中的平衡[5]。

图2 结构图Fig.2 Structure Diagram

依据摆腰双足机器人的仿真模型及所需材料特性[5]，可以得到部分摆腰双足机器人结构的数据。机体整体高度约256cm，机器人的整体质量约为483.06g，上肢长约136cm，单臂长约90cm；机器人上半身的质量约为176.15g，下肢长约118cm，腿长约100cm，机器人下半身的质量约为306.91g。通过SolidWorks2014建立的三维简化仿真模型，如图2所示。

3 摆腰双足机器人运动学建模

根据摆腰双足机器人的结构原理，可以发现其主要依靠腰部的摆动使机器人本体的重心发生改变，在对其运动学研究过程中不可避免的需要涉及到在X、Y、Z三个方向的坐标。因此，选择更加有利于摆腰双足机器人轨迹设计的广义坐标法对机器人进行运动学建模，并且再此基础上应用ZMP原理分析机体在运动过程中的稳定性。

3.1 模型简化及运动模型的建立

摆腰双足机器人的左支撑脚的脚心为原点，向前运动的方向为X轴的正方向；向左摆动的方向为Y轴正方向；竖直向上为Z轴正方向，建立空间直角坐标系OXYZ[7]。

在进行正运动学分析之前，我们先进行几种假设：

（1）摆腰双足机器人在Y向摆动时只影响Y、Z两轴的方向的坐标，对X轴的影响忽略不计；（2）摆腰双足机器人腰部往上的部分在X轴方向的偏移始终竖直向上；（3）踝关节到脚掌的部分始终只受重力影响，方向竖直向下，并且关节的质量忽略不计。

结合假设将摆腰双足机器人简化为六连杆机构并建立运动学模型[8]。为了便于后面的描述和数据处理，将每个关节自由度从左到右依次编码。六连杆简化模型，如图3所示。

图3 六连杆简化模型Fig.3 A Simplified Model of Six Links

数字1～6为各连杆的编号，即数字1和6为摆腰双足机器人的脚踝关节；数字2和5为摆腰双足机器人的腿部；数字3为摆腰双足机器人的腰部；数字4为摆腰双足机器人的上身，小黑点为各杆件的质心。以左支撑脚的脚心在参考坐标系中的点（x1，y1，z1）为基准点。机器人模型计算较多，其中参数如下，式中：

mi—杆件i的质量，i=1，2，3，4，5，6；

li—杆件i的长度，i=1，2，3，4，5，6；

di—杆件i的质心到前一个关节点的距离，

i=1，2，3，4，5，6；

qi—广义角（杆件i与Z轴之间的夹角（取较小角），顺时针正，逆时针为负）；i=1，2，3，4，5，6。

假设在静止状态下质心坐标为（xc，yc，zc），根据质心公式：

由在静止状态下的质心定律可知，机器人整体在Z轴的质心坐标为103.74mm，机器人上半身在Z轴的质心坐标为187.45 mm，机器人下半身在Z轴的质心坐标为58.50mm，而由计算得到的机器人下半身在Z轴的质心坐标为55.6mm。与实际测量到的下半身在Z轴的质心数据对比，结果相近，可以作为摆腰双足机器人在运动学计算过程中的依据。

则，摆腰双足机器人在向前运动过程中其质心的变化：

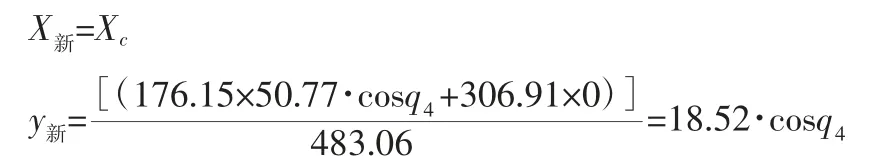
z新=［176.15×（50.77·sin q4+136.7）+306.91×58.5］/483.91注：q4—上半身左右摆动时与Y轴之间的夹角，向左为正。

设当上半身摆动时带动机器人整体的摆动，使机器人整体在Y方向发生的偏移角为θ，则：θ=arctan（y新/z新）

3.2 摆腰双足机器人坐标计算

式中部分公式进行简写，如：sin q2=s2，cos q2=c2；（xdi，ydi，zdi）—杆件i的质心在固定坐标系的坐标，i=1，2，3，4，5，6；

依次为摆腰双足机器人的支撑脚质心、支撑腿踝关节质心、髋关节质心、腰关节质心、上身躯干质心、摆动腿踝关节质心、摆动脚的质心坐标；

根据六连杆简化模型得到计算结果如下：

根据矩阵坐标对t求导的准则，对杆件i的质心的坐标逐项求导：

根据矩阵坐标对t求导的准则，对杆件i的质心的速度逐项求导：

根据摆腰双足机器人的结构原理可知：q1=0，q3=0，q6=0。

通过以上摆腰双足机器人正运动的计算，我们发现对摆腰双足机器人运动控制的过程中不涉及其逆运动学的计算，因此，不涉及其逆运动学的计算。如果需要计算逆运动学还需摆腰双足机器人各个关节的坐标值。

3.3 摆腰双足机器人稳定性分析

所设计的摆腰双足机器人，机构特殊，其ZMP多边形是由机器人本体重心限制所形成的一个在X、Y向的矩形区域。我们从机器人本体所需要完成的动作设计出发，找出两项限制条件。由于各个关节是由舵机驱动的，这两个限制的本质就是找到舵机最大转动角的范围。

在Y向，主要考虑重心偏移量的最大值。重心左右偏移时，为保证其不发生摔倒的现象，重心偏移不得超过腿部单腿的重心的位置，经过计算偏转角约为49°，考虑到摆动过程中的惯性力，重心左右偏移的范围不超过45°。

ZMP点的坐标公式为：

当竖直方向的加速度为0的时候，即简化为重心坐标。

将限定的极值结合正运动学方程带入到ZMP公式中，经行验证，所得结果落在支撑多边形的内部，说明只要在限定转角范围内进行运动，摆腰双足机器人的ZMP点坐标必然全程落在稳定区域内，不会发生摔倒等不良现象。运动仿真我们选择45°的情况。

3.4 摆腰双足机器人运动速度分析

根据极限位置假设，可以计算出摆腰双足机器人能达到的最大步长约为21.5mm。

根据舵机的转速0.17s/60°（4.8V）推导出1秒中内双足摆动次数约为7.5次，推导出双足摆动的最大的速度为42.2mm/s。根据对常见双足机器人运动速度的分析，这里设计的机构超出一般双足机器人的基本运行速度，本次机构设计理论上是可行。

4 运动仿真

假设摆腰双足机器人各个关节设为转动副并且存在关节摩擦，脚底板与地面之间存在碰撞摩擦力[10]。在摆腰双足机器人的各个关节上添加约束力。参考插值法插入驱动函数规则，验证q2=q5=45°，q4=15°情况下的运动情况，插值函数如下：

左臂转体曲线方程：

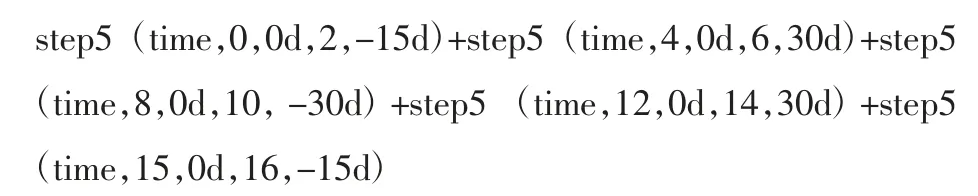
右臂转体曲线方程：

腰部转动角的曲线方程：

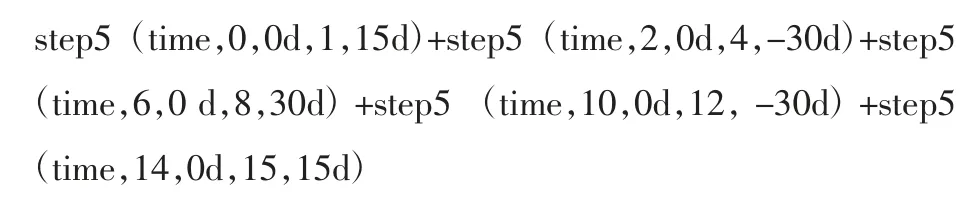
髋关节转动角的曲线方程：

在差值过程中，选取整值的差值时间，以便于观察机体在运动过程中的运动状态，但是在此过程中不免出现上下躯体一部分在运动，一部分停止的状态，要想改变只能在后续的控制过程中，逐步调整舵机的转动角度。左脚质心与右脚质心在X轴方向，16 s时间内的运动曲线，如图4所示。X轴的运动方向是机体整体向前运动的方向，在该轴向可以明确的表现机体向前运动的状况。

图4 左脚质心与右脚质心在x轴位置变化曲线Fig.4 Left and Right Foot X Axis Position Change Curve

从图中我们可以清晰的看出，左脚与右脚的质心运动的整体趋势是呈现阶梯状递升，说明机器人整体在X轴方向正在向前运动，而图中存在阶梯的原因则与插值时间有关。

机体在X、Y、Z轴的重心位置变化曲线，如图5所示。无论是在X轴、Y轴还是Z轴，其整体上都呈现出平稳的状态，证明摆腰双足机器人在运动过程中，机体基本保持稳定状态。存在波动是由于运动时机体震动等原因，而且对比图4可以发现，不稳定的状态大多存在于图4中的阶梯位置，说明需要对插值进行改进，但是对整体稳定性的评估没有影响。

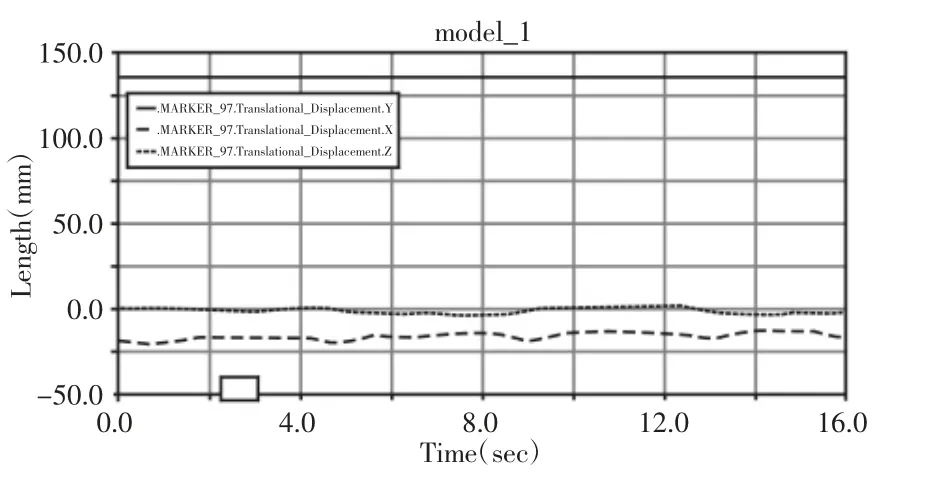
图5 重心位置变化曲线Fig.5 Center of Gravity Curve

5 结论

通过在ADAMS中对摆腰双足机器人仿真的结果，我们可以清楚地看出，自主创新设计的摆腰双足机器人在运动过程中可以保持基本的运动稳定，而在无膝的状态下，可以减少运动过程中，寻找重心的时间，可以大约提高（2～3）%的工作效率，满足设计的初衷，可以建立样机进行下一步的实验论证。