不同结构参数对深潜装置观察窗应力影响分析
孙德志,孙 飞
(吉林工程职业学院,吉林 四平 136000)
1 引言
载人潜水器作为重要的大型深海运载装备,是海洋科学技术发展的最前沿和制高点。深海载人潜水器是现代海底探查及研究的重要装备,观察窗使是其观察外界环境的重要途径。在满足安全性的前提条件下,观察窗优劣的评价标准主要就是其数量和它们之间视野的覆盖程度。文献[2]利用ABAQUS计算窗座围栏与球壳连接过渡处参数对于观察窗极限强度影响;文献[3]运用数值计算对大深度潜水器耐压球壳结构性能影响及稳定性分析;文献[4]结合模型试验和数值计算对大深度球形耐压结构静态力学性能进行研究;文献[5]认为由于观察窗设计是属于有限寿命设计,对于该尺寸以及深海高压的实验环境,又不可能提供满足试验方法的条件。
针对大深度载人潜航器进行静力学分析,对比分析三种结构即平圆形,锥台形,球扇形。基于有限元对影响观察窗的应力、应变和位移因素展开研究。对比分析因素对应力、应变和位移的影响,寻求观察窗最优设计。
2 观察窗受力分析
视窗的锥形面和窗座的锥形面尺寸相同,二者均进行了打磨处理,保持接触边界光滑[6]。观察窗三种基本结构:平圆形、锥台形和球扇形。球扇形是承受外界压力最理想的形式。观察窗在静水压作用下只承受压应力,而且分布均匀,数值较小。因此在同样厚径比情况下,球扇形观察窗较平圆形和锥台形观察窗有承压能力高,视野宽阔,人眼在球心时图像不会失真的优点。
锥台形是轴对称图形,下面探讨从中心轴出发,距离中心轴为R距离位置的受力,取受海水的承压面直径为R,厚度为x,由45°得到下底面直径为,则上面受压力为πR2q,下面受力为:

受力平衡得:
侧面受力设为F(力的方向向下为“+”)
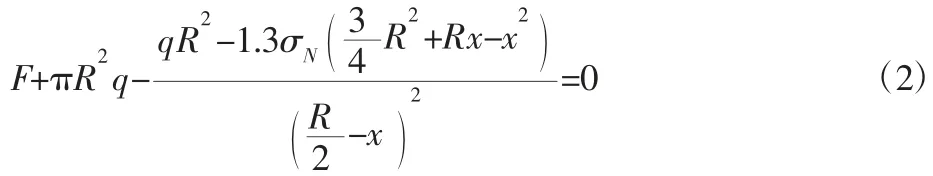
即得到距离R的侧面受力F等于:
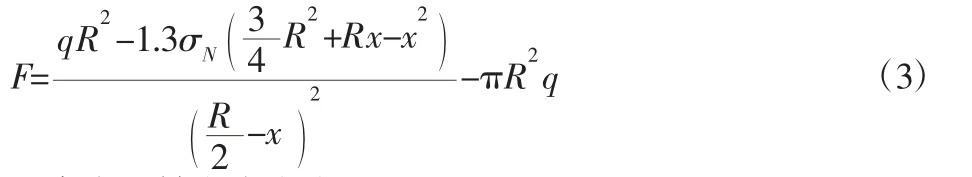
观察窗的轴向应力为:
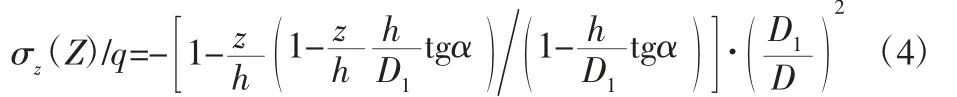
径向应力为:
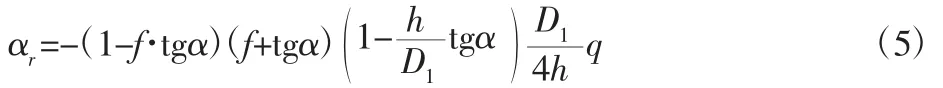
三个主应力为:

应力偏量为:

其中:

则,等效应力为:
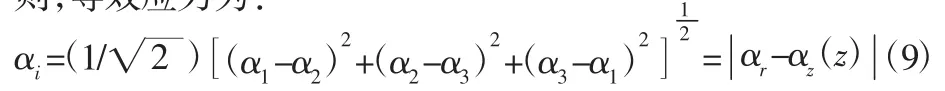
3 尺寸参数对观察窗影响分析
3.1 平圆形观察窗
保证外径与内径比值为3,分别取5组不同厚径比,建立平圆形观察窗的模型,具体如表1所示。
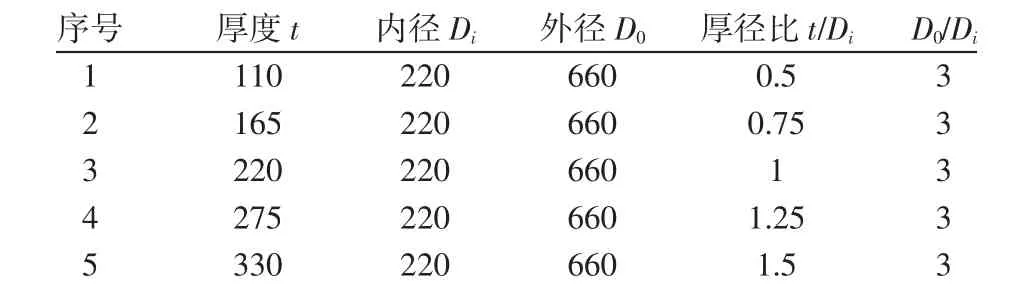
表1 不同厚径比的平圆形观察窗尺寸Tab.1 Flat Size of the Different Thickness Ratio
由于剪应力数值较小,不予考虑,环向应力的变化趋势与径向应力相同,故只取径向应力,轴向应力,径向位移,轴向位移在高压面、低压面、轴线的分布进行比较。
3.2 锥台形观察窗
3.2.1 锥角影响
保证厚径比值为1,取5组不同锥角的观察窗进行分析,具体数据,如表2所示。

表2 不同锥角的锥台形观察窗尺寸Tab.2 Different Cone Angle of the Cone-Shaped Observation Window
由于剪应力数值较小,不予考虑,环向应力的变化趋势与径向应力相同,故只取径向应力,轴向应力,径向位移,轴向位移在高压面、低压面、轴线的分布进行比较。
径向位移和轴向位移的数值也是随锥角的增大而减小,在90°以后减小的趋势逐渐平缓,值得注意的是径向位移在高压面上的分布,60°和90°两种锥台形观察窗的径向位移数值最小,而过小和过大的锥角都会使得径向位移的数值增加。
3.2.2 厚径比影响
保证锥角为90°,内径为220mm,分别取5组不同厚径比的观察窗进行分析,具体,如表3所示。通过有限元分析,不同厚径比的观察窗径向应力,轴向应力,径向位移,轴向位移在高压面、低压面、轴线的分布。
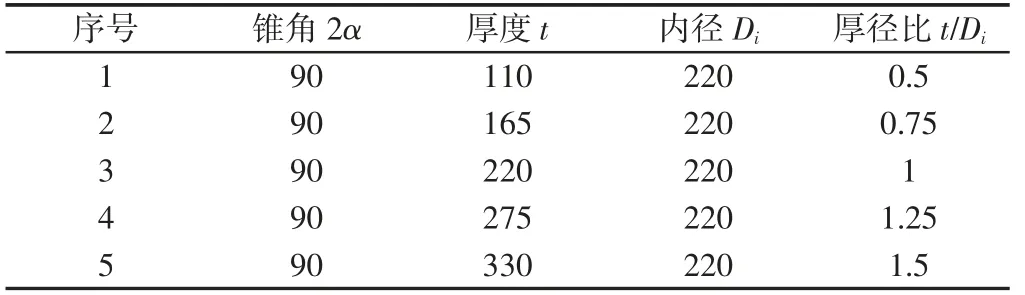
表3 不同厚径比的锥台形观察窗尺寸Tab.3 Different Thickness Ratio of the Cone-Shaped Observation Window Size
径向位移在高压面上的数值随着厚度的增加而增加,厚径比超过1以后径向位移会达到较大的数值。不同厚径比的观察窗的径向位移在低压面上的数值和分布趋势都大体相同。观察轴向位移在高压面上的分布,相对而言数值最小的是t/Di=1的情况,轴向位移在低压面的数值则是随着厚径比的增大而减小,减小的趋势在厚径比达到1以后逐渐平缓。这里要主要到轴向位移在轴线上的分布,除了厚径比为0.5和0.75两种情况下轴向位移的数值是随着z值的升高而单调降低外,其他三种均呈现出先减小后增大的现象,尽管厚窗(t/Di=1.5)的轴向位移数值在前半段较小,但是增大后的位移数值超过了厚径比为1.25和1两种情况。
3.3 球扇形观察窗
保证厚径比值为1,取5组不同锥角的观察窗进行分析,具体数据,如表4所示。
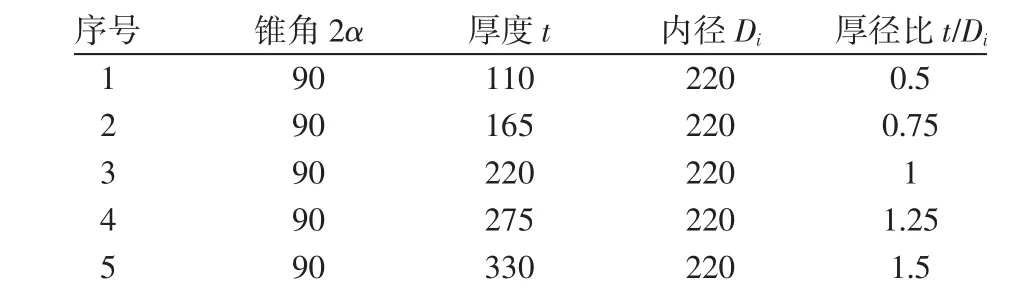
表4 不同厚径比的球扇形观察窗尺寸Tab.4 Different Thickness Ratio
通过有限元分析,得不同厚径比观察窗径向位移、径向应力、切向应力,如图1所示。径向位移、径向应力、切向应力的数值随锥角的增大而减小,在90°以后减小的趋势逐渐平缓。因此,同一厚度、相同厚径比的球扇形观察窗,锥角越大,其应力和位移的数值相对越小,但是这种减小的趋势在锥角达到90°后趋于平缓。
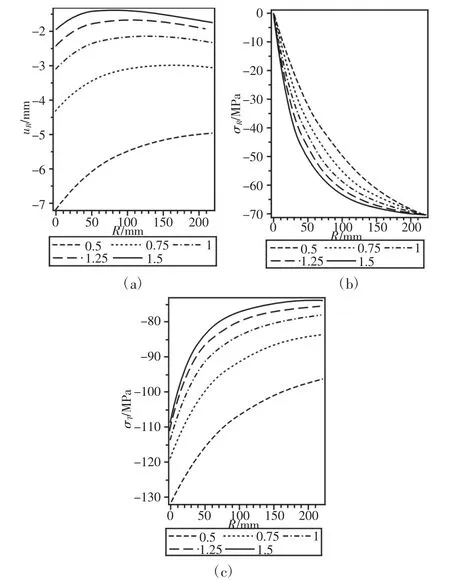
图1 厚径比对球扇形观察窗的影响Fig.1 The Effect of Thick and Small Ratio on the Fan-Shaped Window
3.4 观察窗结构形式的设计准则
取相同的厚径比、厚度、锥角,尺寸如表5所示。
表5 不同结构形式的观察窗尺寸Tab.5 Different Forms of Observation Window
平圆形和锥台形观察窗的径向应力和轴向应力在轴线上的分布,如图2所示。两种形式的轴向应力分布趋势大体相同,而径向应力虽然变化趋势相同,但是数值上有很大的差别,尽管平圆观察窗的高压面压应力数值要小于锥台形,但是平圆形观察窗的低压面出现了拉应力。可见,相同尺寸下,锥台形这种结构能够消除低压面中心处的拉应力。
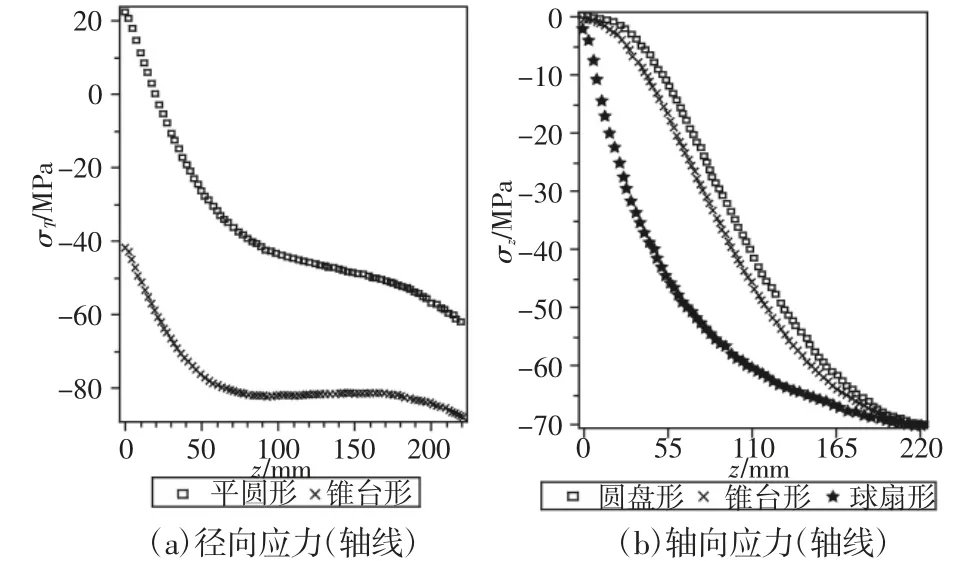
图2 结构形式对观察窗的影响Fig.2 The Effect of the Structure on the Observation Window
4 结论
基于有限元分析,对影响观察窗应力的尺寸参数和结构形式进行分析,对影响观察窗的应力、应变和位移的因素进行对比分析。结果可知:(1)对于平圆形观察窗而言,随着厚径比的增大,应力逐渐减小,当厚径比达到1之后,应力变化趋于平缓;(2)对于锥台形观察窗而言,随着锥角的增大,应力逐渐减小,当锥角达到90°之后,应力变化趋于平缓,随着厚径比的增大,应力逐渐减小,当厚径比达到1之后,应力变化趋于平缓;(3)对于球扇形观察窗而言,随着锥角的增大,应力逐渐减小,当锥角达到90°之后,应力变化趋于平缓,随着厚径比增大,应力逐渐减小,当厚径比达到1之后,应力变化趋于平缓;(4)三种结构形式中,球扇形观察窗应力状态最好。
———《扇形的认识》教学廖

