基于响应面法的数控铣床立柱多目标优化

郑 彬，张敬东

（攀枝花学院交通与汽车工程学院，四川 攀枝花 617000）

1 引言

立柱是数控铣床的重要支承部件之一，其结构性能对铣床的加工质量具有较大影响，主要包括抗振性、铣削精度和效率以及使用寿命等。因此，立柱的静动态特性决定数控铣床整机性能的重要指标之一。为确保数控机床实现高速、高效和高精度的设计要求，立柱必须具备较好的力学性能，其结构设计是以提高抗振和减轻重量为目的的多目标优化问题。

国内外很多学者都对立柱进行过相关的研究。文献[1]通过模态分析找出某复合加工机床立柱的薄弱之处，通过对立柱尺寸参数进行灵敏度分析并建立神经网络模型，使用遗传算法对其进行优化。文献[2]基于中心复合试验设计方法，建立了机床的最大变形、质量和一阶固有频率的响应面模型，采用非支配排序遗传算法对响应面模型进行多目标优化。文献[3]以某落地镗铣床立柱为研究对象，通过对其进行模态分析，得到立柱的振动特性，在不改变立柱主体结构的基础上进行拓扑优化，提高了立柱的第一阶固有频率。文献[4]针对某卧式加工中心的立柱，对立柱筋板形式加以改进，以提高主机动态刚度并减轻立柱质量。文献[5]针对某数控铣齿机床的立柱，通过采用不同的筋板厚度及布置方式，以减轻立柱重量为优化目标，进行了优化设计，最终使立柱减轻1.68t。以某数控铣床立柱为研究对象，借助于有限元分析软件ANSYS对立柱进行静动态特性分析，确定立柱薄弱环节。将立柱的第一阶固有频率、重量和最大变形定义为优化目标，在灵敏度与响应面分析的基础上，采用多目标优化算法对立柱的各设计参数进行优化，从而提高立柱静动态特性，为机床结构优化提供了一种新思路。

2 立柱静动态特性分析

2.1 立柱几何结构

立柱内部采用主筋、筋板和主筋板裙边结构，底部左右两侧分别有4个M22的螺栓与床身相连接。立柱正面有若干型号不同的螺纹孔，以便于安装和固定导轨、丝杆和丝杆螺母等部件，利用SolidWorks软件建立的立柱三维模型，如图1所示。

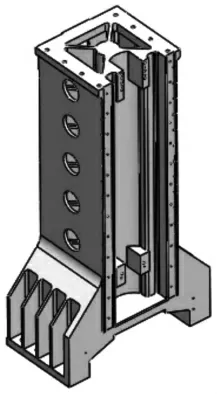
图1 立柱三维模型Fig.1 Three Dimensional Model of Column

2.2 立柱静力学分析

使用SolidWorks建立的立柱三维模型，包括了大量的螺纹孔、圆角和倒角等特征，但这些特征对立柱的静动态特性影响较小，忽略这些局部特征后，再导入至ANSYS[6]。对立柱进行网格划分时，采用四面体单元对立柱进行自由网格划分。立柱所使用的材料是灰铸铁HT300，密度为7300kg/m3，弹性模量130GPa，泊松比0.25。立柱的载荷包括：立柱自重、顶部横梁重量和主轴箱重量。立柱底部通过螺纹孔与床身相连接，将其设定为固定约束。最后进行有限元运算求解，其静力学分析结果，如图2所示。

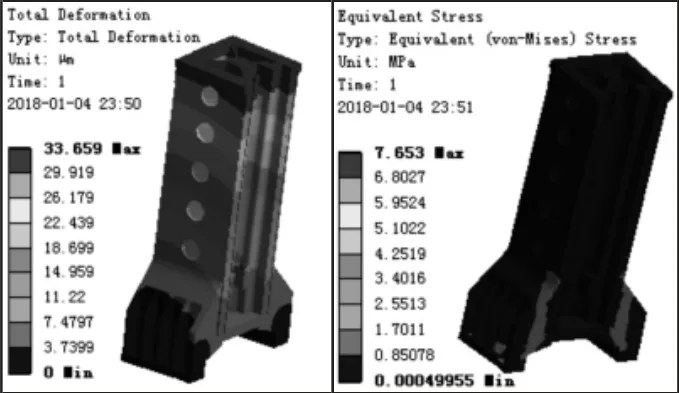
图2 立柱静力学分析结果Fig.2 Static Analysis Results of Column

由图2可知立柱的最大变形量为33.66μm，最大应力值为7.65MPa。立柱最大变形主要集中在立柱顶部与横梁相连接的部位，应力主要集中在底部支撑面和导轨安装面，并且立柱变形较大，对立柱优化时，需减少立柱的静态变形量。

2.3 立柱模态分析

使用ANSYS对立柱进行模态分析时，采用Block Lanczos（分块兰索斯）方法。立柱模态分析的约束条件和静力学分析时的约束条件一致，即将立柱底部螺纹孔设定为固定约束[7]。对其进行模态分析，提取立柱前六阶模态，其振型和各阶固有频率见，如表1所示。根据立柱的振型图和模态分析结果可知：立柱中间部位与外围圆周面是刚度较弱区域，多阶振型均在这些地方表现出最大振型。立柱的第一阶固有频率较低，因此需对立柱结构进行优化，以提高其固有频率改善其动态特性。

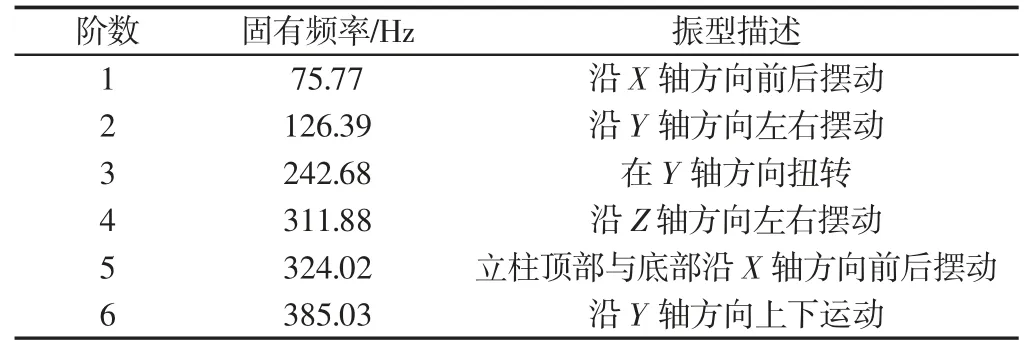
表1 立柱前6阶固有频率及振型描述Tab.1 First Six Order Natural Frequencies and Vibration Description of Column

3 立柱响应面建模

响应面设计方法是优化产品或工艺设计的一种方法，由文献[8-9]提出。其思想为：在确定输入输出变量的基础上，基于数学多项式作为基函数采用最小二乘回归法来得到输入变量和输出变量的映像关系，具有较好的可导性和良好的连续性，易寻优并且可采用常规数学优化方法进行求解。为构造立柱响应面模型，首先确定立柱的设计参数和输出参数，选择合理的试验设计方法，进行试验设计和灵敏度分析，从而构造出立柱的响应面模型[10]。

3.1 确定立柱设计参数

立柱主要由支撑主筋和厚度不等的主筋板和主筋板裙边组成，包括的尺寸参数较多，内部肋板结构复杂。结合机床设计人员建议，选取下述5个尺寸参数作为设计参数，如图3所示。其初始值，如表2所示。在不改变立柱原结构的基础上，基于机床设计指标，将上述设计参数的变化范围约定，如表2所示。

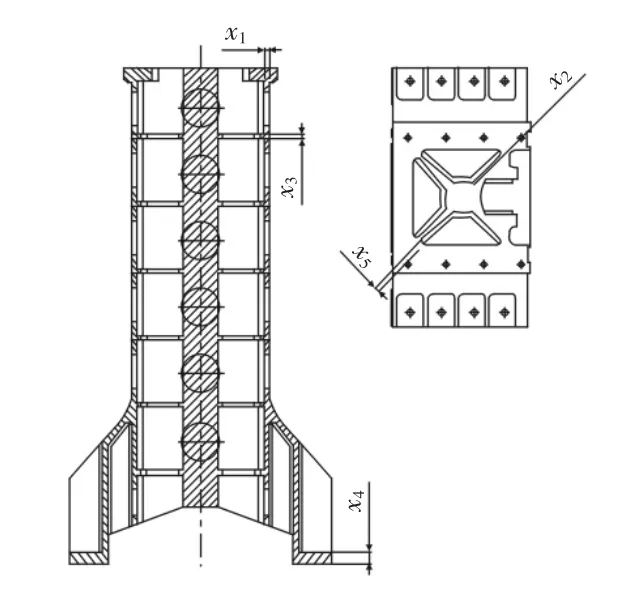
图3 立柱设计参数图Fig.3 Graphic of Column Design Parameters

表2 立柱设计参数（单位：mm）Tab.2 Design Parameters of Column（unit：mm）

3.2 DOE试验设计

对立柱的5个设计参数进行试验设计时，采用Box-Behnken试验设计方法，共有5个设计参数，因此样本点总数为41个。对立柱在初始设计条件下进行静力学分析和模态分析，将立柱的重量y1、静态最大变形量y2和第一阶固有频率y3定义为输出参数。进行试验设计后，需确定各设计变量对输出参数的影响程度，进而确定优化参数。采用灵敏度分析，可以确定各设计参数对输出参数的影响程度，从而选出灵敏度高的设计参数，忽略灵敏低的设计参数，提高分析效率，减少计算时间。将上述五个设计参数对立柱重量、最大变形和第一阶固有频率进行灵敏度分析，其分析结果，如图4所示。

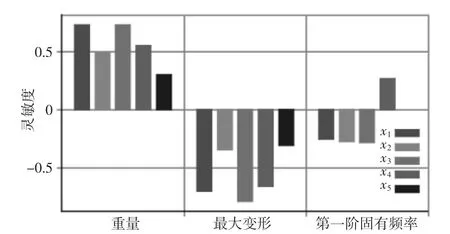
图4 立柱重量、最大变形和第一阶固有频率灵敏度图Fig.4 Sensitivity Graphic of Mass and Maximum Deformation and First Natural Frequency of Column

在图4中，当灵敏度为正值时，表示随着设计参数的增加，输出参数将增加；当灵敏度为负值时，表示随着设计参数的增加，输出参数将减小。由图4可知各设计参数对立柱的重量、最大变形和第一阶固有频率均具有较大影响，参数合适，不需要忽略任何参数。因此将上述五个设计参数均作为优化参数进行尺寸优化。

3.3 立柱响应面模型分析

考虑到共有五个设计参数，在建立响应面模型时，直接采用二次响应面模型，并考虑所有的二次项、一次项和各因素之间的交互作用[11]。在二次回归分析中采用后退法忽略影响不显著的设计参数和交互作用进行删除。所建立的二次响应面模型如式（1）、式（2）和式（3）所示。其中式（1）为设计参数与立柱重量的响应面模型；式（2）为设计参数与立柱最大变形的响应面模型；式（3）为设计参数与立柱第一阶固有频率的响应面模型。

构建响应面模型后，即可进行响应面分析，所建立的响应曲面如图5所示。其中，设计参数x2和x5对重量的响应曲面，如图5（a）所示。设计参数x1和x4对最大变形的响应曲面，如图5（b）所示。设计参数x3和x4对第一阶固有频率的响应曲面，如图5（c）所示。由图5可知，对立柱进行优化，需综合考虑各设计参数对立柱性能的影响程度，使立柱性能达到最佳。

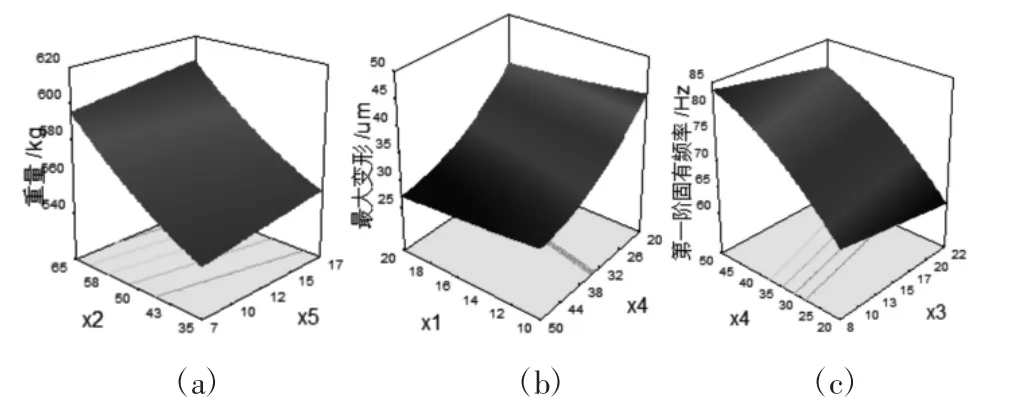
图5 立柱重量、最大变形和第一阶固有频率响应曲面Fig.5 Response Surface of Mass and Maximum Deformation and First Natural Frequency of Column

4 立柱优化设计

4.1 立柱多目标优化设计数学模型

当前，用于结构优化设计的主要方法是数学规划求解法。针对立柱优化问题，可采用下式表示：

求设计变量：

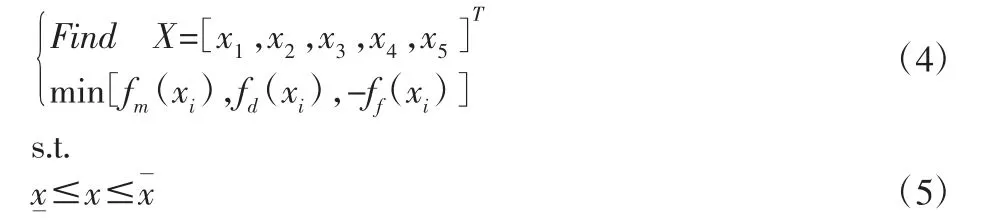
式中：x—设计变量；i—设计变量个数；min—求最小值；s.t.—subjectto的缩写，即约束于；f（x）—目标函数；x—设计变量下限；—设计变量上限。

其中，

X=［x1，x2，x3，x4，x5］T为立柱五个设计参数，其含义见表3。

fm（xi）=y1指对五个设计参数进行优化求解，使立柱重量最小化。

fd（xi）=y2指对五个设计参数进行优化求解，使立柱最大变形量最小化。

ff（xi）=y3指对五个设计参数进行优化求解，使立柱第一阶固有频率最大化。

4.2 基于遗传算法的多目标优化

以立柱重量最小化、最大变形量最小化和第一阶固有频率最大化为优化目标，采用多目标遗传算法进行求解。通过多目标遗传算法与帕累托法则进行计算后，获取一系列优化候选点，如表3所示。

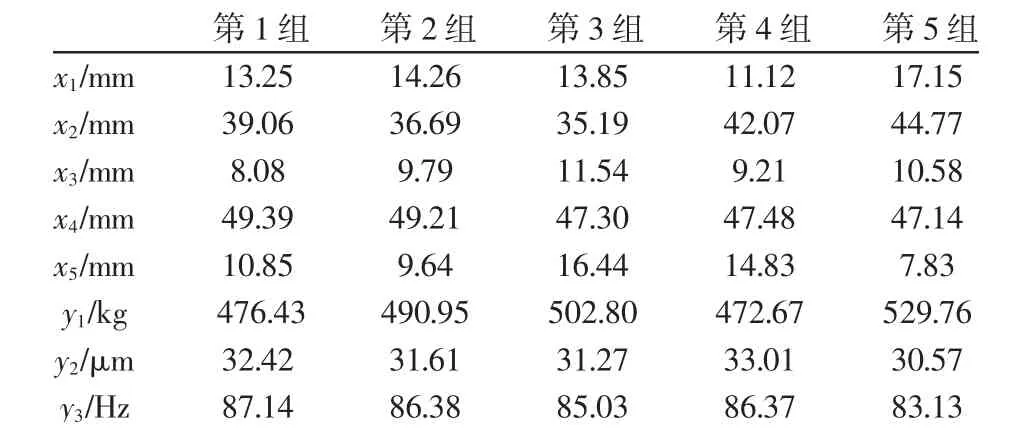
表3 五组最佳候选点Tab.3 Five Best Candidates

由表3可知：第2组优化候选点在重量上大幅减小，第一阶固有频率明显提高，静态变形量也适当减小。故综合考虑，选择第2组优化候选点为最优设计点。最终的优化结果如下：对立柱结构进行优化后，重量从最初的545.61kg减少至490.95kg，减幅11.1%。优化后立柱最大变形为31.61μm，原立柱最大变形为33.66μm，经优化后立柱最大变形量减幅6.5%。优化后立柱第一阶固有频率分别为86.38Hz，而原结构分别为75.77Hz，优化后立柱第一阶固有频率增加了14%。

5 结论

（1）以某数控铣床立柱为研究对象，进行静力学与模态分析，得到立柱的最大变形云图、应力云图及前六阶固有频率及振型，找出立柱的薄弱环节，为立柱结构优化提供依据。

（2）对立柱主筋半径、筋板厚度和壁厚等进行Box-Behnken试验设计与灵敏度分析，研究了各设计参数对立柱重量、最大变形和第一阶固有频率的影响程度，并建立其响应面模型。

（3）以降低立柱最大变形、减重和提高第一阶固有频率为优化目标，采用多目标优化算法对立柱设计参数进行优化并得到最优解。结合机床生产工艺及制造条件选择一组最优解，优化效果明显。为机床的功能部件或整机优化提供了一个参考方案。