CFM56-3发动机高压点火导线可靠性分析

孔祥芬，蔡峻青，张利寒，王国东

（1.中国民航大学航空工程学院，天津300300；2.郑州航空工业管理学院，河南 郑州 450000）

1 引言

航空发动机是飞机的心脏，具有高可靠性要求和高成本费用的特点，其健康状况对保证飞行安全和降低航空公司运营成本具有重要影响。高压点火导线工作在高温、强振动的环境中[1]，作为发动机故障率较高的一个部件，其工作的可靠性直接影响发动机的功率、经济性和发动机工作的可靠性[2]。此外，随着航空公司的机队逐步进入老龄期，要求更多的维修维护以及人力物力投入以达到持续适航的要求[3]。因此，在保障发动机的性能可靠性的同时，努力降低发动机维修成本与发动机运营成本，是航空公司必须要解决的难题。

目前国内外专家学者对飞机系统或部件的可靠性问题已经进行了大量的研究。针对航空发动机具有多种失效模式的特点，文献[4]采用贝叶斯模型平均的方法对航空发动机可靠性进行集成分析，并通过算例验证了多模型集成可靠性技术在对复杂系统进行可靠性分析时更为精确有效；文献[5]研究了多种故障模式对航空发动机转子叶片的影响，并将环境因素引入模型中使模型更接近实际情况。在可靠性分析新方法的提出问题上，文献[6]为了更准确的研究变形和应力对航空发动机叶盘性能的影响，在湍流模型理论和叶盘流场模型的基础上，提出一种在保证计算精度的前提下计算效率更高的双重极值响应面法；文献[7]为确定维修间隔，利用燃气涡轮发动机运行中的故障和维修数据，提出了基于风险的维修和剩余寿命评估的定量模型并获得最低运行成本下的最优维修间隔。在可靠性分析手段的优化问题上，文献[8]针对航空电子设备有替换I型截尾实验无失效的情形，提出了一种改进综合E-Bayesain法用于可靠性参数的综合评估；文献[9]在飞机电静液作动器的可靠性分析中，验证表明GO-FLOW法在减小计算复杂度方面较GO法有优势。尽管现在对飞机系统及部件的可靠性分析已经做了大量的工作，然而对发动机高压点火导线的分析研究还是很少的，因此采用可靠性理论对其进行分析有现实意义。根据XX航空公司的实际运营数据，采用假设检验的方法对CFM56-3涡扇发动机高压点火导线故障数据（平均无故障间隔时间）进行可靠性分析，并给出相应的维修建议。

2 数据采集与处理

采集国内XX航空公司波音737-300机队的CFM56-3涡扇发动机高压点火导线故障记录数据作为原始数据。由于数据不仅仅是来源于一台发动机，故需要根据需求对数据进行归类整合并检查剔除异常值。此外，采集到的数据有些根据飞行循环定义，有些是根据飞行小时定义，因此，将故障数据统一为用飞行小时定义，从而得到可靠性指标故障间隔时间。将故障间隔时间从小到大按升序排列，如表1所示。

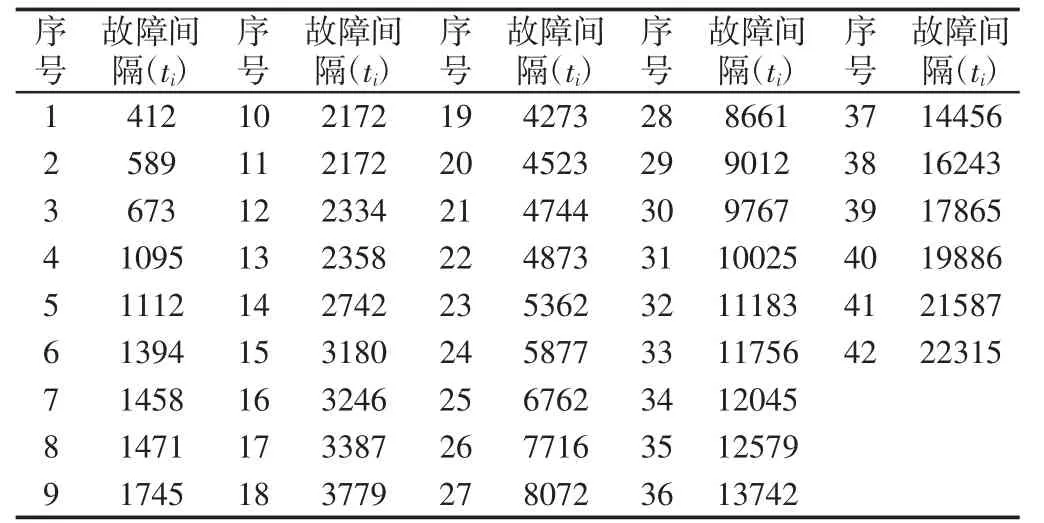
表1 高压点火导线故障数据（单位：飞行小时）Tab.1 High-Voltage Ignition Wire Fault Data（Unit：Flight Hours）

直方图可以从集中趋势、离散趋势及分布形态三个方面描述数据分布特征，对总体的分布特征进行推断。对表1的故障间隔时间以2500飞行小时为间隔进行分组，绘制高压点火导线故障数据频数分布直方图，如图1所示。观察图1的数据分布趋势，结合可靠性分析常用分布模型，初步预测波音737-300机型CFM56-3涡扇发动机高压点火导线故障数据分布符合指数分布、正态分布、对数正态分布和两参数威布尔分布。

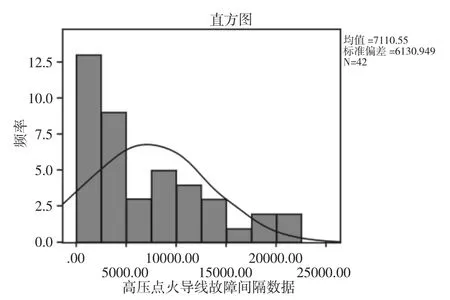
图1 高压点火导线故障数据直方图Fig.1 Histogram of High-Voltage Ignition Wire Fault Data

3 参数估计与检验

3.1 相关理论

参数估计是根据从整体中抽取的样本估计总体分布中包含的未知参数的方法，分为点估计和区间估计两部分，构造点估计常用的方法有矩估计法、极大似然估计法、最小二乘法以及贝叶斯估计法等，由于极大似然估计法可以估计较为复杂的参数，且能够充分利用整体分布的类型，故选用该方法进行参数估计。

极大似然估计法（MLE）最早由德国数学家高斯提出，后由英国统计学家R.A.Fisher正式推广[10]。初选的分布模型中，待估计参数具体为指数分布的参数λ，正态分布的均值μ和标准差σ，对数正态分布的对数均值μ和对数标准差σ，两参数威布尔分布的尺度参数η和形状参数β。

对于指数分布，参数λ的极大似然估计为：

正态分布中μ和σ2的极大似然估计分别为：

对于对数正态分布，可根据正态分布的参数估计得到μ和σ2的极大似然估计量分别为：

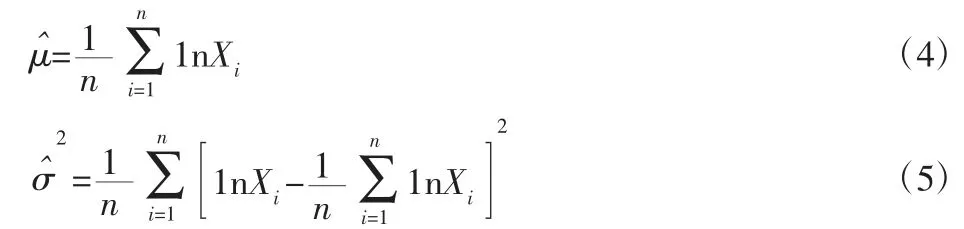
对于双参数威布尔分布，其参数的极大似然估计由如下超越方程迭代求解：

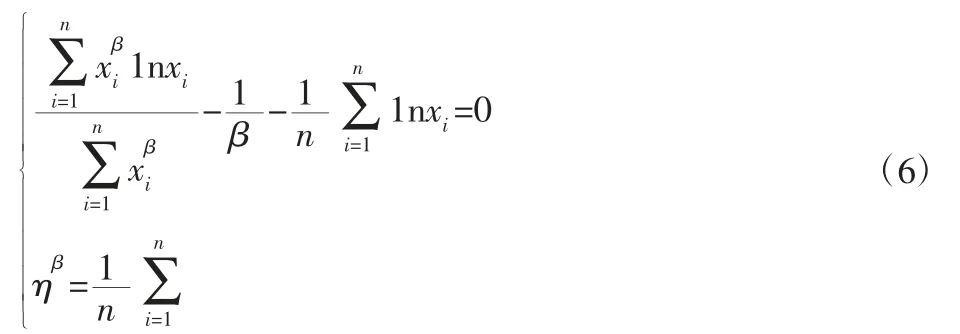
常用的分布模型检验方法有皮尔逊χ2检验、柯尔莫哥洛夫-斯米尔洛夫检验（简称K-S检验）、Shapiro-Wilk检验等，其中皮尔逊χ2检验可用于大样本或随机截尾数据的情况；K-S检验主要适用于连续型分布，可用于完全数据或定时、定数截尾数据的情况；文献[11]检验主要用于进行正态性检验。考虑到飞机发动机部件故障数据的特点，选用K-S检验法。

3.2 参数估计与检验步骤

基于极大似然估计法，利用MATLAB软件编程计算各备选分布函数对应的未知参数，具体为指数分布的参数λ，正态分布的均值μ和标准差σ，对数正态分布的对数均值μ和对数标准差σ以及两参数威布尔分布的尺度参数η和形状参数β。求出未知参数后，在Minitab软件中利用K-S检验法对各备选分布函数进行拟合优度检验。比较各分布统计量观察值Dn以及统计量临界值Dn，α，若统计量观察值小于统计量临界值，则接受该分布，反之拒绝。在都被接受的分布中，统计量观察值Dn较小的分布拟合效果比较好，更符合实际情况。若统计量观察值比较接近且接受概率P值相差不大，则进一步利用Minitab软件绘制相应的概率图，最终验证数据的分布类型。

3.3 参数估计与检验实例过程

按照上述模型参数的估计方法，根据表1中所记载的故障间隔数据，可以分别求出分布模型参数的极大似然估计值，如表2所示。

表2 高压点火导线寿命分布参数估计Tab.2 Estimation of High-Voltage Ignition Wire Life Distribution Parameters

采用Minitab统计分析软件进行K-S检验，将显著性水平α取为0.05，得出检验结果，如表3所示。

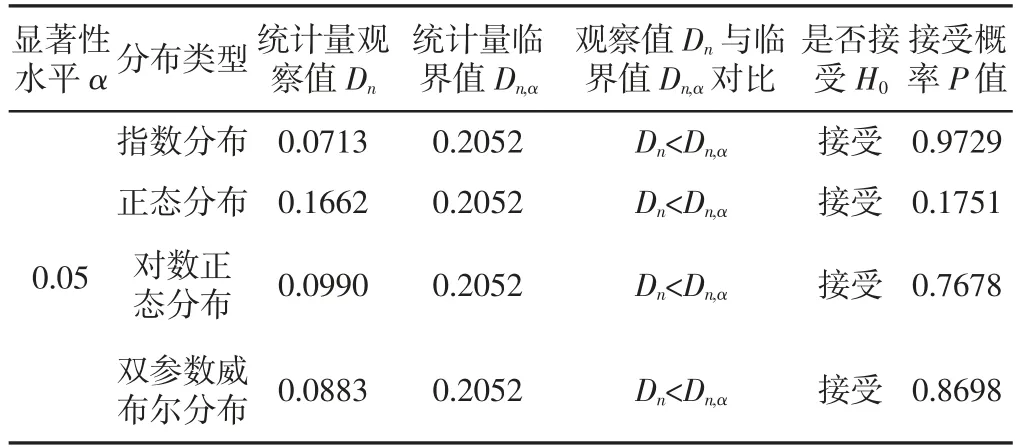
表3 高压点火导线寿命分布K-S检验结果Tab.3 K-S Test Results of High-Voltage Ignition Wire Life Distribution

由表3可知，根据直方图判断的四个分布模型全部通过了K-S检验。考虑其统计量观察值，指数分布、对数正态分布以及双参数威布尔分布均较小，证明这三个分布经验分布与理论分布拟合情况较好。而正态分布统计量观察值相对较大，且接受概率p值很低，同时正态概率图形与直线也有较大差异，表示其拟合情况不是很好。

进一步利用Minitab软件对备选分布进行拟合优度检验，得出拟合结果，如图2所示。

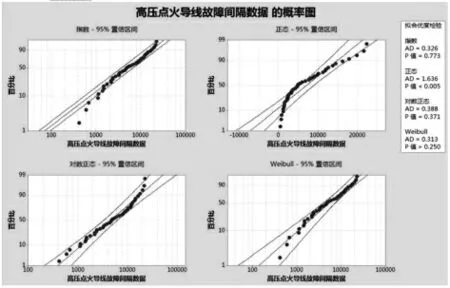
图2 拟合优度检验Fig.2 Goodness of Fit Test

由图2可知，除正态分布外，指数分布、对数正态分布、双参数威布尔分布的p值均大于显著性0.05，表明这三种分布假设均成立。但是指数分布的p值在三种分布中最大，高达0.773。并且根据似然比检验结果，指数分布优于对数正态分布以及双参数威布尔分布。考虑到在K-S检验中指数分布统计量观察值最小且接受概率值最大，也说明用指数分布表示高压点火导线故障间隔数据更为适合。因此，有理由认为高压点火导线的故障间隔数据服从指数分布是合理的，其失效率λ为0.00014，平均寿命为7110.5h。

4 高压点火导线寿命分布可靠性分析

CFM56-3涡扇发动机高压点火导线故障数据服从指数分布，失效率等于0.00014，为一常数，故障类型为偶然故障。用MATLAB绘制表示波音737-300机型CFM56-3涡扇发动机高压点火导线故障指数分布的可靠度曲线，如图3所示。

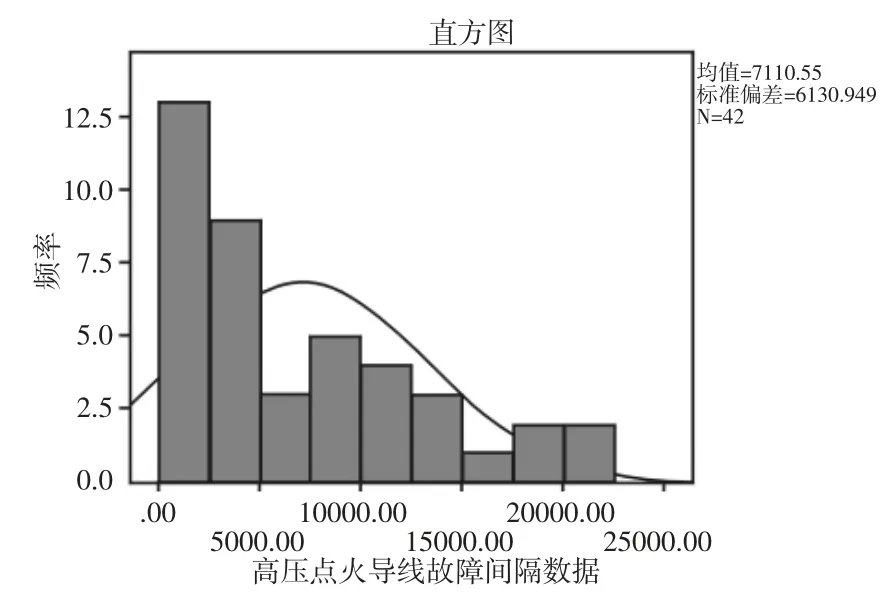
图3 高压点火导线可靠度曲线Fig.3 High-Voltage Ignition Wire Reliability Curve

由图3可知，高压点火导线的可靠性从开始急速下降，15000Fh之后趋于缓和。假设CFM56-3涡扇发动机高压点火导线已工作1589Fh，则现在的使用可靠度为R（1589）=0.8005，这表明每10台CFM56-3涡扇发动机在工作1589飞行小时后大约有2台发动机的高压点火导线会出现问题。飞机工作到中位寿命飞行小时4953Fh时，可靠度R（4953）=0.4999，与中位寿命的可靠度0.5很接近。当飞行小时约等于特征寿命，即为7158Fh时，可靠度R（7158）=0.3671，与特征寿命的可靠度0.3679相差不大，符合部件工作到特征寿命时，大约有63.2%的概率故障。若CFM56-3涡扇发动机需要高压点火导线可靠度达到90%以上，高压点火导线工作约需工作753Fh。若需要高压点火导线可靠度达到99%，则工作72Fh后就必须进行检修。

高压点火导线是发动机点火系统的一部分，根据某航空公司75架飞机2006年到2015年的700条维修记录整理发现，点火系统主要故障为点火电嘴和点火导线故障。根据飞机维修手册的描述，可以将点火系统视为热贮备系统。假设点火系统故障完全由高压点火导线故障导致，求出不同飞行小时下的可靠度以及不同可靠度下的工作时间，如表4、表5所示。

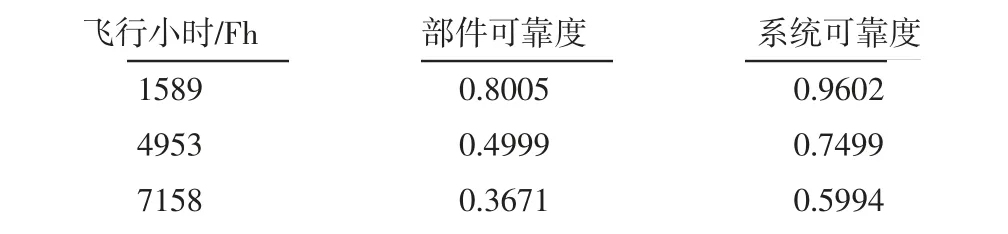
表4 不同飞行小时下部件及系统可靠度Tab.4 The Component and System Reliability Under Different Flight Hours

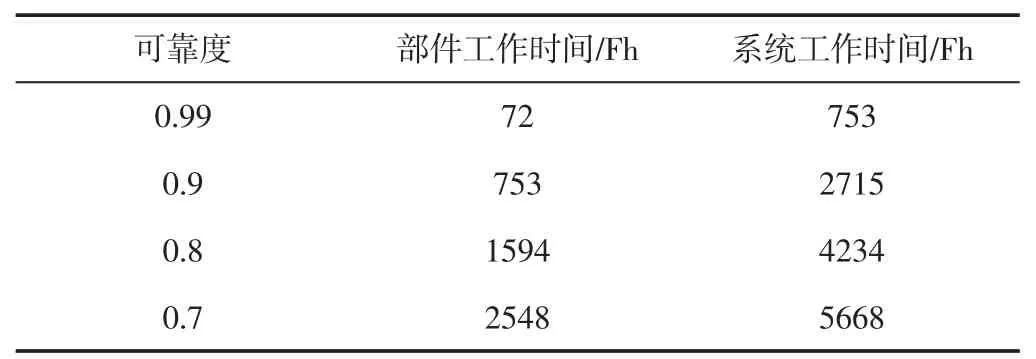
表5 不同可靠度下部件及系统工作时间Tab.5 The Com ponent and System Working Hours Under Different Reliability

由表4可知，在热贮备的条件下，经过1589Fh后，单台CFM56-3发动机点火系统的系统可靠度R（1589）=0.9602。由表5可知，作为热贮备系统的点火系统可靠度在90%时，CFM56-3涡扇发动机约需经过2715Fh才可能出现故障。若是航空公司对于点火系统的可靠性要求达到99%，则753Fh之后就必须对高压点火导线进行检修。

由于故障类型为偶然故障，在此阶段对系统进行定时维修不合适，采用视情维修或状态监控更合适[12]。鉴于飞机维修手册中对于右点火系统具有更高重要度的情况，假设航空公司需求其具有99%可靠度，建议在72Fh之后就开始密切关注右点火系统高压点火导线工作状态。通常情况下，状态检修周期Tm=0.10MTBF，指数分布MTBF（平均无故障工作时间）为参数λ的倒数，即7110.5Fh，则状态检测周期Tm约为711Fh，与系统可靠度99%所需经过的工作时间753Fh很接近，因此建议每隔711Fh左右，对整个点火系统进行状态检测。

5 结语

（1）针对航空发动机高压点火导线缺乏可靠性分析的问题，提出采用可靠性理论中假设检验的方法对其进行研究，介绍了其基本思想，并基于国内XX航空公司波音737-300机队的CFM56-3涡扇发动机高压点火导线故障记录数据，论证了该方法的有效性。

（2）通过对CFM56-3涡扇发动机高压点火导线故障记录数据的可靠性分析，得出了高压点火导线的寿命分布特征，即服从指数分布，其失效率λ为0.00014。

（3）考虑到实际情况下CFM56-3涡扇发动机拥有左点火系统及右点火系统各一套，但右点火系统具有更高的重要度，建议72Fh之后对右点火系统高压点火导线进行状态监控密切关注其运行状态，并且每隔711飞行小时，对整个点火系统进行状态检测。

（4）这里的研究方法来源于可靠性基础理论与经典统计理论的结合，不仅可以用于飞机中的系统、子系统及其部件，还可以为其他领域设备的寿命分布研究和可靠性分析提供参考。