耐压结构观察窗应力分析
王欢欢 曾子健
(中国石油大学(北京),北京 102249)
耐压结构观察窗应力分析
王欢欢曾子健
(中国石油大学(北京),北京 102249)
本文首先介绍典型的锥台的耐压观察窗以及观察窗模型的基本假定,然后以锥台型观察窗结构为重点进行理论应力分析。最后利用ANSYS软件,结合有限元计算分析,对比理论计算和有限元计算结果的差异。本文的研究成果对于耐压结构观察窗的设计具有一定的参考价值。
深海潜水器 观察窗 应力分析 耐压结构 ANSYS有限元
引言
探索和开发海洋的运载工具包括深海潜水器,而大深度耐压结构的设计研制又是深海潜水器的关键技术之一。深水情况下,压力是不可忽视的外力。在深水条件下观察窗的受力稳定与刚度又是重中之重。文献[1]对潜水器观察窗进行了计算和试验两方面的研究,文献[2]则对观察窗应力进行了理论分析,但文献[2]假设观察窗应力均匀分布。本文对观察窗应力从理论和计算两方面作了进一步探索,给出一个更为合理的观察窗应力计算公式。文章首先介绍典型的锥台型耐压观察窗以及观察窗模型的基本假定,然后以锥台型观察窗结构为重点进行理论应力分析。最后利用ANSYS软件,结合有限元计算分析,对比理论计算和有限元计算结果的差异。
1 观察窗结构概述
耐压观察窗根据结构形式的不同,一般分为3类:锥台型观察窗(conical acrylic windows)、平圆形观察窗(flat disc acrylic windows)和球扇形观察窗(spherical shell acrylic windows)。而根据其不同的承载形式,它又可以分为:双向承压、单向承压。虽然观察窗的形式多种多样,但是潜水器观察窗在实际设计中最常用的结构形式是带锥面的球扇形观察窗和单向受压的锥台型观察窗。下面主要研究单向受的锥台型观察窗的理论分析。
1.1锥台型观察窗
锥台型观察窗(如1图所示)与窗座的接触面为锥台面。在外界的压力作用下,因为接触面是锥台面,所以观察窗与窗座之间的密封性能很好。而且,这样的结构使得观察窗内部的应力主要为压应力,又因观察窗材料的抗压性能远远超过抗拉性能,所以这对观察窗的设计与使用十分有利。潜水器观察窗一般采用90°圆锥度角的结构进行设计。

图1 锥台型观察窗示意图
1.2观察窗模型的基本假定
为了方便观察窗应力的分析研究,对观察窗模型作出下列基本假定[3]。
(1)均质性假定:假设观察材料材质均匀;
(2)连续性假定:假设观察窗材料是连续介质;
(3)完全弹性假定:假设观察窗的变形发生在弹性范围内;
(4)各向同性假定:假设观察窗在各个不同方向上的物理力学性质相同;
(5)小变形假定:假设观察窗的形变量与自身几何尺寸相比属于高阶小量;
(6)无初始应力假定:假设当无外力作用时,观察窗内部没有应力,处于自然状态。
2 锥台型观察窗的理论分析
锥台型观察窗是一个轴对称的三维物体。根据轴对称原理,假定在观察窗内任何一点所受的径向力相同,所以可以简化成平面问题。该问题的特点为观察窗所受的体力、面力以及应力都与某一个坐标轴无关,即通过旋转方向向下的z轴的任意平面切割成的观察窗平面上的体力、面力以及应力大小都是相等的。因为观察窗的轴对称性,其径向的受力平衡自动满足。
2.1观察窗的尺寸设计、边界条件及荷载
锥台型观察窗的尺寸设计如图2所示,用D1、D2和h分别表示观察窗的外直径、内直径和厚度,锥体倾角为α。在外径面上,潜水器外压为q。因为接触边界非常光滑,假设圆锥台的应力均匀分布,在边缘很小范围内过渡到0,过渡段的应力忽略不计。观察窗与窗座接触的圆锥面上受到的接触正压力和摩擦剪应力分别为和,且其之间的摩擦系数为,受力如图3所示。
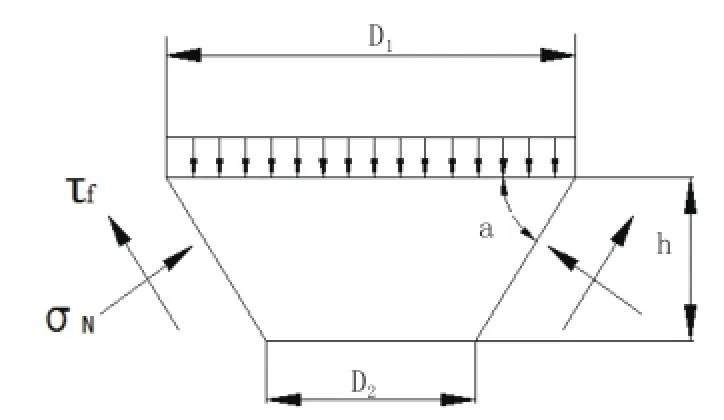
图2 锥台型观察窗尺寸设计

图3 锥台型观察窗受力情况
2.2.1观察窗侧向正压力和摩擦剪应力
圆锥台表面积为:

由锥台平衡可得:
所以接触正压力为:


由式(4)和式(3)式得:

2.2.2观察窗轴向应力
取一段高为z的锥台,受力图见图4。

图4 观察窗轴向应力
由锥台平衡可以得:
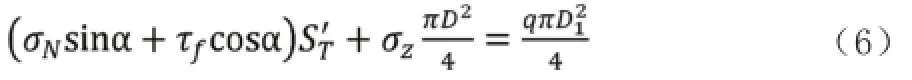
其中,高为z的锥台表面积

所以,

那么,观察窗轴向应力为:
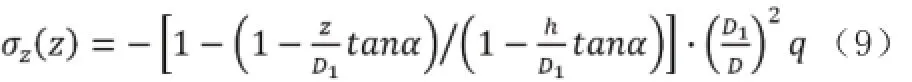
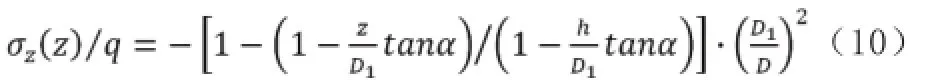
2.2.3观察窗径向应力
因为是轴对称问题,所以径向应力一定是均匀分布的。
取斜面任意一点,其应力状态如图5所示。
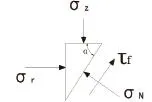
图5 观察窗径向应力分析
根据平衡条件可得:

由式(11)和式(4)、(5)可得:

2.3理论分析总结
到此,锥台型观察窗的摩擦剪应力、侧向压应力、径向应力和轴向应力可以分别由式(5)、(4)、(12)和(10)四个表达式计算。改变观察窗的参数(外表面直径D1、摩擦系数、厚度和锥度),就可以分析锥台型观察窗的应力状态随这些参数的变化情况,进而从理论上对锥台型观察窗的结构设计进行优化。
3 ANSYS有限元分析
3.1 参数设置
通过有限元数值计算可以对整个观察窗的应力进行数值模拟。观察窗尺寸参数:D1=640mm,D2=200mm,h=220mm,α=45°;观察窗材料属性:弹性模量为2780MPa,泊松比为0.38。观察窗与窗座的边界摩擦系数为=0.1,外荷载为70MPa。
3.2建立模型及划分网格
建立锥形台形式的模型如图6所示。本模型采用正三角形单元进行划分有限元单元格,划分之后的网格图见图7。

图6 观察窗模型

图7 观察窗网格划分
3.3ANSYS求解应力
根据设定的模型施加约束条件并且进行加载,最后进行数值有限元计算,可以得出观察窗受压变形量,如图8所示。同时,还可以求得径向应力与轴向应力的分布特点,如图9所示。

图8 变形位移等值线

图9 应力分布特点图
3.4理论分析与ANSYS求解对比
将D1、D2等参数代入式(9)和式(12),可得观察窗对称轴直线上轴向应力和径向应力随Z变化的理论曲线,再将对称轴上各有限元节点处的数值与理论值进行对比,结果如图10所示。图中实线为公式(9)给出的结果,方点为有限元计算的结果。对比理论计算和有限元计算结果可知,二者基本是相符的。

图10 轴向应力在对称线处对比图
4 结论
本文针对深海耐压结构的观察窗,得出了结构观察窗应力的理论计算方法。此方法以观察窗的锥度、外表面直径、内表面直径、摩擦系数和厚度为基本参数,计算不同形式观察窗的应力,从而为深海耐压结构观察窗这类结构的优化奠定理论基础。同时,本文对观察窗进行ANSYS有限元分析,并与理论分析进行对比,发现两个结果基本相符。可见,本文的研究可以为深海耐压结构设计优化和制定相关技术标准提供一定的理论依据。
[1]刘道启,胡勇,王芳,田常录,崔维成.载人深潜器观察窗的力学性能[J].船舶力学,2010,(7):782-788.
[2]刘道奇,胡勇,田常录,崔维成.深海耐压结构观察窗应力分析[J].船舶力学,2010,(2):121-125.
[3]岳坤.深海前期开口结构界面变形协调的研究[D].无锡:江南大学,2011.
Stress Analysis on Deep-sea Structure’s Viewport Windows
WANG Huanhuan,ZENG Zijian
(China University of Petroleum-Beijing, Beijing 102249)
The s tructural des ign of pres surized deep-s ea vehicle with large opening id one of the key problems for technique developing of dep-sea exploration equipments. The theoretical and comp-tational stress analysis of the viewport window id carried out in this paper, and th method of stress c alculation and structural optimization is inves tigated. The conclusion of this paper are meaningful for the design of view port structures.
deep-s ea s ubmersible, view port windows,stress analysis,non-metal material,pressure structures

