基于遗传算法的大型泵站工程安全综合评价模型研究

齐金奎

(绍兴市第一水利生态建设有限公司,浙江 绍兴 312000)

1 研究方法

1.1 遗传算法

遗传算法(Genetic Algorithm，GA)是由美国Michigan大学的John H.Holland于20世纪60年代末到70年代初受生物进化论启发而提出的，其来源于自然界生物进化过程，通过自然的选择淘汰、遗传、变异进化，最终产生能够适应环境变化的合适个体。遗传算法是在生物自然选择和遗传基础上进行随机搜索的一种有效算法，其具有较强的鲁棒性、自适应性和高效性。

遗传算法在工程领域得到广泛应用，模型的优化问题目标为：

(1)

式中：f为优化准则函数；C={cj}为模型p个待优化参数；[aj,bj]为cj的初始变化区间；X为模型N维输入向量；Y为模型M维输入向量；F为般非线性模型，即F：RN→RM；‖‖为取范数；q为实常数，如q取1时为最小一乘准则，q取2时为最小二乘准则，等等，根据实际模型进行设定。

在设计遗传算法时，常从以下几方面设计：染色体编码方式、种群初始化、确定适应度函数、选择、交叉、变异和算法停止准则。遗传算法流程图，如图1所示。

图1 遗传算法流程

步骤1：二进制编码。遗传算法中对染色体编码方式的选择十分重要，它也是设计染色体的关键。染色体的结构是由其编码方式决定的，而且染色体的编码方式也会对后续遗传产生重大影响。通常在选择染色体的编码方式时，要充分考虑到所研究问题的性质，它将直接影响编码方式，进而影响到整个模型的求解效率。常用的编码方式有实数编码和二进制编码[1]。二进制编码是使用二进制字符0和1的长字符串来表示传统的实数值。遗传算法中的个体用固定长度的二进制符号串来表示，在编码过程中，二进制编码交叉操作的搜索能力强于十进制编码。

步骤2：随机生成初始父代种群。设群体规模大小为n。当种群数量过大，将增加适应度值等的计算量；种群数量过小，迭代次数会增大，而且容易陷入局部极小点，对于种群规模的选取，要根据实际问题来确定[发2]。

步骤3：父代个体适应度的评价。适应度是对遗传算法中每个个体的适应生存能力进行表述，任意个体都都有一个适应度值与其对应，即将父代种群中的cj(i)代入式(1)得相应的优化准则函数值fi。fi的值与该个体的适应度值呈负相关。因此第i个父代个体的适应度函数值为：

(2)

式中：为避免fi为0，设置分母中“0.001”。

步骤4：父代个体的概率选择。取比例选择方式，因此个体i的选择概率为

(3)

在父代群体中以概率pi对第i个个体进行选择，如果适应度高就有较大机会保留到自带个体中，适应度低的个体有较大概率被淘汰，以此构成包含n个个体的子代种群。

步骤5：父代个体的交叉操作。由步骤4得到的n个个体两两配成n/2对双亲。以交叉概率pc选取两条父代个体，从中随机选取两位置cs1和cs2，然后对cs1和cs2之间的基因进行交换，产生两个新的子代个体，如图2所示。

图2 两点交叉操作示意图

步骤6：子代个体的变异。对子代个体，以变异概率随pm机对某条父代个体中的任意基因值进行改变，即基因值由0的变为1，基因值由1的变为0。与生物界遗传变异一样，在遗传算法中变异发生的概率非常的低，常设置的取值范围是pm=0.00-0.05。

步骤7：停止准则。停止准则和所研究的问题相关，常见的停止准则有两种：最大迭代次数和最优求解效果。若以最大迭代次数为停止条件，则算法在运行达到设定的最大代数后，停止运行。若以最优求解效果为停止条件，则算法运行求得的解达到设定该问题的初值时，停止运行。

1.2 层次分析法

层次分析法(Analytic hierarchy process，简称AHP)由美国运筹学家A.L.Saaty于20世纪70年代提出。它是以一个复杂的多目标决策问题为系统，将此系统进行分解，成为多指标(或准则、约束)的若干层次目标或准则，从而量化算出层次单排序(权重)和总排序，以此来优化决策方案[3-5]。

层次分析法的主要包括以下步骤：

步骤1：建立层次结构模型。通过对多目标决策问题进行分析，使其分解为若干层次，根据各个层次和因素之间的关系建立层次结构模型。

步骤2：构造成对比较阵。以层次结构模型的第2层为基础开始，对于上一层每个要素的同一层因素，用成对比较法和1-9比较尺度构造成对比较阵。其中bij为元素bi与bj的重要程度，1-9标度含义如表1所示。

表1 1-9标度重要性含义

步骤3：计算权重系数。建立判断矩阵B后，计算各指标的相对权值。操作如下：

1)将判断矩阵按每一列作归一化处理，其元素的一般项为：

(4)

2)将每一列归一化处理后的判断矩阵按行相加，其一般项为：

(5)

3)对向量w=(w1,w2,…,wn)t归一化处理，得：

(6)

w=(w1,w2,…,wn)t即为所求特征向量，即为权向量。

4)计算矩阵最大特征根λmax。

(7)

得到后进行一致性检验，使用指标为一致性指标C.I.。

(8)

平均随机一致性指标为R.I.，其对应数值表如下：

矩阵阶数12345678910R.I.000.580.91.121.241.321.411.451.49

定义一致性比率C.R.

(9)

当C.R.=0时，K具有完全一致性；当C.R.<0.1时，K具有满意一致性；C.R.≥0.1时，认为判断矩阵不符合一致性要求，需要对该判断矩阵进行重新修正。

2 工程及安全评价模型求解

2.1 工程概况

临洪西泵站是一座大型泵站，其位于连云港市北面郊区10000m处301国道北面，对其工程安全的研究具有重大意义。临洪西泵站在乌龙河下游入临洪河口处，距入海口12km，对控制洪涝起着重要作用。临洪河位于连云港市市郊，与新沭河、乌龙河、鲁兰河、淮沭新河和菌薇河相连，汇集于临洪河涌入大海。

临洪西泵站这座大型泵站，在新沐河行洪扩大为7000m3/s后解决了沭南地区的洪涝灾害，对解决乌龙河流域范围内197km2的内涝也起到了重要作用。当新沭河发生几十年一遇典型性洪水、临洪河交汇处水位发生急剧变化，与此同时乌龙河流城也发生几年就出现的内涝的内涝，临洪西泵站可以体现其及时排涝的作用，确保农家几十万亩农田免遭洪涝灾害。

2.2 泵站安全综合评价基本信息

根据《临洪西粟站安全复核报告》可得泵站渗流表，站身整体稳定表、翼墙稳定表，分别见表2、表3和表4。

表2 泵站渗流表

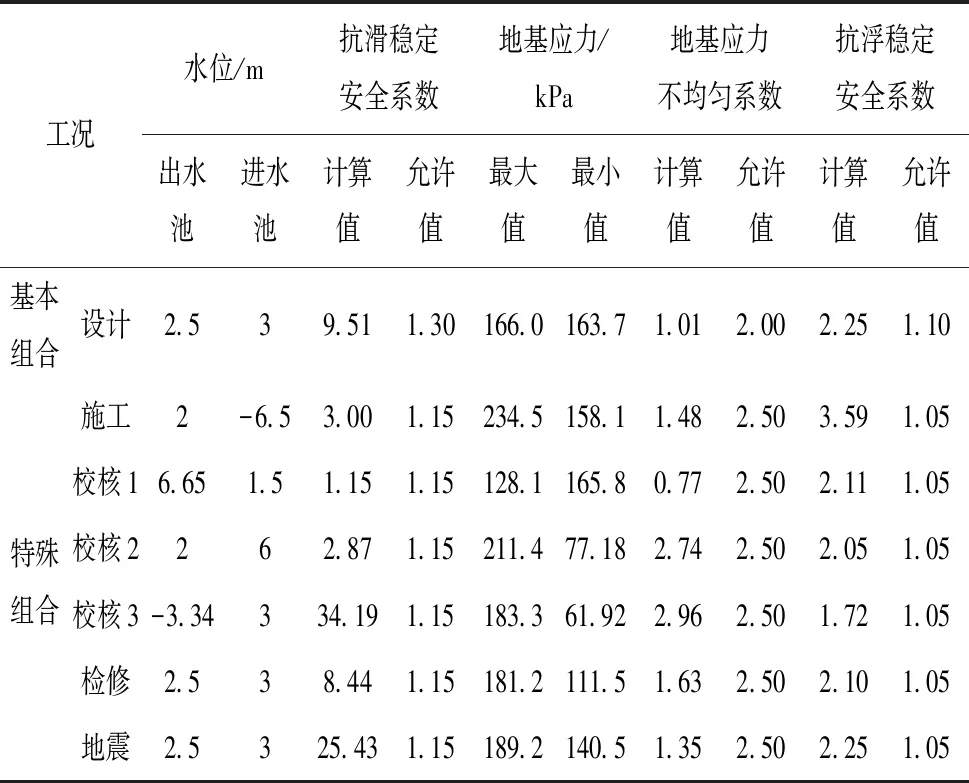
表3 泵站整体稳定表

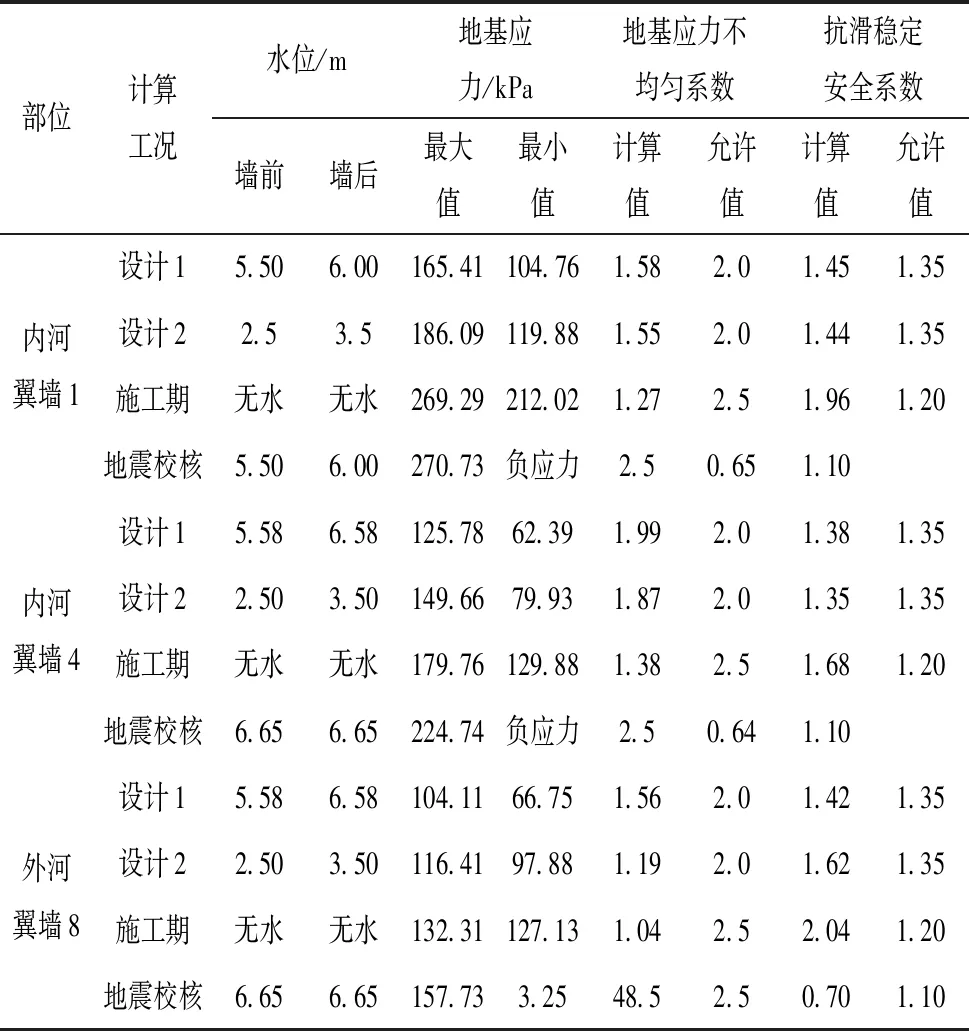
表4 翼墙整体稳定表

2.3 模型分析

现以泵站安全综合评价中安全状态这个分目标下的站身稳定一级指标为例，来确定抗滑稳定、地基应力、地基应力不均匀系数和抗浮稳定4个二级指标的单排序权重。泵站安全评价标准见表5。

表5 泵站安全评价标准

根据上表所示，设判断矩阵A为进水闸墩一级评价指标单样本权重，根据层次分析法计算得矩阵A的权重为{w(i,1)}={0.0494，0.1166,0.2618,0.5726}，该指标权重分别对应处于安全级别1、2、3和4级。

根据表5，可在安全、基本安全、较安全、不安全4个等级的每个评价标准变化区间中，任意产生4个安全评价指标值，为详细说明在各级评价标准的边界值，分别选取1次各指标的边界值，安全等级值为与该边界值相关的两个安全等级值的平均值。这样就构成了23个样本点组成的样本系列，如表6样本序号1-23所示。

表6 泵站安全评价样本集

显然，表6样本集中各指标值的大小与安全程度呈正相关，因此根据式(8)可计算相对隶属度值为{r(j,i)|j=1-23,i=1-4}，进而得到各指标值s(i)分别为0.317、0.316、0.315、0.311。相对重要性程度bm=1.019，由此可得安全评价指标1-4的样本集权重的判断矩阵B：

用层次分析法和遗传算法计算该排序权重，各权重的初始变化区间均取[0,1]，初始种群取300，得到上述评价指标的排序权重值为{w(i,2)}={0.2518,0.2510,0.2499,0.2473}，进而可得的一致性评价指标系数值为0.001，该值<0.1，说明该判断矩阵符合一致性评价。

根据泵站进水闸墩的四个二级评价指标安全值隶属的安全级别和评价指标种类代入式(5)归一化后，可得它们的组合权重为w={0.4288,0.1912,0.1907,0.1893}，从该结果可以看出抗滑稳定的权重值比其他3个的权重值大，说明该指标更加重要，而其他3个相差无几，说明重要性程度基本相同[6]。

3 结 论

本文研究分析了遗传算法在大型泵站工程安全综合评价中的应用，通过阐述了遗传算法和层次分析法的基本原理，研究了大型泵站的基本特点并提出了大型泵站安全综合评价的模型及方法。经过实例研究分析发现，基于遗传算法的研究模型与一般层次分析法相比，具有明显的优越性。基于遗传算法的研究模型只要求提供目标函数的数值信息，该模型求解算法求解精度高，计算结果稳定。