基于加权最小二乘的结构模态参数与损伤识别

徐 强，刘 博，陈健云，李 静，徐舒桐

（1. 大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024；2. 大连理工大学 工程抗震研究所，辽宁 大连 116024）

1 研究背景

强风和地震等灾害会对建筑物造成不同程度的损伤，导致结构力学性能发生改变，进而引起结构频率、阻尼等参数的改变［1-2］。精确地识别出结构模态参数对结构健康监测与损伤识别十分重要［3-5］。

近些年，通过结构振动数据进行系统辨识及损伤识别的研究较为广泛，研究方法主要包括最小二乘识别［6-8］、卡尔曼滤波［9-10］、小波分析［11-12］及基于人工智能的遗传算法［13］等。如罗钧等［7］提出了基于约束最小二乘的识别方法对剪切型框架结构的损伤进行定位和定量，但测试过程中存在的噪声对识别结果造成了一定影响；何浩祥等［9］提出基于静动力凝聚方法的扩展卡尔曼滤波对梁桥结构的模态进行识别，进而诊断结构的损伤程度；Pahlo 等［12］将单元模态应变能的小波系数差应用于简支梁的损伤识别中，根据小波变换系数的变化对结构进行损伤定位，但该方法需要建立精准的有限元模型。最小二乘辨识是实际工程中最为常见的一种参数识别方法，但系统的输入输出信息难免会存在噪声，且多为白噪声，其在整个频率上的功率谱相同，而输入输出信号在不同频段有不同的功率谱。即不同频段输入输出时程信息的信噪比不同，识别结果的可信度也不同［14］。而最小二乘方法对于各频段识别结果的权值是均等的，分频加权最小二乘在最小二乘方法的基础上进行改进。选择可信度高的频率段给予较大的权重，可信度低的给予较小的权重，提高了识别精度［15］。

本文采用切比雪夫滤波器将系统的输入和输出信息平均分解到不同频率段上，分别基于各频段能量和普通克里金插值法作为权重，提出分频段加权最小二乘识别法，利用一个五自由度数值模型验证参数识别的准确性。将上述识别方法应用于Koyna混凝土重力坝在地震作用下的线弹性和弹塑性损伤模型中，通过坝体观测点在不同时刻识别的模态参数，识别坝体的损伤的区域，并采用有限元数值模拟对识别结果进行验证。

2 分频段加权最小二乘法识别

2.1 最小二乘法识别地震荷载下单自由度系统动力方程为：

即

式中：m、c、k分别为结构的质量、阻尼和刚度；ag（t）为地震加速度时程；ξ、ωn分别为结构的阻尼比和固有角速度。

从式（2）可以看出，结构的振动情况是由阻尼比ξ和固有角速度的平方ω2n共同决定的。定义结构的单位质量刚度＜k＞=k/m，结构的单位质量阻尼＜c＞=2ξωn。

对于单自由度体系，应用最小二乘方法识别系统参数，相当求解以下方程组：

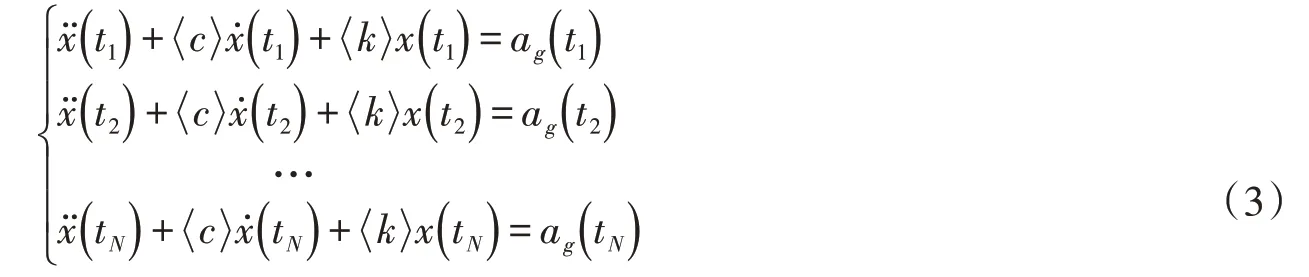
式（3）可以写成：

其中：

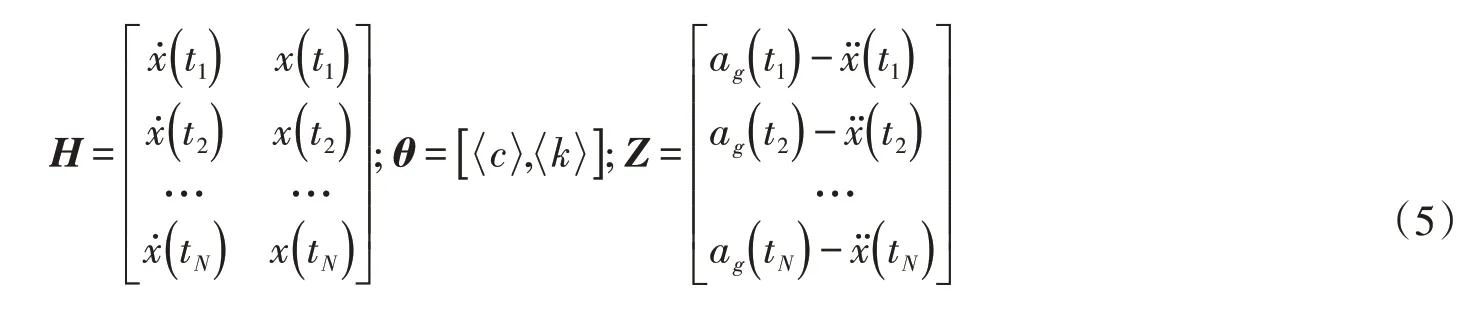
式中N为采样点数。

参数θ的最小二乘估计解为：

对于多自由度系统（如图1）：

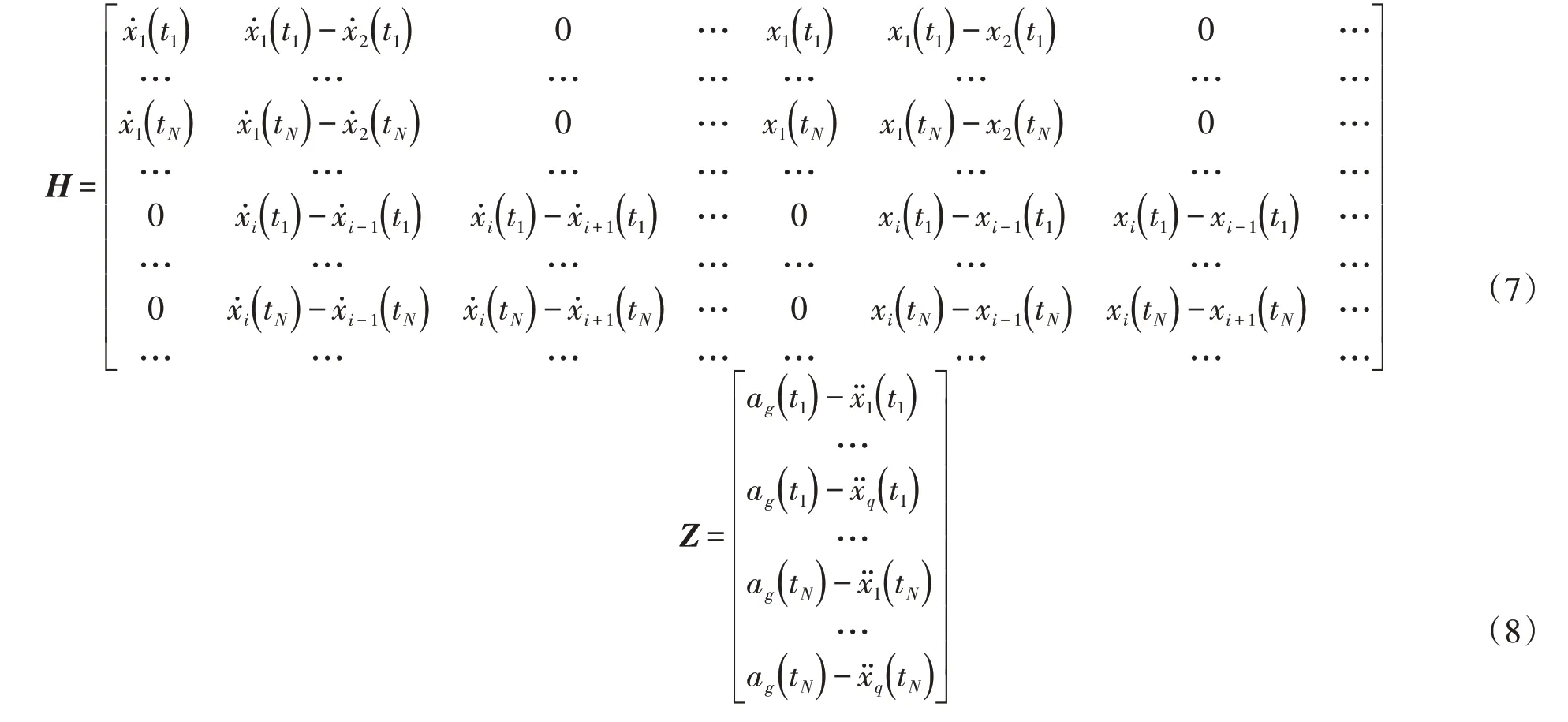
式中：q为多自由度系统节点个数；下标i代表第i个节点；ag(tN)为地震加速度时程；N为采样点数。

采用式（6）可识别多自由度系统的单位质量刚度＜ki＞和单位质量阻尼＜ci＞。

2.2 分频段方法本文采用切比雪夫带通滤波器将结构的输入输出信号根据频率的高低平均分成p个频段区间进行滤波，所得到的滤波后的每一个输入输出信号时程应用式（6）—式（9）计算多自由度系统的单位质量刚度＜ki＞j和单位质量阻尼＜ci＞j，j=1，…，p，下标j代表第j个频段区间。然后加权求和。

切比雪夫滤波器的幅度与频率的关系可用下式表示：

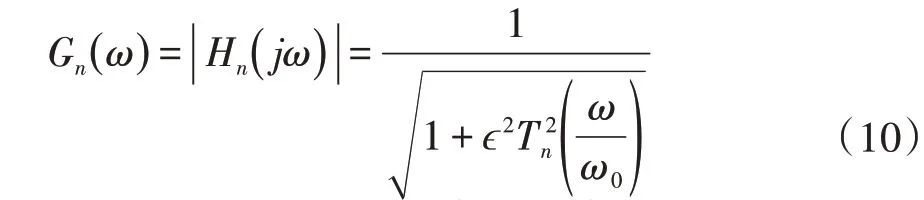
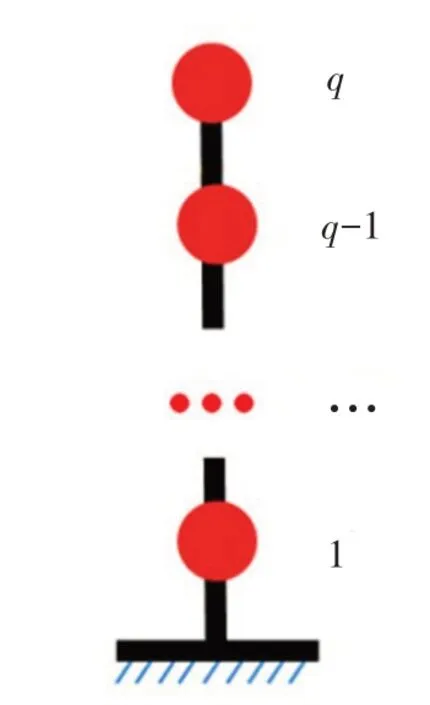
图1 多自由度系统

式中：ϵ为带通波动系数，为滤波器在截止频率ω0的放大率；为n阶切比雪夫多项式。

将以上低通滤波器进行如下变换可得到带通滤波器：

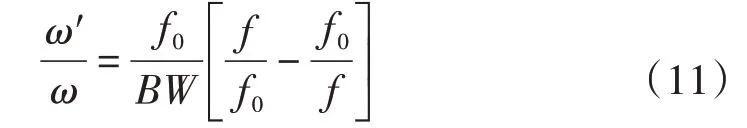
式中：f0为带通滤波器中心频率，分别为带通滤波器的上、下边界频率；BW为滤波器的带宽，BW=fh-fl。

2.3 加权方法（1）基于能量加权方法。取输入输出信号每个频段区间j滤波后的时程求方差和MDj（代表信号的能量），通过方差和求各个频率区间的权重λj：

式中：Xm,j为j频段第m个样本信号幅值；为j频段的平均幅值。

式中：θ̇为多自由度系统单位质量刚度＜ki＞和单位质量阻尼＜ci＞的估计值。

（2）基于普通克里金模型计算权重方法。普通克里金插值综合考虑了空间异质性及依赖性，在模型的模拟和预测方面取得了良好的体现［16-19］。定义无偏估计条件：

式中：E（·）为期望；θ0为估计值。

定义目标J：

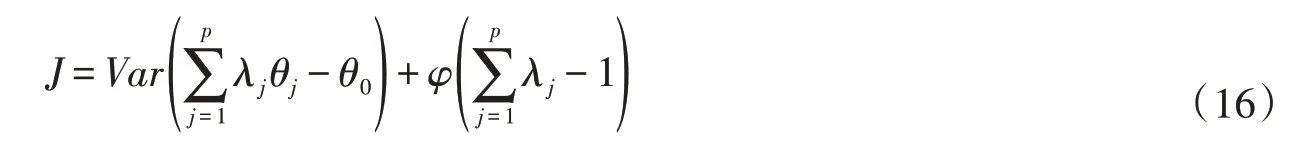
式中：Var（·）为方差；φ为拉格朗日乘数。

通过计算下式可求出各个频率区间的权重λj：

2.4 模态识别方法通过以上方法识别多自由度系统单位质量刚度＜ki＞和单位质量阻尼＜ci＞的估计值，从而得到系统单位质量阵、系统单位刚度阵和系统单位阻尼阵，进行模态计算识别。当阻尼比较小时，可直接对系统单位刚度阵＜K＞做特征值求解得到结构固有频率和振型。

3 数值算例

为了对本文的方法进行验证，设计一个五自由度剪切型框架结构，由于计算单位质量刚度，取节点质量为1 kg，阻尼为0.1 N/（s/m），刚度为100 N/m，在水平峰值加速度0.474g、竖直峰值加速度0.312g的Koyna 地震动作用下（如图2），通过有限元数值分析得到结构各节点的水平位移、速度及加速度响应。分别采用三种方法对结构的模态参数进行识别：（1）方法一。对系统输入输出信号进行最小二乘识别；（2）方法二。采用切比雪夫带通滤波器将结构的输入输出信号在1 ～100 Hz 的频率范围内平均分成5 个频率段，进行最小二乘参数识别，然后以各频率段的能量作为权值，进行加权计算；（3）方法三。基于普通克里金插值方法求出权值，对信号进行分频率段加权最小二乘辨识。将识别的结构一阶固有频率与有限元数值计算结果进行对比，如表1所示。

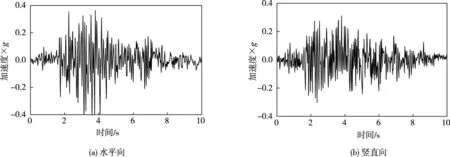
图2 Koyna地震波的加速时程

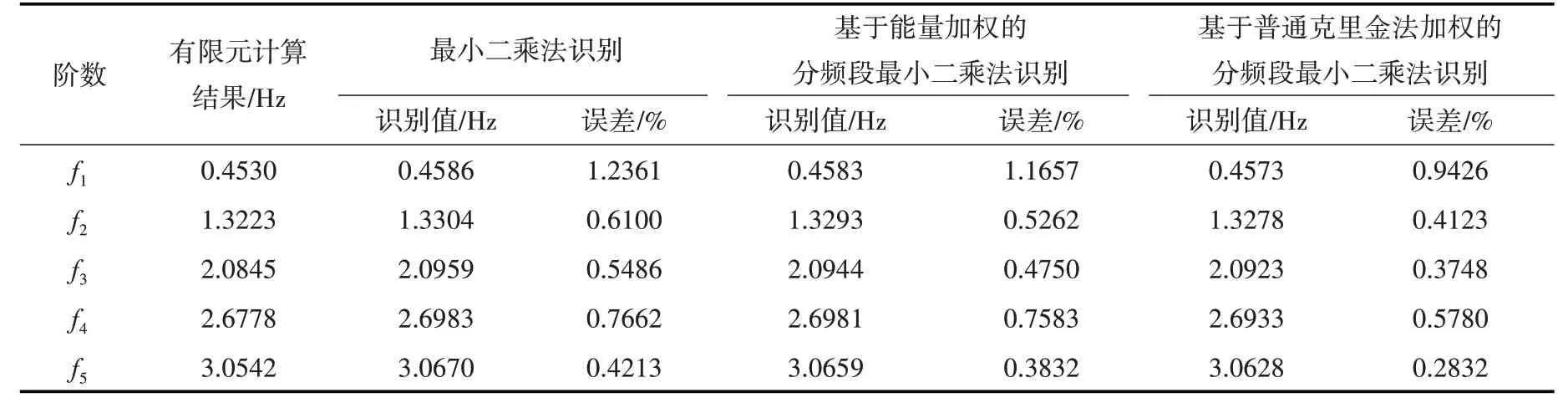
表1 固有频率识别结果

从表1可以看出，上述方法均可以准确地对结构的固有频率进行识别，在对输入和输出信号进行加权分频后，固有频率识别值的精确度有明显提高。其中基于普通克里金插值的分频段加权最小二乘的识别误差均在1%以内，最小误差为0.28%，即基于普通克里金加权的分频段最小二乘法对结构固有频率的识别效果最佳。

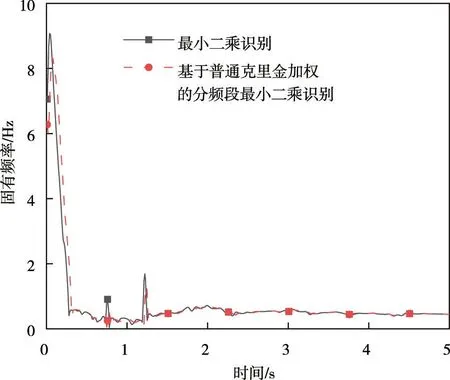
图3 一阶固有频率时程

为了能够将此方法用于识别时变系统，对不同时刻的模态参数识别情况进行描述，将时间段0.5 s内的50个数据点作为识别点，即采用本文提出的方法识别结构前9.5 s的一阶固有频率时程。通过最小二乘识别和基于普通克里金加权最小二乘识别的结构前5 s 固有频率时程曲线如图3 所示。从图3可以看出，对信号进行分频加权后，固有频率时程曲线更加平稳，连续性更好。在0 ～3 s 时由于地震波处于上升段，幅值非平稳较大，固有频率的识别值波动较大，与理论值有较大的差距，3 s后识别值逐渐趋于稳定，且最后识别结果与有限元计算结果较为相近。

将结构的输入、输出信号平均分成8个频率区间，分别采用上文的三种方法对结构的固有频率进行识别，得到的结果如表2 所示。表2 与表1 对比可知，在增加信号的频率区间后，分频加权最小二乘方法的识别精度有明显的提高。

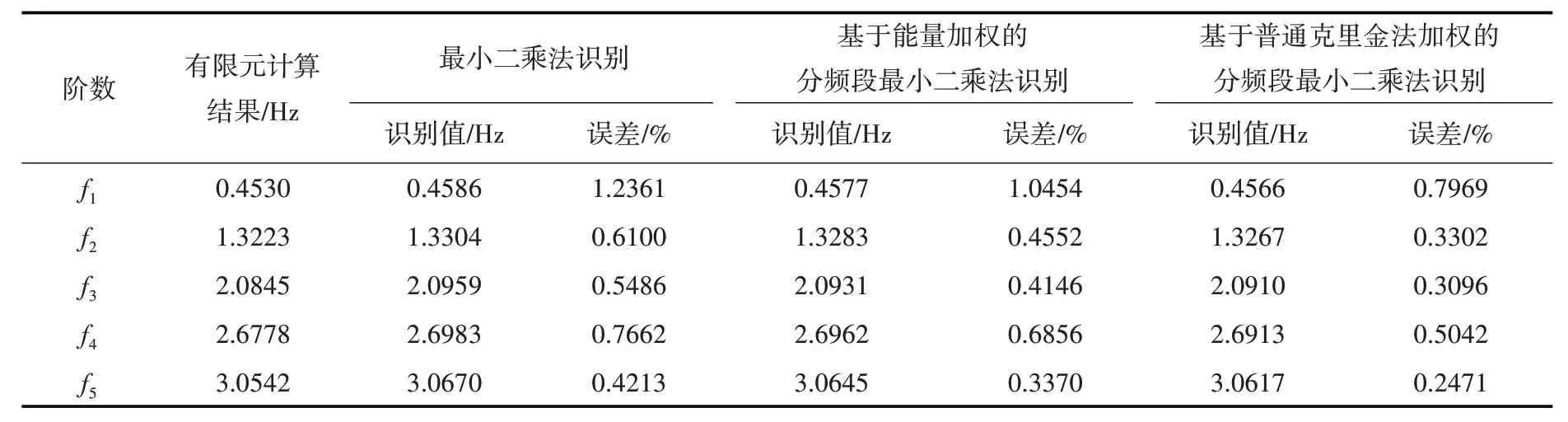
表2 八阶频率区间的固有频率识别结果

4 实例分析

4.1 Koyna 混凝土重力坝结构模态参数识别Koyna 混凝土重力坝是强震作用下发生破坏的实例之一，被很多学者用于结构的动力响应分析以及结构抗震性能评价［20-22］。坝体高度为103.0 m，坝顶和坝底的宽度分别为14.8 m 和70 m。本构模型采用混凝土线弹性模型，混凝土弹性模量为31 GPa，泊松比为0.2，密度为2643 kg/m3，有限元模型如图4所示。计算荷载为重力和地震荷载。在坝体上游面取5 个监测点，高程分别为：9.267、31.06、45.6、76.5 和103 m，通过有限元数值模拟计算出其在Koyna地震作用下的水平和竖直位移、速度及加速度响应，并将响应信号分别代入到模态识别的三种方法中，得到识别的结构模态参数。将结构水平向响应作为输出信号所识别的坝体五阶固有频率，与有限元模态分析计算的坝体十阶固有频率进行对比，发现所识别的五阶固有频率与有限元模态分析的第一阶、第二阶、第三阶、第五阶和第八阶频率存在着对应关系，结果如表3所示。从表3可以看出，采用分频段加权最小二乘识别方法，对结构固有频率的识别误差明显小于最小二乘识别。其中基于普通克里金加权的分频段最小二乘的识别精确度最高，这一结果也与第3节的数值验证的结果相一致。分频段加权最小二乘识别对结构第二阶和第五阶固有频率的识别误差相对较大，其他阶固有频率的识别误差均在3%以内。以上分析说明，基于普通克里金法加权的分频段最小二乘识别可以更为准确地识别结构的固有频率。

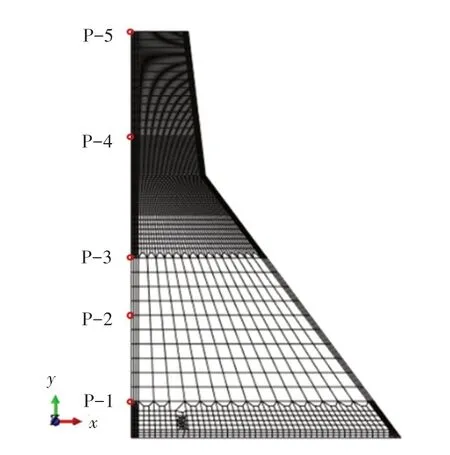
图4 Koyna重力坝有限元模型

4.2 Koyna 重力坝在地震响应下的损伤区域辨识结构发生损伤会导致刚度和模态发生变化，已有学者将其应用于结构的损伤定位［3］。本文采用分频加权最小二乘方法分别对结构的刚度和模态进行识别，得出其对于模态的识别效果要优于刚度，因此基于其对固有频率和振型的识别结果对结构的损伤进行描述。

Koyna 重力坝混凝土本构模型采用混凝土塑性损伤模型，其密度、弹性模量及泊松比与4.1 节中线弹性模型相同，膨胀角为36.31°，阻尼比为0.05，初始抗压强度和抗拉强度分别为24.1 MPa和2.9 MPa，有限元模型如图4 所示。计算荷载为重力和地震荷载。在坝体的上游面取与4.1 中线弹性模型相同的监测点，将坝体在垂直方向分成5 个区域，计算各观测点在Koyna 地震作用下的位移、速度及加速度响应信号，通过基于普通克里金加权的分频最小二乘方法识别结构的模态参数。

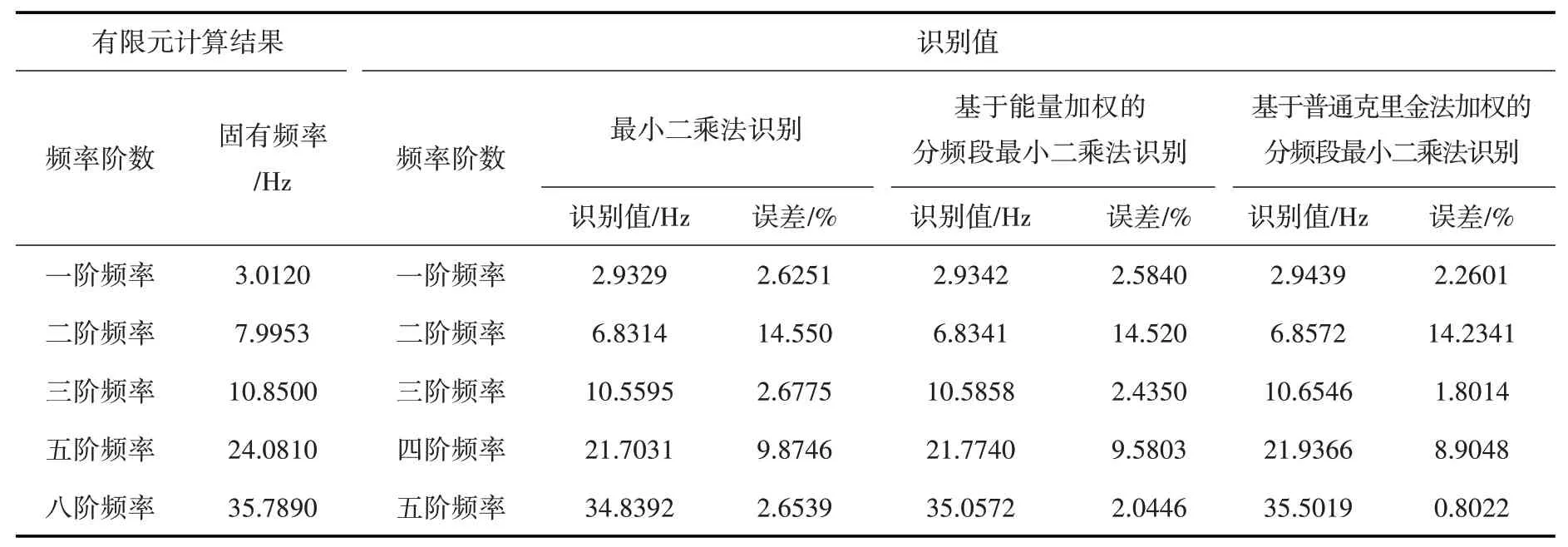
表3 固有频率识别对比结果

为了能够将此方法用于时变系统，从而描述坝体的损伤情况，将监测点在时间段0.5 s内的50 个时程数据点作为识别数据，将识别的坝体前9.5 s 一阶固有频率时程曲线与有限元计算的损伤分布对比，如图5 所示。从图5 可以看出，固有频率时程曲线在0.03 s 出现了下降趋势，通过有限元计算结果可知在0.03 s时坝体后折坡处开始出现损伤区域；在3.3 s时，时程曲线出现了较大幅度的下降，对比有限元损伤分布可知在3.3 s 后，坝体在后折坡处的裂缝沿水平方向急速扩展；在5.7 s 时程曲线不再下降，对比有限元损伤分布可知此时坝体几乎形成了贯穿的主裂缝区；在7.2 s 后出现了较大幅度的震荡，此时坝体已形成了贯穿的裂缝，裂缝上方的结构为自由振动状态，因此固有频率识别值波动较大。通过上述分析可以得出：基于坝体水平方向响应信号所识别的结构一阶固有频率时程曲线，可以较好的对其损伤发展进行描述。

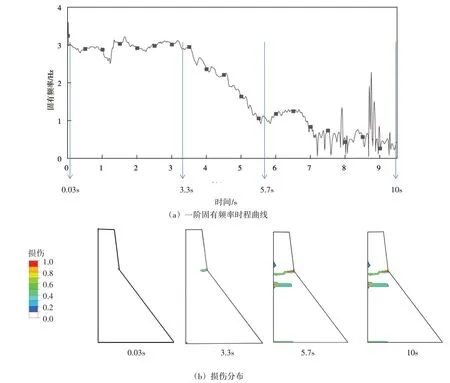
图5 一阶固有频率时程与损伤分布的对应关系

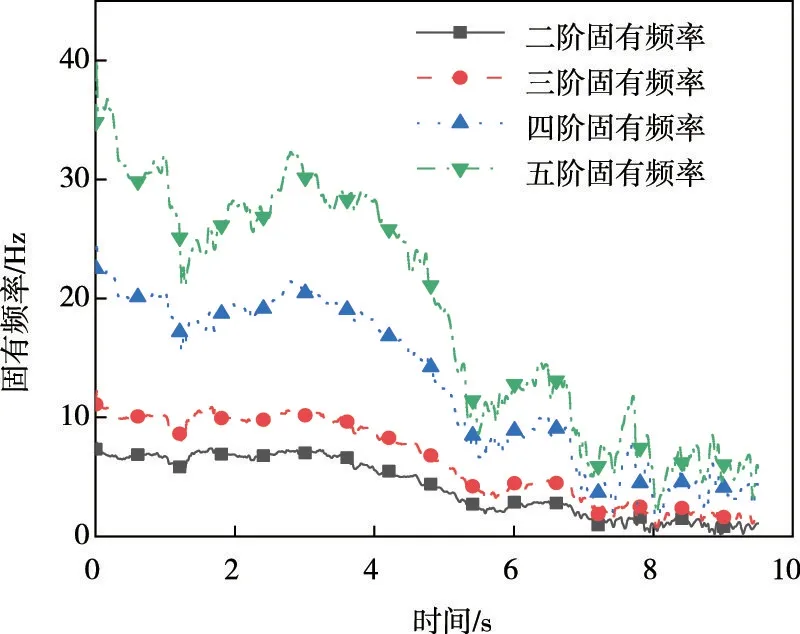
图6 水平向响应识别的二阶至五阶固有频率时程

重复上文步骤，得到结构二至五阶固有频率时程如图6 所示。对比图6 与图5 可以看出，二阶至五阶固有频率时程和一阶固有频率时程具有相近的变化规律，并且固有频率的阶数越高，曲线在损伤区域的下降幅度越大，形成贯穿裂缝后曲线的波动幅度也越大。

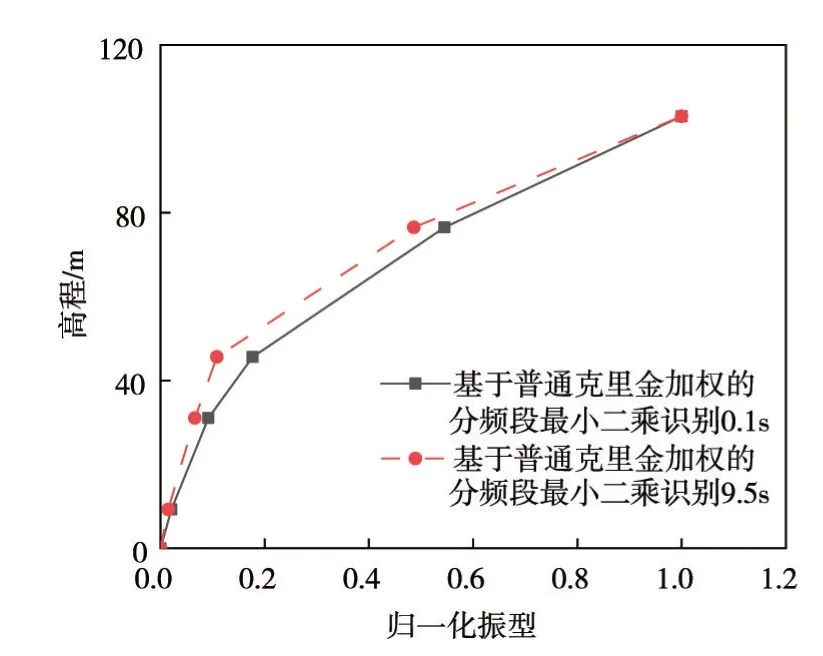
图7 塑性损伤模型上游水平向归一化振型

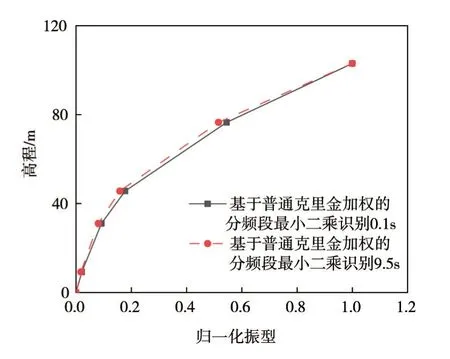
图8 线弹性模型上游水平向归一化振型

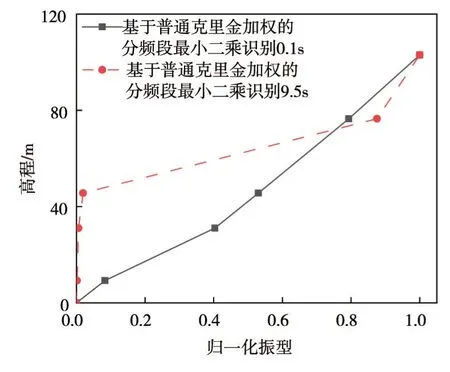
图9 塑性损伤模型下游向归一化振型

图10 线弹性模型下游向归一化振型

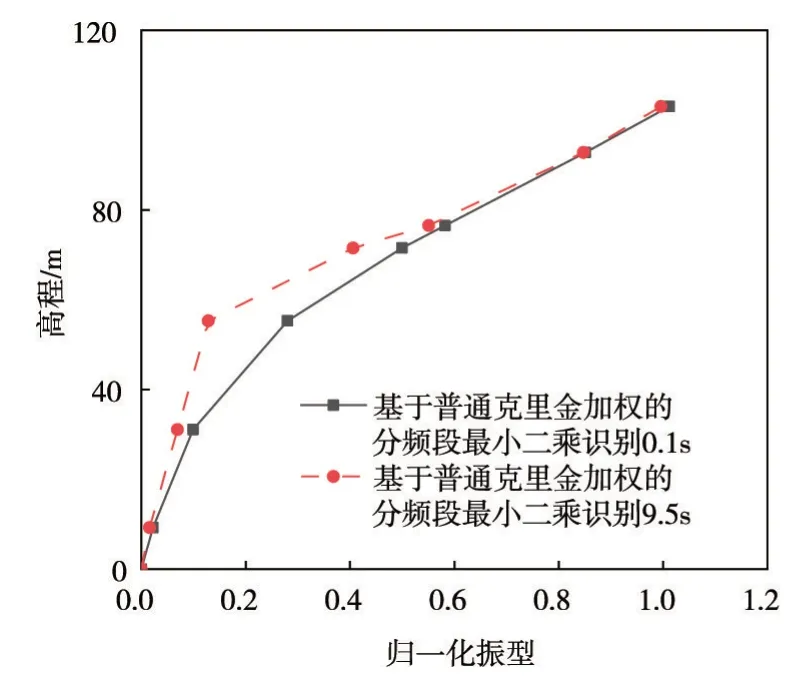
图11 塑性损伤模型7观测点上游向归一化振型

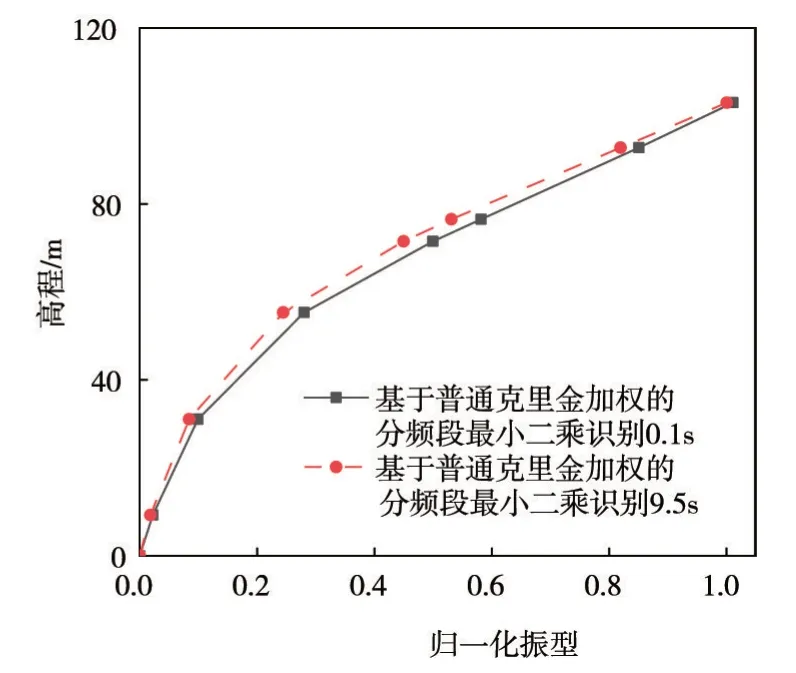
图12 线弹性模型7观测点上游向归一化振型

分别以监测点在初始时刻与9.5 s 时的水平响应作为输出信号，采用基于普通克里金加权的分频段最小二乘方法识别结构的一阶归一化振型，并对其取绝对值，如图7 所示。对4.1 节中的Koyna 重力坝线弹性模型进行相同的振型识别，结果如图8 所示。通过图5 中的坝体损伤分布图可知，坝体主要损伤区域为45.6 ～76.5 m 的坝体后折坡处，从图7 中可以看出，9.5 s 后识别的结构一阶振型在高程为45.6 和76.5 m 处出现了明显的拐点，这是由此时坝体后折坡处出现了贯穿的裂缝，其上、下两个监测点的响应信号发生变化，导致识别的结构一阶振型发生改变。而图8 中未发生损伤的线弹性模型则没有此变化，即根据坝体损伤前后归一化振型识别值的变化，可以识别坝体的损伤区域。

在与上游监测点同一水平线的坝体下游处，取对应的5个点作为下游的监测点，分别以Koyna混凝土重力坝弹塑性损伤模型与线弹性模型竖直方向响应作为输出信号，重复上文对结构在初始时刻和9.5 s 时的归一化振型识别，结果如图9 和图10 所示。从图9、图10 可以发现，采用下游观测点作为响应信号，同样可以根据坝体损伤前后归一化振型的变化确定其损伤区域。对比图7 和图9 可看出，采用下游观测点的竖直方向响应信号作为系统的输出信号，得到的归一化振型在损伤区域的斜率变化更为明显。

在坝体上游面选取7 个监测点，其高程分别为9.267、31.06、55.3、71.5、76.5、92.8 和103 m。重复上文中基于普通克里金加权的分频段最小二乘方法对结构初始时刻和9.5 s的振型识别，图11为基于坝体塑性损伤模型的识别结果，图12 为基于坝体线弹性模型的识别结果。通过图11 可以看出，在9.5 s 后结构一阶振型在高程为55.3 和71.5 m 处出现了明显的拐点，即该区域为识别的结构损伤区域。而上文通过5个监测点所识别的损伤区域在45.6 ～76.5 m 之间。说明适当的增加观测点，可以更为精准的通过振型变化识别结构的损伤区域。

5 结论

本文分别基于各频段能量和普通克里金插值作为权值，提出了分频段加权最小二乘对结构的模态参数及损伤区域进行识别。研究结果表明，在对系统的输入输信号进行分频加权后，可以明显的提高其对结构固有频率识别的精确度，且基于普通克里金加权的分频段最小二乘法的识别效果最佳。以Koyna混凝土重力坝弹塑性损伤模型在地震作用下的响应信号为输出信号，通过基于普通克里金加权的分频段最小二乘法识别的结构固有频率时程曲线可以准确地对结构的损伤情况进行描述。根据坝体结构在损伤前后所识别的归一化阵型的改变，可以对结构的损伤区域进行识别，且以下游监测点竖直向响应信号作为输出信号的识别效果最佳。