基于多种混合模型的径流预测研究

梁 浩，黄生志，孟二浩，黄 强

（西安理工大学 西北旱区生态水利国家重点实验室，陕西 西安 710048）

1 研究背景

河川径流作为水循环的关键环节，对其进行准确预报十分重要［1］。当前水资源系统受到诸多因素的影响，径流序列表现出多时间尺度变化特性和非平稳特性，这给径流序列的预测带来了难度。尤其是在极端天气频发的背景下，径流序列呈现更大的波动性［2］。当前，径流预测模型已有不少，从不同的模型中优选可靠的径流预报模型，获得更高的径流预测精度，是水文预报工作者迫切开展的工作。

为了获得未来几天、几个月甚至几年的径流预测值，水文预报人员已经提出了多种方法。这些水文预报模型方法可以大致分为过程驱动和数据驱动两大块［3］。过程驱动的模型以基于物理过程的水文模型为主，如王中跟等［4］通过SWAT模型利用地理信息系统和遥感的数据模拟流域上复杂的水文过程。数据驱动则主要通过针对水文站、气象站等观测的数据，结合统计方法进行径流模拟预测，如运用广泛的多元线性回归（MLR）［5-6］、人工神经网络模型（ANN）［7-8］和支持向量机模型（SVM）［9-10］等诸多基于人工智能的模型［11］。水文模型要涉及较为复杂的水文过程，需要大量准确的水文过程资料，需要考虑不同时空尺度下水文系统规律的差异性，存在参数不确定性以及水文模型普适性较差等问题［12］。数据驱动模型不需要考虑水文过程的物理机制，对时间序列进行数学分析，在解决数据预测问题以及时间序列分析等方面有独特的优势［13-14］。模型对不同数据有其适用性，本文首先优选多元线性回归、人工神经网络和支持向量机3种数据驱动模型中对渭河流域径流序列适用性最强的单一模型。

径流过程本身具有一定的周期性、趋势性以及随机性特征，给径流预测带来难度，所以径流的多时间尺度分析和认识对提高径流预测精度十分必要。分解技术可以将径流序列分解为一系列相对稳定的子序列。近年来研究者基于分解技术进行的径流预测研究已经有很多，对径流进行分解重构，最终实现径流预测的方法不断被应用，有经验模态分解法（EMD）、集合经验模态分解法（EEMD）和小波分解（WD）等方法。张洪波等［15］探究了对EMD 分解预测后的分量采用不同的重构方式及对于径流预报精度的影响。Tan 等［16］和杜懿等［17］采用EEMD 对径流进行分解，更好地得到径流的有用信息，提高预测精度。Mohammad 等［18］将EEMD 应用于韩国和伊朗河流的模拟预测，也验证了其良好性能。周婷等［19］探讨了基于小波分解的SVM 径流模拟预测，径流预测精度得到了提高。以上研究表明了基于分解技术的径流研究对径流预测精度的提高是有效的。然而，大多数研究者聚焦于采用单一分解方法的混合模型进行径流预测研究，缺乏对基于多种分解方法的混合模型进行综合对比分析及其适应性研究。

以径流时间序列为研究对象的数据驱动型径流预测模型，一般情况下模型的输入项为降雨等气象因子，同时考虑历史的径流序列。以输入因子为依据的预测模型可以大致分为3类：基于气象因素的径流预测模型；基于历史径流序列以及气象因素的径流预测模型；仅考虑历史径流序列的径流预测模型。白云天等［20］在对尼尔基水库的入库径流预报时选取的预报因子为前期径流以及降水。变化环境下水文序列发生了改变，给径流预测研究带来了困难。为得到较高的径流预测精度，丰富输入因子也是关键途径之一。孟二浩等［21］在径流预测时丰富了预报因子，加入北大西洋年代际震荡、北极震荡等因子对径流预测精度提高起到了作用。杨开斌等［22］探究了在汛期时ENSO 事件对于径流预测的影响。相关的研究表明大气环流异常因子对径流具有一定影响。值得一提的是，当前的研究主要集中于大气环流异常因子对于径流整体序列的影响，而没有考虑分解技术下大气环流异常因子对径流子序列的影响。

基于此，本文对比分析了基于EMD、EEMD和WD方法构建的多种混合模型进行径流预报的精度和效果，并融合大气环流异常因子的信息，以期揭示不同混合模型对河川径流的预测能力，为变化环境下径流预报精度的提高提供新思路。

2 单一预测模型

2.1 多元线性回归多元线性回归（MLR）是用于拟合多个自变量和因变量之间的线性关系，通过训练确定得出模型需要的参数，从而确定具体的MLR 方程，之后便可通过此方程来预测因变量［23］。其一般形式为：

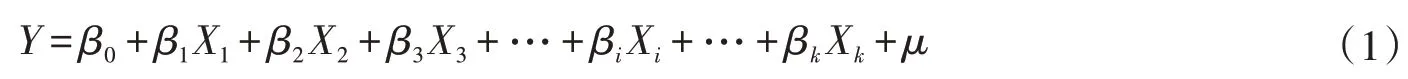
式中：Y为因变量；βi为回归系数，i=0,1,…,k；Xi为自变量，i=1,2,…,k；μ为随机误差项，。回归系数β的求解采用最小二乘法，使误差项的平方和最小。

2.2 人工神经网络人工神经网络（ANN）是一种通过模仿动物大脑神经的行为特征，从而进行大规模分布式并行信息处理的数学模型。ANN 由3部分组成：输入项、包含激励函数的隐含层和输出项。其依据的主要思想是：通过对输入输出数据的训练，建立能够以任意精度逼近最佳输出的非线性函数的模型［24］。

ANN以神经元作为基本处理单元。简单的ANN是多输入一输出的，其表达式为：

式中：Ii为隐含层的值；yi为输出值；xj(j=1,2,…,n) 为不同的输入信号；θi为阈值；wji为从神经元j到神经元i的权值；f（·）为传递函数。

ANN 通过不断地调整权值和阈值的大小，从而形成一种由输入到隐含层的固有模式，然后通过传递函数由隐含层到输出层。合理选择隐含层数和神经元个数对ANN十分重要。

2.3 支持向量机支持向量机（SVM）通过引入核函数，将原低维空间中非线性不可分的数据映射到高维特征空间。将两类数据分类问题转换为在高维特征空间中求最优的线性分类面，即找到的分类平面与最靠近的数据点之间距离最大［25］。SVM 进行模拟预测主要思路：通过训练期对输入输出数据的训练，建立结构风险最小化的模型，然后给定输入数据就可以得到相应的输出值。通用的SVM 表达式如下：

式中：xi为输入值；yi为与xi对应的输出值；sgn（·）为符号函数；为核函数；为调控SVM确定最优分类平面的参数。

核函数的选取是SVM 应用的关键之处。常用的核函数有：线性核函数、多项式核函数以及径向基核函数等。核函数计算公式如下：

式中ϕ函数将数据从低维空间映射到高维特征空间。

SVM 用于回归分析，能够对训练数据进行学习，并实现其余数据的模拟预测，很好的解决了非线性拟合问题。对于样本数据，xi、yi分别为输入变量和预测变量，n为数据量［26］。其回归函数为：

式中：φ(x) 为输入空间到高维空间的非线性映射；ω为权值向量；b为偏差。

SVM 基于结构风险最小化原理，而不是经验风险最小化，提高了模型的泛化能力，求得风险最小的f(x)：

式中：ε为损失系数；ξi、为松弛变量；C为惩罚因子。

3 分解技术

3.1 经验模态分解经验模态分解（EMD）简言之就是将一段时间序列依据指定的条件分解为多个本征模态分量和一个趋势项，使得每个本征模态分量的极值点和过零点数相等或者最多相差1，且相对于局部零值点是对称的［27］。其具体步骤如下：

（1）输入需要处理的原始时间序列y(t) ；

（2）找出序列中所有的极大值点和极小值点，根据三次样条函数分别拟合出上包络线yp(t)和下包络线并求出上下包络线的均值序列(t) 。计算公式如下：

（4）计算剩余项z1(t)，以z1(t)作为原始序列，重复第（2）和第（3）步。如果最后的剩余项zi(t)满足单调函数或至多具有一个局部极值点，此时zi(t)=q(t)为趋势项，完成整个分解。否则继续进行第（1）—（3）步。

式中r'i(t)为满足本征模态分量条件的序列。

EMD分解原始序列y(t)得到n个本征模态分量和趋势项。可表示为：

式中：ri(t)为原始时间序列的本征模态分量，i=1,2,…,n；q(t)为原始时间序列的趋势项。

3.2 集合经验模态分解集合经验模态分解（EEMD）与EMD 的目的是相同的，将原有的时间序列分解得到若干不同尺度的本征模态分量IMF 以及一个趋势项。Huang 等［28］发现EMD 分解得到的某些本征模态分量IMF 包含了不止一个尺度下的信号，有些信号出现在不同的IMF 中。通过加入白噪音改进EMD 得到的EEMD 解决了模态混叠的问题，能够更精确的分解得到不同尺度的本征模态分量和趋势项。EEMD分解时间序列的步骤如下：

（1）输入需要处理的原始时间序列y(t)；

（2）产生m组白噪声序列nj(t) (j=1,2,…,m)，要求m组白噪声的均值为零。分别加入原始序列中，序列变为zj(t)：

（3）对zj(t)进行EMD分解，得到n个本征模态分量rij(t)以及趋势项qj(t)：

（4）由第（3）步可以得到m组n个本征模态分量以及n个趋势项，求各项均值为序列分解的最终分量；

可以看出，EEMD同样将时间序列y(t)分为了若干的本征模态分量和趋势项。公式如下：

式中：r'i(t)为原始时间序列的若干本征模态分量；q'(t)为原始时间序列的趋势项。

3.3 小波分解小波分析（WD）是一种对时间序列在时域和频域上进行逐级分析的方法［29］。小波是均值为0，长度有限的波形。满足如下条件的函数为小波母函数：

其中：ψ(ω)为小波母函数；ψ(t)为在频率ω处的Fourier变换；ψ*(ω)为ψ(ω)的共轭函数。

小波变换是在时间和频率两域对信号的局部特征进行表征。在R上平方可积函数构成的函数空间L2(R)，f(t)∈L2(R)。则关于母小波函数ψ的连续小波变换公式为：

对于离散的信号，有离散小波变换，离散连续小波变换中的伸缩因子a和平移因子b得到，通常取。公式如下：

1989年，塔式算法融入小波变换中，实现信号的分解重构，即著名的Mallat 算法。分解和重构过程表达式为：

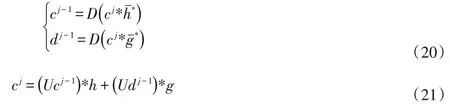
式中：cj为原始时间序列；h、g分别为低通、高通滤波器；cj-1、dj-1分别为分解尺度j-1下的低频信号与高频信号；分别为h、g的共轭反转；的卷积；为对卷积的二次下抽样；Ucj-1为对cj-1的二元上抽样；U、D为二元上、下抽样算子。

分解、重构后得到与原时间系列同长度的子序列，便于对时间序列进行预测。WD 方法应用于时间序列预测的步骤如下：（1）选择合理的小波函数，并选择合适的时间尺度（或小波分解水平）；（2）通过滤波器对时间序列进行分解，时间序列分解得到一个逼近信号序列和若干个细节信号序列；（3）利用小波重构方法可以得到与原序列长度相同子序列，最后进行时间序列模拟预测等工作。

结合以上模型方法，本文通过多站优选MLR、ANN、SVM 模型，选取最优的单一模型并基于此模型结合多种分解技术（EMD、EEMD、WD）构建混合预测模型，对比分析不同站点采用混合模型的径流预测精度高低；探究变化环境下丰富输入因子（大气环流异常因子）对于混合模型径流预测精度的影响。主要技术路线如图1所示。

4 实例应用

4.1 研究区域概况以渭河流域为研究区域，选取北道、林家村、华县3 个水文站作为研究对象。

图1 技术路线

其中，北道位于渭河上游，林家村位于渭河中游，华县站位于渭河下游。北道位于甘肃省内，地处秦岭北麓，集水面积1846 km2。渭河支流牛头河汇集汤浴河、后川河等诸多小河于天水市北道区注入渭河。林家村水文站位于陕西省宝鸡市，其集水面积30 661 km2，多年平均含沙量63.7 kg/m3，是渭河干流的控制站，属于国家重点水文站。华县站位于陕西省渭南市，集水面积106 498 km2，多年平均含沙量49.3 kg/m3，是国家重点水文站，同时也是渭河流域干流的控制站。渭河流域示意图如图2。

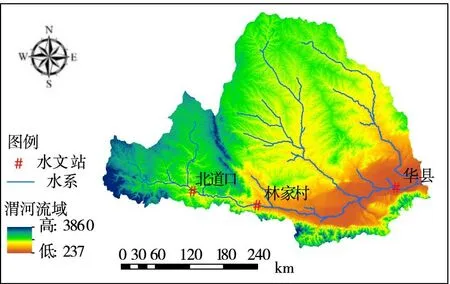
图2 渭河流域

采用的数据为北道、林家村、华县3 个水文站1960年1月至2010年12月径流，3 个水文站所在区域内相应时间的降雨、蒸发以及大气环流异常因子（北极涛动（Arctic Oscillation，AO）、太平洋十年涛动（Pacific Decadal Oscillation，PDO）、Nino3.4、太阳黑子）的月尺度数据。其中，以径流作为预测目标，以降雨、蒸发和前期的径流作为模型的输入项，将大气环流异常因子作为输入项增加项。

本文收集的4 种具有代表性的大气环流异常因子月尺度数据，其中，AO 数据从美国国家海洋和大气管理（National Oceanic and Atmospheric Administrator，NOAA）国家气象数据中心获取，网址为（http：//www.ncdc.noaa.gov/teleconnections/ao.php）；PDO 数据从东京气候中心获取，网址为（http：//ds.data/jma.go.jp/tcc/products/elnino/decadal/pdo.html）；Nino3.4 从NOAA 的地球系统研究实验室获得，网址为（http：//www.esrl.noaa.gov/psd/data/correlation/nina34.data）；太阳黑子数据从NOAA的国家地球物理数据中心获得，网址为（https：//www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/SUNSPOT/）。

由于降雨蒸发等因素对径流的影响存在滞后效应，不同因子对径流的影响时间存在差异，故本文基于相关系数对模型输入项进行优选。通过对于不同滞时下，各因子与目标因子的相关性计算，分析选取合理的因子，这对径流的预测是至关重要的。由于在径流预测中，考虑了滞时为一个月的径流作为预测下一月径流的输入项，所以径流预测的预见期为1个月。

4.2 径流序列突变分析以及时间尺度特性分析采用Mann-Kendall 变异诊断法对各研究站点径流序列进行趋势分析以及变异点诊断，结果如图3所示。

由图3（a）北道站的UF曲线可知：自1970年9月起北道站径流量有明显的减少趋势，且在1986年8月以后这种减少趋势超过了0.05的显著性水平，意味着北道站径流量下降趋势显著。同时可以看到北道站UF与UB曲线交点位于1988年1—4月，不在信度线之间，即径流量没有发生显著的突变。由图3（b）林家村站的UF曲线可知：自1963年11月起林家村站径流量有减少趋势，在1989年11月后减少趋势超过显著性水平0.05的临界线，并且自1992年10月开始趋势出现更明显的下降。林家村站UF与UB曲线交点位于1989年1月不在信度线之间，即径流量于此月发生突变，但交点已很接近信度线。由图3（c）华县站的UF曲线可知：自1963年11月起华县站径流量有减少趋势，在1980年7月至1984年11月之间有增加趋势，之后径流量为持续减少趋势且减少趋势超过显著性水平0.05的信度线。华县站UF与UB曲线交点位于1971年11月且交点位于信度线之间，即此月径流量发生由多到少的突变。

较长时期的河川径流变化受多种因素的影响，是气候变化和人类活动因素（如修建大量水利工程等）综合作用产生的结果［30］。渭河流域上的3个研究站点月径流序列均有趋势性变化，且华县站月径流序列发生了变异。渭河流域有大量灌区和水库水电站，主要灌区集中在关中平原，关中九大灌区依渭河横贯关中平原［31］。灌区灌溉用水量波动不大，且大多灌区建成时间较早。渭河流域的大中型水库修建时间为1960—1980年代［32］。理论上认为模型可以在训练期捕捉并学习到灌溉工程用水以及水库运行等人类活动信息。选取此3个研究站点，以期探究不同混合模型对变化环境下径流预测的效果及适用性，并且可以更真实的认识大气环流异常对于分解后径流子序列的影响。

图3 各站径流突变点检验UF、UB过程线

考虑滞后效应以及径流变化可能对模型效果的影响，故划分本文的训练期为1960年1月至2000年12月，验证期为2001年1月至2010年12月。在模型的训练期，模型将捕捉并学习到气候变化和人类活动因素的部分信息，并相应的体现在模型的参数变化上。在训练期实现对于模型参数的确定，验证期为预测验证样本进行径流预测［33］。在径流模型评价体系建立中，选取了纳什系数和均方根误差为衡量径流预测精度的评价指标。

4.3 选用MLR、ANN、SVM 模型进行径流预测本文基于相关系数选取合理的输入因子，分别计算北道、林家村、华县3个水文站径流、降雨、蒸发与径流的相关系数分析，结果如图4。

图4 基于相关系数的输入因子优选

基于相关系数优选输入因子（降雨、蒸发、前期的径流），相关系数大于0.3即满足95%置信度检验，满足置信度检验的序列作为预选输入项［25］。可以看出，华县站径流自滞时为1 时，相关系数大于0.3；降雨与径流的滞时为0、1、2、7、8个月的相关系数绝对值均大于0.3；蒸发与径流的滞时为1、2、3、7、8、9 个月的相关系数绝对值大于0.3。径流预报模型输入项需要高信息量，强相关性的因子。一些因子虽然与径流相关性好，但它们的作用是重复的。这样的因子并不能同其他因子配合共同对径流起作用，结果可能使预测精度降低，故需要剔除［34］。本文通过穷举法［35］获得最佳的输入项。如华县站的最佳输入因子有：滞时为1 的径流，滞时为0、1、2 个月的降雨以及滞时为1、2、3、7 个月的蒸发。同理优选得到北道站、林家村站的最佳输入因子，然后以输入因子、目标因子建立单一模型（MLR、ANN、SVM）。本文选用ANN 中的BP 三层神经网络，模型训练函数采用trainlm［36］。对于隐含层神经元个数，本文在训练过程预先选定一个较小的值，然后依次增加神经元数，取验证数据误差达到最小时的隐层神经元数为最终隐层单元数。由于径向基核函数具有稳定性和去记忆性，故SVM 模型构建中，对比选用了径向基核函数，不敏感损失系数ε取0.001，采用网格寻优方法确定惩罚因子C和核函数参数g［37］。在预测验证期，将相应滞时下的前期径流、降雨、蒸发作为输入项，输入已训练好的模型，可得到预测径流。基于不同单一模型的径流预测结果，如表1所示。

通过表1 可以得出，对于不同站点，采用MLR、ANN、SVM 模型预测径流精度有较大差距。林家村站体现尤为明显，采用MLR 模型验证期其纳什系数仅为0.150，均方根误差为0.733；采用ANN模型，验证期其纳什系数为0.332，均方根误差为0.642。据调查可知，林家村站上游有大型灌区水库，需要取水调水，人为因素对径流的影响很强，使得林家村站径流预测模型中，MLR 模型的泛化能力弱，相比采用描述线性关系的MLR 模型，采用模拟非线性关系的ANN 模型在处理径流及其影响因素之间复杂模糊的关系中更具有优势，泛化能力更强，预测时能得到更高的精度。采用SVM 模型预测林家村站径流，验证期其纳什系数为0.603，相较ANN 模拟结果提高了81.6%；相应的均方根误差为0.495，降低了22.9%，其模拟效果优于ANN的模拟效果，说明SVM相比ANN模型在预测径流过程中更具有优势。从模型原理探究原因，ANN 模型通过训练后建立了基于经验风险最小化的网络模型，存在着局部极小值以及具有不稳定性等缺点，而SVM 模型引用核函数，并且以结构风险最小化为原则，最终得到确定的唯一解，可以弥补ANN 的一些不足，所以模拟预测效果优于ANN。北道站以及华县站的径流预测结果分析亦可得到相同的结论。

表1 基于MLR、ANN和SVM模型的径流预测

4.4 基于混合模型的径流预测本文对北道、华县和林家村站的径流分别采用EMD、EEMD 和WD技术处理。EMD分解方法自适应的将北道站、华县站和林家村站分解得到的子序列个数分别为7、6、7。子序列分别包含各站径流的高频部分、低频部分以及趋势项。EEMD分解方法将北道站、华县站、林家村站分解后，得到子序列数分别为7、8、8。由于径流序列是离散的，所以采用离散小波分解径流。对于WD方法，小波函数以及分解层数的选择极为关键。通过对比优选，本文选取的小波函数为Daubechies小波系中的db3［38］，小波分解层数为5层，子序列有1个逼近信号（a5）和5个细节信号（d1、d2、d3、d4、d5）。

耦合不同分解方法与SVM 建立混合预测模型，即根据不同分解方法将径流序列分解为多个子序列；将各子序列分别建立预测模型进行单独模拟，最后将预测的各子序列值进行累加，从而得到最终的预测径流序列。以降雨、蒸发以及前期径流为输入因子，考虑各因子与各径流子序列的滞后性。对于各径流子序列进行模拟预测时，采用穷举法选取有效滞时下的影响因子作为模型的输入因子。将预测精度最高的径流子序列累加合成完整预测径流序列。同样，对于混合模型的预测径流精度通过纳什系数和均方根误差来评价。基于混合模型的径流预测结果见表2和图5。

通过表2基于混合模型的径流预测结果，可以看出不同研究站点的径流序列经过不同的方法分解后，子序列通过SVM 预测合成后的径流精度有明显差别。EEMD-SVM 分解预测的精度要普遍高于EMD-SVM 分解预测的精度。北道、华县、林家村径流预测精度提高幅度分别为21.6%、1.9%、4.8%。EEMD 方法改进了EMD 方法所存在的模态混杂问题，在时间序列分解上更有优势。WD-SVM分解预测的精度要高于EEMD-SVM 分解预测精度。但是不同站点区别很大，EEMD-SVM 模型在华县站径流预测中泛化能力较弱，采用WD-SVM模型进行分解预报相较EEMD-SVM 模型径流精度提高幅度为31.0%。而北道站，WD-SVM 与EEMD-SVM 径流预测精度相差很小。姜浩等［39］的研究发现：依据通量矩阵可得WD 方法在分解能力上优于EMD。由以上结果可知，不同径流序列对于分解方法有着不同的适应性，但一般来说预测精度高低符合如下表达式：WD-SVM＞EEMD-SVM＞EMD-SVM。

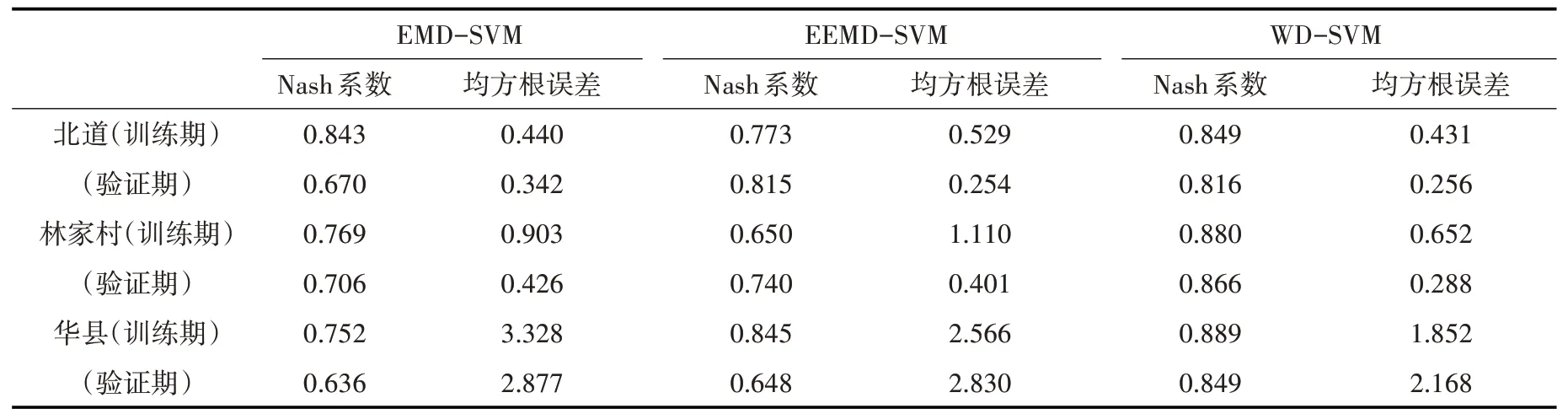
表2 基于混合模型的径流预测

施能［40］的研究表明大气环流是造成我国冬季气候变化的重要原因之一。本文研究区域为渭河流域，海陆热力的差异会给当地气候造成较大影响，同时可能会对当地径流产生影响。所以本文的输入因子在降雨、蒸发、前期径流的基础上，考虑大气环流异常因子（AO、PDO、Nino3.4、太阳黑子）作为径流预测的输入因子，并对增加大气环流异常因子前后径流预测精度进行了对比分析。原始径流采用WD 方法分解得到子序列，通过相关系数计算大气环流异常因子相对于各分解序列的滞时，优选大气环流异常因子作为输入项，采用SVM 模型进行预测。表3 为基于WD-SVM 混合模型的大气环流异常因子筛选结果。

如表3 所示，对于研究站点大气环流异常因子的筛选结果可知：4 个大气环流异常因子中，Nino3.4 对渭河径流影响明显，而AO、PDO 和太阳黑子的影响不明显；北道、林家村和华县站依次由西向东分布，季风对中国东部和中国西部的影响强度不同，且季风也会对Nino3.4 产生影响，故Nino3.4 对于不同水文站径流的影响会不同［41］；对北道站经小波分解后的径流子序列d3 进行预测时，增加滞时为3、4、5、8、9、10 的Nino3.4 作为模型输入项；累加分解预测后的径流子序列，径流精度得到了提高。针对小波分解后的各径流子序列通过支持向量机进行预测时，支持向量机中惩罚因子C和核函数参数g结果如表4所示。

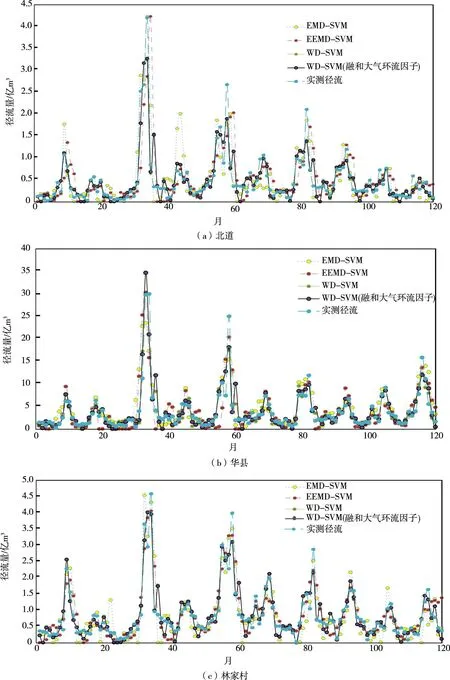
图5 基于分解的混合模型及融合大气环流异常因子的WD-SVM模型的径流预测

最终径流预测结果如表5 所示。验证期混合模型以及融合大气环流异常因子的WD-SVM 模型预测径流与实测径流对比情况见图5。

由表5 基于WD-SVM 模型丰富输入因子后的径流预测，可知相比输入因子只有降雨、径流以及前期径流，增加大气环流异常因子对3站的径流预测精度均有提高。北道站径流预测中纳什系数提高了0.25%，均方根误差降低了0.78%；林家村站纳什系数提高了0.23%，均方根误差降低了1.0%；华县站纳什系数提高了0.7%，均方根误差降低了16%。其次，对各研究站点径流极大值点（10 个左右）的预测精度进行了分析。WD-SVM 混合模型融入大气环流异常因子后，北道站其均方根误差减小0.9%；林家村站其均方根误差减小1.3%；华县站其均方根误差减小4.7%。结果印证基于分解技术下大气环流异常因子对于径流子序列有影响，丰富输入因子可以提高径流预测精度，尤其是对于径流极大值点的预测精度提高更为明显。

表3 基于WD-SVM混合模型的大气环流异常因子筛选结果

表4 基于小波分解的径流子序列支持向量机模型参数值

表5 基于WD-SVM混合模型融合大气环流异常因子前后的径流预测

综上所述，丰富输入因子后的WD-SVM 模型对研究站点的径流预测精度均高于80%。林家村站和华县站训练期以及验证期的径流预测精度不低于北道站（水利工程影响较小）。修建的大量水利工程并未对径流预测造成较大影响。其他学者也做了不少有关渭河流域径流模拟预测的研究，左德鹏等［42］基于SWAT 模型和SUFI-2 算法的研究结果中，林家村站和华县站月径流模拟结果为：林家村站校准期和验证期纳什系数为0.23 和0.75、华县站校准期和验证期纳什系数为0.72 和0.78；Zhao 等［43］基于分布式水文模型DTVGM 得到咸阳站（咸阳站位于渭河干流，林家村站和华县站之间）月模拟径流和观测径流纳什系数在0.6～0.7 之间；黎云云等［44］基于SWAT 模型的渭河流域径流模拟中，林家村站校准期和验证期纳什系数为0.58 和0.80、华县站校准期和验证期纳什系数为0.77 和0.82。而本文基于WD-SVM 混合模型径流预测结果中，林家村站校准期和验证期纳什系数0.880 和0.868、华县站校准期和验证期纳什系数为0.890 和0.855。通过单一预测模型和混合预测模型预测结果、以及与其他学者相关研究结果对比可知，基于分解技术来提高径流预测精度的有效性以及变化环境下融合大气环流异常因子会进一步提高径流预测精度。

5 结论

（1）本文采用MLR、ANN 和SVM 模型对渭河流域北道、林家村、华县站径流进行预测，结果表明，依次采用MLR、ANN、SVM 模型进行径流预测，预测精度不断提高。表明渭河流域上径流与其影响因素之间复杂的非线性关系占较大比重，在对径流预测过程中基于结构风险最小化的SVM 要优于基于经验风险最小化的ANN。

（2）混合模型的径流预测研究中，3 种混合模型的径流预测精度由高到低排序为：WD-SVM＞EEMD-SVM＞EMD-SVM。

（3）WD-SVM 混合模型中，预报因子加入大气环流异常因子，各站点的模型预测精度均得到了提高，尤其是对于径流极大值点的提升较为明显。最终，北道、林家村、华县站验证期径流的纳什系数分别为0.818、0.868和0.855。

（4）在对渭河流域不同站点径流预测研究中，相较于直接对径流序列预测，基于分解的混合模型预测精度更高。采用径流分解技术后可更好地呈现出径流的周期、趋势等本质特征，对提高径流预测精度起促进作用。在接下来的研究工作中，将有3个突破点：①大气环流异常因子对径流影响机理的深入研究，实现作为预报因子的有效辨别和预处理；②径流预测的模型进一步优化，提高其学习、泛化能力；③分解方法的优化，对径流序列进行更为本质的剖析，提高径流的预测精度。