基于分形理论的冰下水流流速垂线分布研究
罗红春,冀鸿兰,郜国明,张宝森,牟献友
(1. 内蒙古农业大学 水利与土木建筑工程学院,内蒙古 呼和浩特 010018;2. 黄河水利科学研究院,河南 郑州 450003)
1 研究背景
北方河流冰冻期常历时四个月之久,冰盖改变了河道水流结构,引起水流垂线流速重分布,这一特性已受到国内外河冰工作者广泛关注[1-3]。对冰下水流流速垂线分布的研究,较统一的认识可归纳为:稳封期固定冰盖条件下,受冰盖糙率及床面糙率综合增阻影响,水流流速减小;冰盖下最大流速位置较明流时下移,且随冰盖糙率改变而改变[4-6];冰下水流垂线流速不再服从明流时单一的指数或对数分布,而体现为冰盖和床面附近符合对数流速分布律[7]。研究表明,冰下水流流速事关输水工程冰期的输水能力与输水效率[8-9],因此,对冰下水流垂线流速分布的研究非常重要。目前,对封冻河道水流运动特性的研究,常采用Einstein[10]提出的阻力划分原则,以最大流速线为界,沿水深方向将水流分成两层等效明流流动层(冰盖区和床面区),并假定分层水流相互独立,分别只受冰底和床面糙率影响,分层水流流速均服从对数分布;陈永灿等[11]结合纵向流速沿垂向的双对数分布律,建立了全过流断面的流速分布;Larsen[12]利用冰盖流的原型观测资料,对流速分布曲线进行了描述,分析得出冰盖对水流流速分布的影响只限于靠近冰盖的上层,而靠近河床的下层流速则不受冰盖制约,验证了Einstein 假定的正确性;Lau 等[13]进一步研究发现,冰盖和床面糙率出现差异时,最大流速点会偏向光滑的一侧,二者糙率相等时,两层流速分布对称;Meyer[14]通过水流分区,给出了描述水流速度垂线分布的关系式,揭示了动床条件下冰下水流流动机理。
由于在工程应用中,水流流速分布多是基于方程求解得到的近似分布,对冰下水流,较为常见的是基于k-ε模型进行冰下水流流速分布研究[15-17],但分析过程相对复杂。因此,从标度指数出发,寻找流速分布规律成为水流流速研究的突破口,分形理论即为典型。分形(Fractal)最初由美籍法国数学家曼德尔布罗特(B.B.Mandelbrot)[18]于1970年代提出,用于描述自然界中具有自相似性、自仿射性的图形、结构及现象,如山脊线、海岸线等自然现象。分形理论现已在河流(网)的非线性动力系统防灾[19]等研究领域被广泛应用。
黄才安等[20]基于分形理论,对明渠水流流速及含沙量垂线分布的自相似性进行了研究,表明分形理论能推出明渠水流垂线流速分布和含沙量分布公式。由Einstein 的阻力划分原则及假定,冰盖下水流流速垂线分布可视为两层等效明流对数分布,类似于倪志辉等[21]提出的潮流中Ⅱ型垂线流速分布中的“C”型分布,研究结果表明,该Ⅱ型流速垂线分布同样存在变维分形现象。因此,对于冰盖下的水流垂线流速分布研究,不妨尝试在明渠研究的基础上,利用分形理论进行延伸,完善不同工况下水流垂线流速分布的研究成果。
河流弯道常常是封冻期引起卡冰结坝的位置,水内冰花形成及演变受制于水流速度场及温度场的分布[22],且低温水流状态下的泥沙具有较高的悬浮效率[23],泥沙重分布也会引起水流结构的调整,冰-水-沙-床-岸相互作用及变化过程与水流垂线流速分布直接相关。因此,分析冰盖条件下水流流速分布有助于理解冰凌生消、泥沙输移、河床演变过程及冰下输水能力,为工程实际提供设计、施工等理论依据,对防凌减灾工作具有一定的实际意义。
2 研究区域概况及方法
2.1 研究区概况什四份子弯道地处黄河内蒙古段下游(图1),位于呼和浩特市托克托县段,北纬40°17'39″,东经111°2'53″。河道呈上游西北急转为下游东南的“Ω”形走势,弯道曲率大,水流进出弯道方向约120°,河道比降约0.1%,河宽200 ~600 m。河道冰期多出现于11月下旬至翌年3月中下旬,持续百余天,多年(1998—2015年)平均流凌、封河及开河日期分别为11月22日、12月16日和3月17 日。封冻期,什四份子弯道两侧岸冰的生长,逐渐缩小河面宽度,同时有效输冰河宽在弯顶所在断面急剧缩小,严重降低水流的输冰能力,因此,该弯道常成为初始卡冰位置[24]。此外,在弯道卡口段(1—3 断面),河道横断面沿程束窄,加上垂向冰层的热力与水力增厚,明显降低了水流过流能力,引起冰下水流流速重分布。因此,了解弯道卡冰处的流速分布,将有助于研究弯道冰塞的分布及发展过程。
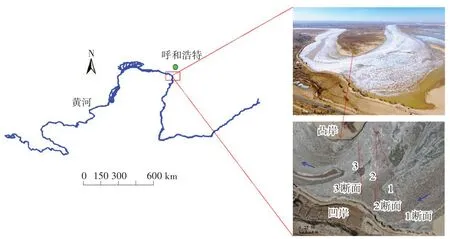
图1 什四份子弯道及断面分布
2.2 数据来源及方法冰封期(2019年1月10—13日)在什四份子弯道处进行钻孔测流,测流时间主要为下午3 点至5 点。基于ADCP 测流技术[25],采用钻冰机结合铁钎进行原位钻孔,通过下放ADCP潜入冰花层以下进行定点测量,流速测量采用延时采样,采样历时1 min、垂向采样间距10 cm,提取单孔测量数据,并按一定流速比尺进行表达,结果如图2,横线越长流速越大。为减小水流脉动影响,对采集的连续数据流进行平均,得到单孔有效水深下的垂线流速分布。试验共布设3 个断面(图1右下角彩图,顺水流方向依次为1断面、2断面、3断面),总计58个冰孔,各断面上每孔间隔20 m(近岸部分为10 m),其中测流共计34孔,未测流孔位用测深锤补充水深值。冰下水流流速因河型不同会出现一定的差异,为反映分形理论对不同河型的适用程度及水流垂线流速的分形现象,采用了头道拐水文站同期的水流垂线速度分布值(流速仪实测),该水文站位于什四份子弯道下游约5 km处,所处河道为顺直型。

图2 ADCP定点测流
基于分形理论,研究冰盖下水流流速垂线分布规律。分形原意是“不规则的,支离破碎的”,但体现了自然界某一类对象,其局部与局部/整体在形态和信息上具有自相似性的基本属性。自相似性可描述为标度不变性,即某一分形对象,其空间尺度r(或时间尺度t)倍乘λ后,其结构特征不变,只是在原来的基础上进行放大或缩小。标度不变性满足下式:

式中:λ为比例系数;α为标度指数;f(r)为某一物理量;f(λr)为f(r)乘以λ倍后对应的值。
式(1)也称为标度律,对尺度的选择可以是空间也可以是时间,当空间尺度r表征为长度时,标度指数α与分形维数D满足:α+D=1。其中,分形维数D是描述分形集几何特征的定量参数,可用来反映垂线流速分布的均匀程度,D值越大,垂线流速分布越均匀[26]。然而,对于同一河道断面的不同位置处,D值也可能不同。
分形标度律说明,尽管分形现象是复杂的,但是具有标度不变性,天然河道中的水流结构虽然复杂,但是对于明渠时的某一固定水深,沿水深方向整体水流垂线流速分布可看作是由对应某一水深处流速值的组合形式。垂线流速的分布特点体现了分形中局部与整体的自相似性,因此,该特点为分形理论在流速垂线分布的应用上奠定了基础。综上,运用自相似分形标度律的基础,重点在于空间尺度r(或时间尺度t)及物理量f(r)的遴选,且所选目标须具备自相似分形的特点。依托前人在明流条件下的工作基础,尝试基于分形理论研究冰下水流流速垂线分布,作为明渠水流研究成果的一个拓展。
3 结果分析
3.1 畅流期水流流速垂线分布依据黄才安等[20]的研究结果,明渠水流的流速垂线分布如图3(a)所示。显然,明渠条件下的水流流速分布具备分形特征,即通过放大图形OABO 一定倍数(λ)后得到的图形类似于OCDO,此时空间尺度r为长度y,对应物理量为流速u。因此,有:f(r)=u(y),λr=h=(h/y)y=λy,其中λ=h/y。由分形标度律可得:


图3 畅流期和冰封期水流流速垂线分布

式(4)即为明渠条件下水流流速垂线分布的指数形式,此时标度指数α=m,表示流速分布指数,说明基于分形理论能推得明渠水流的流速垂线分布公式。关于明渠水流垂线流速分布的研究已屡见不鲜[27-29],但总体而言,流速分布型式仍为常见的对数或指数型。
3.2 冰封期水流流速垂线分布冰下水流垂线流速分布如图3(b),一些学者的研究结果将其归结为抛物线分布[30]或双幂律分布[31]。采用Einstein 的划分方法,以最大流速线作为分界线,将冰-床双边界条件下的整个水流分成冰盖区(CEDC)和河床区(OEDO),则两个分区水流的流速垂线分布均近似呈指数或对数分布。
(1)在河床区(0≤y≤hm),由于冰盖区与河床区互不影响,水流垂线流速分布服从明渠水流的指数或对数分布。以指数分布为例,λr=hm=(hm/yb)yb=λyb,其中λ=hm/yb。流速分布即为:

式中:ub为距离河床yb处的流速;hm为最大流速点位置距离河床的高度;yb=y;αb=mb。
(2)在冰盖区(hm≤y≤h),以指数分布为例,则冰盖区流速分布与河床区流速分布镜像,即:

式中:ui为距离冰盖yi处的流速;yi=h-y;αi=mi。
以上分析结果表明,冰下分区水流流速垂线分布与明渠水流的流速垂线分布一致。
通过差异选取空间尺度,采用不同的比例系数和标度指数,基于明渠条件下不同学者的流速分布研究成果,可得到冰盖下不同形式的河床区和冰盖区流速垂线分布公式(表1、表2)。研究结果表明,利用分形理论能得到明渠水流的流速垂线分布公式,同时也能拓展到冰盖水流的研究中。
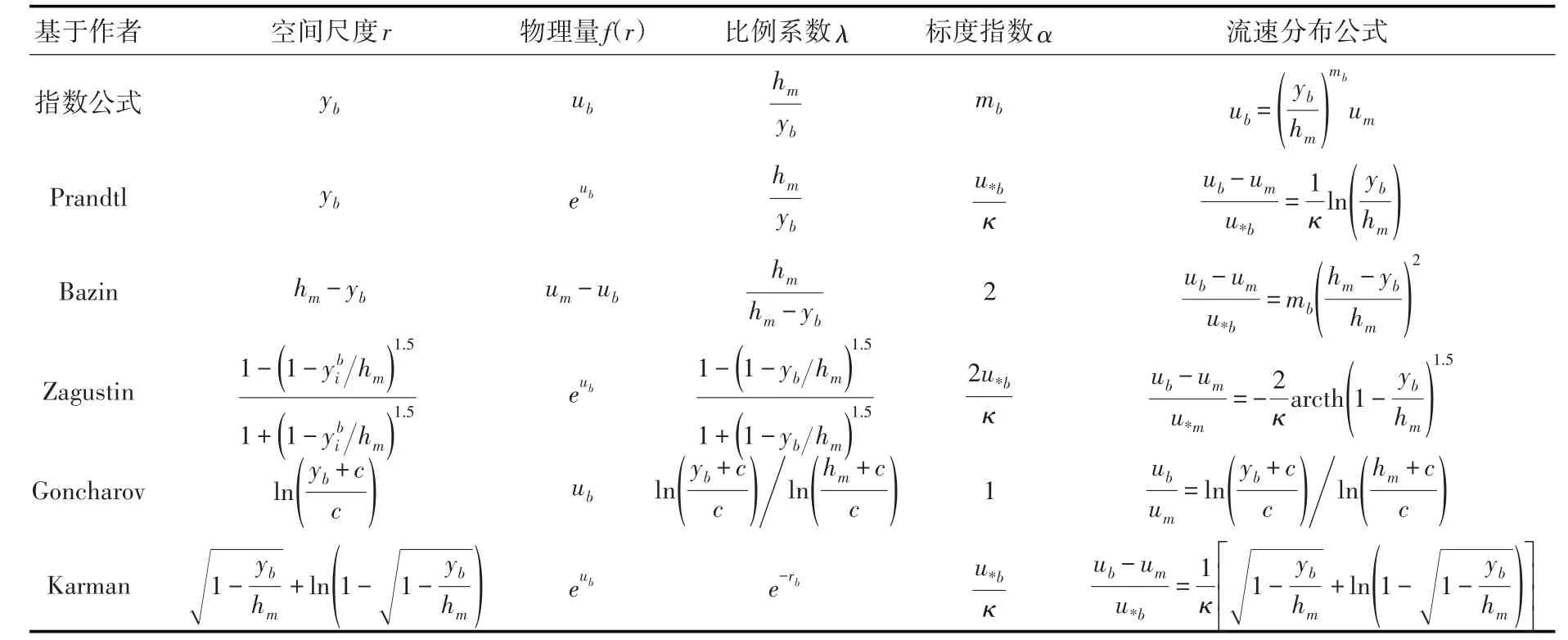
表1 由分形理论得到的各种形式冰盖下河床区流速分布公式

表2 由分形理论得到的各种形式冰盖下冰盖区流速分布公式
在研究水流流速垂线分布时,多采用基于Prandtl 假设的对数分布公式。对冰盖水流,由于双对数流速分布公式形式简单,具有一定的理论基础且准确性较高等特点,因此应用广泛。双对数流速分布公式(此处进行了统一)简记为:式中:河床区x=b;冰盖区x=i;ux为冰盖区或河床区的流速;yx为距离冰底或床面的高度;Kx为冰盖区或河床区的当量粗糙高度;u*x为冰盖区或河床区的摩阻流速;κ为卡门常数。

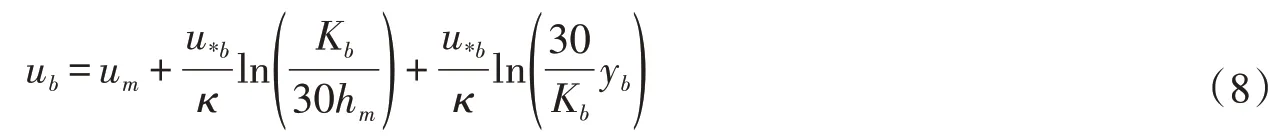
利用分形理论可容易推得冰下分区水流的流速对数分布公式,在公式的统一上,基于Odggard[32]对明渠水流的研究成果,Tsai[33]提出了冰下水流流速的双幂律分布公式,即:

式中:K0为给定流量下的常数;y为距离床面的高度;h为水深;α1为与流量阻力项有关的参数;α2为与河床和冰盖阻力特性有关的参数。
式(9)的推算正是由Tsai等通过式(5)、式(6)合并而成。
以上分析结果表明,从分形理论出发,通过适当整合转化,能推出不同形式的冰下水流流速分布公式。
3.3 冰盖下水流流速垂线分布分析采用野外观测的垂线流速数据组进行冰下水流垂线流速分布的规律分析,其中什四份子弯道3 个断面共34 组、头道拐水文站大断面11 组。因ADCP 上下测流盲区的限制,冰盖下和河床上的局部区域无实测流速值,受冰盖与河床糙率影响,冰盖底部和河床表面流速很小,常以0值处理,限于篇幅,仅给出1、3断面中典型垂线的分析结果(图4)。由于河槽不同区域分布有厚度不一的冰花,ADCP实测流速均为冰下有效水深的流速。
3.3.1 弯道处(什四份子) 1 断面5#孔和21#孔分别为凹(左)岸和凸(右)岸两侧主流中水深较大的孔位,不难看出,无论是ADCP实测的全流速(非严格意义上整个水深的全部流速),还是以冰封期六点法从中提取的流速(ADCP多点测量与流速仪单点测量结果一致性较好[25]),垂线上最大流速点的位置均位于水深的中上部分(图4(a)),但更接近中部。由于最大流速点位置与冰盖和河床糙率有关,当二者糙率相等时,最大流速点位于水深中央,因此,以0.5h为界,将整个水深分为上下两层。因最大流速位置偏向光滑一侧,说明1断面冰盖底部的糙率小于河床表面糙率,但相差不大。反观3断面2#孔和12#孔的测量结果,ADCP 实测的垂线流速,由于冰盖区和河床区流速最大值非常接近,最大流速点难以界定,仅能从单点值大小判断最大流速位于上层水深;而六点法中的最大流速则位于下层水深(图4(b)),这种差异其实与水流的脉动作用及时均效应有关。事实上,通过对34组测流结果的分析,ADCP实测最大流速点所在区域与六点法得出的结果吻合度达90%,34组测流中,垂线最大流速点位于上层水深的占85.3%,且多接近于0.5h,表明此试验阶段,冰盖底部相对平滑,冰底糙率与河床糙率趋于平衡,在水深较浅的垂线(12#、7#)上也有类似特征。
弯道水流的特殊结构会引起流速重分布,冰盖下弯道水流在各向均有不同表现,主要取1、3 断面进行分析(图4)。流速沿纵向的重分布表现为:凹岸一侧水流流速沿程变化不大,平均流速变幅在0.1 m/s 以内,凸岸一侧水流流速基本不变,维持在1.0 m/s 左右,最大流速贴近凸岸;流速沿横向表现为:凹岸一侧水流平均流速(0.7 ~0.8 m/s)小于凸岸(0.9 ~1.0 m/s),中部流速最小(0.5 ~0.6 m/s),原因是凹岸一侧水流受护岸回推及顶托产生的回流影响,水流动能削弱,且凹岸一侧冰花较厚(疑为冰塞),冰花对水流产生的阻力也会降低水流流速;流速沿垂向表现为:冰盖区和河床区流速分布较为均匀,且平均流速大小相近。总体来看,各测点水流流速垂线分布呈“震荡”型式,尚不能清楚辨识流速分布规律,因此,需要采用数学方法进一步分析其分布特性。

图4 什四份子弯道部分点位流速垂线分布
分析冰下水流结构,利用双对数分布公式进行流速拟合。由式(7)可得:

式中:A为某一常数;B为斜率。
以ADCP 流速起止点为参考点,对上下盲区进行线性内插(流速近似线性增大)。选取1断面中两条典型垂线,按照式(10)进行拟合,结果如图5。结果表明,ADCP 实测冰盖区与河床区的流速均具有分形特征,用双对数分布公式对流速分布的表达效果较好,但在流动核心区,点群偏离拟合直线且分布较为集中,表明核心区流速并不服从对数分布,与茅泽育等[15]的研究结果一致。因此,针对不同需求,利用冰下水流流速垂线分布公式时需考虑其适用性。
对ADCP实测水流流速分布进行分维计算。因弯道水流流态复杂,流速混乱,故在建立线性趋势的基础上遴选出符合趋势的流速点。分维计算公式可简要概括为[26]:

图5 什四份子弯道1断面流速双对数分布

式中:C为系数;D为分维值。
选取水深值较大的几条典型垂线进行流速分布的分维计算,选定的垂线覆盖两侧河槽,率定结果具有代表性。统计的分维值能反映分区水流流速的分布特性,其大小可以表征挟沙水流流速分布的均匀程度,对冰下泥沙及污染物浓度分布、水流离散程度及挟沙能力的研究有参考意义。计算结果如表3。

表3 典型垂线流速分布的分维结果
分析典型垂线的流速分布的分维值。结果表明,冰盖区水流流速D值范围为0.70 ~0.93,在河床区则为0.01 ~0.95,冰盖区的D值明显大于河床区(除12#),说明弯道处的冰盖水流,其冰盖区的流速分布比河床区更为均匀。对比弯道两侧河槽,1 断面凹岸一侧水流冰盖区流速的D值小于凸岸,3断面则相反,说明1 断面凹岸一侧冰盖区流速分布比凸岸均匀,在3 断面出现异岸转移;1 断面凹岸一侧河床区流速D值也大于凸岸,但3断面无明显规律。由于3断面为弯顶段,最容易卡冰,受弯顶护岸顶托及回流作用,水流会发生明显的掺混,同时,3断面凹岸河槽存在大量的冰花,加上弯顶螺旋流影响,多因素叠加作用使得该断面水流分布不均匀。

图6 头道拐水文站流速垂线分布
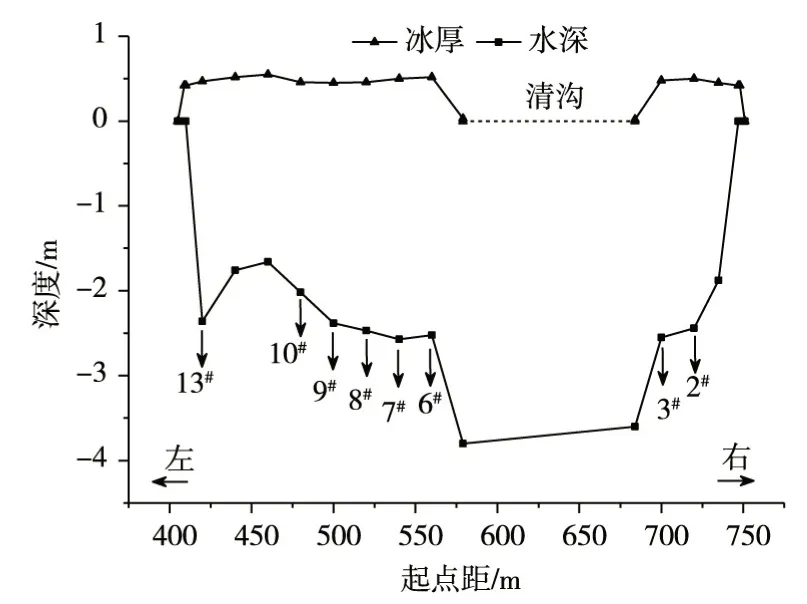
图7 头道拐水文站冰厚、水深分布
3.3.2 直道处(头道拐水文站) 头道拐水文站的三点法测量结果中,冰下水流流速垂线分布呈明显的镜像结构,分形特征显著,表明分形理论也能应用于直河道的冰下水流结构研究。大断面近岸两侧流速小,沿河宽方向流速逐渐增加,清沟左侧主流流速大于右侧,冰盖下河道左右侧的流速垂线分布非常一致,最大流速点基本位于水深中央(图6),而左右侧水深分布不均(图7),说明冰下水流最大流速点的分布与水深大小无关,当然,这也只是因为三点法只选取了0.15、0.5、0.85 m 水深处的流速,实际上最大流速在上下层水深均有可能存在,要获得准确结果,需多次进行加密测量,但同时会明显增加工作量;在处理一些工程实际问题时,由于最大流速点很难准确界定,只需获得其大概位置即可。对二点法、三点法测流试验的评估[31],冰期采用的二点法、三点法等点测量方法,测流误差较小,利用双幂律分布公式拟合,结果良好,说明冰期采用三点法得到的测流结果是合理的,能概化冰下水流结构。相较于ADCP 测流技术,由于三点法漏测了许多垂线点,因此对流速垂线分布的概化偏于理想化,但总体上,三点法实测直河道的冰下水流垂线流速分布仍具备良好的分形特性,基于分形理论推求的冰下水流垂线流速分布公式仍可沿用。计算水文站各测点水流垂线流速分布的分维值,冰盖区D值范围为0.50 ~0.97,河床区则为0.07 ~0.70,仍表现为冰盖区流速分布比河床区均匀,而清沟左右两侧水流流速分布的D值差异不大,表明河槽两侧流速分布的一致性较好。
无论是弯道还是直河道,冰下水流流速垂线分布在冰盖区和河床区均具有分形特征,能用双对数分布或双幂律分布进行描述。然而对于弯道,受双层反向环流影响,冰盖区和河床区水流流速分布较为均匀,且大小相近,表明在有冰盖影响下,水流流速在流动核心区一定范围内并不服从对数分布。因此,对不同河型,运用冰下水流流速分布公式时,需考虑适用性或引入因子项。
4 结论
以黄河内蒙古什四份子弯道和头道拐水文站直河道为研究对象,基于分形理论对冰盖下水流流速的分布规律进行了研究。(1)分形理论不仅可以应用于明渠水流,对冰盖下水流流速垂线分布同样适用,通过分形理论可推出冰盖条件下水流流速垂线分布公式;(2)冰盖下的水流分布,无论是冰盖区还是河床区,其流速垂线分布均具有分形现象,能用双对数分布公式表达;然而,弯道水流垂线流速在水流核心区不服从对数分布。因此,对不同河型,使用流速分布公式需考虑公式的适用性或引入其他因子项(如环流因子);(3)稳封期,最大流速点接近水深中央,冰盖糙率多小于河床糙率,但差值不大,体现为二者逐渐向平衡态逼近。冰盖区水流流速分布的分维值大于河床区,流速分布沿水深方向均匀化,但对弯道而言,弯顶处受冰花堆积与水流掺混影响,河床区水流流速分布的分维值不规律。
推求的冰下水流流速分布公式,完善了分形理论在水流流速垂线分布方面的研究。由于糙率对水流结构的影响显著,而冰盖糙率在整个封冻期一直处于动态变化中,研究只涉及了稳封期的流速分布,因此,需要进一步分析封河过程前期、后期冰盖糙率的变化对水流流速垂线分布的影响,同时,应当考虑流速公式在天然河道的可移植性并适当予以修正,提升基于分形理论推求的流速分布公式在不同工况下的普适性及准确度。

