高碾压混凝土重力坝分区材料-结构界面特性与变形协调仿真分析
李明超,张梦溪,沈 扬,冯 达,闵巧玲
(1. 水利工程仿真与安全国家重点实验室,天津大学,天津 300350;2. 中国长江三峡集团有限公司,北京100038;3. 华电重工股份有限公司,北京 100070)
1 研究背景
21 世纪以来,我国水利工程建设进入自主创新、引领发展的阶段,在大江大河上建造水利工程,大坝是核心的主体建筑物,其安全性是整个工程的关键。而坝体分区的不同部位因工作条件不同,设计时所采用的混凝土强度及其防渗、抗冻、抗冲刷和抗裂等功能也有所不同[1],因坝体各部位“结构特性”与“材料性能”的差异产生的变形协调问题,直接关系到工程结构的质量和耐久性。以面板堆石坝和心墙堆石坝为代表的坝体结构中,堆石坝体各区材料的宏观和细观变形特性、堆石坝体与面板或心墙变形的同步协调已成为变形安全的核心问题[2-4];以混合坝、多材料坝为代表的新型坝工结构中,连接部位和材料界面的变形协调关系到工程全局安全[5]。新材料与新结构的提出也为变形协调分析提出了更高的要求[6]。因此,高坝分区结构的异种材料的变形协调问题应引起足够重视。
实际上,复合材料、结合材料已在机械、航天工程领域广泛使用,复合材料的结合部统称为材料界面,荷载作用下材料界面往往是结构的“薄弱环节”[7-8],原因在于:(1)界面两侧材料因变形特性的差异而互相约束,使界面附近出现较高的应力水平(理论上无穷大),即应力奇异性;(2)目前施工质量水平难以保证界面处的完美结合,必然会存在一定缺陷,这些缺陷会在工程实践中逐渐劣化,影响结构稳定与安全。界面力学是一门因工程技术发展催生的年轻学科,近年来得到长足的发展,Bogy[9]通过Mellin 变换,推导了双材料弹性平面界面端应力解析解,指出了界面端应力奇异性的存在;许金泉[10]则分析了界面端与界面裂纹的奇异应力场,提出了界面裂纹与界面端的断裂准则;Sator 等[11]和Carpinteri 等[12]采用复变函数方法推导了双材料与多材料平面界面端部的应力奇性指数特征值λ的求解方法;田帅[13]开展聚碳酸酯-铝界面强度试验,分析了不同界面结合角度对界面强度与应力奇异性的影响;李兴民等[14]则采用数字相移光弹性方法,通过四点弯曲试验和数值模拟对比分析了铝合金/环氧树脂界面端的应力奇异性;黄平等[15]重点研究了摩擦学中的界面力学问题,从细观角度剖析了固体、流体以及流-固界面的作用机制,极大地丰富了界面力学理论。界面力学理论与试验研究为结合材料的强度可靠性提供理论依据,同时为新材料、新结构的设计提供理论指导。
碾压混凝土(Roller Compacted Concrete,RCC)重力坝中因分区设计而存在多种材料界面,在材料层面,国内外学者针对RCC 层面的力学性能和抗渗性能的变化规律、新老混凝土结合面的黏结强度、异种材料界面的力学性能开展了试验与模拟研究。孔祥芝等[16]应用直剪法测试RCC试件抗剪强度,研究了溶蚀作用对混凝土层(缝)面抗剪强度的影响;娄亚东[17]通过试验研究了碾压混凝土层面抗渗性能和抗剪强度随层间间隔时间的衰减规律;文献[18]基于小型碾压试验,研究了碾压参数对层间结合强度的影响;文献[19]采用铺设分散砾石的界面处理方式提升自密实混凝土新老界面结合强度;冯炜等[20]提出一种测试大坝全级配混凝土界面力学性能的试验分析方法,对三峡大坝混凝土的界面强度进行了测试研究;文献[21-22]结合碾压试验,研究了RCC 坝功能梯度结构中高性能混凝土与碾压混凝土界面力学性能规律,同时结合单轴压缩与斜剪数值模拟,提出了适用于常态-碾压混凝土复合试件的抗剪强度准则。对于高坝分区结构的变形协调特性,主要涉及心墙堆石坝的拱效应分析[23]与面板堆石坝的变形协调设计理念[24],关于混凝土坝分区结构变形协调分析研究较少,徐娜[25]和李明超等[26]通过接触分析评价了功能梯度结构过渡层结构形式、弹性模量等对碾压混凝土重力坝分区变形协调的影响;胡昱等[27]开发了一种适用于含界面工程结构的界面层单元,并成功应用于溪洛渡拱坝横缝变形的仿真计算。
上述研究大多通过材料试验或数值模拟的手段,分析荷载作用下碾压混凝土坝结构界面的强度特性、接触变形与受力状态等特性的变化规律,对荷载作用下RCC 坝界面处异种材料的相互作用与变形协调机理认识不足,未考虑因界面两侧材料特性差异产生的奇异应力场的影响,而当奇异应力场存在时,界面破坏不能以应力作为评价参数,需采用描述奇异应力场大小的参数来评价变形协调性。现阶段,碾压混凝土坝建设达200 m级,大坝建设重心逐渐向高寒、高海拔地区转移,筑坝材料趋于多元化,筑坝技术则不断向着精细化、智能化发展,坝体中薄弱部位(层面、界面)的性能提升与控制方法将逐渐成为决定大坝能够适应严苛的服役环境的关键科学问题。在工程设计阶段,变形协调问题尚未在考虑范围之内,同时受限于数值模拟手段和计算能力,大多研究仅对典型坝段进行复核分析,难以在较短时间内开展考虑所有材料分区的全坝段精细数值模拟计算,缺少分区材料-结构变形协调的快速评价方法,需对此展开深入研究。
考虑到上述问题,本文基于界面力学理论,选取应力奇异性特征值作为异种材料变形协调的评价指标,根据碾压混凝土坝实际工程中双材料的布置形式,推导双材料界面端与埋入角点的应力奇异性特征值计算方程,通过有限元数值计算验证了所推导方程的正确性与有效性;改变界面端与埋入角点的结合角度,计算界面两侧材料的弹性模量与泊松比的差异对应力奇异性的影响,并结合实际工程分析坝体内部双材料界面端与埋入角点的奇异性,初步总结碾压混凝土坝分区结构材料特性选取与设计原则,为高混凝土坝分区结构设计与材料选取提供新的思路。
2 双材料界面奇异性特征方程

图1 碾压混凝土坝双材料常见布置形式
在碾压混凝土坝中,两种不同材料的结合主要有图1所示的两种布置方式,即单侧自由的界面端与埋入式角点。文献[27]计算了横缝分别为理想界面、薄层界面和有厚度界面层情况下,溪洛渡混凝土拱坝横缝处正应力,结果表明界面层特性的变化对于大尺度水工结构影响不大,因此,本文假设混凝土材料界面为理想结合面,界面处的应力与位移均满足连续边界条件,对于图1(a)所示的异种材料界面端,在极坐标(r,θ)下,则界面连续的边界条件和自由边界条件可表达为:

对于图1(b)所示的埋入式界面角点,界面连续的边界条件可表达为:

式中:σγi、σri分别为界面处第i种材料的环向应力与径向应力;uγi、uri分别为界面处第i种材料的环向位移与径向位移;γ取值范围为0 ~180°。
对于图1(b)所示埋入式界面折点,可将其分解为对称结构和反对称结构,根据界面连续的边界条件可得决定奇异应力性的特征方程分别为:
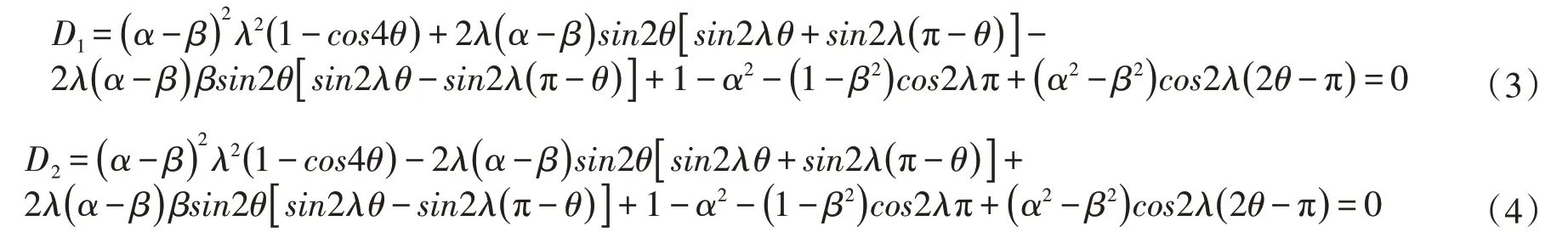
式中,α、β分别为Dundurs和Bogy定义的结合材料参数:
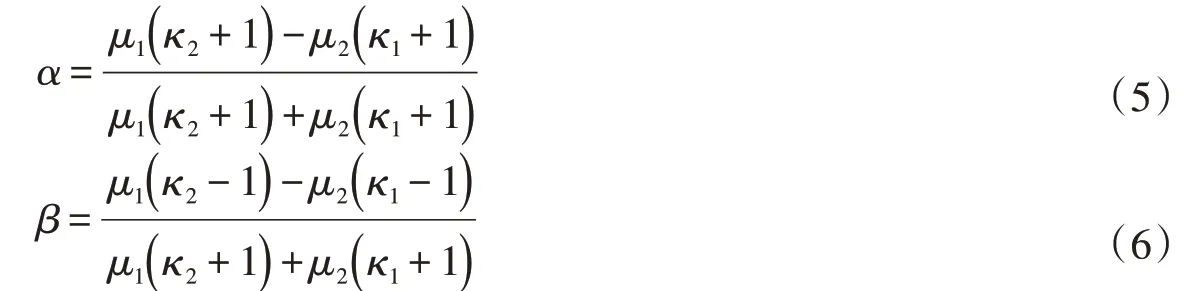
式中:μ为剪切模量;κ为Kolosov 常数[11];λ为表征异种材料界面端奇异性的特征值;E、ν分别为材料的弹性模量和泊松比。

已有研究表明,界面应力与应力奇异性特征值λ直接相关,当r→0时,界面附近应力场可表示为式(8)的形式(不考虑对数奇异应力性)。因此,考虑采用式(3)和式(4)的特征解λ作为评价异种材料界面变形协调特性的主要指标。

其中O表示同阶无穷小量符号。
3 数值模型验证
3.1 有限元模型与实验参数为验证特征方程求解的可靠性,同时考虑界面端与埋入折点两种界面形式,建立如图2所示的双材料复合试件模型,外侧边界为单侧自由界面端,中间部分为界面埋入折点,模型尺寸为600 mm×200 mm,界面与自由面夹角为θ,两侧界面的夹角为2θ,其中0°≤θ≤180° 。取该模型的对称形式,建立有限元模型,界面处对网格细化处理,网格尺寸达10-4m量级,验证模型中两种材料弹性力学参数取为:E1=40 GPa,E2=20 GPa,ν1=ν2=0.167。加载方式为单轴压缩加载,压力P=10N/m,改变界面角度θ,计算界面处应力分布情况。

图2 双材料复合试件验证模型
3.2 应力奇异性验证以O为坐标原点,提取界面OA的正应力分布如图3所示,r为以O点为原点的极坐标半径。从图3 可以看出,当r→0 或r→W时,应力梯度越大,表明应力奇异性越强,反之应力分布越平缓,奇异应力性越小。所以根据界面处应力分布可得到以下结论:(1)当0°≤θ<90° 时,埋入折点的应力奇异性较90°<θ<180°时更强;(2)当θ=90°时,两侧界面夹角为180°,此时不存在界面折点,故O点处不存在应力奇异性,应力分布平缓;(3)当界面与自由面夹角取为θ时,界面中部分应力分布与其取为180°-θ时接近。
根据式(8)可知,应力分布与奇异性特征值λ呈指数关系,故考虑将数值模拟得到的界面正应力与极坐标半径r归一化后取对数,图4 为部分角度界面的外侧界面端应力与r外的关系曲线,r外表示以外侧端点A或B为原点的极坐标半径。从图4可见,二者的双对数表现为线性关系,得到的直线斜率即为λ-1,若斜率为负,则0 <λ<1,表明在接近端点处存在趋于无穷的应力分布(应力奇异性),且λ越接近1应力奇异性越弱;若直线斜率为正则表明在接近端点处存在趋于0的高阶微量应力分布,无应力奇异性。
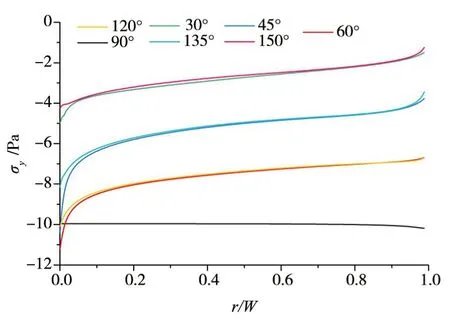
图3 界面OA的正应力分布
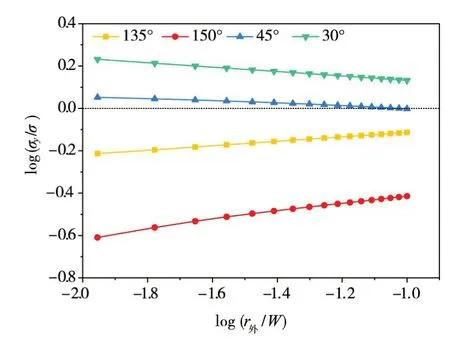
图4 正应力随极坐标半径双对数变化规律

图5 单侧自由界面端奇异性特征值数值解与理论解对比
由于界面埋入折点情况下,应力奇异性指数λ可能存在多个实根,无法用双对数求得特征值近似解,故考虑将单侧自由的界面端数值模拟计算结果与求解式(3)、式(4)得到的λ理论值进行定量对比验证,如图5所示,发现二者吻合良好,表明理论计算具有较好可靠性。

图6 不同布置角度下弹性模量的比值对应力奇异性影响

图7 不同布置角度下泊松比的比值对应力奇异性影响

表1 单侧自由界面奇异性消失条件
3.3 敏感性分析界面结构的布置形式与界面两侧材料参数是影响应力奇异性的重要因素。分别改变两种材料弹性模量的比值(E1E2)和二者泊松比的比值(ν1ν2)中的一个,固定另一个比值,计算得λ随夹角θ变化规律如图6、图7所示。从图6、图7可得到如下结论:(1)在0 <λ<1的情况下,E1E2与ν1ν2越接近于1,异种材料越接近均质材料,特征值λ越接近于1,且随夹角θ变化波动越小,变形协调性越好;(2)E1E2对应力奇异性影响大于ν1ν2对界面应力奇异性影响,工程设计时应将弹性模量比作为主要控制指标;(3)在不同界面形式下,应力奇异性在一定条件下会消失(λ≥1),如表1所示,在进行单侧自由界面材料设计时,当ν1ν2固定时,应保证弹性模量较高的材料自由面与界面的夹角小于63°。由于λ≥1 时界面端处应力为高阶无穷小量,在靠近界面端点处趋近于0,故后续应力奇异性分析仅针对0 <λ<1情况展开讨论,对于λ≥1 的情况不再计算具体应力奇异性特征值。
相比于单侧自由界面端,界面埋入折点的应力奇异性特征值λ变化规律截然不同,图8 为界面角度θ和弹性模量比E1E2对λ的影响,图中深红色区域为应力奇异性消失的情况。由此可得出以下结论:(1)埋入式界面折点存在1 ~2 个应力奇异性特征值,具有出现奇异应力的可能性;(2)E1E2越接近1,θ越接近90°,埋入界面折角越接近180°应力奇异性越小;(3)E1与E2差异越大,奇异性特征值越小,应力奇异性越大;(4)由于混凝土材料间差异不大,并未产生小于0.83 的应力奇异性特征值,变形协调性相对良好。因此,在进行埋入结构设计时,应尽量保证埋入界面折角接近于直线,同时减小界面两侧材料特性的差异,降低应力奇异性,提高结构的变形协调特性。
4 坝体分区材料-结构变形协调分析与评价
4.1 分区材料变形协调仿真分析实际上,由于混凝土为典型的非线性材料,在荷载作用下材料会发生损伤破坏,界面位置的应力不可能变为无穷大。因此,本节从材料角度出发,考虑混凝土损伤情况下,分析包含界面折点与单侧自由界面端的混凝土复合试件强度与奇异性指数λ的关系。着重讨论此时应力奇异性指数λ能否用来表征非线性材料界面变形协调特性。基于非均质有限元法,对每个单元赋予服从weibull 分布的材料参数,混凝土本构采用弹性损伤模型,破坏准则满足摩尔库伦和最大拉应力准则,计算时保持泊松比一定,现定义界面上方为材料1、下方为材料2,固定材料1 的材料参数,为着重分析弹性模量差异的影响,在改变材料2弹性模量的同时保持其强度不变,分别计算E1/E2为1.066、1.278、1.911以及2.594的复合试件在不同界面布置形式下的抗压强度,所选材料参数如表2 所示。图9 为θ=30°时3 种弹性模量比组合的复合试件破坏形式。从图9 可以发现,破坏在界面附近出现逐渐向强度较弱材料扩展,表明存在应力奇异性,且随着弹性模量差异的变大,应力奇异性增大,界面折点处破坏逐渐变大。
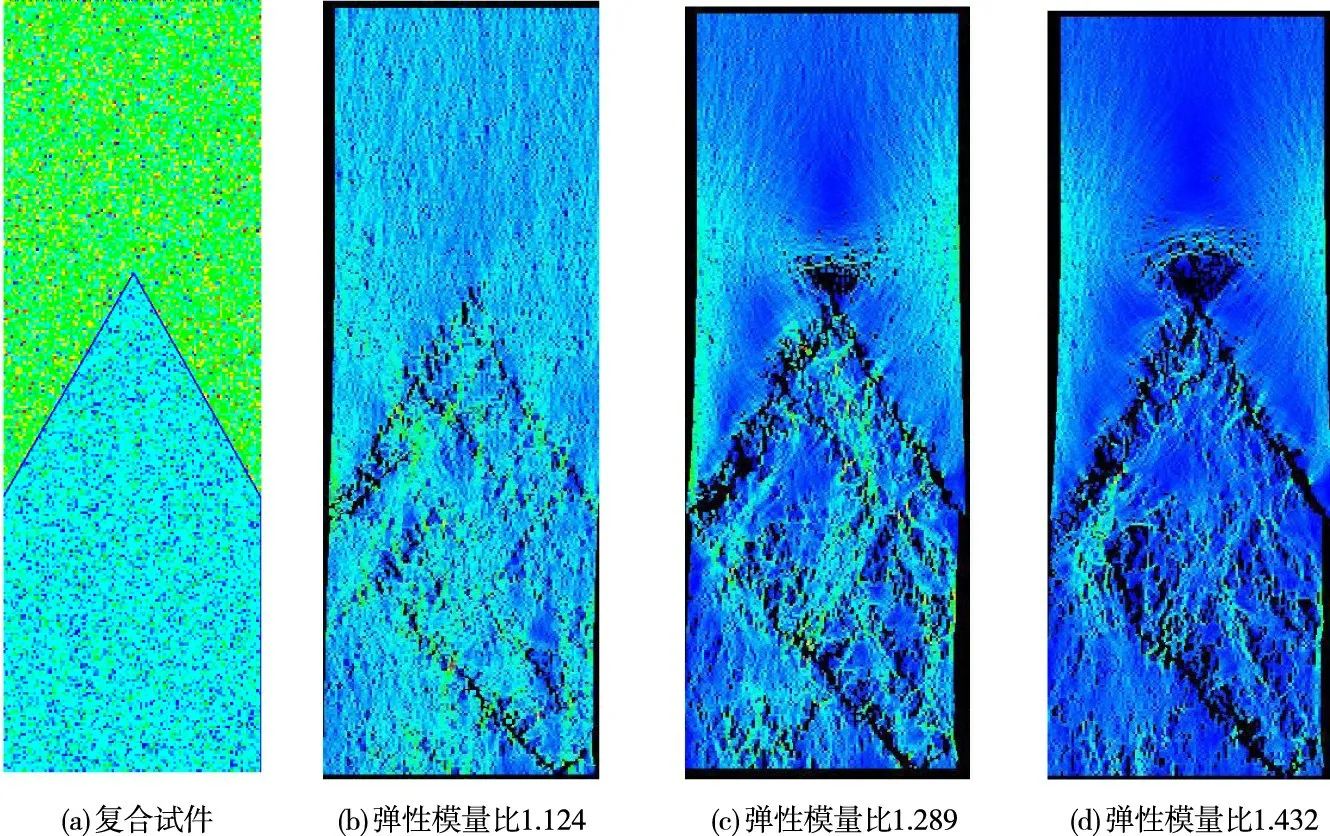
图9 复合试件破坏形式
改变界面的结合角度,同时保证两种材料用量各占一半,通过单轴压缩加载,得到角度θ在15°~165°范围内变化时,复合试件的破坏形式(图10)与破坏强度(图11)。
从图10、图11 可以看出:(1)复合试件的基本失效模式为破坏由界面折点处产生并沿材料界面扩展;(2)当界面折点尖端外侧材料弹性模量和强度较高时,如图10(a)—(d)中的材料1 仅在折点尖端部位出现破坏,其他部位相对完整,未出现贯穿性破坏;当界面折点尖端外侧材料弹性模量和强度较低时,如图10(f)—(i)中的材料2发生严重破坏,材料1则几乎未发生破坏;(3)界面两侧材料的弹性模量差异越大,破坏越集中于界面处,表明两种材料变形协调性越差,复合试件的强度越低;(4)复合试件强度随θ变化而变化,且取为30°或150°时强度最低;θ=90°时不存在界面折点,复合试件主要表现为强度较弱材料的破坏。
为分析应力奇异性特征值对复合试件强度的影响,以抗压强度为横坐标、λ为纵坐标建立图12所示相关分析图。从图12可以看出,在考虑混凝土材料损伤破坏的影响后,二者相关系数R=0.905,表现为强相关关系,即应力奇异性特征值λ越小,材料间变形协调性越差,复合试件抗压强度越低。因此,高碾压混凝土坝分区材料设计时,采用λ来表征界面两侧材料间的变形协调特性具有可行性,能够直观的反映异种混凝土材料间的变形协调特性,可在大规模高精度的数值模拟和试验之前对工程分区材料变形协调特性进行快速评价,进而实现高碾压混凝土坝分区材料-结构的安全设计。
4.2 分区结构变形协调仿真分析在工程设计时,难以建立全坝段完整的数值模型,且模型往往会进行简化,存在舍弃关键信息的可能性,极大地限制了数值仿真工作的开展,无法对结构变形和受力进行准确的分析。以我国西南地区某水电站工程为例,对工程中界面折点与界面端开展应力奇异性分析。该水电站工程开发任务以发电为主,同时改善航运条件,兼顾防洪、灌溉,电站为一等工程,工程规模为大(1)型。工程枢纽挡水建筑物为混凝土重力坝,坝体内存在多处单侧自由界面端与埋入折点,典型布置形式如图13所示,RI、RII、RIII代表不同粉煤灰掺量、不同级配、具有不同力学特性的碾压混凝土或常态混凝土。
现以a型表示单侧自由度界面端(图13(a)),b型表示埋入式界面折点(图13(b)),收集并统计该工程中典型双材料界面两侧材料参数与界面布置形式,并计算应力奇异性特征值如表3所示。从表3可见:(1)该工程中单侧自由界面端(形式a)除90°结合部位之外,特征值λ均有唯一实数解且均大于1,表明该结构形式与材料组合下不存在奇异应力性,变形协调特性符合要求;(2)对于埋入式界面折点,特征值λ均存在1 ~2 个小于1 的实数解,分区材料的界面处存在应力奇异性,但应力奇异性特征值λ均大于0.97,分区混凝土材料间的变形协调问题尚在可控范围;(3)对于界面形式b,该工程左厂⑥、升船机、泄④坝段出现了界面折点尖端外侧材料弹性模量和强度较低的情况(E1<E2,0°≤θ<90° 或E1>E2,90°<θ≤180°),受界面折点的约束作用产生的应力更容易导致外部材料发生劈裂破坏(如图10(f)—(i)所示),因此在类似工程分区结构设计时,需考虑调整埋入角点的布置形式或采用适当的防护措施。

图10 不同结合角度下复合试件破坏模式

图11 不同界面结合角度下复合试件抗压破坏强度
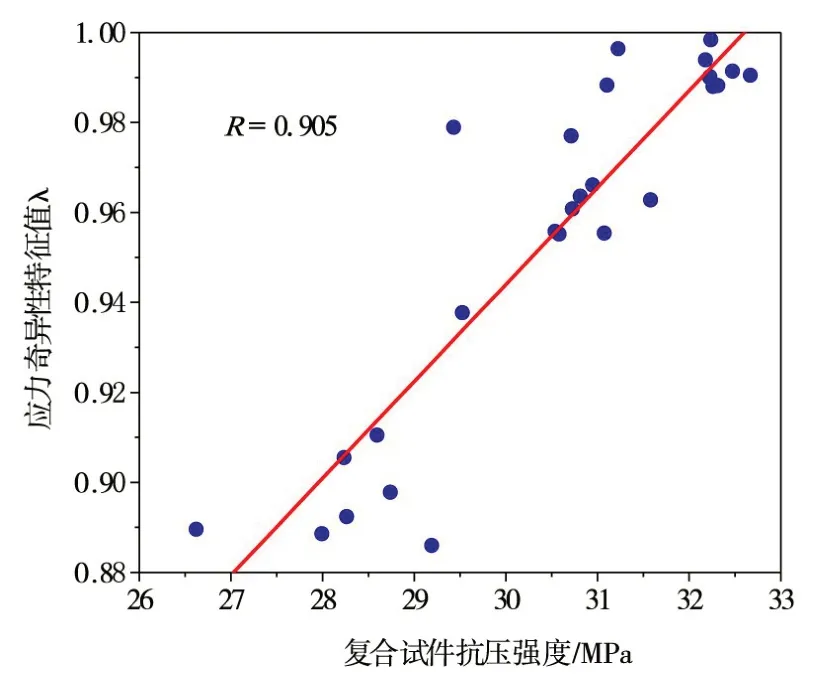
图12 复合试件抗压强度与应力奇异性相关分析

图13 混凝土坝分区双材料典型界面形式

表3 某工程典型双材料界面应力奇异性
5 结论
本文采用界面力学理论,以应力奇异性特征值作为异种材料变形协调的评价指标,考虑混凝土坝分区中常见的两种双材料界面形式,分析了界面结合角度和异种材料组合对应力奇异性的影响;研究了复合试件界面处的破坏模式,计算了实际混凝土坝工程中不同坝段内的双材料界面的应力奇异性特征值,得出以下结论:(1)在材料层面,异种材料的力学特性差异越大,界面处奇异应力性越强,复合材料强度越低,越不利于结构变形协调控制;(2)在结构层面,改变双材料界面端或界面折点的结合角,直接影响界面两侧材料的变形协调特性,在结构设计时应重点考虑;(3)实际工程中,单侧自由的界面端应力奇异性弱于埋入式界面折点,设计时应着重考虑优化界面折点的材料组合与界面的结构形式。
混凝土材料界面破坏与界面强度及受力状态有关,本文主要考虑了材料与结构对受力状态的影响。实际上,坝体混凝土界面往往存在一定缺陷,并非理想的黏结状态。因此,考虑缺陷对界面强度的影响,进一步提炼混凝土坝分区材料-结构的定量设计准则,具有重要的工程意义。

