Detumbling strategy based on friction control of dual-arm space robot for capturing tumbling target

Gng CHEN, Yuqi WANG, Yifn WANG, Ji LIANG, Long ZHANG,Gungtng PAN

a School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China

b Key Laboratory of Space Utilization, Technology and Engineering Center for Space Utilization, Chinese Academy of Sciences, Beijing 100094, China

KEYWORDS Detumbling strategy;Dual-arm space robot;Free-floating base;Friction control;Tumbling target capturing

Abstract The rotational motion of a tumbling target brings great challenges to space robot on successfully capturing the tumbling target.Therefore,it is necessary to reduce the target’s rotation to a rate at which capture can be accomplished by the space robot.In this paper,a detumbling strategy based on friction control of dual-arm space robot for capturing tumbling target is proposed. This strategy can reduce the target’s rotational velocity while maintaining base attitude stability through the establishment of the rotation attenuation controller and base attitude adjustment controller.The rotation attenuation controller adopts the multi-space hybrid impedance control method to control the friction precisely.The base attitude adjustment controller applies the dual-arm extended Jacobian matrix to stabilize the base attitude. The main contributions of this paper are as follows:(1)The compliant control method is adopted to achieve a precise friction control,which can reduce the target angular velocity steadily; (2) The dual-arm extended Jacobian matrix is applied to stabilize the base attitude without affecting the target capture task;(3)The detumbling strategy of dualarm space robot is designed considering base attitude stabilization, realizing coordinated planning of the base attitude and the arms. The strategy is verified by a dual-arm space robot with two 7-DOF (degrees of freedom) arms. Simulation results show that, target with a rotation velocity of 20(°)/s can be effectively controlled to stop within 30 s,and the final deflection of the base attitude is less than 0.15°without affecting the target capture task,verifying the correctness and effectiveness of the strategy.Except to the tumbling target capture task,the control strategy can also be applied to other typical on-orbit operation tasks such as space debris removal and spacecraft maintenance.©2019 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

Statistical data reveals that, with the deepening of space exploration, the number of failed or decommissioned spacecraft has increased year by year.1,2Those spacecraft do not have functioning attitude control, so in many cases they will be tumbling due to the transfer of residual angular momentum from their control systems.3,4The tumbling spacecraft not only waste valuable orbital space resources, but also threaten the safety of on-orbit spacecraft. For these reasons,many countries have carried out researches on tumbling target capture.5Common capture devices include flying claw, flying net and space robot.6-9Flying claw may damage the spacecraft, while flying net is easy to entangle. In contrast, using space robot can precisely control and operate the spacecraft,which is conducive to the spacecraft recycling.10-12However,because the tumbling target is in a floating state, using a single-arm robot is prone to disturb the target,causing the target to escape.13Considering that the dual-arm space robot can form an effective envelope area to prevent the tumbling target from escaping and increase the probability of a successful capture14,15, it is of great significance to do research on dual-arm space robot capturing a tumbling target.

The target’s rotational motion brings challenges to the tumbling target capture task.16Due to the target’s rotational motion, it may cause excessive contact force between the robot’s end-effectors and the target, which may lead to the damage of the contact interface.Moreover,due to the dynamic coupling between the base and the arms,it is difficult to maintain the base attitude stability during the capture task.17-19Base attitude instability may adversely affect the communication, energy and thermal control systems of the space robot.In severe cases, it may lead to the failure of the capture task and affect the safety of space robot system. Therefore, the key points of dual-arm space robot for capturing tumbling target,involve rotation attenuation and base attitude adjustment.Rotation attenuation means reducing the angular velocity of the tumbling target, which helps the space robot to track the target’s pose in the capturing task. Base attitude adjustment means maintaining the base attitude stability, which helps decrease the undesired interference caused by the robot arms motion and the captured momentum transfer during the execution of the target capturing task.

The general way to achieve rotation attenuation is by acting the external torque on the tumbling target. According to the contact state, the existing rotation attenuation methods can be divided into two types: contact type (reducing the target’s rotational velocity by mechanical contact force), and noncontact type (reducing the target’s rotational velocity by non-contact force such as gas pulse, electromagnetic force and laser).20,21The contact type can provide larger control force, and control the tumbling target more safely and reliably.20So many scholars choose this type to reducing the target’s rotational velocity. Nishida and Kawamoto22used a brush type contactor as the end-effector of a robot arm.Using the friction caused by deformation of the brush, the angular velocity of the target can be reduced. Wu et al.23developed a generic frictional contact model by considering the compliance contact force into bristle friction model. Analysis shows that friction can help avoid damage to robot system while reducing the target’s rotational velocity.24The reason is that the torque transmitted to the robot system is determined by the friction coefficient,and the large amount of energy absorbed instantaneously during hard capture can be converted into heat by friction and released slowly. Using friction is a safe and effective method, but Nishida and Wu did not control the friction precisely, causing the target attenuation velocity uncontrollable and robot system unstable. Therefore, an improved approach is followed herein, where the compliant control method is adopted to achieve a precise friction control,thereby reducing the target angular velocity steadily.

During the execution of the target capturing task, the attitude control system will be closed and the space robot will become a free floating system. Due to the dynamic coupling between the base and the arms, the robot arms motion and the captured momentum transfer may cause an undesired interference to the base attitude.25The stabilization of base attitude has been considered and several solutions have been proposed. Nakamura and Mukherjee26used the nonholonomic mechanical structure characteristics to control both the base attitude and the joint variables of the manipulator,but the obtained joint motion was not smooth.Yoshida et al.27proposed Zero Reaction Maneuver (ZRM) method to ensure base attitude undisturbed. However, the ZRM method was limited by the number of kinematic redundancy DOF. Also,it had a complex form and required a large amount of calculation.Jin et al.28combined the equations of motion of the base attitude and the generalized Jacobian matrix to obtain the extended Jacobian matrix, realizing the coordinated planning of the base and the manipulator. Based on the theory in paper28, the method is extended to the dual-arm space robot’s tumbling target capturing task. The dual-arm extended Jacobian matrix is applied to stabilize the base attitude without affecting the target capture task. This method can realize the coordinated planning of the base and two arms concisely.Moreover, the use of this method will not be limited by the number of kinematic redundancy DOF.

In summary,the dual-arm space robot provides advantages for capturing a tumbling target, but some problems for effective capture should be considered.Reducing the target angular velocity steadily is necessary for achieving a reliable capture,but the existing methods cannot precisely control the friction,resulting in uncontrollable rotation attenuation. At the same time, base attitude adjustment is necessary when the base disturbance is caused by the target capture operation, but the existing methods are limited by the kinematic redundancy DOF. Therefore, this paper proposes a detumbling strategy based on precise friction control.First,the detumbling dynamics model is established, which lays the foundation for the design of the detumbling strategy. Then, the rotation attenuation controller adopting the multi-space hybrid impedance control method is designed to control the friction precisely.On this basis,the base attitude adjustment controller applying the dual-arm extended Jacobian matrix is designed to stabilize the base attitude. This paper has three advantages as follows:

Combined assumption c)in Section 2.2,it follows that friction can generate torque to reduce the target’s rotational velocity. Thus, Eq. (12) can be rewritten in the following form

where

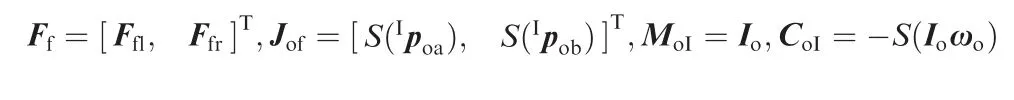
2.3.1. Calculation of contact force

The specific calculation of contact force (Fig. 4) is as follows.

(1) Calculation of the normal pressure

A spring-damped model is used to simulate the normal pressure in this case

In the above equation, K is the spring stiffness, D denotes the damping coefficient, Δp represents the normal small displacement.

(2) Calculation of the tangential friction

The research process of friction model can be mainly divided into static friction model stage and dynamic friction model stage. The static friction model cannot reflect the characteristic of frictional memory, so it has many limitations. In order to accurately describe the dynamic characteristic of friction, scholars have proposed a variety of dynamic friction models.32-35Among them, LuGre model contains only a few parameters and can easily be matched to experimental data.Therefore, in this paper, the LuGre model is applied.

The model is described by

where σ0is the stiffness,σ1is the damping,σ2is the viscosity,d represents the internal friction state, v denotes the relative velocity between the two surfaces in contact.

When dry friction exists,the stribeck effect can be ignored.In this case, the friction equation can be simplified as

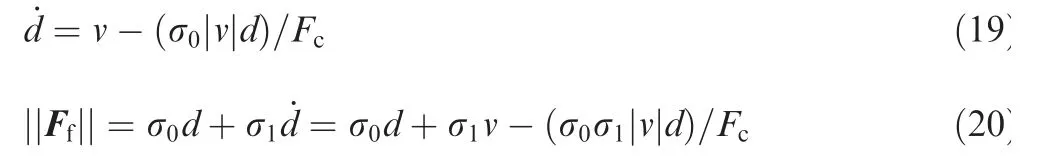
2.3.2. Relationship between contact force and relative motion

The Eq. (20) shows the relationship between the friction forcethe relative velocity v and the coulomb friction force Fc.For further derivation, we need to get the mathematical expression of relative motion.

The internal friction state d can be calculated by performing a Laplace transform on Eq. (19). Substituting d into Eq. (20)yields

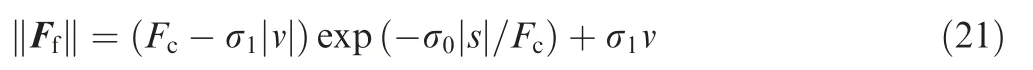
where s｜｜is the tangential relative displacement between the two surfaces in contact.

According to Eqs.(21)and(16),the desired relative motion can be written as

where Fc=μ Fn‖ ‖, μ represents the coulomb friction coefficient.

In Section 2.3, the contact dynamic model between the arm and the tumbling target is established. The normal pressure of the contact surface is deduced by using the springdamped model, and the dynamic characteristic of the friction force is described by the LuGre model. In this way,the mathematical expression of the contact force is obtained.In addition, the relationship between contact force and relative motion is analyzed. All the studies above lay the foundation for the design of the detumbling strategy based on precise friction control.

3. Detumbling strategy design for capturing tumbling target

In order to reduce the tumbling target’s rotational velocity steadily under the premise of ensuring the base attitude stability, the detumbling strategy of dual-arm space robot is designed considering base attitude stabilization based on the above models. In this paper, we adopt multi-space hybrid impedance control method to achieve a precise friction control, thereby reducing the target angular velocity steadily. On this basis, the dual-arm extended Jacobian matrix is applied to stabilize the base attitude without affecting the target capture task.

3.1. Rotation attenuation controller

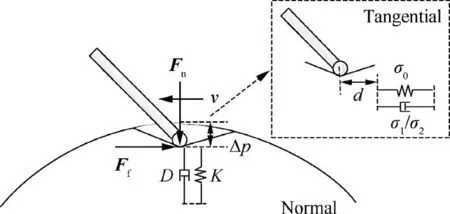
Fig. 4 Contact force of contact point.

A multi-space hybrid impedance method is adopted to achieve the precise friction control. The task-space impedance of the target is regarded as the external loop of the controller and the Cartesian-space impedance of the space robot as the internal loop. This method ensures that both the target and the arms have impedance characteristics. Fig. 5 shows the impedance characteristics formed between the end-effectors and the target.

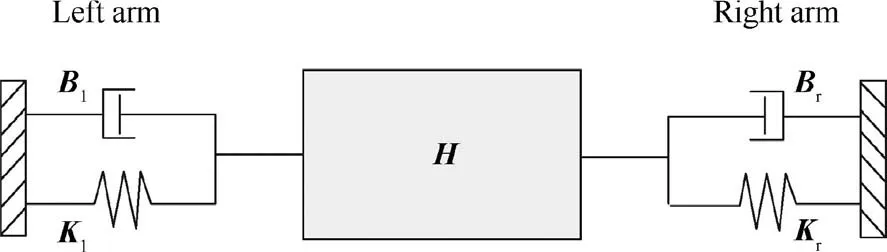
Fig. 5 Impedance model of the target.

3.1.1. Task-space impedance of the target

In this paper,the task-space impedance of the target is used as the external control loop. In order to construct the target impedance equation, a virtual external force term Fviris introduced(actually Fvir=0).The impedance equation of the target can be written as where Ho, Boand Korepresent the desired inertia, damping,and stiffness gains, respectively. ～Yo=Yo-Yod, with Yoddenotes the desired pose. In actual control, the controllable attenuation of target angular velocity can be achieved by setting Yod/˙Yod/¨Yod.

Solving Eq. (23) for acceleration, the desired input for the external control loop is obtained

3.1.2. Cartesian-space impedance of the space robot

The Cartesian-space impedance of the space robot is used as the internal control loop to establish the impedance relationship between the relative motion and the internal force. According to the results of Section 2.3, there is a coupling relationship between the normal pressure and the tangential friction force. That means the end output force is not mutually orthogonal and independent in all directions. This brings a challenge to the control of contact force.

Considering the expression of Ff‖ ‖(in Eq.(21)),the decoupling of the normal pressure and the tangential friction force can be achieved by controlling the relative motion between two contact surfaces. However, this approach brings a new problem: we need to control both the relative motion and the internal force,which is impossible to achieve by impedance control.

To fix this problem, the hybrid impedance control method36,37is applied to the Cartesian-space impedance of the space robot. The essence of hybrid impedance control method is to decompose the Cartesian-space of the space robot into impedance control subspace and force control subspace.In the impedance control subspace,the impedance relationship between the position and force of the robot system is adjusted in real time.The desired force tracking task is performed in the force control subspace.

The hybrid impedance control model of the space robot can be written as

denotes the desired relative motion,and the calculation details can be obtained from the Eq. (22).

The selection of the control subspaces is achieved through the selection matrix S and ¯S. When the diagonal element of S is 1, the impedance control mode is adopted in the corresponding direction with respect to the contact coordinate system. When the diagonal element of ¯S is 1, the force control mode is adopted in the corresponding direction. In particular,some directions do not take any control mode, which means that the corresponding elements of S and ¯S are both 0.

Solving Eq. (25) for acceleration, the desired input for the internal control loop is obtained

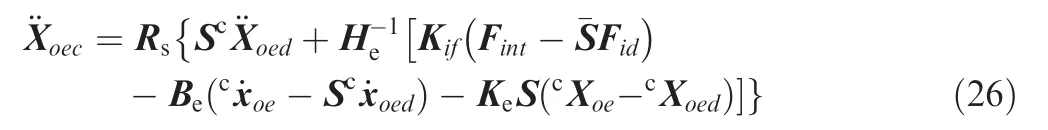
3.1.3. Multi-space hybrid impedance control

Substituting Eqs.(24)and(26)into Eq.(11),the desired input for the multi-space hybrid impedance method can be rewritten as follows

Substituting Eq. (27) into Eq. (4), the joint-torque control law of dual-arm space robot can be computed as follows

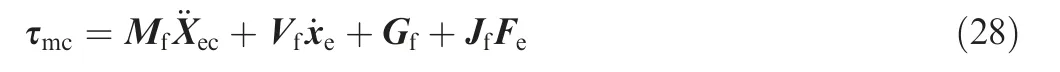
In Eq. (28), the multi-space hybrid impedance method is designed to achieve the precise friction control. We use the task-space impedance of the target as the external control loop, to establish the impedance relationship between the movement of the target and the virtual external force. We use the Cartesian-space impedance of the target as the internal control loop, to establish the impedance relationship between the relative motion and the internal force. The decoupling of the normal pressure and the tangential friction force can be achieved by controlling the relative motion between the arms and the target,which makes it possible to control the end contact force precisely. Thereby we can reduce the target angular velocity steadily.

The proposed control structure is shown in Fig. 6.

3.2. Base attitude adjustment controller

The dual-arm extended Jacobian matrix is applied to stabilize the base attitude without affecting the target capture task.The coordinated planning of the base and two arms can be realized concisely.

In the microgravity environment, the angular momentum and the linear momentum of the free-floating system (with the target) are conservative without the influence of external forces. The angular momentum and the linear momentum of the combined system can be written as

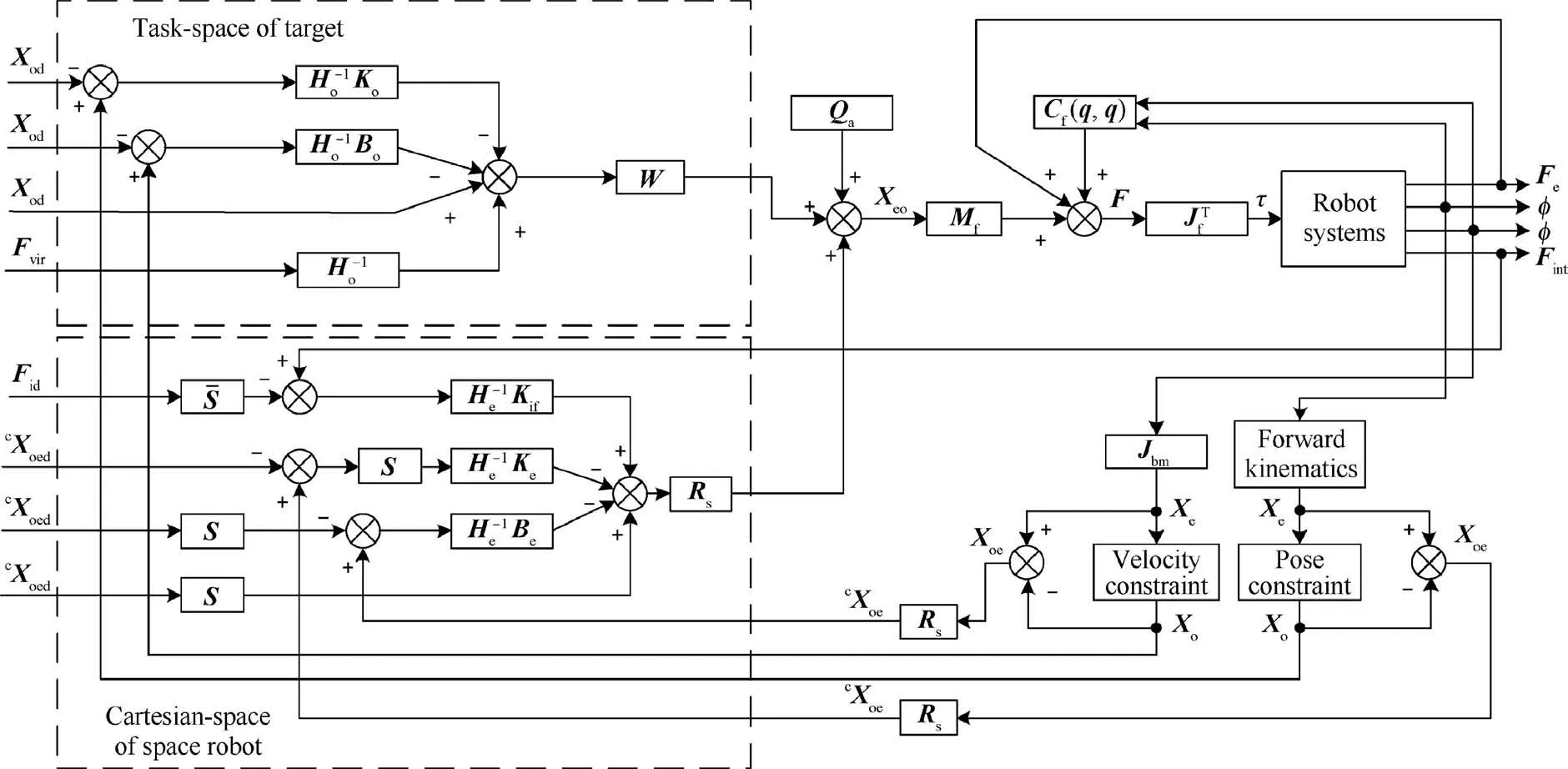
Fig. 6 Multi-space hybrid impedance control structure of the dual-arm space robot.

Prsand Lrsdenote the linear and angular momentum of the dual-arm space robot system, respectively.

Substituting Eqs. (30) and (31) into Eq. (29), the angular momentum and the linear momentum of the combined system can be written as follow

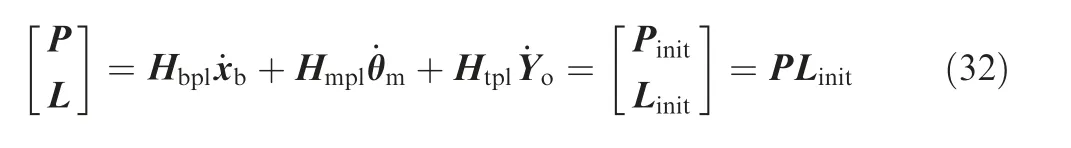
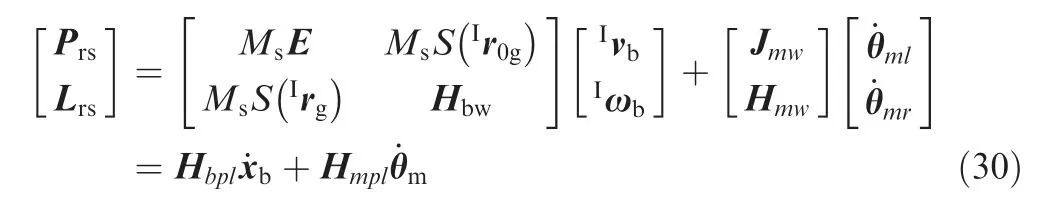
where Pinitdenotes the initial linear momentum of the combined system, Linitdenotes the initial angular momentum of the combined system.

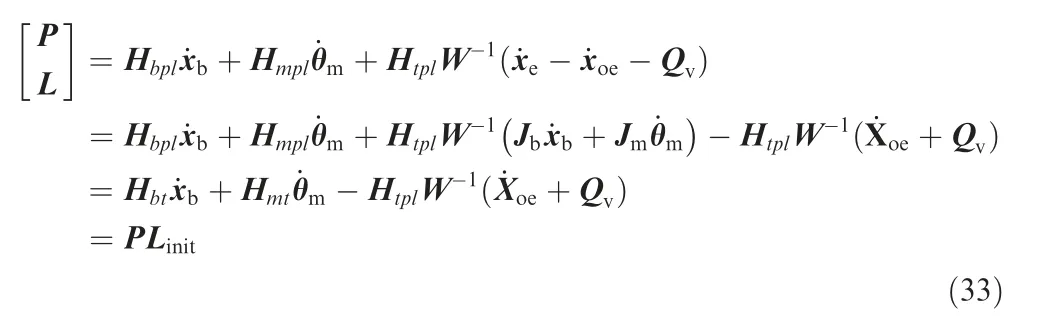
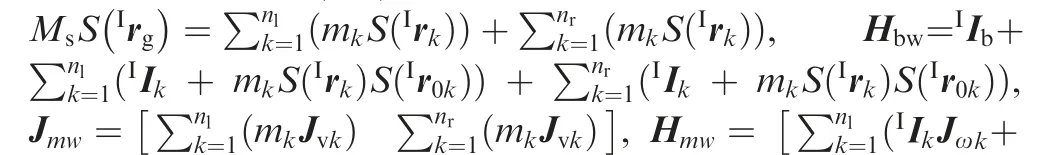
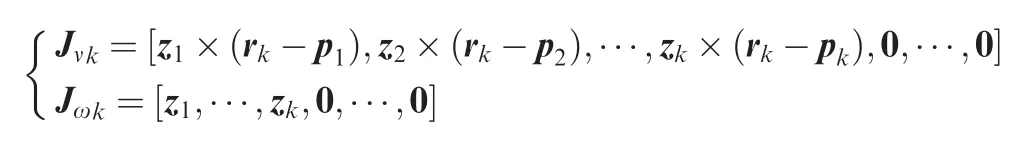
where Hbt=Hbpl+HtplW-1Jb, Hmt=Hmpl+HtplW-1Jm.

From Eq. (32), the mapping relationship between base motion and joint motion is as follow

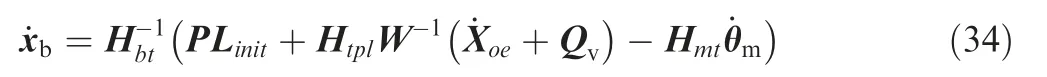
The general motion equation of dual-arm space robot system can be rewritten as

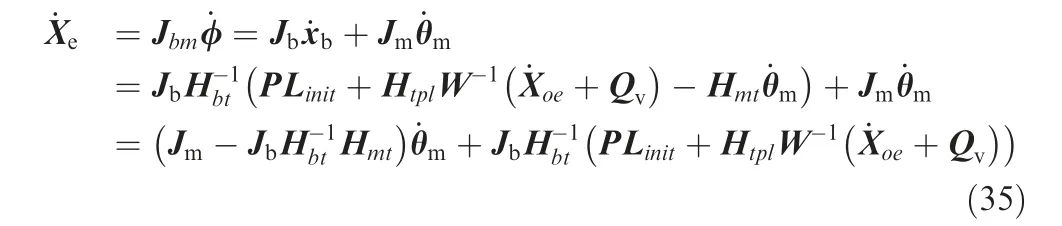
where zkis z axis of the frame at joint-k, pkis vectors of position from the frame origin at joint-k to the inertial origin, Pttand Lttdenote the linear and angular momentum of the target,respectively.

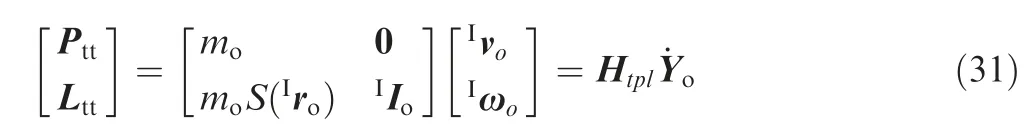
withIrorepresenting the vector of position from the center of mass of target to the inertial origin with respect to the inertial frame ΣI.Jacobian matrix. Different from the generalized Jacobian matrix Js, Jgnot only includes kinematic parameters such as the length of the links, but also includes the dynamic parameters such as mass and inertia of the links, as well as the base parameters and target parameters.

Substituting Eqs. (34) and (35) into Eq. (1), the kinematics equation can be rewritten as follow

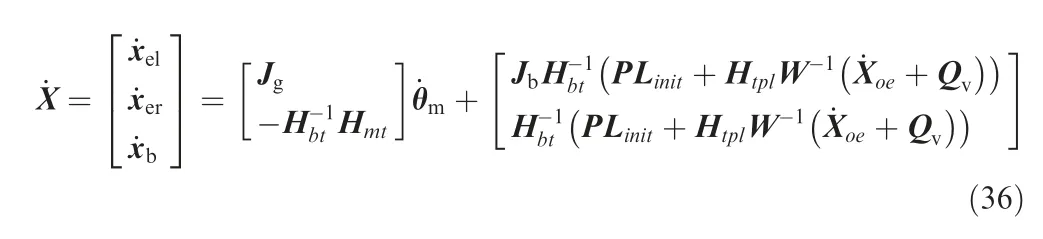
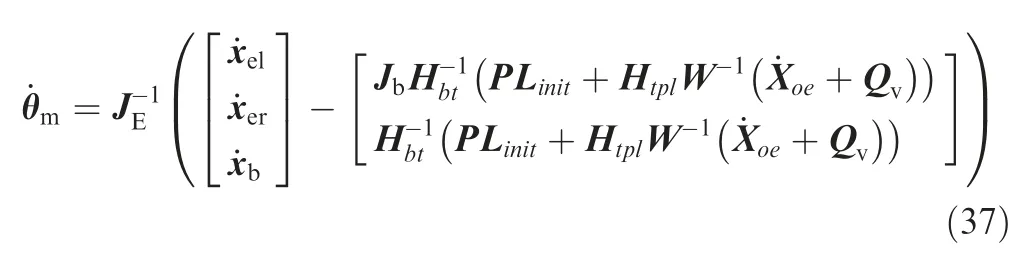
The equations of motion of the base and the generalized Jacobian matrix are combined to obtain the extended Jacobian matrix,thus the coordinated planning of the base and the arms can be realized. To achieve base undisturbed planning, we set=0

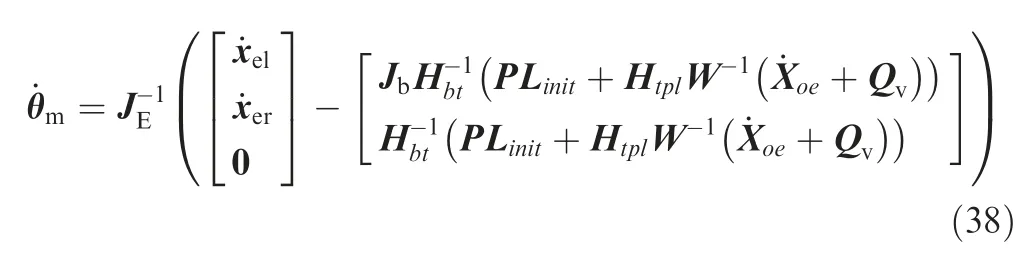
In summary, the detumbling strategy of dual-arm space robot considering base attitude stabilization is designed in this section.In Section 3.1,the multi-space hybrid impedance control method is adopted to achieve a precise friction control,which can reduce the target angular velocity steadily. In Section 3.2, the dual-arm extended Jacobian matrix is designed to stabilize the base attitude without affecting the target capture task. The dual-arm extended Jacobian matrix not only includes kinematic parameters, but also includes the dynamic parameters,as well as the base parameters and target parameters. In addition, the detumbling strategy fully considers the coupling relationship between the base and the arms,and realizes their coordinated planning during the tumbling target capture process.

The proposed strategy structure is shown in Fig. 7.

4. Simulation

In this section, the simulation is carried out to verify the proposed detumbling strategy. The task schematic is shown in Fig. 8.

The robotic system is a dual-arm space robot with two 7-DOF arms.The D-H frames and D-H parameters of the robot are listed in Appendix A.The target is a cylinder,whose radius rois 0.2 m,height is 0.25 m,mass mois 250 kg,and stiffness kois 1000 N/m. The rotation status of tumbling target is set to ωo=20 (°)/s.

4.1. Simulation settings

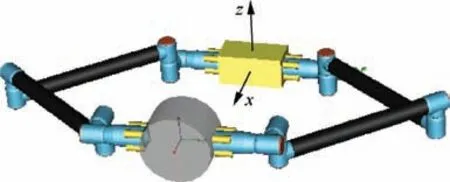
Fig. 8 Task schematic of dual-arm space robot detumbling tumbling target.

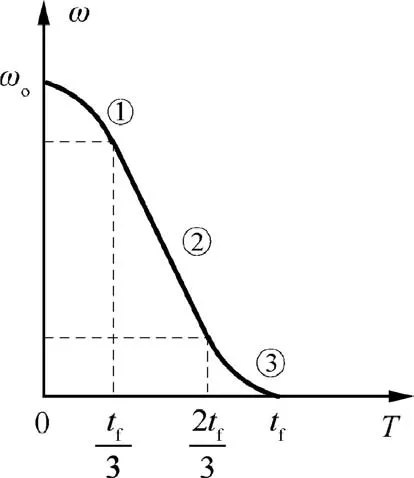
Fig. 9 Deceleration planning with arc transition.

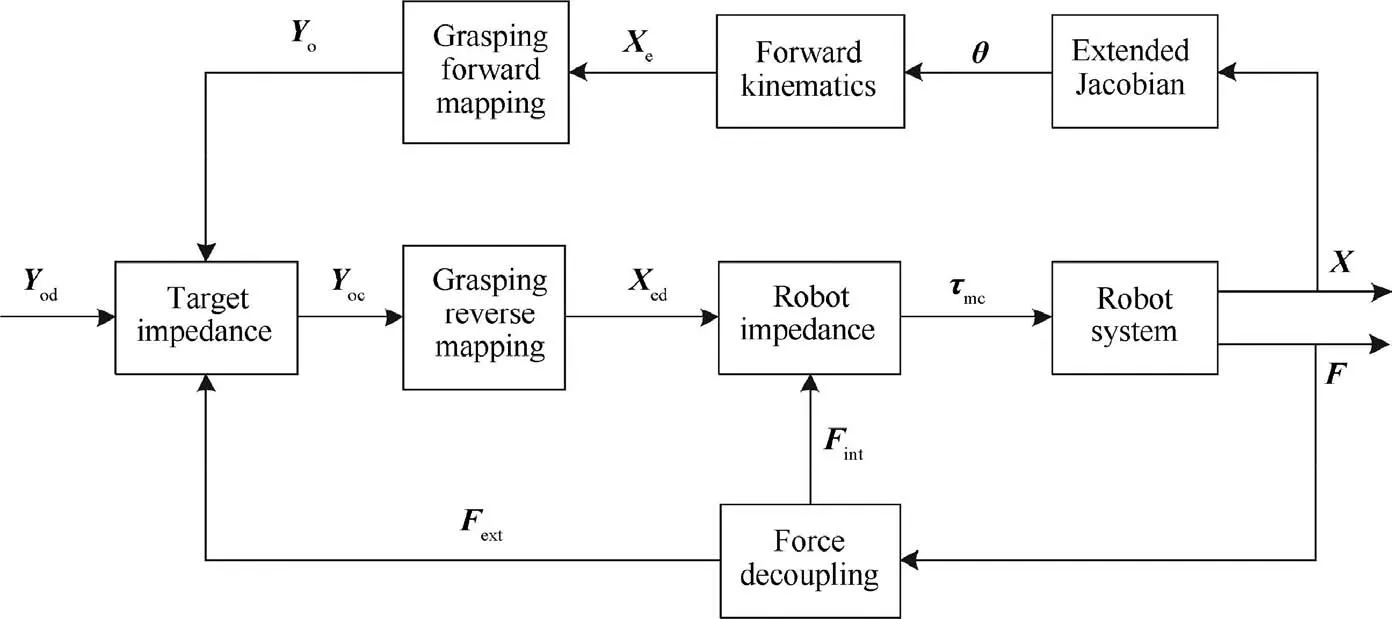
Fig. 7 Detumbling strategy structure of the dual-arm space robot.

Table 2 Two sets of simulation parameters.

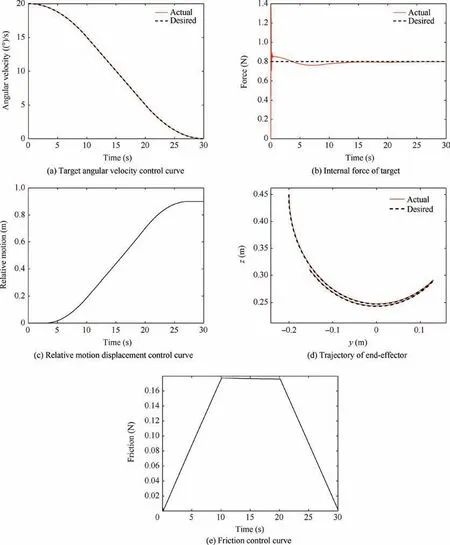
Fig. 10 Control curve of the rotation attenuation controller verification simulation.

In order to reflect the controllable characteristics of the target motion, the desired angular velocity trajectory of target is designed as deceleration planning mode with arc transition(Fig. 9). The initial joint of robot is set as θini=[-90°,0°,40°,100°,-140°,

180°,0°,90°,0°,-40°,-100°,140°,180°,0°]T. The total control time tfis set as 30 s.

We verify the effectiveness of the proposed detumbling strategy from two aspects: 1) whether it can reduce the target angular velocity steadily; 2) whether it can stabilize the base attitude while reducing the velocity.

Two sets of simulation parameters settings are shown in Table 2.

4.2. Simulation results

4.2.1. Verification of the rotation attenuation controller

By using the multi-space hybrid impedance method,the results shown in Fig. 10 are obtained. Fig. 10(a) is the target angular velocity control curve,Fig.10(b)is the internal force of target,Fig. 10(c) is the relative motion displacement control curve,Fig.10(d)is the trajectory of end-effector,Fig.10(e)is the friction control curve.

Fig. 10(a) shows that the target’s angular velocity can be tracked precisely. The final internal force tracking error is maintained within 10-5N (Fig. 10(b)).

Fig. 10(c) shows that the end-effector slides about 0.88 m along the target surface, but as can be seen from Fig. 10(d),the end-effector actually only turns about 0.17 m with respect to the inertial frame. This is because the rotation attenuation process is completed by using the sliding friction force generated by the relative motion. In this way, the displacement of the end-effector can be greatly decreased, and the probability of dynamic singularity and interference between the arms can be reduced.

Fig.10(e)shows the actual friction force corresponds to the acceleration trapezoidal curve of the target strictly.

From the simulation results, the multi-space hybrid impedance control method can achieve the precise friction control.Thereby the target angular velocity can be steadily reduced.In addition, by using the sliding friction force, the end-effector only needs to move 0.17 m with respect to the inertial frame,and the range of motion is greatly reduced, which guarantees the reliability of the capture process.

4.2.2. Verification of the base attitude adjustment controller

By using the proposed dual-arm extended Jacobian matrix,the results are obtained, as shown in Fig. 11. Fig. 11(a) is the target angular velocity control curve, Fig. 11(b) is the internal force of target. Before applying the base attitude adjustment controller, the base attitude control curve is shown in Fig. 11(c). After applying the base attitude adjustment controller,the base attitude control curve is shown in Fig. 11(d).

Fig. 11(a) shows that the target’s angular velocity can be tracked precisely.The final internal force tracking error is maintained within 10-3N(Fig.11(b)).Compared with the previous simulation,the force control accuracy is reduced by two orders of magnitude.But it also meets the control requirements.

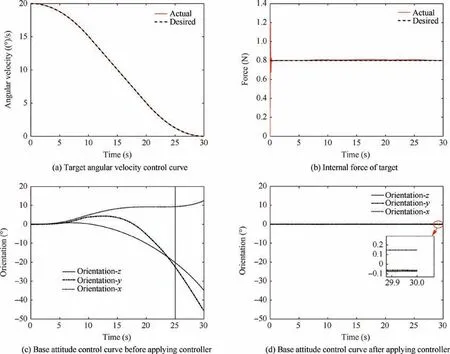
Fig. 11 Control curve of the base attitude adjustment controller verification simulation.

Fig.11(c)shows the final deflection of the base is up to 45°if no base attitude adjustment controller is applied. After applying the base attitude adjustment controller, the final deflection of the base reduced to 0.15° for the same capture task, as shown in Fig. 11(d).

From the simulation results, the base attitude adjustment controller based on the extended Jacobian matrix can stabilize the base attitude without affecting the target capture task.Compared to the 45° deflection in the previous simulation,the 0.15° deflection is almost negligible, which means that the controller can effectively reduce undesired base interference.

4.3. Results analysis

Section 4 takes a specific dual-arm space robot as an example,and the proposed detumbling strategy considering base attitude stabilization is applied to the robot. It can be seen from Section 4.2.1 that the actual friction force corresponds to the acceleration trapezoidal curve of the target strictly (Fig. 10(e)). The target’s angular velocity can be tracked precisely(Fig.10(a)).And the final internal force tracking error is maintained within 10-5N (Fig. 10(b)). These results indicate that the rotation attenuation controller achieves the precise friction control,realizes the stable tracking of the desired movement of the target, and ensures the compliance between the endeffectors and the target. It can be seen from Section 4.2.1 that the target’s angular velocity can be tracked precisely (Fig. 11(a)) and the final internal force tracking error is maintained within 10-3N (Fig. 11(b)). At the same time, the final deflection of the base reduced to 0.15° for the same capture task(Fig. 11(d)). These results indicate that the base attitude adjustment controller can stabilize the base attitude without affecting the target capture task. The simulation results and analysis in Section 4.2 prove the effectiveness of the strategy.It means that this paper provides a viable solution for the dual-arm space robot to capture the tumbling target.

5. Conclusions

Aiming at capturing a tumbling target by a dual-arm space robot, a detumbling strategy based on friction control is proposed in this paper. First, the multi-space hybrid impedance control method is adopted to achieve the precise friction control, thereby reducing the target angular velocity steadily.Based on it, the dual-arm extended Jacobian matrix is used to stabilize the base attitude. The coordinated planning of the base and two arms can be realized concisely,and base attitude stability can be achieved without affecting the target capture task. Therefore, we can reduce the tumbling target’s rotational velocity steadily under the premise of ensuring the base attitude stability.To validate the strategy,two sets of simulation are carried out on a dual-arm space robot with two 7-DOF arms. The correctness and effectiveness of the proposed strategy are verified by the simulation.

The main contributions of this paper are as follows:

(1) The multi-space hybrid impedance control method is adopted to achieve a precise friction control, which can reduce the target angular velocity steadily.

(2) The dual-arm extended Jacobian matrix is applied to stabilize the base attitude without affecting the target capture task. This method can be apply to any redundant arms and can generate smooth joint motion.

(3) The detumbling strategy of dual-arm space robot is designed considering base attitude stabilization, to achieve the smooth capture of the tumbling target. In addition, this strategy fully considers the coupling relationships between the base and the arms, and realizes their coordinated planning during the tumbling target capture process.

Except to the tumbling target capture task, the control strategy can also be applied to other typical on-orbit operation tasks such as space debris removal and spacecraft maintenance. Considering that the control strategy in this paper is aimed at the rigid robot,flexible robot is an option for further study.Besides,the unknown dynamic characteristic of the target is also a research direction.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China (Nos. 61403038 and 61573066) and the Open Research Fund of Key Laboratory of Space Utilization,Chinese Academy of Sciences(Nos.LSU-2016-05-2 and LSUKJTS-2017-02).

Appendix A

The robotic system is a dual-arm space robot with two 7-DOF arms.The joint frames of the robot are created according to DH method and the D-H frames and D-H parameters are listed in Fig. A1 and Table A1.

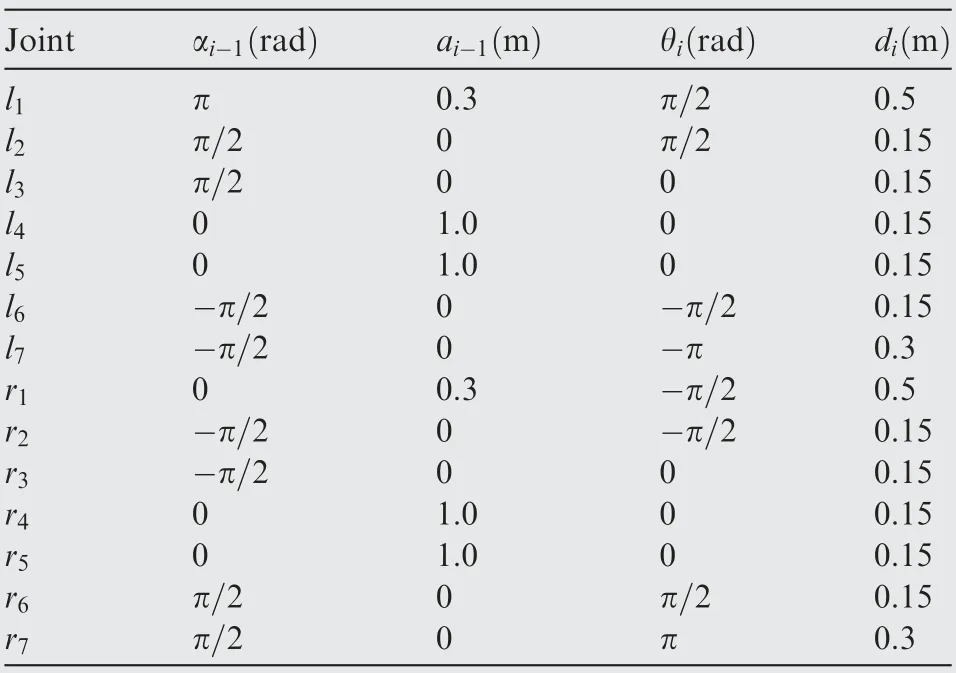
Table A1 D-H parameters of the robot in simulation.