Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation
Kepeng QIU, Ruoyao WANG, Jihong ZHU, Weihong ZHANG
School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China
KEYWORDS Chiral hexagonal honeycombs;Genetic algorithm;Geometric nonlinearity;Large deformation;Shape optimization
Abstract Flexible chiral honeycomb cores generally exhibit nonlinear elastic properties due to large geometric deformation. The effective elastic moduli and Poisson’s ratio typically vary with an increase in deformation. Here, the size and shape optimization of the chiral hexagonal honeycombs was performed to keep the Young’s moduli and Poisson’s ratio unchanged under large deformations. The size of the honeycomb unit cell and the position coordinates of the key points were defined simultaneously as design variables. The equivalent Young’s modulus and Poisson’s ratio of chiral honeycombs were calculated through geometric nonlinear analysis. The objective was to minimize the allowable tolerance between the prescribed and actual properties within the range of the target strain. A genetic algorithm was then adopted. The optimal results demonstrate that the chiral honeycombs can maintain effective elastic properties that do not vary under large deformation. These results are meaningful to morphing aircraft designs.
1. Introduction
Chiral hexagonal honeycombs exhibit a geometric feature of in-plane hexagonal symmetry,whereby circular nodes are connected through six ligaments tangent to the nodes themselves that produce a negative Poisson’s ratio (auxetic) response in-plane.1,2As a special type of cellular material,chiral honeycombs are particularly well suited for lightweight morphing aircraft structures due to their high stiffness-to-weight ratio and designable nonlinear features.3They also have low inplane stiffness and high out-plane flexural bending stiffness,which attract the attention of researchers of in-plane and out-plane mechanical properties with special configurations.4,5Mousanezhad et al.6used the energy-based approach to calculate the elastic moduli of chiral honeycombs, demonstrating that introducing chirality decreases the in-plane stiffness of hexagon-based honeycombs, which remains the only route to auxeticity. The out-plane strength of chiral honeycombs is investigated through analytical formulas, finite element methods and experimental tests.7,8The circular nodes provide the majority of the compressive strength of the honeycombs under uniform axial loading. The flat-wise performance can be improved by modifying the geometric parameters of the chiral honeycombs. Lorato et al.9identified that the out-plane compressive and shear strengths are partially decoupled between the cylinders and ligaments,and the higher connectivity honeycombs offer superior transverse shear modulus responses than the lower connectivity honeycombs. The study of Miller et al.10demonstrated that the chiral geometry does provide an improvement in buckling strength due to the connectivity of the cylinders and ribs although the negative Poisson’s ratio is not directly responsible for the improved buckling strength. Using both experimental and theoretical analysis, Hu et al.11found that the crushing stress of chiral honeycombs under lateral loading decreases with the ligament length ratio, L/r.
For flexible honeycomb structures, geometrically non-linear deformation is particularly important due to the generally larger deformation of the cell structures. Compliant cellular materials have two important structural mechanisms that can be used to determine the modulus: the deformation is controllable and the stiffness is tunable.12,13In order to appropriately tailor the overall stiffness (yield strength) and flexibility (yield strain) of cellular materials, the function of each individual strut under a large deformation must be understood. Lan and Fu14built nonlinear constitutive relations of cellular materials based on the elastic bending theory of beams under large deflection.The nonlinear shear modulus of the reentrant hexagonal honeycombs under large deformation was analytically derived by Fu et al.15Therefore, the elastic properties of cellular materials under large deformation can be designed. The Poisson’s ratio of the chiral three-dimensional lattices can be tuned to negative values by specific geometries.16
Cellular structures with chiral honeycombs can undergo large overall displacements with limited straining of its components.Such properties were exploited to design a passive morphing airfoil with flexible cellular cores.17,18Bornengo et al.19proposed a hexagonal chiral honeycomb material design that exhibited a negative Poisson’s ratio under a large range of strain, and the material was applied as a truss-like internal structure for adaptive wing box configurations. Spadoni and Ruzzene20proposed an alternative structural assembly for airfoil morphing that allows continuous conformability while maintaining load-carrying capabilities. The design requirements for adjustable wing structures and surfaces include large strains, low in-plane stiffness, and high out-plane flexural bending stiffness.21,22Airoldi et al.23,24produced chiral honeycombs made of thin composite laminates and manufactured the morphing ribs for a variable camber wing-box. Budarapu et al.25proposed a framework to design an aircraft wing structure and analyze a morphing airfoil with chiral structure. The advantages of the morphing airfoil with auxetic structure are larger displacement with limited straining of the components and unique deformation characteristics. Wang et al.26,27designed materials using topology optimization to achieve prescribed nonlinear properties. A geometrically nonlinear model was obtained and a requirement of a constant prescribed Poisson’s ratio was met when straining the material.Wang further designed 3D auxetic lattice materials that exhibit constant negative Poisson’s ratios over large strain intervals.28
Hexagonal chiral honeycombs are special materials and structures with negative Poisson’s ratio. This work aims to look into the novel chiral honeycombs with prescribed elastic modulus and Poisson’s ratio using the size and shape optimization under large deformation. These new chiral honeycombs were fabricated using a commercially available 3D printer and the optimal results were verified experimentally.The optimal results reveal that the nonlinearity of the chiral hexagonal honeycombs directly affects the effective elastic properties.The rest of this paper is organized as follows.Section 2 presents the computations of effective elastic moduli and Poisson’s ratio of chiral hexagonal honeycomb under the finite strain. Section 3 first presents the optimal formulation for the prescribed properties; then, optimization designs with the prescribed Young’s moduli and Poisson’s ratio are executed. The optimal models are fabricated and the results are verified experimentally. In Section 4, conclusions are given.
2. Chiral hexagonal honeycomb with changing elastic properties
As shown in Fig. 1, the chiral honeycomb structure is composed of circular elements (nodes) of equal radius joined by straight ligaments that are tangent to the nodes. The in-plane deformation mechanism of the honeycomb is provided by the rotation of the nodes, which leads to bending and axial deformation of the attached ligaments. The ligaments of the chiral honeycomb form an S-shape under in-plane uniaxial loading along two orthogonal directions.
The initial size parameters of the hexagonal chiral honeycomb were defined as a circular radius of r=5 mm, wall thickness of t=1 mm,and distance between the circle centers of R=30 mm. The Young’s modulus of the honeycomb wall is Es=90 GPa and the Poisson’s ratio is vs=0.3.
For computation of the Young’s modulus,29as shown in Fig.2,the chiral hexagonal honeycomb was subject to uniform displacement in the y-axis direction. The force required to cause this displacement was calculated from the tractions T on the boundary of a prescribed displacement condition, that is

where Γdrepresents the boundary with prescribed uniform displacement,S represents length(2D)or area(3D).Based on this force,the effective Young’s modulus Eyof the chiral hexagonal honeycomb was calculated through a straightforward analysis
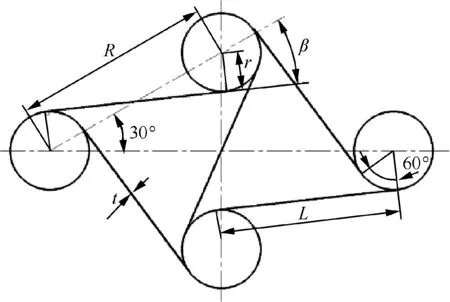
Fig. 1 Schematic of chiral honeycomb core with six ligaments.
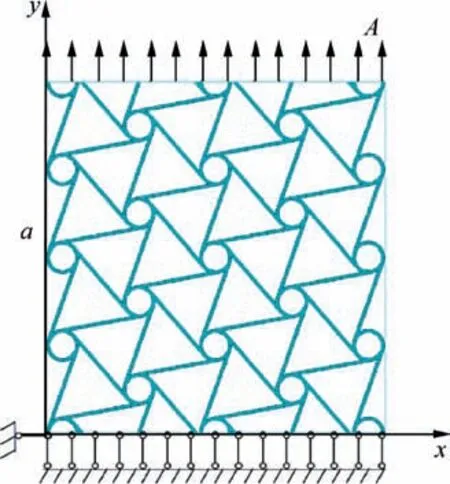
Fig. 2 Model for numerical computation of effective Young’s modulus.

where A represents the section area of the structure boundary on which a uniform displacement u is applied, and a is the length of the chiral hexagonal honeycomb along the y-axis direction.Additionally,the same analysis can be used to calculate Ex,which is equal to Eybecause the chiral hexagonal honeycomb is centrosymmetric.
The chiral hexagonal honeycomb has a large length to thickness ratio. This results in generally large deformation of the cell structures, and thus the geometrically nonlinear deformation is particularly prominent. Therefore, the effects of large deformations must be considered to more accurately evaluate the equivalent properties of flexible honeycomb materials. During the solving process using a nonlinear finite element method, the external loads are applied step by step. As shown in Fig. 3, the stress-strain relative curve is obtained under the uniaxial tensile load.
Here, we define the ratio of stress and strain in each load step as the effective stiffness of the structure as follows,

Fig. 3 Nonlinear stress-strain curve.
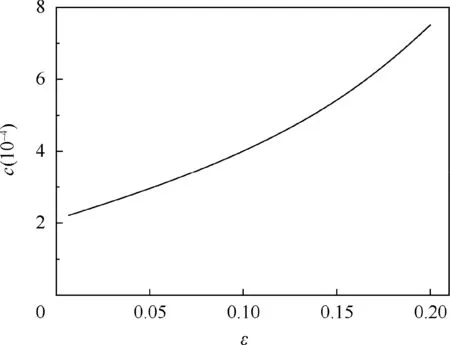
Fig. 4 Changing effective Young’s moduli under finite strain.
Assuming c=Ei/Es, where Esis the Young’s modulus of the chiral honeycomb wall. The relative effective Young’s moduli of the chiral hexagonal honeycomb change under the finite strain as shown in Fig. 4.
The effective Poisson’s ratio of the chiral hexagonal honeycombs is defined by the negative ratio of the longitude and transverse strain under each uniaxial tensile strain status as follows,

The effective Poisson’s ratio is changing for the chiral hexagonal honeycomb under the finite strain as shown in Fig. 5.
By the uniaxial tension, the effective elastic properties of the chiral hexagonal honeycomb are changing under the finite strain as shown in Figs. 4 and 5. The flexible characteristics result in the material nonlinearity.The effective Young’s moduli are increasing and the negative Poisson’s ratio effects are diminished while the tensile deformation of the chiral hexagonal honeycomb increases.This explains that not only the initial configuration, but also the deformation process, determines the effective elastic properties of the chiral hexagonal honeycomb. When the chiral hexagonal honeycomb is used for a flexible skin structure, the effective stiffness is low and unchanged under the finite deformations.
This paper aims to design chiral honeycombs with constant effective Young’s moduli and Poisson’s ratios by optimizing the size and shape using tensile tests under finite deformations.
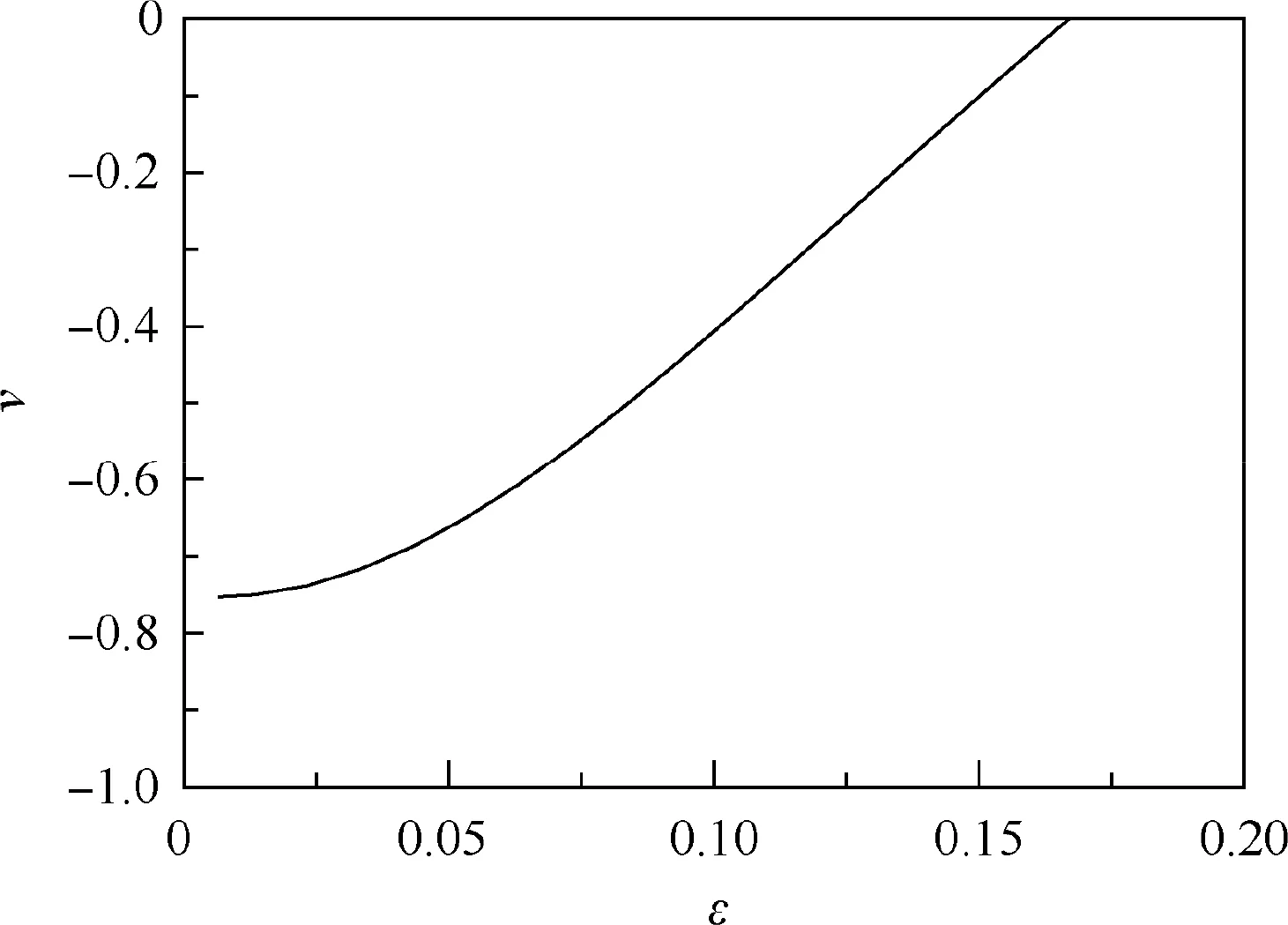
Fig. 5 Changing effective Poisson’s ratio under finite strain.
3. Optimization design of a chiral honeycomb for constant elastic properties
3.1. Optimal formulation
Structural optimization contains three branches: size optimization, shape optimization and topology optimization.Given the chiral honeycomb configuration, the size and shape optimization designs are implemented to obtain constant elastic properties.
Assuming that the size and shape design parameters are defined as design variables and the n variables are represented by the vector x, the optimal formulation of chiral hexagonal honeycombs can be expressed as follows,
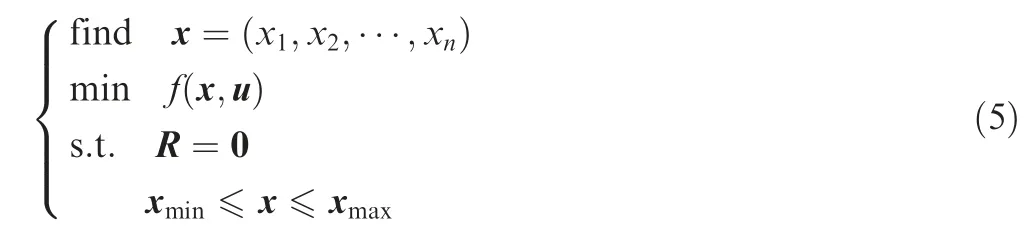
where R represents the residual in obtaining the structural equilibrium during the nonlinear finite element analysis process, xminand xmaxare, respectively, the lower and upper bounds of design variables, and u is the displacement vector.The nonlinear equilibrium equation was solved by the step iterative method. The equilibrium R=0 must appear in the iterative procedure,where R=fext-fint,fextis the external force,and fintis the internal node force.
As shown in Fig. 6, the unit cell of the chiral hexagonal honeycombs was composed of circular elements (nodes) of equal radius joined by straight ligaments. The shape of chiral honeycombs can be described by the key points and geometrical sizes.We can define the coordinates of key points and geometrical size as design variables. The line ABC is half of the ligament. For the unit cell, we define four design variables to describe the size and shape of chiral hexagonal honeycombs:the circular radius r, the thickness t of the ligament and circular,the coordinate offset d of key Point B,and the dip angle χ of the slope at Point C.Therefore,we define the variable vector x= [r t d χ]T. The new outlines of ligaments are determined through the spline interpolation by use of the ANSYS command BSPLIN according to the offset of the key Point B and the slope at Point C.
According to the offset at B and the slope at the C,we can obtain the ligament profile by the spline curve interpolation of the A, B and C points. Combining with the thickness t and radius r of the circular form, we can completely determine the configuration of the chiral hexagonal honeycomb.
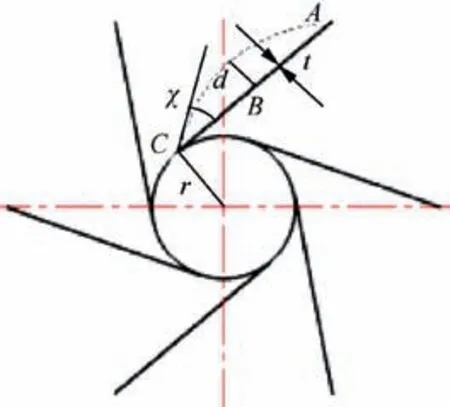
Fig. 6 Design model.
In order to keep the prescribed stiffness under the finite deformation, the specific configuration of the chiral honeycomb is obtained by the structural optimization.The optimization problem can be formulated to minimize the errors between actual and prescribed properties for a given strain range as follows,

where εi∈[ε0, ε1]is the target strain range,c(εi)and c*(εi)are the actual and prescribed properties for a given target strain εi,and m is the total number of target strains.
To implement the process,the problem is simplified and this paper only considers the material design under the tensile test.
3.2. Optimal chiral honeycombs with the prescribed Young’s moduli
Here,assuming that the relative actual and prescribed Young’s moduli are respectively c(εi)=E-(εi)×104/Esand c*(εi)=E*×104/Es, we designed the chiral honeycomb with the prescribed Young’s moduli in the strain range. The optimization formulation is,
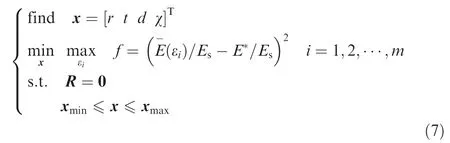
where E*is the prescribed Young’s modulus and E-(εi) is the actual Young’s modulus under the strain εi.
In this work, genetic algorithms are used as the search and optimization tools.GAs employ a random,yet directed,search for locating the globally optimal solution.The population size,crossover probability, and mutation probability were selected as 30, 0.9 and 0.25, respectively. The target stain range is εi=[0, 0.2]. The upper and lower bounds of the design variables are xmin= [2 1 0 0]Tand xmax= [8 2 1 6]T.The initial model is given in Section 2.
(1) Case 1: E*×104/Es=1.0
The chiral honeycomb when the optimal objective value E*×104/Esis 1.0 is shown as Fig. 7. The optimal variables are x= [7.85 1.0 1.0 6.0]T. The effective relative Young’s moduli vary from 1.52 to 1.85 and the average value was 1.685. The change rate was within ±9.8%. The experimental Young’s moduli varied from 1.57 to 1.46. The average was 1.515.The change rate was within±3.6%.The optimal values were close to the experimental values, although they were greater than the objective value. However, the change ranges of the Young’s moduli were low. The iteration process is convergent as shown in Fig. 8, which is similar to other cases.
(2) Case 2: E*×104/Es=3.0

Fig. 7 Optimal chiral honeycomb when E*×104/Es =1.0.
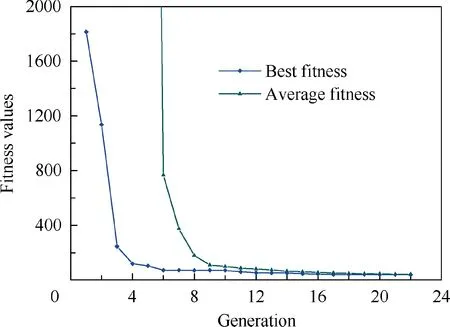
Fig. 8 Convergent process of optimization for Case 1.
The chiral honeycomb when the optimal objective value E*×104/Esis 3.0 is shown as Fig. 9. The optimal variables are x= [7.99 1.2 1.0 6.0]T. The effective relative Young’s moduli varied from 2.7 to 3.26 and the average value was 2.98.The change rate was within ±9.4%. The experimental effective Young’s moduli varied from 2.94 to 3.16. The average value was 3.05. The change rate was within ±3.6%. In this case, the optimal values were very close to the experimental and objective values. In addition, the new chiral honeycomb has a nearly constant Young’s moduli under the finite strain.
(3) Case 3: E*×104/Es=5.0
The chiral honeycomb when the optimal objective value E*×104/Esis 5.0 is shown as Fig. 10. The optimal variables are x= [7.99 1.37 0.74 5.91]T. The effective relative Young’s moduli vary from 4.41 to 5.41 and the average value was 4.91.The change rate was within ±5.0%. The experimental effective Young’s moduli varied from 5.32 to 4.54. The average value was 4.93.The change rate was within±5.0%.As in Case 2, the optimal values were very close to the experimental and objective values. In addition, they have the same low change rate of the effective Young’s moduli.

Fig. 9 Optimal chiral honeycomb when E*×104/Es =3.0.

Fig. 10 Optimal chiral honeycomb when E*×104/Es =5.0.
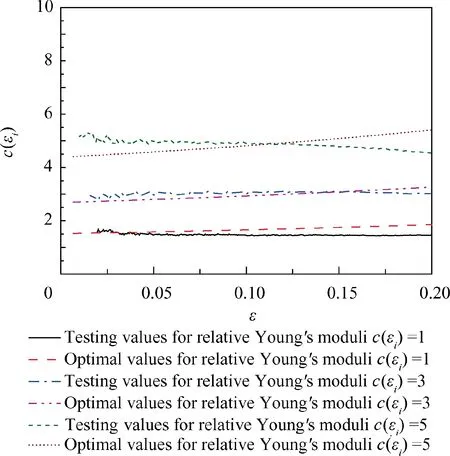
Fig. 11 Change curves of relative Young’s moduli under finite strain.
Based on these three cases, the optimal chiral honeycombs have nearly constant Young’s moduli under the finite strain as shown in Fig.11.The optimal results were verified by the tensile test demonstrating that the flexible chiral honeycombs obtained by size and shape optimization can maintain constant elastic properties under large deformation.In Case 1,the optimal and experimental average values are 1.685 and 1.515,respectively, which are greater than the objective value 1.0.For the other two cases, the objective values are very near to the optimal and experimental averages. That is because the first case has stronger nonlinearity. During the optimization process, the effective stiffness gradually becomes larger in order to keep the Young’s moduli constant.From the optimal results of three cases, we can see that the relative Young’s moduli slightly increased with the increasing finite strain under the condition of keeping the Young’s moduli nearly constant.This indicates that the effective stiffness of cellular materials depends on their nonlinearity. Considering the experimental condition and the model process, the experimental results demonstrate that the optimal chiral hexagonal honeycombs have a constant Young’s moduli.
3.3. Optimal chiral honeycombs with the prescribed Poisson’s ratio
Similarly, assuming that the actual and prescribed Poisson’s ratios are respectively c(εi)= ν-(εi)and c*(εi)=ν*,we designed the chiral honeycomb with prescribed Poisson’s ratio under the finite strain range. The optimization formulation is,
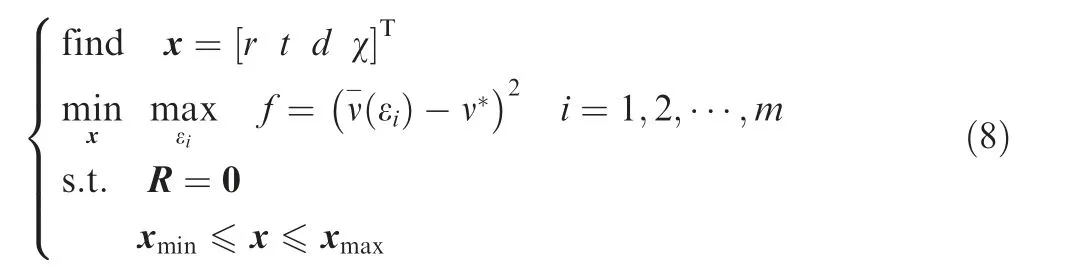

Fig. 12 Optimal chiral honeycomb when v* =-0.5.
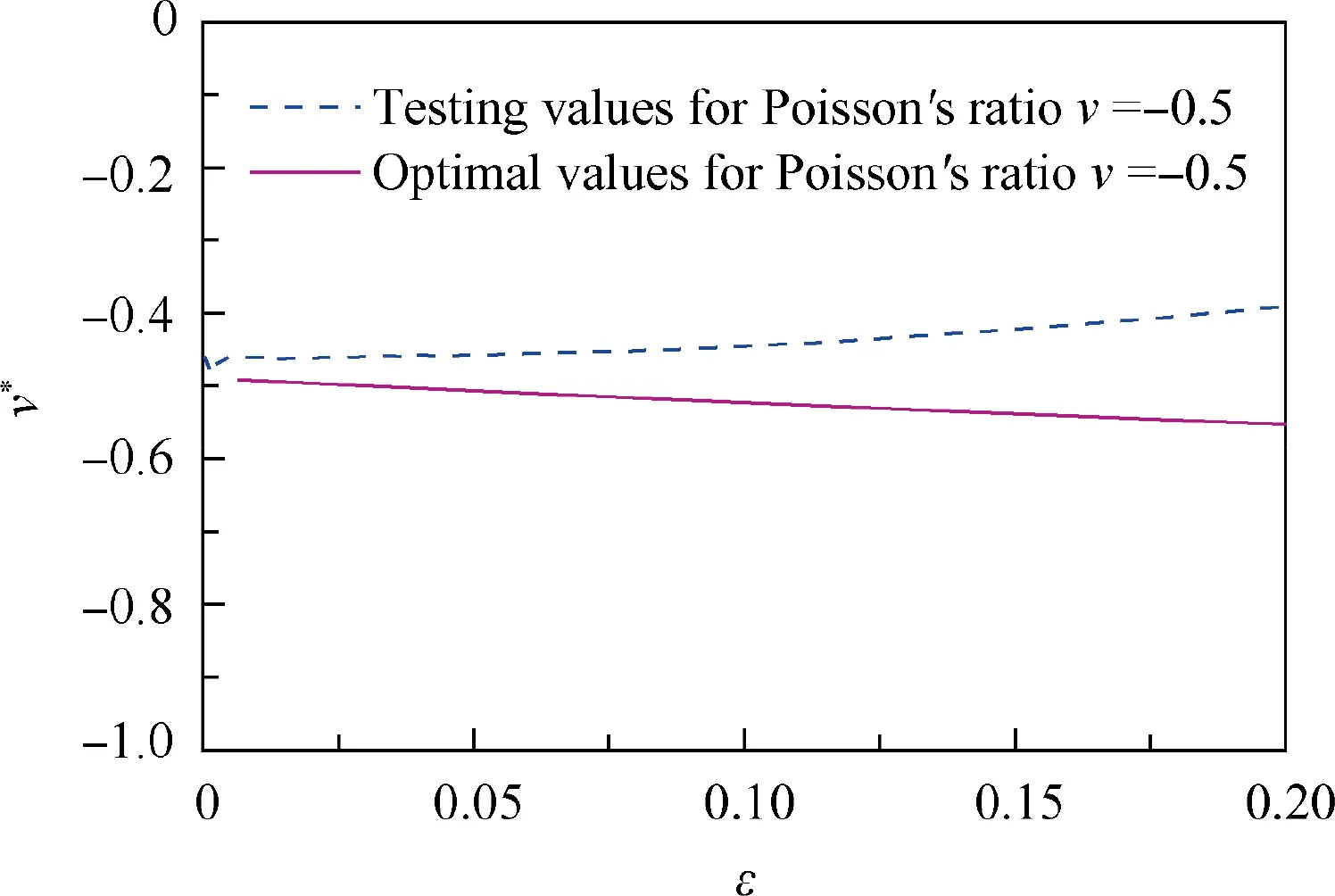
Fig. 13 Change curves of relative Poisson’s ratio under finite strain.
where v*is the prescribed Poisson’s ratio and v-(εi)is the actual Poisson’s ratio under the strain εi. In the same way, genetic algorithms were used as the search and optimization tools.The population size, the crossover probability, and the mutation probability were respectively selected as 30, 0.9 and 0.25. The target stain range was εi=[0, 0.2]. The upper and lower bounds of design variables were xmin= [2 1 0 0]Tand xmax= [8 2 1 6]T.
The chiral honeycomb when the optimal objective value v*is -0.5 is shown as Fig. 12. The optimal variables are x= [4.59 1.97 0.03 5.98]T.The effective Poisson’s ratios varied from -0.49 to -0.55. The average Poisson’s ratio was-0.52. The change rate was within ±5.8%. The experimental Poisson’s ratios varied from-0.39 to-0.46.The average value was -0.43. The change rate was within ±8.2%. The optimal values were larger than the experimental but were close to the objective value. Both of which had low effective Poisson’s ratio change rates.
As shown in Fig. 13, the optimal chiral honeycombs have nearly constant Poisson’s ratios under the finite strain.The effective Poisson’s ratios obtained by the tensile test were nearly constant. The optimal values and testing values all approached the targeted Poisson’s ratio although they have a small deviation.These demonstrate that the flexible chiral honeycombs can be tuned by the size and shape optimization method to maintain a constant Poisson’s ratio under large deformation. Similar to the optimal examples with the prescribed Young’s moduli,the effective Poisson’s ratio gradually becomes lower with increasing finite strain.This shows that the effective Poisson’s ratio depends on its nonlinearity.When the nonlinearity is stronger, Poisson’s ratio is more negative.Because the experimental material is the epoxy resin, the testing value is larger than optima by consideration of the model process. However, the experiments still demonstrate that the novel chiral honeycombs possess a constant Poisson’s ratio under the finite strain.
4. Conclusions
In this paper,chiral honeycombs were designed by the size and shape optimization method to keep a constant Young’s moduli and Poisson’s ratio under large deformations. The optimal models were fabricated by 3D printing and the optimal results were verified by tensile tests. The optimal results also demonstrate that the invariance of the effective elastic properties depends on the nonlinearity of the flexible chiral hexagonal honeycombs. The invariability of the effective elastic properties is lower;the nonlinearity of the chiral hexagonal honeycombs is stronger.
In addition, this study shows that the flexible chiral honeycombs have very strong designability. When the chiral honeycombs are used in morphing aircraft, the structural strength can be guaranteed while meeting the deformation requirements.
Acknowledgements
This work is supported by National Key Research and Development Program (2017YFB1102800), NSFC for Excellent Young Scholars (11722219), National Natural Science Foundation of China (11772258, 51790171, 5171101743).
 CHINESE JOURNAL OF AERONAUTICS2020年3期
CHINESE JOURNAL OF AERONAUTICS2020年3期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Experimental investigation on operating behaviors of loop heat pipe with thermoelectric cooler under acceleration conditions
- Investigation of hot jet on active control of oblique detonation waves
- Experimental study of rotor blades vibration and noise in multistage high pressure compressor and their relevance
- Unsteady wakes-secondary flow interactions in a high-lift low-pressure turbine cascade
- Effect of protrusion amount on gas ingestion of radial rim seal
- A global solution for robust parameter design of aeronautical electrical apparatus based oninteractions analysis and polynomial fitting
