Adaptive controller design for satellite attached by non-cooperative object
Guohu KANG, Jiqi WU, Chendi JIN, Xuefen CHEN
a College of Astronautics, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China
b Nanjing Changfeng Aerospace Electronic Technology Co. Ltd, Nanjing 210013, China
KEYWORDS Adaptive control scheme;Inertia estimation;New combination;Non-cooperative body attachment;Robustness
Abstract When non-cooperative body attachment occurs in space,the inertia of the new combination and the change of the system’s momentum are unknown. This uncertainty may lead to the instability of the spacecraft’s attitude control.In order to solve this problem, we propose an adaptive control scheme based on the inertia estimation of the new,combined system of non-cooperative body and satellite. This method can allow the new combination of different situations to reach a stable state with a high level of precision and speed.In this paper,the stability of the adaptive control scheme is proven by constructing a Lyapunov function. A simulation environment in which a non-cooperative body attaches to a satellite attaches to is constructed. The simulation shows that the attitude error converges to a small field when using the control scheme, regardless of unfavorable cases, including unknown inertia parameters, added momentum. In addition, the simulation results show the strong robustness of the control scheme for the new combination.
1. Introduction
In real space applications and space combat,spacecraft attachment issues are frequent problems, as mentioned by Hollander1and Ross et al.2The attached spacecraft can be either a cooperative or non-cooperative target. If a non-cooperative target body attachment happens, the full impact that might be felt on the target spacecraft’s attitude control must be considered. The target spacecraft should have the ability to quickly restore the original attitude.
Non-cooperative attachment, as it is studied in this paper,refers mainly to cases of unknown outline dimensions,unknown centroid position, and unknown movement spacecraft attachment(including a variety of docking methods,such as mechanical capture and adhesion). Tarabini et al.3and other scholars all believe that when an object with a particular mass and momentum attaches to the target body,the centroid position and the inertia parameters are changed. Attitude disturbance also occurs. Eliminating and preventing the attitude disturbance brought about by the non-cooperative attachment,whether intentionally or unintentionally, is an emerging issue for non-cooperative combination attitude control in future space applications.
In recent years, several studies have focused on attitude control for non-cooperative combinations. Many scholars have suggested some control strategies for difficult cases in which inertia matrix or external disturbance are uncertain.Among them,some have tried the fuzzy-PD or the gain scheduled PD. Both of the two methods have been studied by too many scholars. For example, Moradi4focused only on how to meet the system response speed in some cases, regardless of figuring out the specific unknown parameters. For the new combination system, however, unknown parameters such as the inertia should raise concerns.There are also some scholars who care about parameter uncertainty.For example,Song et al.5studied the design of nonlinear robust decentralized controllers for spacecraft, subject to external disturbance and uncertainty in the parameters of inertia. In light of the thrust misalignment of the chaser spacecraft, an integrated robust adaptive controller for 6 DOF (Degree of Freedom) relative motion was designed. Sun and Huo6presented a novel adaptive attitude control scheme for spacecraft with inertia matrix parameters with both unknown rigid components and only partially determined variable components. The proposed controller directly compensates for inertia variations that occur as either pure functions of the control input, or as functions of time. A neural network-based adaptive attitude tracking controller was developed in Thakur et al.7, achieving attitude tracking in the presence of parametric uncertainty, nonlinear actuator disturbances,and unmolded external disturbance torques. Wei et al.8investigated a novel learning-based adaptive takeover control method, which didn’t need to identify the unknown inertial properties.All of the aforementioned studies considered the parametric uncertainty of the spacecraft and proposed a wide range of complex methods in order to compensate, and the control schemes were not easy to implement.In addition, in the case of unknown inertia matrix, many scholars have proposed the use of satellite gyroscopes,accelerometers, and other sensors to proactively identify the kinetic parameters,such as inertia,in orbit9-11.Based on orbit identification, further control schemes have been researched.However, this method of identification depends on the actuators’ repeated maneuvers to obtain multiple sets of data, and in some cases,special actuators such as the variable speed control moment gyros.12The cost of this process would be a barrier to its wider use. Some researchers also began to study the scheme which could not only control combination but also identify the unknown parameters. Wang et al.13designed an integrated control framework which includes detumbling strategy, coordination control and parameter identifications. Han et al.14proposed an integrated identification and control method, which enables the real-time parameters identification and attitude takeover control to be conducted concurrenty.Yu et al.15considered a completely non-cooperative case,which means that both orbit elements and inertial tensor of target spacecraft are unknown.
All of the aforementioned studies in the simulation considered the condition of server and target unilateral.In this paper,the attitude control system of the target spacecraft, which is attached to by a non-cooperative body, is the main focus.An easy-to-implement control theme is proposed, which can not only effectively control the new combination system under all kinds of awful cases, but also work out the unknown inertia.The adaptive control scheme used to solve the problem caused by non-cooperative attached is based on inertia estimation,and allows the new combination of different situations to reach a stable state with precision and speed.The robustness of this method of attitude control system is proven in subsequent sections of this paper.
2. Spacecraft model and non-cooperative attachment model
2.1. Spacecraft model
(1) Spacecraft attitude dynamics
The rigid spacecraft attitude dynamics equations12can be expressed as follows:

where ω ∈R3is the angular rate vector of the spacecraft body coordinate system relative to the inertial coordinate system.Lc,Ldist∈R3, respectively, are the control torque vector and interference torque vector. ω×is the skew-symmetric matrix for any ω=[ωxωyωz]T.
Given that we discuss mainly the new combination after non-cooperative attachment with many unknown parameters,the inertia matrix is assumed to be a third-order nonsymmetric matrix. Thus, the inertia matrix can be expressed as follows:

(2) Spacecraft attitude kinematics
The spacecraft attitude kinematic equations16,17described by the quaternion can be expressed as follows:

Since the target quaternion is constant, by further derivation of the error quaternion, equations can be drawn as follows:
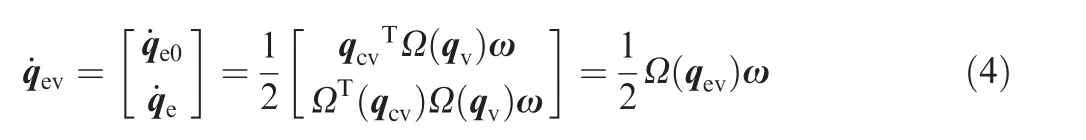
2.2. Non-cooperative attachment model
Non-cooperative attachment, as it is studied in this paper,refers mainly to cases of unknown outline dimensions,unknown centroid position,and unknown movement in spacecraft attachment.Fig.1 shows the non-cooperative attachment model. When the non-cooperative body attaches to the target spacecraft, the new, combined system is hard to control, since it would cause obvious disturbance and unknown inertia


where
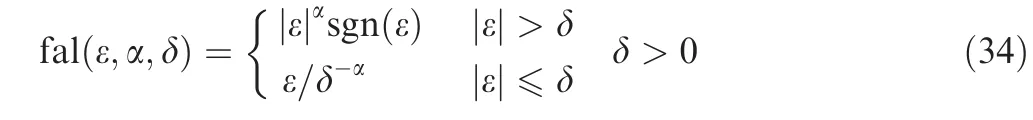
(1) Cases of 1:1 non-cooperative attachment
If the non-cooperative attachment occurred, the new system was under the scheduled PD control scheme. The control effect of the 1:1 non-cooperative attachment is shown in Fig.4.

(2) Cases of 1:1 non-cooperative attachment,carrying more momentum
The more momentum it carries,the greater disturbance that the non-cooperative body brings needed to be resisted. In this case, the simulation was carried out for a small satellite attached to by a non-cooperative body with an inertia matrix of J1.The control effect of the 1:1 non-cooperative attachment under PD control is shown in Fig. 5. Due to the increased momentum, the angular rate increased to the size as Eq. (33).
(3) Cases of 1:10 non-cooperative attachment
In this case,the simulation was carried out for a small satellite attached to by a non-cooperative body with an inertia matrix of J2. The control effect of the 1:10 non-cooperative attachment under PD control is shown in Fig. 6. Due to the increased momentum, the angular rate increased to the size as Eq. (33).
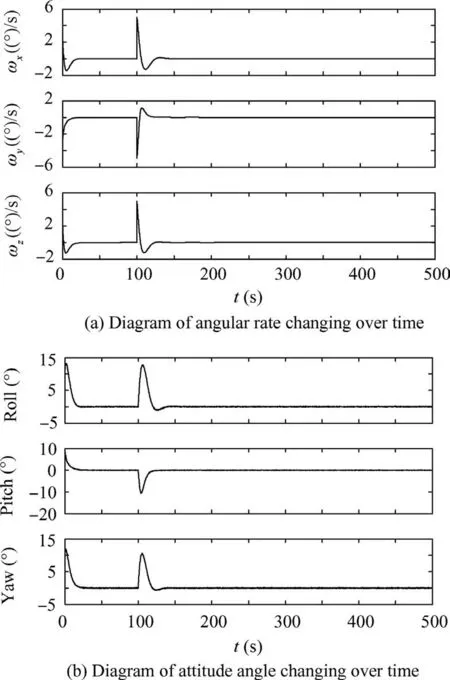
Fig. 4 Control effect of 1:1 non-cooperative attachment under gain scheduled PD control.
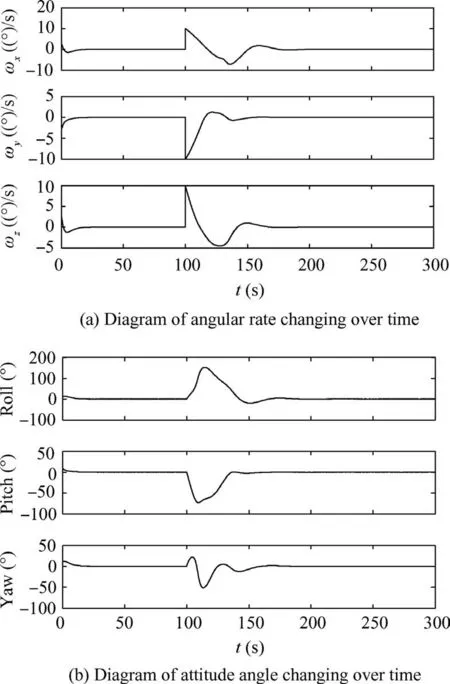
Fig.5 Control effect of 1:1 non-cooperative attachment carrying more momentum under gain scheduled PD control.
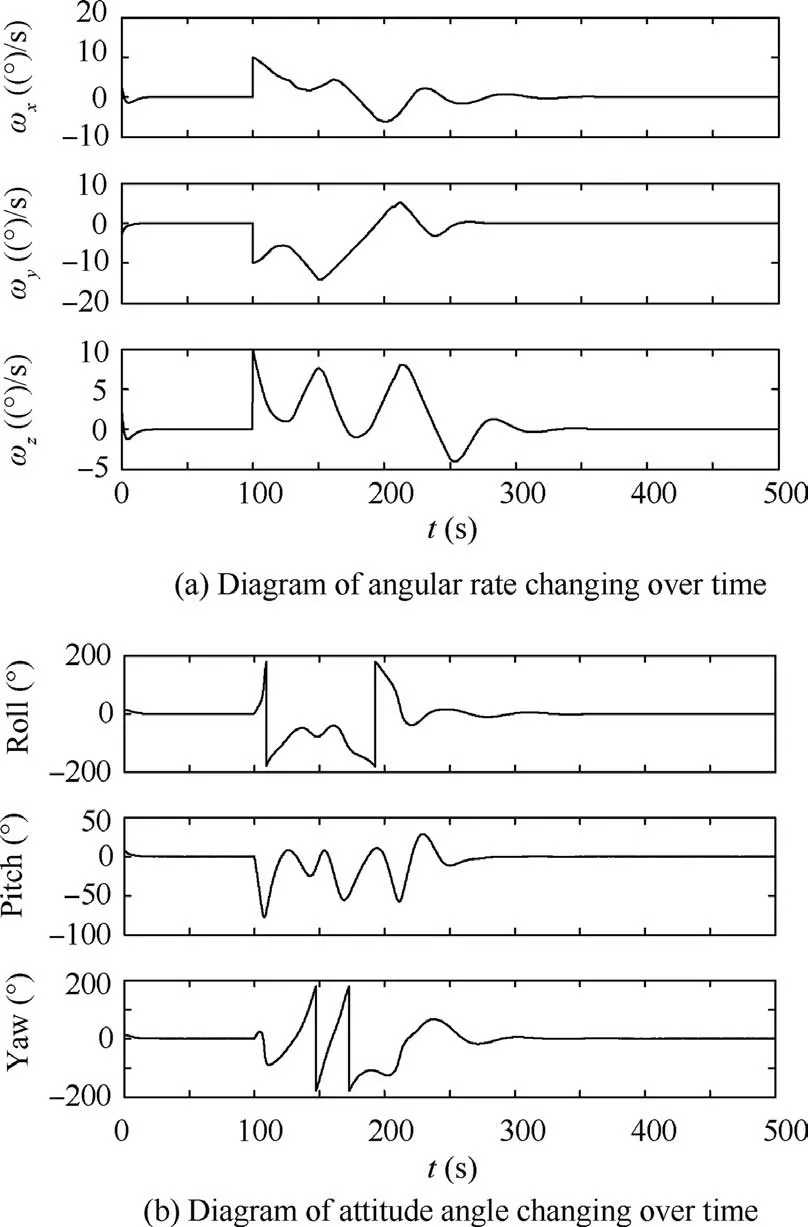
Fig. 6 Control effect of 1:10 non-cooperative attachment under gain scheduled PD control.
The control effects of the non-cooperative system under different cases are shown in Figs.4-6.Although the system could eventually return to a steady state, when more momentum is added or the size of non-cooperative object becomes bigger,the control effects become worse, especially when the latter happens. As you can see in Fig. 6, under the case of 1:10 attachment it takes about 212 s to recover. Both the angular rate and attitude angle oscillate a lot.And the oscillation range of attitude angles even reach 180°.In order to solve this problem, we have to come up with a control scheme which can be more sensitive to the change of the non-cooperative system inertia.
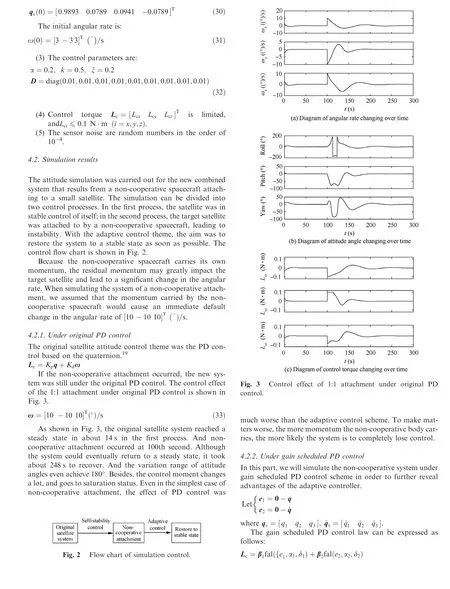
4.2.3. Under adaptive control
In this part, different cases of the system under the proposed adaptive control scheme will be simulated.
(1) Cases of 1:1 non-cooperative attachment
Non-cooperative body with an inertia matrix of J1attached to the small satellite under the proposed adaptive control is simulated. The control effect of the 1:1 attachment is shown in Fig. 7. The enlargement drawing of the steady-state behaviors are shown in the pictures, the following simulations are similar to these.
As shown in Fig. 7, it took only 15 s for the system to return back to the stable state controlled by the adaptive control theme.Compared with gain scheduled PD control schemes under the same conditions in Fig. 4 the adaptive control scheme was much more effective. Using the adaptive control scheme, the system can recover as soon as possible. These results indirectly validate the effectiveness of the proposed adaptive control scheme.
(2) Case of 1:10 non-cooperative attachment
In this case,the simulation was carried out for a small satellite attached to by a non-cooperative body with an inertia matrix of J2. The control effect of the 1:10 non-cooperative attachment under the proposed adaptive control is shown in Fig. 8. Due to the increased momentum, the angular rate increased to the size as Eq. (33).
As shown in Fig.8,even when 1:10 non-cooperative attachment occurred,the new combination system using an adaptive control scheme tended to become stable after about 79 s. As the inertia matrix was ten times bigger than the 1:1 attachment,the control time was only a little longer. Compared with the gain scheduled PD control in Fig. 6, we can easily see that,not only the control time but also the oscillation of the angular rate and attitude angle is much less.The system under the proposed adaptive control theme is more sensitive to the change of the system inertia. In fact, even when the inertia of the noncooperative spacecraft becomes 110 times larger than the original spacecraft, the system can still reach stability in about 5700 s,approximately the length of an orbital period.According to much of the research on spacecraft attitude control,control of the system within an orbital period is an acceptable result. Therefore, the control system is robust in dealing with different sizes of inertia from the non-cooperative spacecraft.
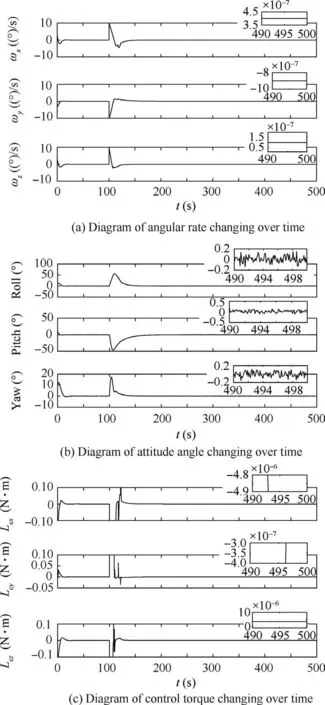
Fig. 7 Control effect of 1:1 non-cooperative attachment under adaptive control.
(3) Cases of 1:1 attachment, carrying more momentum
In this case,the simulation was carried out for a small satellite attached to by a non-cooperative body with an inertia matrix of J1.Due to the increased momentum,the angular rate increased to the size as Eq. (33).
As shown in Fig.9,the new combination system under this condition tended to become stable after about 29 s.Compared with the control effect shown in Fig.5,the control time of the adaptive control is nearly half of gain scheduled PD control.Besides,compared with Fig.3,the variation of the control torque is much better, and only goes to saturation status for several seconds. We can see that the control effect of the system under the proposed adaptive control varies much less with the change of the momentum than the system under gain scheduled PD control. The system under the proposed adaptive control theme is more effective.
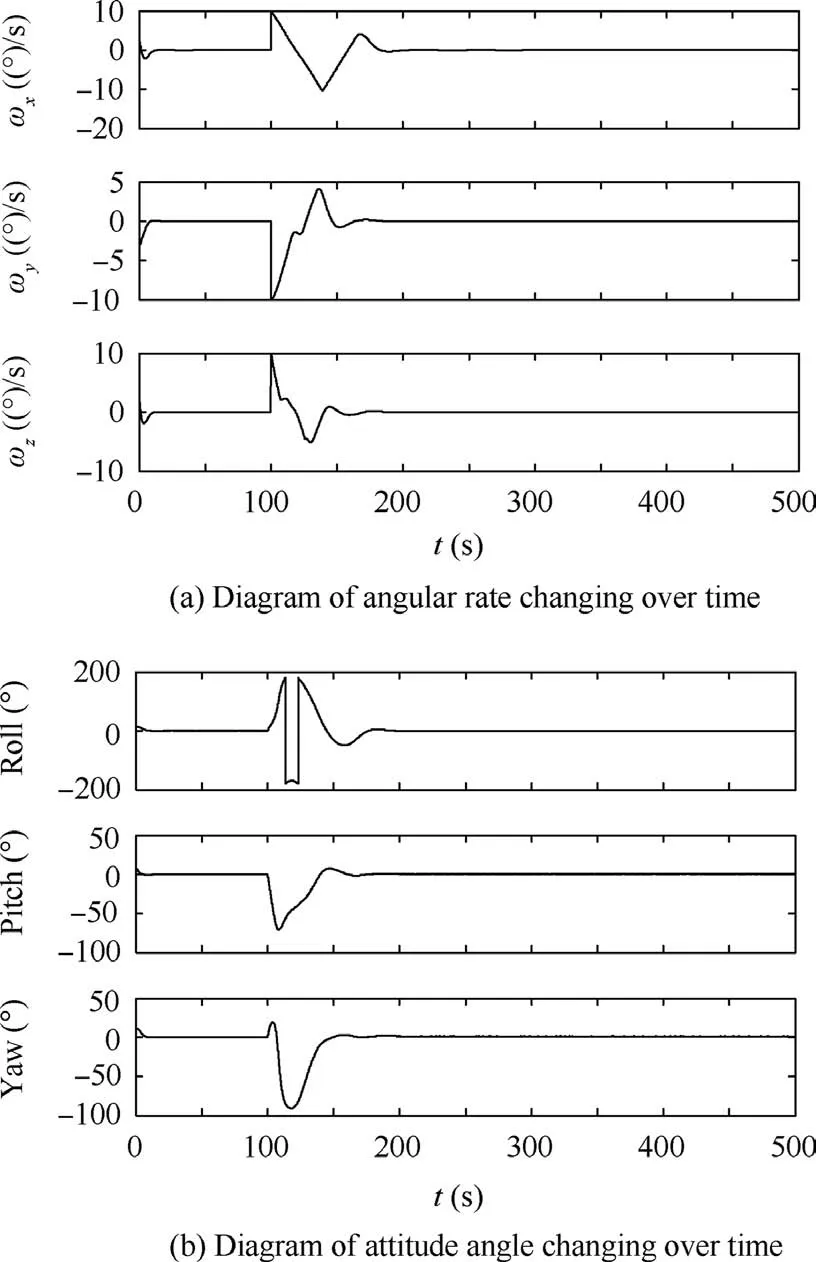
Fig. 8 Control effect of 1:10 non-cooperative attachment under adaptive control.
(4) Carrying dozens of times of momentum
The non-cooperative object may carry dozens of times the momentum of the original satellite system in order to cause deliberate destruction. A simulation was done based on the assumption that the satellite itself was still in good condition,but the great disturbance that the non-cooperative body brings needed to be resisted. The simulation was again done for a small satellite attached to by a non-cooperative body, having an inertia matrix of J1in this case.The control effect is shown in Fig. 10. Due to the increased momentum, the angular rate increased to dozens of times its original state:

The more momentum the non-cooperative body carried,the more obvious the change of the angular rate. As shown in Fig. 10, when the non-cooperative spacecraft maliciously attached to the small satellite, the system was able to recover a stable state under the adaptive control scheme.As previously mentioned, the simulation was done based on the assumption that the satellite itself was still in good condition,even after the momentum had changed dozens of times, as simulated above.The control effect of the system under the above situation can also compare with that in Fig.5.Therefore,the control system has strong robustness when it comes to different sizes of momentum being carried by the non-cooperative object.
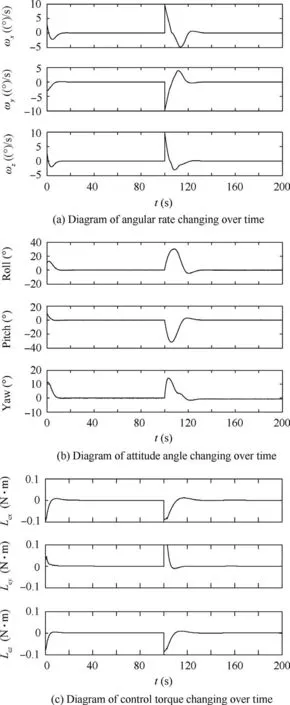
Fig. 9 Control effect of 1:1 non-cooperative attachment, carrying more momentum under adaptive control.
(5) Inertia estimation results
The inertia estimation results for the new combinations of 1:1 and 1:10 attachment are shown in Figs. 11 (a) and (b),respectively.In order to display these results clearly,only principal moments of inertia are included.
As shown in Fig. 11, Iestis the estimation results of inertia and I11,I22,I33are the main diagonal elements of Iest.Although the control law was designed based on estimating the inertia of the new combination, the actual estimation result was not quite ideal. For the 1:1 attachment case, the estimation result came close to the actual inertia of the new combination, but was not very accurate. For the 1:10 attachment case, the system barely estimated the actual inertia. The inertia difference was larger than estimated. However, the simulation curves show that,even if the control scheme did not provide an accurate estimation of inertia, the attitude control nonetheless achieved good results.
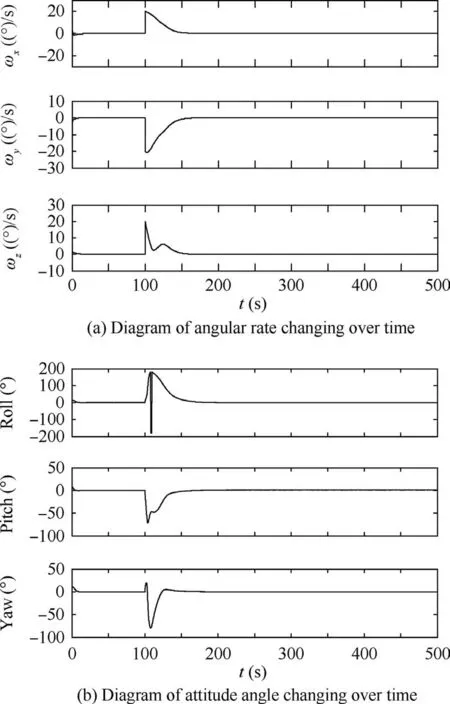
Fig. 10 Control effect of 1:1 non-cooperative attachment,carrying dozens of times of momentum under adaptive control.
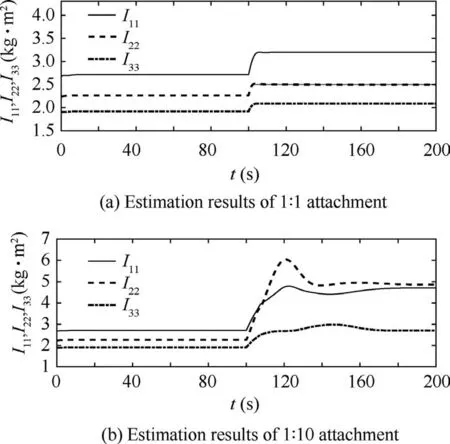
Fig. 11 Inertia estimation results of new combination.
5. Evaluation of simulation results
The simulation results and corresponding analysis of various unfavorable situations (i.e. unknown inertia parameters,carried momentum) verifies the robustness of the proposed adaptive control scheme. Although an accurate estimation of inertia was not fully achieved,and was only correct to a certain degree, the attitude control produced good results. Through the comparison between the proposed controller and other control systems in numerical simulations (including PD control theme and gain scheduled PD control theme), the advantages of controller can be shown. Ref. 14 used multinanosatellites to realize the 10-4accuracy level, but the momentum carried by non-cooperative spacecraft was not considered.The method proposed in this paper has better environmental adaptation. It can get over twenty of times of momentum and ten times of inertia attachment without the precise inertia estimation under the condition of single satellite control system,the results show the scheme has strong robustness. And we can prove that the new combined system under different situations can reach a stable state with precision and speed using the adaptive control scheme.
6. Conclusions
This paper studies the problem of non-cooperative body attachment, which can lead to the problem of system instability. Based on the kinematics and dynamics of the spacecraft,an adaptive control scheme based on inertia estimation has been proposed in this paper, and a detailed proof is given.The feasibility and effectiveness of the control scheme were verified by the simulation results and comparison with other control schemes. The proposed control scheme can be more sensitive to the state of the new combined system especially the change of the system inertia. Thus, the adaptive control scheme can not only effectively control the new combination system under all kinds of awful cases, but also work out the unknown inertia.In addition,it is easily to implement without extra cost,including the energy and the actuators.The control scheme cannot always achieve accurate estimation of inertia under any conditions,however.Research of the control theme for non-cooperative body attachment is highly relevant for orbit operation and space defense research.
Acknowledgement
This study was supported by the Fundamental Research Funds for the Central Universities, China (No. NS2014092).
 CHINESE JOURNAL OF AERONAUTICS2020年3期
CHINESE JOURNAL OF AERONAUTICS2020年3期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Experimental investigation on operating behaviors of loop heat pipe with thermoelectric cooler under acceleration conditions
- Investigation of hot jet on active control of oblique detonation waves
- Experimental study of rotor blades vibration and noise in multistage high pressure compressor and their relevance
- Unsteady wakes-secondary flow interactions in a high-lift low-pressure turbine cascade
- Effect of protrusion amount on gas ingestion of radial rim seal
- Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation
