Cooperative guidance strategy for multiple hypersonic gliding vehicles system

Jianglong YU,Xiwang DONG,Qingdong LI, Zhang REN, Jinhu LV

a School of Automation Science and Electrical Engineering, Science and Technology on Aircraft Control Laboratory,Beihang University, Beijing 100083, China

b Beijing Advanced Innovation Center for Big Data and Brain Computing, Beihang University, Beijing 100083, China

c Shananxi Key Laboratory of Integrated and Intelligent Navigation, Xi’an 710068, China

KEYWORDS Attack angle constraints;Attack time constraints;Cooperative guidance;Cooperative path planning;Entry guidance;Hypersonic vehicles

Abstract Cooperative guidance strategy for multiple hypersonic gliding vehicles system with flight constraints and cooperative constraints is investigated. This paper mainly cares about the coordination of the entry glide flight phase and driving-down phase. Different from the existing results,both the attack time and the attack angle constraints are considered simultaneously. Firstly, for the entry glide flight phase,a two-stage method is proposed to achieve the rapid cooperative trajectories planning,where the control signal corridors are designed based on the quasi-equilibrium gliding conditions. In the first stage, the bank angle curve is optimized to achieve the attack angle coordination.In the second stage,the angle of attack curve is optimized to achieve the attack time coordination. The optimized parameters can be obtained by the secant method. Secondly, for the driving-down phase, the cooperative terminal guidance law is designed where the terminal attack time and attack angle are considered. The guidance law is then transformed into the bank angle and angle of attack commands. The cooperative guidance strategy is summarized as an algorithm.Finally, a numerical simulation example with three hypersonic gliding vehicles is provided for revealing the effectiveness of the acquired strategy and algorithm.

1. Introduction

With the development of weapon technology, global rapid attack will become an important mode of combat in the future1,2where the weapons can strike targets anywhere on Earth in as little as an hour. A series of experiments, such as HTV-2 project and AHW project, have been carried out in the past few years.3These kinds of hypersonic glide vehicles can obtain a range more than thousands of miles (2400 miles for AHW and more than 6500 miles),3and have a large lateral maneuverability4through entering the atmosphere. Therefore,the hypersonic glide vehicle will become an important weapon owing to its high-speed,long-distance and large maneuverability,compared with the ordinary long-range missiles.However,with the development of radar technology and anti-missile technology,especially the cooperative interception technology,the ability of a single hypersonic vehicle will be greatly reduced. The development of multi-vehicle cooperative strike is more in line with future operational needs. The multimissile cooperative strike/guidance will greatly improve the operational efficiency from the aspects of cooperative decision-making,5cooperative penetration6and saturation attack.7The guidance of hypersonic glide vehicle is more difficult than that of axisymmetric vehicle because of its unique flight trajectory.8Therefore, it is important and interesting to study the cooperative guidance strategy of multiple hypersonic gliding vehicles system.

The flight process of a hypersonic gliding vehicle generally includes the powered phase, the adjustment phase, the entry gliding phase and the terminal guidance phase (driving-down phase). This paper mainly studies the cooperative guidance strategy of entry glide phase and terminal guidance phase,where the vehicles have the longest flight time and the greatest technology difficulty.One knows that the main purpose of the powered phase is making the vehicle have an appropriate initial entry state, which is not the research focus of this paper.This paper investigates the hypersonic gliding vehicle, which has strong maneuverability in the entry phase and terminal guidance phase. The terminal guidance phase can ensure the strike accuracy. The cooperative guidance of the entry glide flight phase can provide precise and advantageous initial conditions for initial terminal guidance phase. Then the cooperative guidance with impact angle and time constraints of the terminal guidance phase can further ensure effective attack.Therefore, it is necessary to solve the cooperative guidance problem by investigating the coordination strategy of the entry glide flight phase and driving-down phase. For the guidance issues of a single vehicle, there are mainly three kinds of guidance strategies in the entry glide phase. The first one is the reference-trajectory guidance method. This method has been successfully applied in the return of shuttle.9Researchers proposed a drag acceleration-energy profile design method to improve the reentry guidance accuracy.10Based on the reduced-order model, Ref.11generated three-dimensional trajectories by considering both longitudinal and lateral motions with energy as independent variables. Besides, Ref.12utilized the altitude-velocity profile to design an expected trajectory with no-fly zone and waypoint constraints. The second one is the predictor-corrector guidance method. It predicts terminal state online and gets control quantity by real-time correction,which has good robustness and real-time performance13,14and becomes the trend of reentry guidance. In order to deal with the complex multiple flight constraints, the Quasi-Equilibrium Gliding Condition (QEGC) was proposed in Ref.15, which can be used to rapidly design the bank angle curve satisfying the mission in the altitude-velocity plane.Based on the QEGC, Ref.16employed the numerical integration and fuzzy predictive logic technology to study the predictor-corrector entry guidance issues with no-fly zone and way-point constraints. In Ref.17,the altitude-velocity corridor was extended into a 3D corridor by using adding flightpath angle,and a novel corridor was constructed with a safety factor for the predictor-corrector guidance. The third method is online/offline optimization. In Ref.18, the trajectory optimization problems under complex multi-constraint were discretized into the non-linear optimal control problems and solved by Gauss pseudospectral method.In Ref.19,the analytical solution of gliding problem was studied, and real-time boundary corridors and online corrected control variables were given.In addition,the stochastic gradient particle swarm optimization method20,21and the pigeon inspired optimization method22were also effective for obtaining the optimal trajectories with multiple constraints. For the terminal guidance phase, the researchers were more concerned about the strike problems with terminal angle constraint,where the attack with large impact angle is effective to achieve the efficient strike.From a technical point of view,the techniques for attack with designed impact angle are mainly two kinds. One is the integrated guidance and control method with attack angle constraints, where the dynamic characteristic was considered.23,24The other is the optimal guidance scheme,which can have good convergence property and smooth trajectory.25,26

For the cooperative guidance strategy design of multiaxisymmetric missiles, researchers have investigated the cooperative guidance laws with the impact time coordination27,28and attack angle coordination.29,30The basic ideas are designing the cooperative guidance law with the terms composed of attack time or attack angle errors.The more complex problem is to consider the attack time constraint and the attack angle constraint simultaneously, which will lay the foundation for cooperative guidance with multiple constraints. The difficulty of this issue lies in how to design the form of guidance law and how to guarantee the stability of guidance system. There are two main solutions to these problems. One is to design a novel guidance law,in which both of the two cooperative constraints are taken into account.Ref.31designed a guidance law with attack angle constraint, and then added an item constructed by attack time error. Ref.32and Ref.33designed the form of guidance law with time-varying gains, and then obtained expressions of the gains by trajectory integral for satisfying the attack angle and attack time constraints.The other method is called a two-stage approach. The first stage is to realize the angle-constraint control, and the second stage is the time-constraint control. Based on this idea, Ref.34and Ref.35investigated the three-dimensional guidance issues with impact time and impact angle constraints. This two-stage method reduces the design difficulty and has much engineering significance.

In practical applications, the cooperative guidance with multiple constraints for multiple hypersonic gliding vehicles has very important significance in attack scenarios, especially against high-value ground targets or large ships.The cooperative attack with attack time and attack angle constraints can help to improve penetration capability and strike effect.Ref.36investigated the cooperative trajectory planning issues for two hypersonic gliding vehicles by optimizing the boundary curve of heading error angle with secant method. Ref.37designed the desired flight trajectory with undetermined parameters in the altitude-velocity plane. The relationship between expected flight time and undetermined parameters can be obtained by predictive correction method. Ref.38constructed the mapping between attack time and line-of-sight corner corridor boundary curve by using a neural network.Then the attack time can be controlled online by setting appropriate line-of-sight corner corridor boundary curve. Since the attack time can be controlled,37,38the cooperative guidance with attack time constraints can be achieved by choosing the same expected flight time of each vehicle, which is a classical two-level cooperative guidance architecture.39One sees that the achievements for the cooperative guidance strategy of multiple hypersonic gliding vehicles are rare, and the cooperative angle constraints and terminal guidance phase were not considered in the above results.36-38Moreover,for the cooperative terminal guidance issues in Refs.27-35, the velocity changing was not taken into account, which should be considered for the terminal guidance issues of hypersonic gliding vehicles.To the best of our knowledge, the cooperative guidance issues with both attack angle and attack time constraints for multiple hypersonic gliding vehicles are still open.

Motivated by the above current research status and future challenges,this paper studies the cooperative guidance strategy for multiple hypersonic gliding vehicles system of the entry gliding phase and the terminal guidance phase. Firstly, the flight constraints and cooperative constraints are modeled for the two phases. Then, for the entry gliding phase, a twostage method is employed to help plan the trajectories where the attack angle constraints are satisfied in the first stage and the attack time constraints are satisfied in the second stage.Thirdly, for the entry gliding phase, a cooperative terminal guidance law is designed where the terminal attack angle and the terminal attack time are considered simultaneously.Finally, an algorithm is presented to give the design steps of the cooperative guidance strategy for multiple hypersonic gliding vehicles system.

Compared with the former results, this paper possesses three aspects of contribution. Firstly, this paper investigates the rapid cooperative trajectory planning issues with attack angle and attack time constraints in the entry glide flight phase. One sees that the traditional trajectory planning methods in Refs.9-17cannot be directly employed for the cooperative trajectory planning issues because the attack angle and attack time constraints were not considered. Refs.36-38studied the cooperative trajectory planning issues in the entry glide flight phase; however, only the cooperative attack time constraint was dealt with while the cooperative attack angle constraint was ignored. Although the method in Refs.18-22can deal with the cooperative trajectory planning issues, the optimization time will be a large value, which is not suitable for online tasks. Secondly, a novel two-stage method is proposed to deal with the cooperative constraints of the cooperative trajectory planning issues. Refs.34,35investigated the three-dimensional guidance issues with impact time and impact angle constraints by using the two-stage method.However, the research objectives were axisymmetric missiles,and the methods34,35cannot be directly utilized in the cooperative trajectory planning for multiple hypersonic gliding vehicles system. Thirdly, the attack angle and the attack time constraints are considered simultaneously in the cooperative terminal guidance law, where velocity dynamic loop is considered. Although the cooperative terminal guidance issues with attack angle and the attack time constraints were processed,27-35the velocity was assumed to be constant. The estimation of time-to-go is modified in this paper by designing an additional gain to compensate the effects of velocity changing. Ref.12investigated the terminal guidance for hypersonic gliding vehicle with terminal attack angle constraint;however, the attack time constraint was not considered.Moreover, the terminal guidance phase was not considered in Refs.36-38.

The remaining parts of this paper are arranged as follows.The cooperative guidance problem formulation is given in Section 2,where the flight constraints and the cooperative constraints are modeled.Section 3 gives the main results,including the cooperative guidance strategy design for entry glide flight phase and driving-down phase. Numerical simulation results for the proposed strategy are given in Section 4. Section 5 summarizes this paper.

2. Cooperative guidance problem formulation

In this section, the problem description and the investigation objective are presented.

2.1. Dynamic model of hypersonic gliding vehicles

Consider a multiple hypersonic gliding vehicles system with N vehicles. Using a rotating spherical Earth model, the pointmass dynamics of hypersonic gliding vehicle can be modeled by Ref.18as

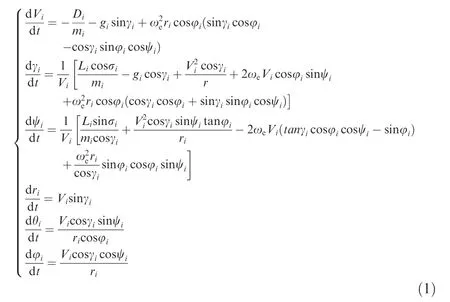
where i=1,2,···,N. Define the altitude as hi=ri-R0.

The expressions of Diand Liare given as

where ρiis defined as ρi=ρ0exp（-hi/hs）. ρ0is the density of sea level and hsis a standard reference altitude.

2.2. Flight constraints

(1) Entry trajectory constraints The typical entry trajectory constraints are usually designed as

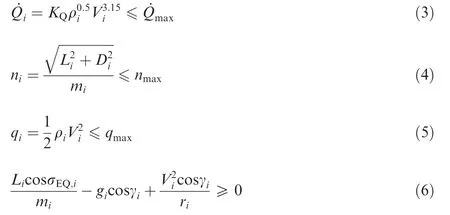
where KQis the heat transfer coefficient, and ˙Qmax, nmaxand qmaxare the maximum limits of ˙Qi, niand qirespectively.Inequality(6)is called the Quasi-Equilibrium Glide Condition(QEGC),15,16where σEQ,iis the bank angle under QEGC.Note that constraints(3)-(5)are rigid constraints which must be satisfied, and Inequality is a soft constraint.

(2) Control constraints

Note that the angle of attack αiand bank angle σiare the control inputs for entry vehicles. In order to satisfy the above trajectory constraints and the range constraint, the control inputs should be constrained within a reasonable extent,that is

where αmin,αmax,σmaxare the minimum and maximum bounds.Note that the values of αmin,αmax,σmaxmay be changed in the different flight conditions, which will be discussed in the later sections.

2.3. Cooperative guidance problem

From the flight process of the hypersonic gliding vehicle, the entry process usually contains two phases. The first stage is called entry glide flight phase,which is usually the longest trajectory of a vehicle.10The second stage is called the drivingdown phase or terminal guidance phase, where the terminal states are usually constrained to be certain values to achieve better attacking effect.

The cooperative guidance strategy for multiple hypersonic gliding vehicles system can be illustrated as the following picture with two vehicles for instance:

In Fig.1,A0and B0are the initial positions,A1and B1are the terminal positions of the first stage of entry glide flight phase,A2and B2are the terminal positions of the second stage of entry glide flight phase,T is the position of the visual or real target, ψAand ψBare the desired attack angles.

(1) Entry glide flight phase

In this phase (A0→A1→A2or B0→B1→B2), the cooperative guidance strategy is designed to require the multiple hypersonic gliding vehicles arriving at the expected object point with cooperative time constraint and cooperative heading angle constraint while satisfying the satisfying constraints(3)-(7). This paper considers the trajectory rapid planning issues. Since the constrained entry trajectory rapid planning issues with multiple constraints, especially cooperative constraints, are much complicated, this paper proposes a twostage method.

(A) First stage

In the first stage(A0→A1or B0→B1),the angle of attack αiis pre-designed according to a nominal angle-of-attack profile, and the bank angle profile of σiis determined by certain algorithms. The design objective is to generate a trajectory with cooperative heading angle constraint while satisfying constraints (3)-(7). The initial and terminal state constraints are given as

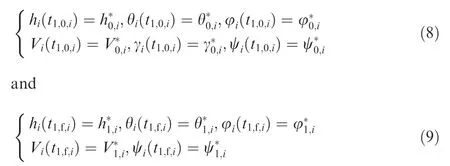
where t1,0,iis the initial time at the beginning of the entry phase, t1,f,iis the terminal time of the first stage, and the state variables with subscript ‘‘0,i”,‘‘1,i” and superscript ‘‘*” mean the initial and the terminal values of the state variables of the first stage of entry glide flight phase respectively.

(B) Second stage

In the second stage (A1→A2or B1→B2), the bank angle σiis designed to be a fixed value(zero),and the angle of attack profile of αiis designed by certain algorithms. The design objective is to generate a trajectory with cooperative flight time constraint while satisfying constraints (3)-(7). The initial and terminal state constraints are given as

Fig. 1 Cooperative guidance strategy for multiple hypersonic gliding vehicles.

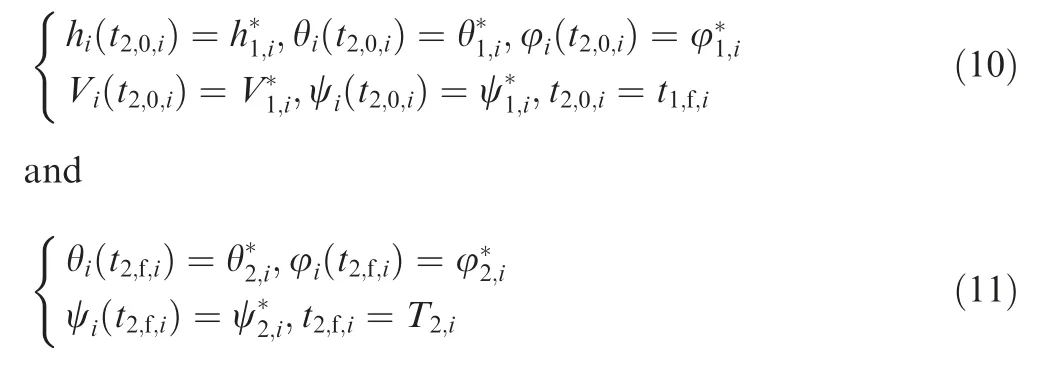
where t2,0,iis the initial time of second stage, t2,f,iand T2,iare the real terminal time value and the desired terminal time value of the second stage respectively, and the state variables with subscript ‘‘1,t”,‘‘2,i” and superscript ‘‘*” mean the initial and the terminal values of the state variables of the second stage of entry glide flight phase respectively.

Remark 1. In this phase (A0→A1→A2or B0→B1→B2),the cooperative guidance strategy can also be called the cooperative trajectory planning strategy. In practical applications, the cooperative guidance with multiple constraints for multiple hypersonic gliding vehicles has very important significance in attack scenarios,especially against high-value ground targets or large ships.The cooperative attack with impact time constraint can improve the pressure of antimissile system.Besides,the cooperative attack with impact angle constraint for hypersonic gliding vehicle can improve strike efficiency and penetration, which has been widely employed in conventional missiles. However, less researches have been done on the trajectory planning issues with attack angle constraint for hypersonic gliding vehicle, and thus, the cooperative attack with angle constraint may be a research point in the future.The results in Refs.36-38only considered the cooperative attack time constraint, and the cooperative attack angle constraint cannot be addressed. The methods15-17may be unable to solve the cooperative trajectory planning. In addition, this paper mainly cares about the trajectory planning issues to obtain the ideal control signals, and one can utilize the Linear Quadratic Regulator (LQR) method to achieve the control signal tracking.

(2) Driving-down phase

This phase (A2→T or B2→T) is also called the terminal guidance phase.In this phase,the attack angles(the flight path angle and heading angle) are required to be certain values to improve the attacking effect for single vehicle. However, for multiple hypersonic gliding vehicles, the cooperative arrival time constraint is also required, that is, time-to-go is required to achieve the coordination. The angle of attack and the bank angle are to be designed simultaneously for achieving the above objective. The initial and terminal state constraints are given as

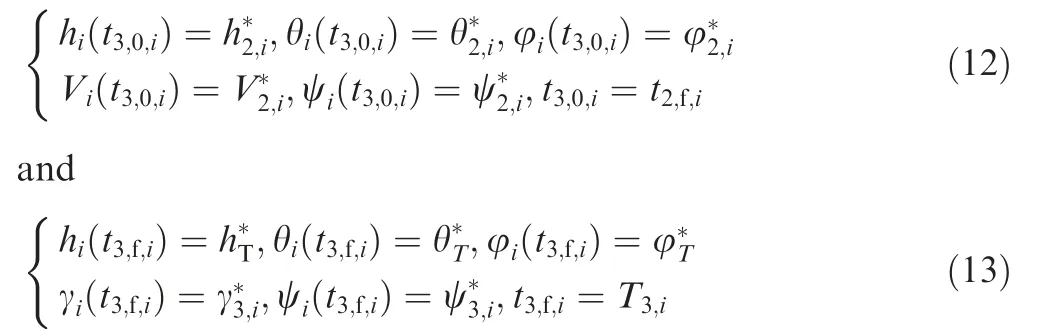
where t3,0,iis the initial time of the driving-down phase, t3,f,iand T3,iare the real terminal time value and the desired terminal time value of the driving-down phase respectively,（θ*T,φ*T,h*T） is the three-dimensional coordinates of the target,and state variables with subscript ‘‘2,i”,‘‘3,i” and superscript‘‘*” mean the initial and the terminal values of the drivingdown phase respectively.Remark 2. In this phase(A2→T or B2→T),the cooperative terminal guidance law is required to be designed. Note that Refs.36-38did not consider the terminal guidance issues.Moreover, the methods27-35cannot be directly utilized in the cooperative trajectory planning for multiple hypersonic gliding vehicles for special dynamics.

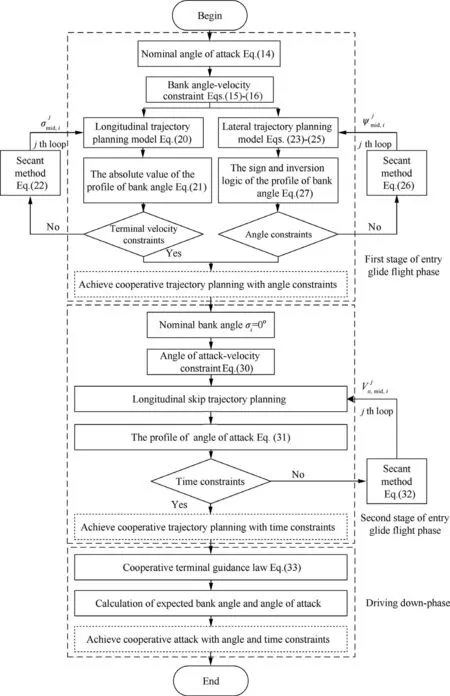
Fig. 2 Flowchart for designing cooperative guidance strategy.

Fig. 3 Interaction topology of three vehicles.

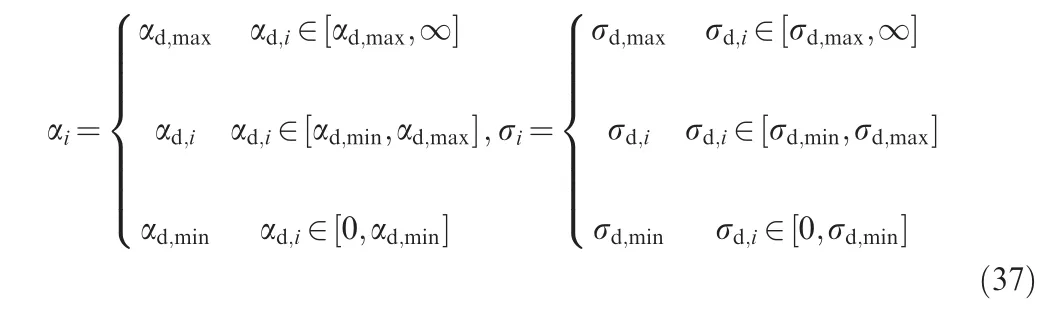
where αd,max, αd,min, σd,maxand σd,minare positive constants.

Remark 7. From Eq. (35), one sees that the interaction topology of the multiple hypersonic gliding vehicles system should have certain limitations,which means that each vehicle should get at least one neighbor’s information.The parameters κi, αd,max, αd,min, σd,maxand σd,minin the guidance laws and should be chosen according to the actual demand of the flight conditions. In the driving-down phase, the control constraints are mainly concerned by using the saturation manipulation Eq.(37). The trajectory constraints are not considered here because this problem is a complicated one and there are rare achievements. This paper only gives a simple method in this phase and the details will be investigated in future work.

To summarize the conclusions of the above subsections, a flowchart is given as Fig. 2 to describe the procedures for designing the cooperative guidance strategy for multiple hypersonic gliding vehicles system.

4. Numerical simulations

In this section, a numerical simulation experiment is performed on a computer (Intel Core i7, 3.2 GHz) to show the effectiveness of the proposed strategy. In this paper, the CAV-H model12is chosen as the simulation objective to investigate the cooperative guidance strategy for three hypersonic gliding vehicles,which means N=3.The interaction topology is described as in Fig. 3, which is connected and mainly cared about in the driving-down phase. According to the theoretical results,the effectiveness of the proposed algorithm is not much affected by the quantity of the vehicles.If the initial conditions and planning tasks for multiple hypersonic gliding vehicles system are reasonable and appropriate, the cooperative guidance operation can always be achieved.Moreover,if the number of vehicles is large, the cooperative group guidance strategy can be adopted, where multiple vehicles are divided into groups.Thus, the number of vehicles in each group does not need to be very large. The constraints in Eqs. (3)-(5) are given as ρ0=1.225 kg/m3,hs= 7110 m, ˙Qmax=6000 kW/m2,qmax=40 kPa, nmax=4g0, where g0=9.8 m/s2.

4.1. Simulation results of entry glide flight phase

(1) First stage

The initial and the terminal states of the three vehicles are shown in Tables 1 and 2.The symbol‘*’means that the corresponding state is not constrained.

For the nominal angle of attack profile(24),the parameters are chosen as α1,max=40°, α1,min=10°, V1,max=5000 m/s and V1,min=2000 m/s. For the lateral trajectory planning algorithm (22), one can obtain σmid,1=29.85°, σmid,2=26.27°and σmid,3=27.99°. Choose Vψ,1=4000 m/s, Vψ,2=3000 m/s,Δψ1=0.9°, Δψ2=0.3°, VC,1=5520 m/s, VC,2=5940 m/s.For the lateral trajectory planning algorithm Eq. (26), one can obtain ψmid,1=20.72°, ψmid,2=17.42°and ψmid,3=18.29°. Besides, one can get the terminal flight time as t1,f,1=1245.8 s, t1,f,2=1268.2 s and t1,f,3=1257.8 s in the simulation results.

In this phase, the terminal errors are shown as follows:

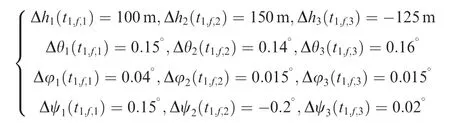
The simulation results of this stage are shown as follows.The ground trajectories in the first stage of the entry glide flight phase are displayed in Fig.4.The trajectory constraints in the altitude-velocity plane are plotted in Fig. 5, which shows thatthe rigid constraints (3)-(5) are satisfied. The control signals are shown in Fig. 6. Fig. 7 displays the curves of the heading angles, which indicates that the attack angle constraint is satisfied.

Table 1 Initial states in the first stage of entry glide flight phase.

Table 2 Terminal states in the first stage of entry glide flight phase.

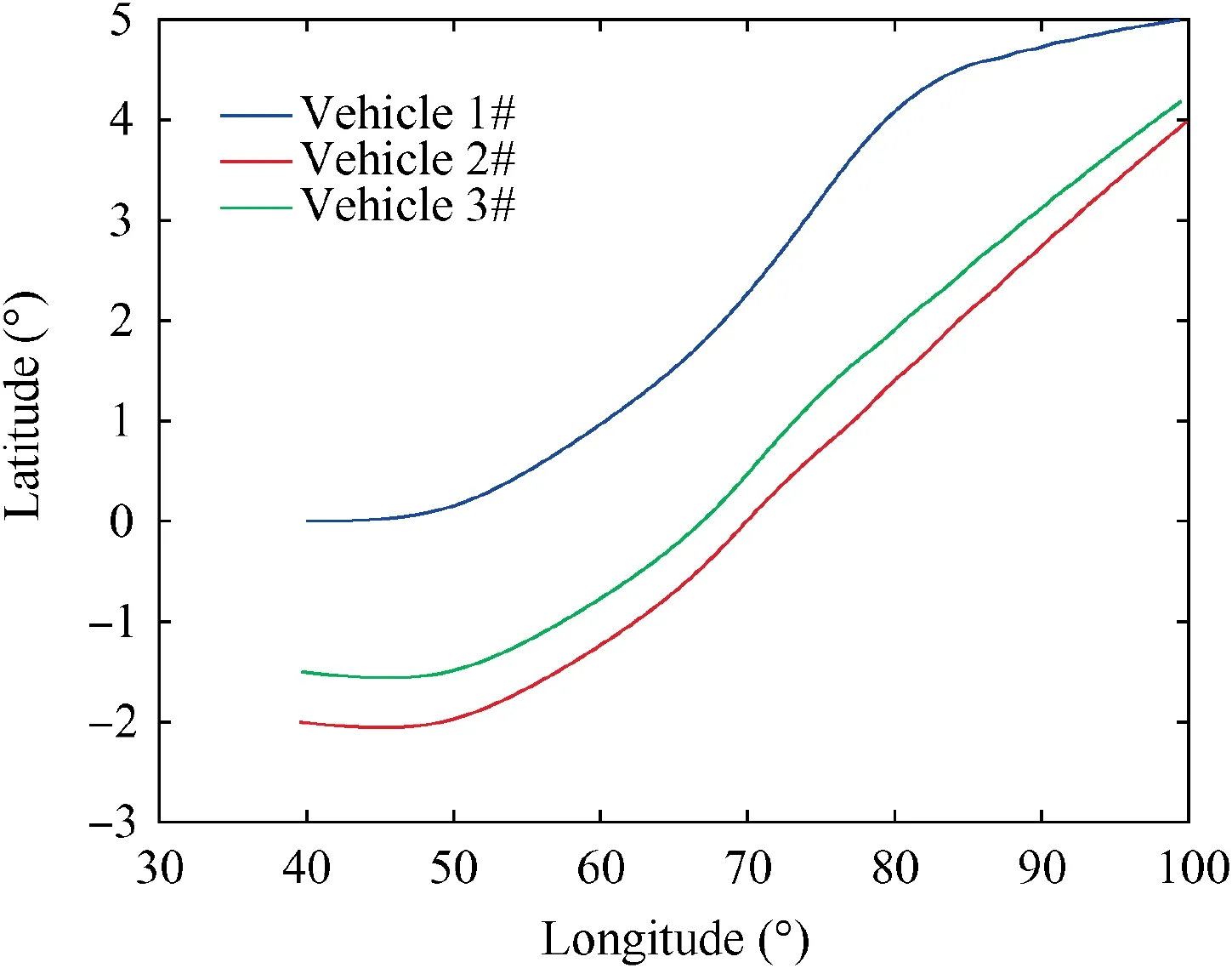
Fig. 4 Ground trajectories in the first stage of entry glide flight phase.

Fig. 5 Trajectory constraints in altitude-velocity plane.

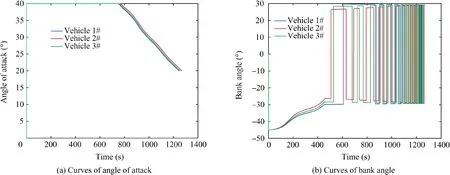
Fig. 6 Curves of bank angles and angles of attack.

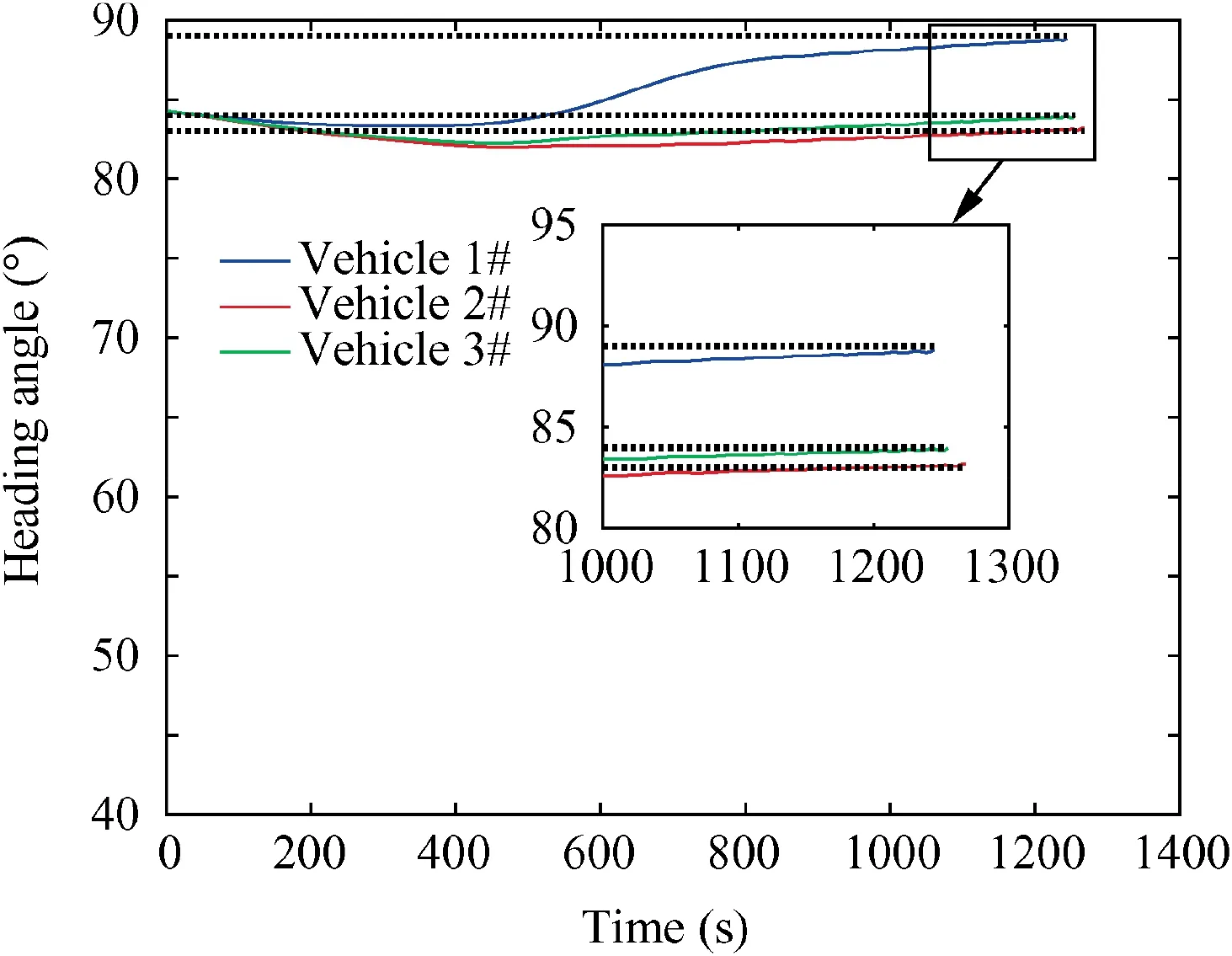
Fig. 7 Curves of heading angles.

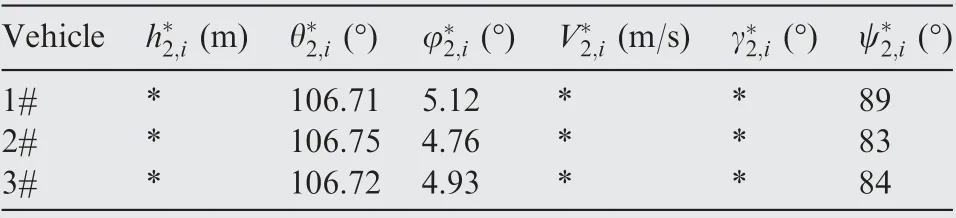
Table 3 Terminal states in the second stage of entry glide flight phase.

(2) Second stage

The terminal states of the three vehicles in this stage are shown in Table 3. The visual target is set as（109.9112°,5.1555°,0m）, which means that the terminal states of the three vehicles in the first stage are flying aiming at the visual target.

Choose αEQ,min,i（Vi）=14°, αEQ,max,i（Vi）=20°, VT,1=3000 m/s, αmid,i=16°. The desired cooperative terminal time is chosen as T2,i=1576s. The optimized solution is calculated as Vα,mid,1=2623 m/s, Vα,mid,2=2386 m/s and Vα,mid,3=2814 m/s.

The simulation results of this stage are shown as follows.The relationship of angle of attackαiand the flight range or flight time t2,f,i=fq,f,i（αi）is shown in Fig.8,where one sees that the relationship is approximately a quadratic function. The designed angle of attack corridor is displayed in Fig. 9. The ground trajectories in the second stage of the entry glide flight phase are shown in Fig. 10. The curves of the velocities and altitudes are plotted in Fig.11,where the three vehicles achieve the attack time coordination through different jump maneuvers. Besides, the curves of the angle of attack are depicted in Fig.12.Therefore, the cooperative trajectory planning with attack angle and attack time constraints of entry glide flight phase is achieved.

Fig. 8 Relationship of angle of attack and flight range or flight time.

Fig. 9 Angles of attack corridor curves.

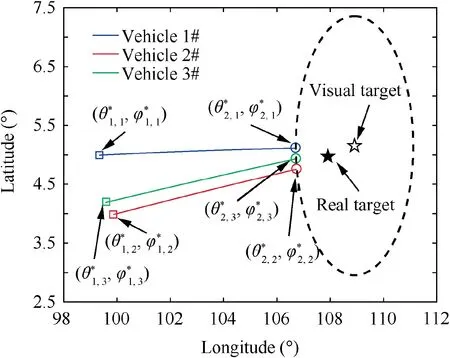
Fig. 10 Ground trajectories in the second stage of entry glide flight phase.

The trajectory constraints (3)-(6) and control constraints(7) of the entry glide flight phase are illustrated in Figs. 13 and 14. One sees that the constraints (3)-(7) can be satisfied by using the proposed method while the cooperative guidance tasks are achieved.

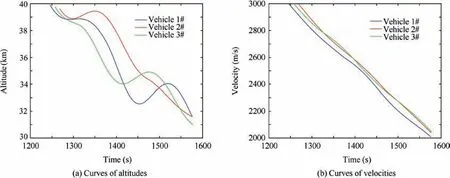
Fig. 11 Curves of velocities and altitudes.

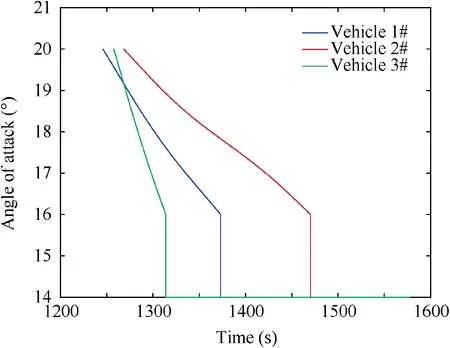
Fig. 12 Curves of angles of attack.

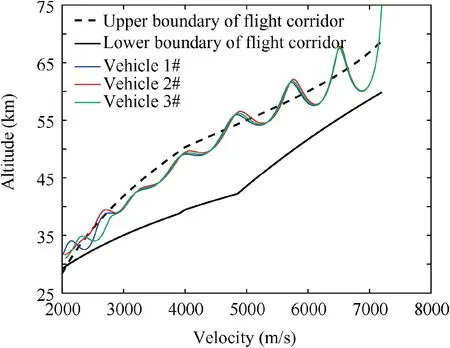
Fig. 13 Trajectory constraints in altitude-velocity plane.

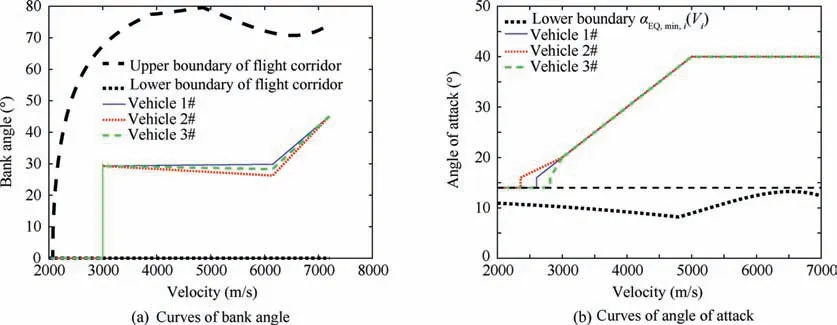
Fig. 14 Control signals and their constraints.

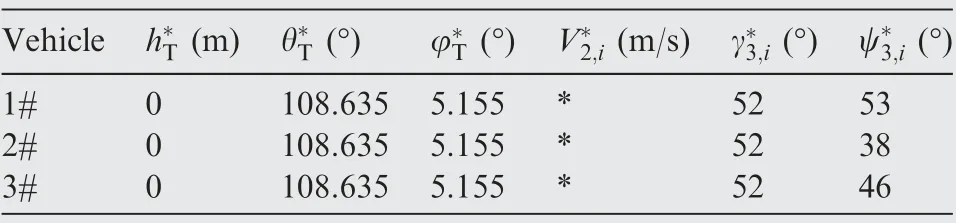
Table 4 Terminal states of driving-down phase.

Fig. 15 Three-dimensional trajectories of driving-down phase.

Note that Refs.36-38only cared about the impact time coordination of the entry glide flight phase; however, the impact angle coordination and the terminal guidance phase were not considered in Refs.36-38. The proposed cooperative guidance strategy of this paper can consider the impact time and impact angle coordination simultaneously in both entry glide flight phase and terminal guidance phase,which has more and better performance. Besides, twice secant methods with single variable are used in this paper,and once secant method with single variable and multiple variables are used in Ref.36and Ref.37,respectively. Besides, abundant online training is required in Ref.38and the time cost is high.Since the secant method is easy to realize, the proposed strategy of this paper has good simplicity performance.From the simulation results,the operating time for the methods in this paper is 0.98 s. Besides, the operating time for methods in Ref.36and Ref.37is 1.25 s and 5.4 s,respectively. Thus, methods of this paper have satisfying realtime performance.

4.2. Simulation results of driving-down phase

Fig. 16 Curves of velocities.

Table 4 lists the desired terminal states of the driving-down phase.The parameters in the terminal guidance law are chosen as κi=22, αd,max=20°, αd,min=0°, σd,max=25°and σd,min=0°. In this phase, the target is assumed to move to a new position in Table 4.

Three-dimensional trajectories are shown in Fig.15.Fig.16 displays the curves of the velocities. Fig. 17 depicts the curves of the angle of attack and bank angle,which are bounded.The terminal attack angle and attack time are shown in Fig.18 and Fig. 19. One sees that the cooperative attack time error is within 1 s.The line-of-sight angle errors of three vehicles in lateral plane and longitudinal plane are 0.1°,0.15°,0.12°and 0.2°,0.25°, 0.18°, respectively. The attack angle error and attack time error are small ones. Therefore, the cooperative terminal guidance with attack angle and attack time constraints is achieved.

4.3. Monte-Carlo simulation results

In this part, the Monte-Carlo simulation results with 50 flight trajectories are given to test the robustness of the proposed method.The uncertainties of the initial flight condition perturbation and aerodynamic parameters perturbation are specified as in Ref.37. The simulation results are presented as follows.

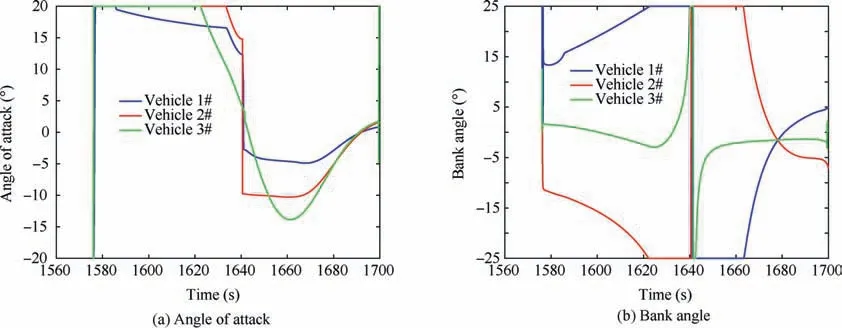
Fig. 17 Curves of angle of attack and bank angle.

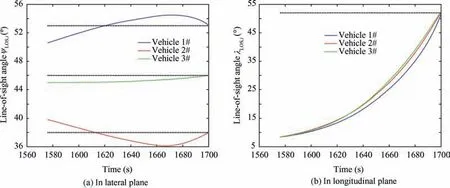
Fig. 18 Curves of line-of-sight angles.

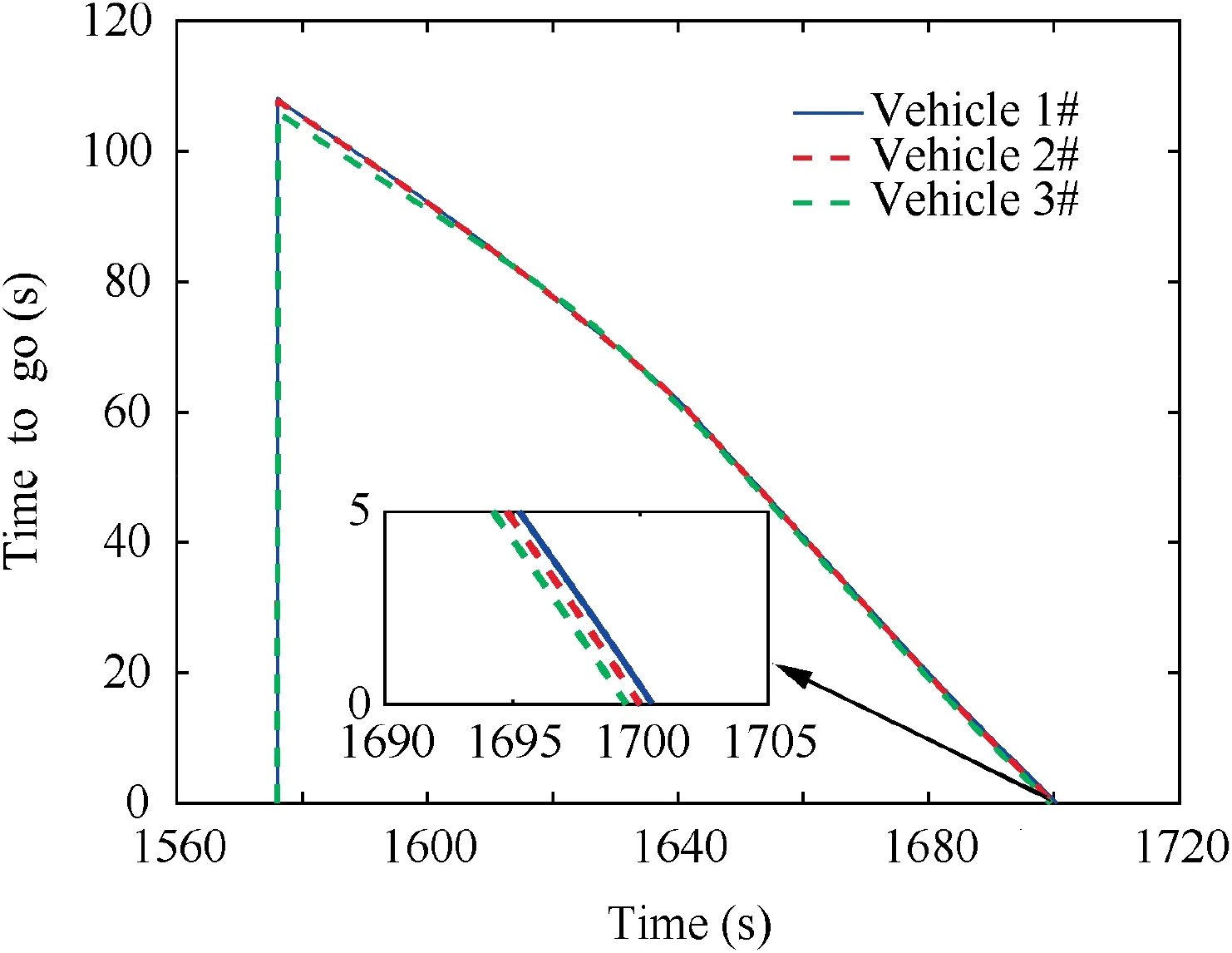
Fig. 19 Curves of time-to-go.

Figs. 20 and 21 show the ground trajectories under uncertainties of the entry glide flight phase and the driving-down phase. The standard deviations of terminal states of the three stages are presented in Tables. 5-7.denotes the standard deviation of the difference between state X and its desired value of the nth phase as in Section 2.3. s-T,n,idenotes the standard deviation of the difference among three vehicles of the nth phase.From the simulation results,the attack time and attack angle errors are within small bounds, which indicates that the cooperative guidance with attack angle and attack time constraints is achieved. Therefore, the robustness and the feasibility of the proposed cooperative guidance strategy of multiple hypersonic gliding vehicles system subject to uncertainties can be guaranteed.

5. Conclusions

This paper studied the cooperative guidance issues for multiple hypersonic gliding vehicles system. Both the attack time and the attack angle constraints were taken into account. As for the entry glide flight phase, a two-stage method was proposed to achieve the rapid cooperative trajectories planning.The first stage was aimed at achieving the attack angle coordination by optimizing the bank angle,and the second stage was to achieve the attack time coordination by optimizing the angle of attack.For the driving-down phase,the cooperative terminal guidance laws were designed based on the optimal terminal guidance law where the attack time was also considered. An algorithm was provided to summarize the cooperative guidance strategy. It is of interest and significance to further study potential waypoint constraint-based cooperative trajectories planning strategy and the trajectory constraints of driving-down phase in detail. Besides, the design criterion of the demarcation points for the two stages will be the future work.

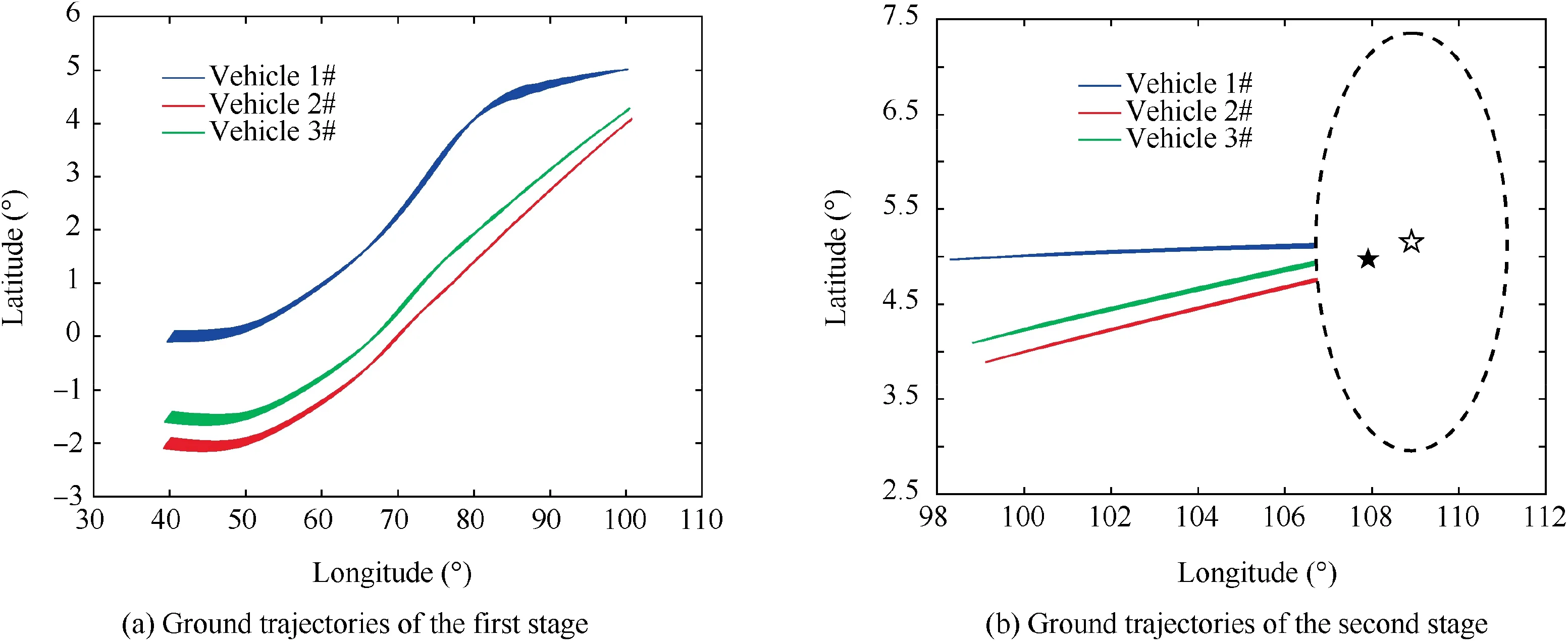
Fig. 20 Ground trajectories under uncertainties of entry glide flight phase.

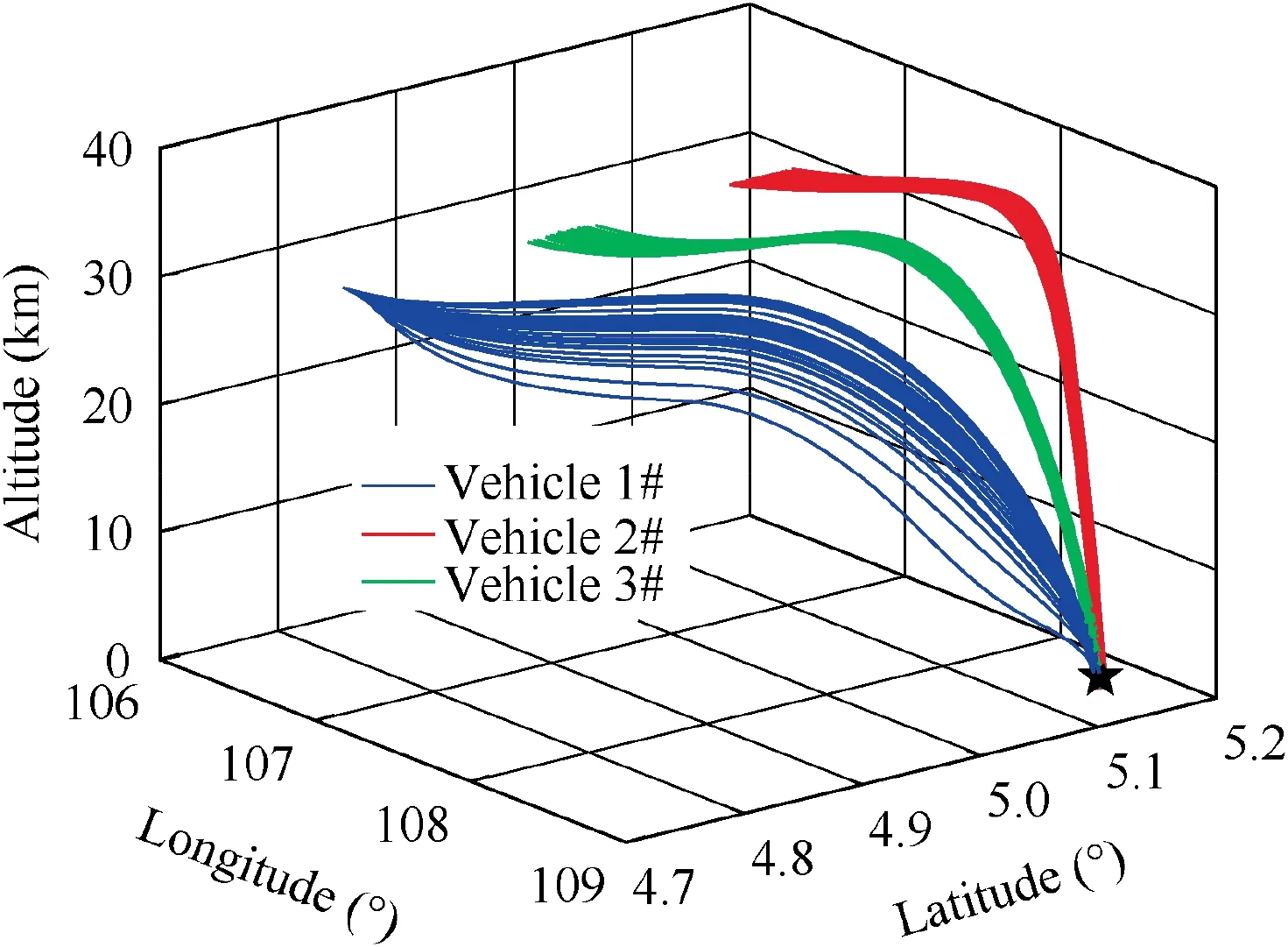
Fig. 21 Trajectories under uncertainties of driving-down phase.

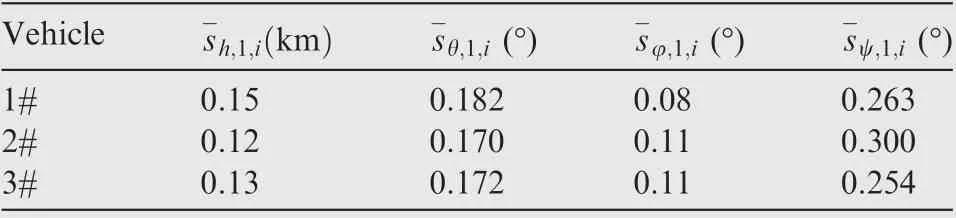
Table 5 Standard deviations of terminal states in the first stage.

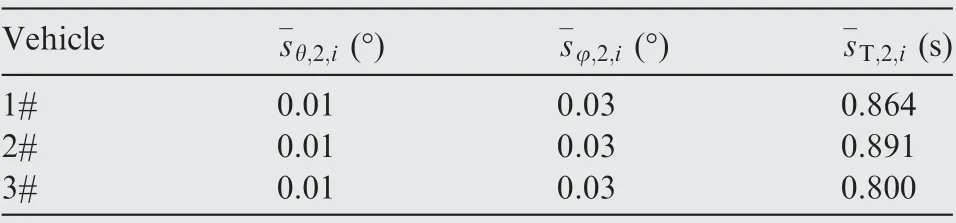
Table 6 Standard deviations of terminal states in the second stage.

Table 7 Standard deviations of terminal states of drivingdown phase.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos.61922008, 61973013, 61873011,61803014), the Innovation Zone Project of China(No.18-163-00-TS-001-001-34), the Beijing Natural Science Foundation of China(No.4182035),the Young Elite Scientists Sponsorship Program by CAST of China(No.017QNRC001),the Aeronautical Science Foundation of China(No.20170151001), the Special Research Project of Chinese Civil Aircraft,the State Key Laboratory of Intelligent Control and Decision of Complex Systems,the Key Laboratory of System Control and Information Processing, and the Shananxi Key Laboratory of Integrated and Intelligent Navigation(No.SKLIIN-20180105).