Optimal guidance against active defense ballistic missiles via differential game strategies

Hizho LIANG, Jinying WANG,*, Yonghi WANG, Linlin WANG,Peng LIU

a School of Aeronautics and Astronautics, Sun Yat-sen University, Guangzhou 510275, China

b Beijing Institute of Space Long March Vehicle, Beijing 100076, China

KEYWORDS Active defense;Ballistic missile;Differential game;Guidance law;Optimal guidance

Abstract The optimal guidance problem for an interceptor against a ballistic missile with active defense is investigated in this paper. A class of optimal guidance schemes are proposed based on linear quadratic differential game method and numerical solution of Riccati differential equation.By choosing proper parameters, the proposed guidance schemes are able to drive the interceptor to the target and away from the defender simultaneously.Additionally,fuel cost,control saturation,chattering phenomenon and parameters selection were taken into account. Satisfaction of the proposed guidance schemes of the saddle point condition is proven theoretically. Finally, nonlinear numerical examples are included to demonstrate the effectiveness and performance of the developed guidance approaches. Comparison of control performance between different guidance schemes are presented and analysis.

1. Introduction

In order to cope with both civil and military threats to today’s space, air, navy and land facilities brought by missiles, interception becomes a significant research topic and are widely investigated in recent decades. The appearance of modern interceptors such as Kinetic Kill Vehicle(KKV)and Exoatmospheric Kill Vehicle(EKV)provide adequate protection for the facilities against missiles,especially against the Ballistic Missile(BM) which possesses hypersonic speed, strong damage, and usually plays a vital part in an attack mission. However, as the development of missile penetration techniques, ballistic missiles were equipped with high performance sensors and power plants. That makes the ballistic missiles become more sophisticated and maneuverable than traditional unpowered ones. Moreover, active defense techniques are employed by ballistic missiles as an effective countermeasure,and the ballistic missiles could fly with an active defender during the midcourse phase. As a result, interceptors against active defense ballistic missiles in an attack-defense engagement is required to attack the missile and evade the defender simultaneously.And we focus on the guidance approaches of the interceptor in this paper.

In traditional pursuit-evasion scenarios, there are two agents, a pursuer and an evader, where the pursuer tries to reach a relatively small distance with respect to the evader.1A number of classical guidance laws such as Pure Pursuit(PP), Proportional Navigation (PN), augmented proportional navigation (APN) approaches were proposed for the pursuer.In addition, some guidance schemes using finite-time control strategy,multi-objective optimization,fractional calculus algorithm,and sliding mode control approach were investigated in some certain cases, e.g. asteroid hovering and landing, space maneuvering, hypersonic vehicle flying.2-6Nevertheless,multi-agent pursuit-evasion is also interesting and important which has been studied in recent years.Based on dynamic Voronoi diagrams, decentralized schemes were developed to solve a multi-agent problem where a number of pursuers were assigned to capture an evader.7In Ref.8, a group of pursuers intercepting several evaders was investigated with the assumption that the aims of the evaders were known. In order to improve the performance of target tracking, approaches for multi-pursuers by controlling the engagement geometry near interception were proposed and validated by a three-agents interception engagement.9

In most interesting cases, the guidance problem involves adversaries as pursuers and evaders, and thus the utilization of differential game strategy is both natural and appealing.Actually, guidance problem of pursuit and evasion motivated the development of differential game theory by Isaacs.1Considering the air-to-air missile guidance problem of one pursuer and one evader,schemes based on norm differential game and linear quadratic differential game were proposed with linearized kinematics,10and only one pursuer and one evader are considered in engagement. Both the ideal dynamics model and first-order dynamics model were investigated, and comparisons between differential game approach and optimal control approach were given. In Ref.11, guidance problem of satellites interception was solved by differential game strategies. Based on linearized kinematics, a multi-agent scenario with several pursuers capturing one evader is investigated in Ref.12, and guidance laws using linear quadratic differential game were developed,which is proven to be superior than traditional guidance strategies.

Because of the development of active defense technique,there is not only pursuers and evaders but also defenders in attack-defense scenarios. Therefore, guidance law of threeadversary engagement has received considerable attention in recent years.13-21One of the initial researches of this problem was Ref.13, where Boyell derived the closed-form relations under the assumption of constant-bearing collision course,and Shneydor in Ref.14presented a few derivations in compact form which simplified one condition of Ref.13.Similar to Lineof-Sight(LOS)guidance law,guidance approaches were developed for defenders in Ref.15by using the fact that,the defender was able to intercept the attack missile if it remained on the line joining the attack missile and target. A game formulated as three-agent problem with a missile,a target,and a defender was solved by numerical solution of Riccati equation.16Impulse function was employed to represent disappearance of the defenders after interception. In order to intercept the attack missile,cooperative guidance laws using norm differential game strategy were proposed in Ref.17for both the target and defender with arbitrary-order linear dynamics. However,the guidance law of the attack missile was not investigated in Ref.17and assumed to be linear and known in the analysis and simulation. A cooperative guidance scheme using norm differential game was developed in Ref.18by solving a twopoint boundary-value problem. Based on linear quadratic differential game strategies,a three-agent engagement were investigated in Ref.19, and three scenarios of defender and target with linearized kinematics were considered.But the attack missile, whose guidance law was assumed to be known, was assigned heading to the target without avoiding the defender in the engagement in Ref.19. By considering the limitations of linearized kinematics, nonlinear guidance problems were solved in Ref.20by using sliding mode control strategies,where a novel variable representing zero-effort velocity was proposed.

The cooperation of target and defender is an interesting topic to research. On the other hand, the guidance problem of the attack missile or the interceptor in a three-adversary engagement scenario is also useful but rarely investigated.22-26In Ref.22, optimal guidance laws based on arbitrary-order linear dynamics were proposed for a missile to pursue a target while evading defender. But the derivation was computational complex and only the effectiveness of the cooperation strategy of target and defender was validated.Guidance approaches for attack missiles were derived in Refs.23,24where dynamic models in analysis were assigned to be ideal, and the approaches were not adequate for situations with large initial errors. In Refs.25,26, guidance strategies based on differential game were developed based on ideal dynamic models without considering fuel cost and chattering in control signals, ignoring which can jeopardize the mission in practical situations.

It is worthy to point out that the guidance laws of the attack missiles were assumed to be known or linear or both in most of the aforementioned literature such as Refs.16-20,and the attack missiles in validations were assigned heading to the target straightly without notifying the defender.Although Refs.22-26investigated the guidance problem for attack missile, the models considered in analysis were ideal while the schemes ignored fuel cost,chattering and control saturation. In addition to these issues, there are few studies on ballistic missile interception have been done, adversaries of which possess more limited maneuverability, larger relative velocity,and less decision time than that of air-to-air scenario.Inspired by these facts,it is desirable to develop optimal guidance schemes with intuitive formulations for interceptors against active-defense ballistic missiles. The schemes are able to drive the interceptor to the ballistic missile while evading the defender under limited maneuverability and fuel cost. To the best of the Authors’ knowledge, such type of guidance problem has not been investigated in the existing literature.

2.4. Linearized kinematics

As can be seen in Fig.1,there are two collision triangles in the engagement scenario. One is between the interceptor and the maneuvering target, and the other is between the interceptor and the defender.During the endgame,relative speed between the players is very high, more than Mach 15 commonly, while the acceleration generated by thrusters thereon is usually less than 100 m/s2. Therefore, it is reasonable to assume that the players’ speed is constant and the dynamics of each player in game can be represented by first-order strictly proper dynamics as follows with time constant εifor i = I,M,D:

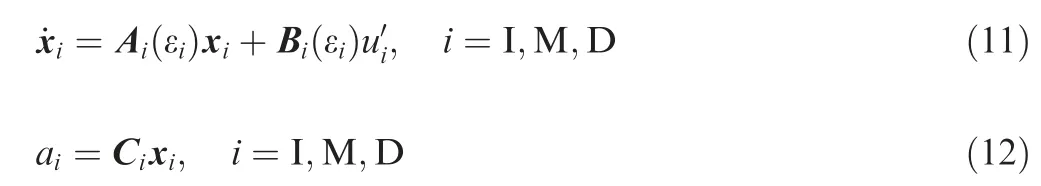
where ui∈[-1,1 ]is the normalized guidance law calculated by

By linearizing the flight around the initial line of sight near the collision triangle, the state vector of the linearized engagement is

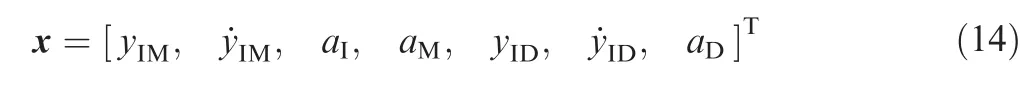
and the equations of motion corresponding to Eq. (14) are given by

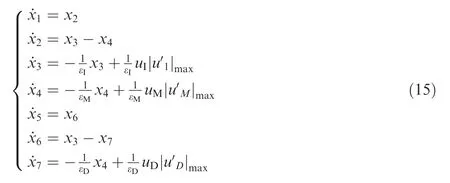
Accordingly, the set of equations of motion is able to be written as

where

2.5. Timeline

According to the linearization assumption,the relative velocity between the interceptor and the maneuvering target can be given as follows corresponding to Eq. (2):The relative velocity between the interceptor and the defender can be given similarly as

Since the initial relative distances between the interceptor and the maneuvering target, and between the interceptor and the defender are rIM0and rID0respectively,where the subscript 0 represents the initial state,the interception time is able to be fixed, and calculated by

We require that the engagement of interceptor and defender terminates before that of interceptor and maneuvering target,thus we have tfID＜tfIM. The nonnegative time-to-go of the interceptor-defender engagement and the interceptor-target engagement can be given respectively by

2.6. Problem statement

In this research, a terminal guidance task of attacking a maneuvering target with active defense for an interceptor is considered. The interceptor with bounded control forces is required to hit the target while evading from the active defender. The guidance problem herein is to design optimal guidance schemes for an interceptor by the use of differential game strategies,such that the position of the interceptor is able to converge to that of the target(yIM→0 as tgo2→0,namely)and maintain certain relative distance with the defender(yID≥η as tgo1→0, namely, where η is a positive constant)in the presence of bounded control effort.

3. Guidance schemes

In this section, guidance schemes for adversaries in the aforementioned engagement scenario are proposed based on differential game strategies. According to the order-reduced model derived by Eq. (16), an optimal guidance law for the interceptor to accomplish the attacking task is proposed by taking into account the control saturation, fuel cost and chattering phenomenon. Satisfaction of the saddle point condition of the guidance law is also analyzed theoretically.

The limit-collision radius η=0.8 m which is double times of the kill radius of KKV and DV. Simulations are done by choosing the weight parameters as ｛α1=8,α2=5,β1=3,β2=5｝.

Simulationresults of Case 1 are presented in Figs. 2-4.Fig. 2 shows the trajectories of the KKV, BM and DV in the scenario and the weight parameters of KKV’s guidance law are chosen as ｛α1=8,α2=5,β1=3,β2=5｝.Fig.3 illustrates the ZEM between the KKV and the BM, and between the KKV and DV, respectively. The acceleration of each player is illustrated by Fig. 4.

The effectiveness of the proposed guidance schemes is validated by simulations of Case 1. Figs. 2 and 3 demonstrates that the KKV could intercept the BM and evade the DV simultaneously. The KKV head towards the BM directly without entrapping the DV until the DV is close enough to threaten the KKV. The ZEM between the KKV and the DV at tgo1=0 is -1.01 m which is larger than the limit-collision radius η, and the ZEM between the KKV and the BM at tgo2=0 is 0.11 m which means the KKV intercept the BM.From Fig. 4 it can be seen that the control force of KKV is not saturated and the chattering phenomenon is also alleviated, which means less fuel cost. However, it also can be seen that the chattering cannot be avoided completely and occurs sometimes. The reason is that the guidance schemes(36) is a type of switching schemes which is non-continuous.By choosing smaller limit-collision radius η can reduce the switching frequency of the guidance laws but may cause safety problem of the KKV. The switching frequency could also be reduced by designing the limit-collision radius η as a function of time-to-go instead of a constant,and the chattering in guidance orders is able to be alleviated further.Case 2. In this case, comparisons of simulation results by different guidance schemes are presented. Two classes of guidance schemes are introduced for comparison in this case.One of them is guidance laws presented in Remark 2 by Eq.(66), which is derived by norm differential game strategy according to Refs.10,17. The other one, which is mentioned in Remark 4 by Eq. (68), is guidance laws proposed by Ref.22based on linear quadratic differential game strategy. Eight numerical examples are presented, and the results are compared to illustrate the control performance.

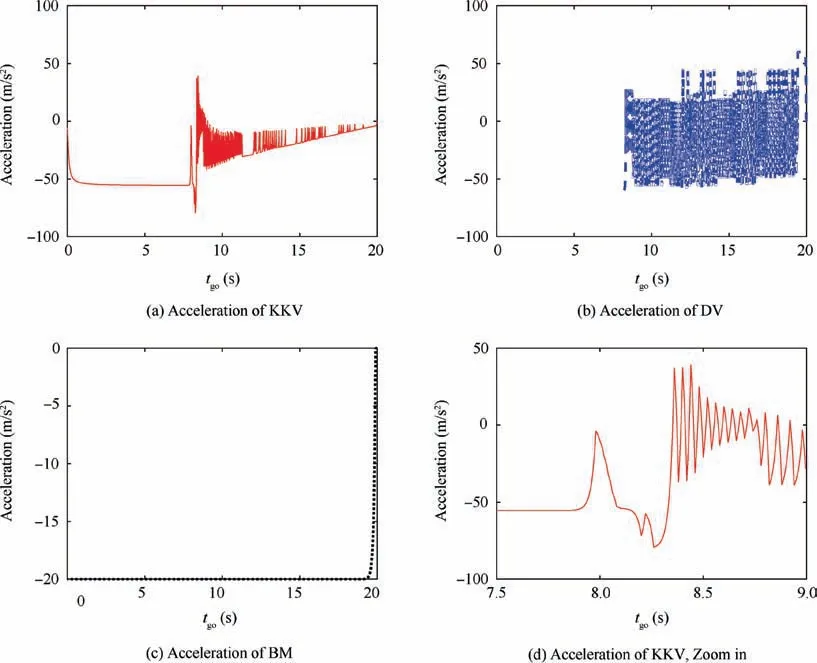
Fig. 4 Accelerations of adversaries by guidance laws (36) （α1 =8,α2 =5,β1 =3,β2 =5）.

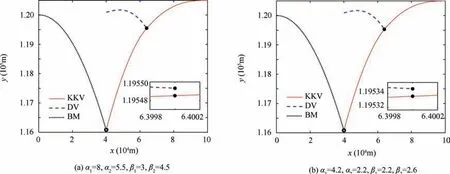
Fig. 5 Trajectories of adversaries by guidance laws (36).

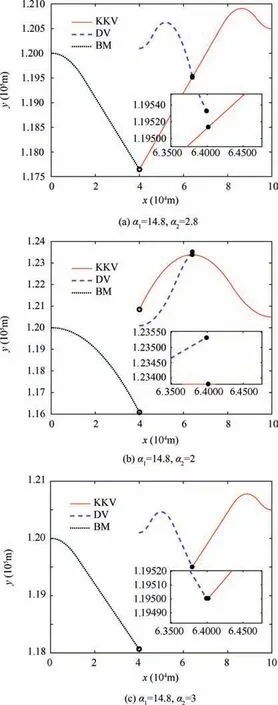
Fig. 6 Trajectories of adversaries by guidance laws (66).

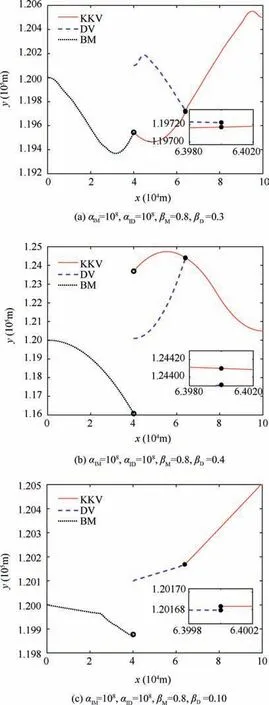
Fig. 7 Trajectories of adversaries by guidance laws (68).

Table 2 Results comparison.

Simulation results of Case 2 are presented in Figs. 5-7.Fig. 5(a) and (b) show the trajectories of the KKV, BM and DV corresponding to guidance laws(36)by varying the weight parameter as ｛α1=8,α2=5.5,β1=3,β2=4.5｝ and｛α1=4.2,α2=2.2,β1=2.2,β2=2.6｝, respectively. Fig. 6(a)-(c) show the trajectories of the KKV, BM and DV corresponding to guidance laws (66) with weight parameters｛α1=14.8,α2=2.8｝, ｛α1=14.8,α2=2｝ and ｛α1=14.8,α2=3｝, respectively. Fig. 7(a)-(c) show the trajectories of the KKV, BM and DV corresponding to guidance laws (68)in Ref.22with weight parameters αIM=108,αID=108,βM=0.8,βD =0.3｝, αIM =108,αID =108,βM=0.8,βD=0.4｝, αIM=108,αID=108,βM=0.8,βD=0.1, respectively.

The results are compared in Table 2.It can be seen that the proposed guidance schemes are able to complete the attack mission without being intercepted by the DV although the weight parameters are changed. The miss distance of interceptor and defender is around 1 m,and the terminal miss distance is around 0.1 m. By choosing weight parameters elaborately,the interceptor could accomplish the attack mission by guidance laws (66) and (68). The terminal miss distance by guidance laws (66) is 0.02 m but with chattering and saturation in control forces.The terminal miss distance by guidance laws(68) is 0.25 m which is larger than that of the proposed guidance laws (36). Furthermore, the guidance laws (66) and (68)are sensitive to the value of weight parameters. By varying the weight parameters α2in Eq. (66) smaller or the weight parameters βDin Eq.(68)larger,the KKV focuses on evading from the DV but ignoring the BM which results in large miss distance of the BM.On the other hand,with larger α2or smaller βD, the KKV concentrates on pursuing the BM but ignoring the DV, which leads to an interception by DV. The presented results verify the tolerance on choosing weight parameters of the proposed guidance schemes. Compared to guidance laws (66) from Ref.17, chattering phenomenon and control saturation is alleviated obviously. Additionally, the terminal miss distance of the proposed guidance schemes is smaller than that of guidance laws (68) in Ref.22.

5. Conclusions

In this research, we solved the optimal guidance problem for an interceptor attacking a ballistic missile with active defense.Based on linear quadratic differential game strategy, a set of optimal guidance schemes for an interceptor in the endgame was proposed by taking into account the fuel cost, control saturation problem and chattering phenomenon. Numerical examples of a scenario consisting of three players were performed. The conclusions are stated as follows:

(1) The guidance schemes in this research were developed based on switching control method and linear quadratic differential game strategy.By virtue of these,the signum function were not used in guidance laws and the weight parameters are easier to choose compared to guidance laws (66) in Ref.17, and the expression and calculation of the proposed guidance schemes are more intuitive and simpler compared to guidance laws (68) in Ref.22.

(2) The effectiveness of the proposed optimal guidance schemes was validated by simulations. The results showed that developed guidance schemes were able to guarantee the convergence of relative distance between interceptor and ballistic missile and the evasion of interceptor from defender.

(3) Compared to other guidance laws developed in the existed references, the results demonstrated that the optimal guidance schemes proposed in this research could reduce the fuel cost of the interceptor, avoid control saturation and alleviate chattering phenomenon,and possess tolerance on choosing weight parameters of the guidance laws.

(4) It should be noted that although the chattering is alleviated but it cannot be avoided completely,since the guidance schemes(36)is a type of switching schemes which is non-continuous. By choosing smaller limit-collision radius η or designing the limit-collision radius η as a function of time-to-go instead of a constant, the switching frequency of the guidance laws should be reduced and the chattering is able to be alleviated further.