基于NMPC的地下无人铲运机反应式导航系统

罗维东，马宝全，孟 宇,2，刘 立，顾 青，白国星，甘 鑫

(1.北京科技大学 机械工程学院，北京 100083; 2.北京科技大学 人工智能研究院，北京 100083)

随着矿产资源的开采深度逐渐加大，地下采矿工作环境变得愈加恶劣。利用矿车自主导航来代替人工驾驶完成地下采矿与运输工作，对于地下采矿工作的安全性和效率性都会有明显的提高[1-3]。铰接式地下矿用车如铲运机(Load-Haul-Dump，LHD)具有良好的驱动能力、通过能力，成为矿产运输的主要设备，开发智能矿用铲运机更是未来的重要发展方向[4-5]。

铲运机的自主导航的工作机制与移动机器人相似，所以在移动机器人的研究基础上，铲运机自主导航依据发展历程可分为两代。其中第1代铲运机自主导航通过追踪地下巷道中类似轨道的导引设施实现自主导航;第2代铲运机自主导航利用信息融合进行定位判定，实现自主导航[6]。第2代自主导航又可分为绝对式导航和相对式导航。绝对式导航需要精确的地图信息，对定位的要求比较高，车辆对预先生成的轨迹进行路径跟踪。相对式导航又称反应式导航，主要通过感知周围环境做出合理的预判，从而做出相应的决策，并不依赖精确的全局地图信息[6-8]。地下采矿巷道狭长且环境恶劣，测绘及铺设基础通讯设备难度较大，定位与建立精确地图耗费人力物力较大，因此无需精确地图信息的反应式导航在地下矿车自主导航中有很大的优势。

反应式导航通常分为环境感知、局部路径决策以及运动控制三大部分。在当前的研究中通常将研究重点放在环境感知系统上[8-10]，但关于局部路径决策和运动控制的具体研究较少，由于反应式导航的决策与控制技术的研究不足，地下无人铲运机在巷道中的跟踪与行驶效果不佳而影响到整体自主导航的工作效果。铲运机的运动控制是多变量多约束的非线性优化问题，因此求解包含复杂多约束的控制问题，对于铲运机的反应式导航的进一步研究有很大帮助。当前有研究人员将滑模控制(Sliding Mode Control，SMC)运用到自主导航的运动控制上，滑模控制鲁棒性较好，但控制器的输出易出现抖振[11-13]。文献[14]阐述了一种“沿墙壁”的地下无人铲运机的反应式导航方法，采用了比例积分微分(Proportional Integral Differentiation，PID)控制，他将巷道视为障碍，使得地下矿车在向前行驶中保证不与巷道壁发生碰撞，能够实现地下无人铲运机的简单路况行驶，但控制算法较为简单，未考虑铲运机的模型和约束条件。由于铲运机存在多约束条件，主流控制算法如PID控制、滑模控制等无法考虑车辆的多约束情况。近年来，模型预测控制算法(Model Predictive Control,MPC)逐渐被运用于地下矿车的自动化，其中Nayl和白国星等将MPC用到了铰接式车辆的自主导航中[15-16]，这些研究表明，MPC可以有效地解决多约束问题，对于约束条件较多的地下铰接式铲运机更加适用。文献[16]将线性时变模型预测控制(Linear Time-varying Model Predictive Control，LTV-MPC)运用到地下无人铲运机的反应式导航上来，其按“角平分线”策略计算当前时刻航线误差，并与PID控制算法的效果进行了对比，证明了MPC算法在转弯时相对于PID控制算法的优越性。LTV-MPC算法虽然采用了预测控制，但其线性化后的预测模型是根据当前误差预测未来误差，在直角转弯等航向变化较大的情况下跟踪误差较大，容易出现转向和回正滞后的情况。文献[16]通过切换航向角和铰接角等控制量解决这一问题，但这种方法对于宽度不定的地下巷道很难自动适应。如在巷道变宽时，运动控制器可能无法及时识别弯道导致转向失败;当巷道变窄时，则容易转向过早难以调整姿态，最终导致碰壁。

本文主要工作如下:① 针对LTV-MPC控制算法在转弯时较差的弯道通过能力和对宽度变化的巷道的适应性，笔者提出了一种基于非线性模型预测控制(Nonlinear Model Predictive Control,NMPC)的运动控制器，通过欧拉法将铲运机运动学模型离散化后推导非线性预测模型，根据当前时刻的状态信息和控制序列预测未来时刻的状态信息，对预测时域内的状态信息与参考路径进行代价计算，求出最优控制序列。由于状态量与控制量采用的是精确的位姿信息而非线性化后的偏差量，在预测算法中不会因丢失实际位姿信息而造成转向过度的情况;② 针对于NMPC控制算法所需要的局部参考路径，提出一种基于巷道环境信息的分段式局部路径决策策略，由于LTV-MPC使用的角平分线策略仅提供当前时刻的航向误差量，通过当前误差量预测未来误差量，但无法提供NMPC所需的参考路径，所以与NMPC控制器并不搭配，故针对NMPC控制器提出基于巷道环境信息的分段式局部路径决策策略，局部参考路径根据铲运机在预测时域内的巷道环境信息动态调整，为NMPC控制器提供参考路径输入信息;③ 通过仿真实验对本文提出的反应式导航系统的效果进行验证，并与基于LTV-MPC的反应式导航系统进行对比，对两者的反应式导航行驶效果进行比较分析。

1 地下无人铲运机反应式导航系统

地下铲运机为铰接式车体，分为前车体与后车体两部分并由刚性铰接体连接，由液压缸驱动车体转向，如图1所示。该结构可以减小转向半径，具有良好的驱动能力、通过能力以及远低于刚性工程车辆的运营成本，在复杂的地下采矿环境机动能力较好，成为了矿产运输的主要装备[11-14]。

图1 地下矿用铰接式铲运机Fig.1 Articulated LHD unit for underground mining

地下无人铲运机的反应式导航系统由环境感知系统、局部路径决策系统和运动控制系统组成，如图2所示，其中，v为前车体速度;ω为铰接角速度。本文的反应式导航系统的环境感知系统由工业激光雷达和射频识别(Radio Frequency Identification，RFID)组成[14-16]，为车辆提供巷道的环境信息。局部路径决策系统根据识别的环境信息和任务目标进行预测时域内局部路径的规划。运动控制器控制铲运机对路径决策系统给出的局部路径进行跟踪，输出实时速度与航向控制量。

图2 反应式导航系统架构Fig.2 Reactive navigation system architecture

在环境感知系统中，激光雷达负责采集巷道的环境信息，同时RFID射频识别系统对关键路口信息进行比对。本文侧重于对局部路径决策系统与运动控制器的改进与设计，以上环境感知系统与文献[14,16]中提出的相同，不再展开介绍。环境感知系统获得的巷道环境信息为局部路径决策策略奠定基础。接下来将对分段式局部路径决策策略进行介绍。

2 分段式局部路径决策策略

对于局部参考路径，文献[16]中的沿“角平分线”策略能够为LTV-MPC控制器提供当前时刻航向偏差量，但NMPC控制器需要铲运机前方一定范围内的巷道参考路径来进行最优控制序列求解，所以“角平分线”策略已不再适用，因此对局部路径决策策略进行重新设计。本文在文献[14]中的“沿墙走”策略基础上，提出一种基于巷道环境信息的分段式局部路径决策策略，并根据实际巷道情况将参考单侧巷道壁改成两侧巷道壁，在直巷道中沿中心线行走，并在弯道行驶中根据地下巷道环境信息进行动态调整，从而确定铲运机需要跟踪的局部参考路径。

反应式导航不需要全局定位与地图信息，所以地下巷道不存在全局坐标系。如图3，4所示，激光雷达P的水平扫描范围为190°，在地下实际巷道中可用激光雷达将巷道壁扫描点滤波、拟合为多段直线，车辆左侧巷道壁拟合直线为l1，车辆右侧巷道壁拟合直线为l2，并且可以得到l1，l2拟合直线相对于车身坐标系的方程，并随车身运动实时改变。如图4,5所示，弯道前设置的RFID射频识别系统可以将弯道信息传递给车辆，其中包括转弯后的左巷道拟合直线l3、右巷道拟合直线l4与转弯前的巷道壁l1,l2的几何关系，为局部参考路径的预测奠定基础。图3～5中，lr为后车体长度;lf为前车体长度;a1为局部参考路径;a2为弯道前的参考路径;a3为弯道后的参考路径;a4为转向结束后的参考路径;b1为巷道宽度;l3为左侧巷道壁拟合直线;l4为右侧巷道壁拟合直线。

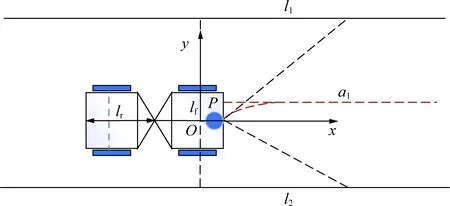
图3 直巷道反应式导航控制策略Fig.3 Reactive navigation control strategy for straight laneway

图4 左转时反应式导航控制策略Fig.4 Reactive navigation control strategy for left turn

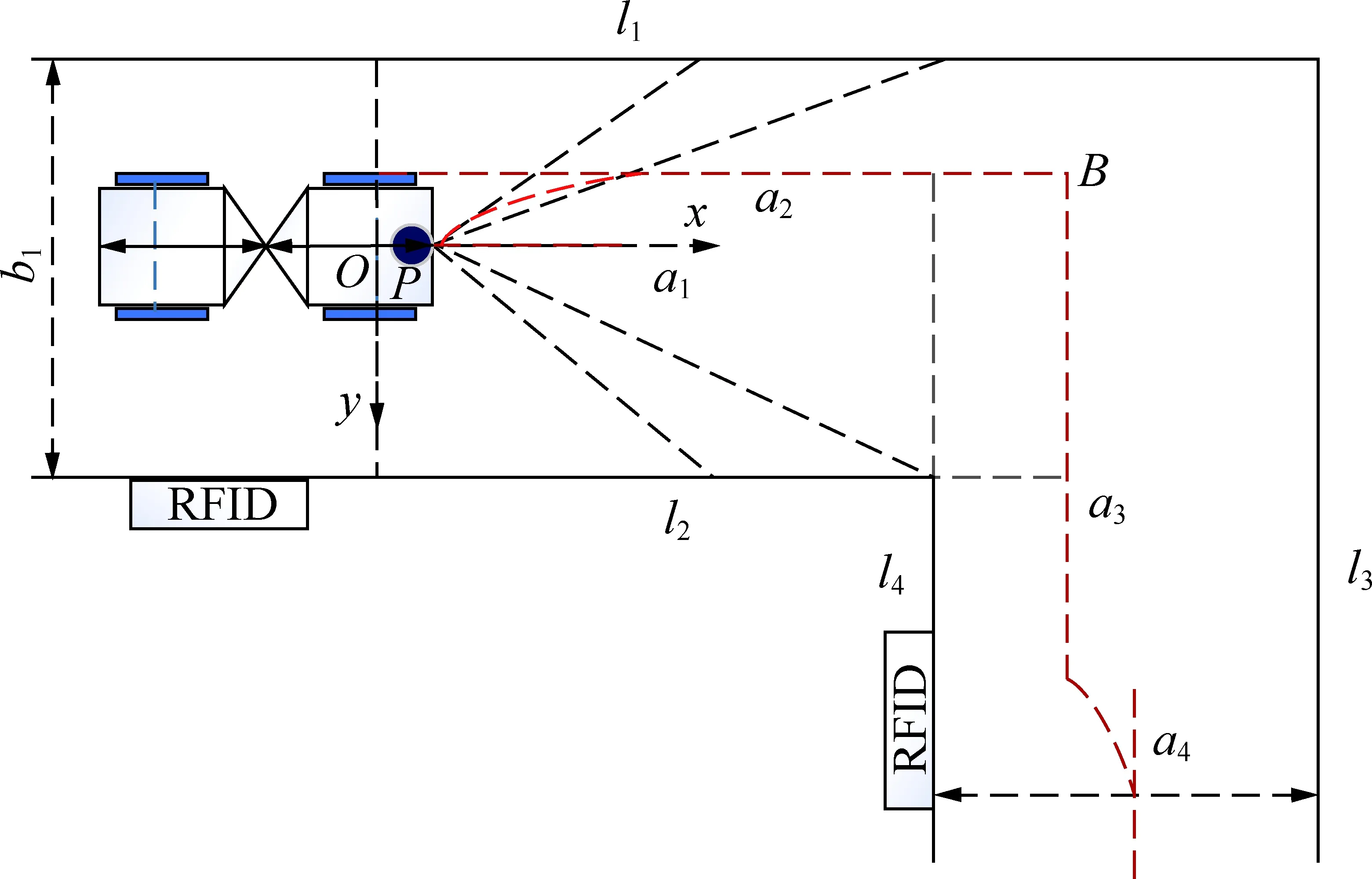
图5 右转时反应式导航控制策略Fig.5 Reactive navigation control strategy for right turn

根据铲运机在地下巷道的行驶路径，可依据激光雷达与RFID系统拟合的基于车身坐标系的巷道壁直线方程将局部路径策略分为4个阶段，其中包括:

(1)直巷道行走阶段。在曲率没有发生较大变化的直线巷道中，如图3，6所示，其中l1，l2两拟合直线平行，可根据左侧巷道壁拟合直线l1，右侧巷道壁拟合直线l2相对于车身坐标系的直线方程来求解巷道中心线a1方程。其中

(1)

式中，k1，k2分别为直线l1，l2的斜率;c1，c2分别为直线l1，l2在车身坐标系y轴上的截距。

图6 车身坐标系上的巷道壁拟合直线Fig.6 Roadway wall fitting line in vehicle Coordinate

已知k1=k2，根据两组拟合直线方程可求出巷道中心线a1基于车身坐标系方程

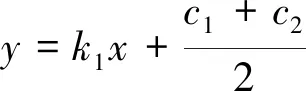
(2)

(2)进入弯道前阶段。在识别到RFID给出的弯道信息即进入弯道前，如图4，5所示，为了提高铲运机转弯时的安全裕度，可将反应式导航策略在“中分线”基础上进行优化，在临近弯道处实行偏离“可能发生碰撞的一侧”的策略，同时考虑到大多地下铲运机宽度小于4 m,将局部参考路径设置为外侧巷道与车身中心的安全距离为2 m的直线a2。根据实际作业情况，可将本阶段分为两种情况，分别为图4所示的左转弯道和图5所示的右转弯道。在左转时，可将参考路径a2设置为远离右侧巷道壁2 m的平行直线以防止转向与内侧巷道刮蹭，如图6所示，局部参考路径a2可根据式(3)得到

(3)

式中，θ1为直线k1的反正切值。

如图5所示，在车辆右转时，可将参考路径设置为远离左侧巷道壁2 m的平行直线a2，同理局部参考路径直线a2方程为

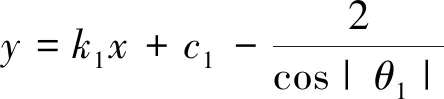
(4)

(3)进入弯道后阶段。由于激光雷达识别能力有限，此时RFID会将转弯后的巷道信息如左侧巷道拟合直线l3、右侧巷道拟合直线l4相对于转弯前巷道直线l1,l2的几何关系进行补充，从而可得到

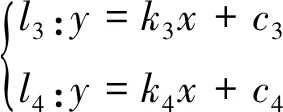
(5)

式中，k3，k4分别为直线l3，l4在车身坐标系的斜率;c3，c4分别为直线l3，l4在车身坐标系y轴上的截距。

若拟合直线l3，l4与车身坐标系x轴垂直，则

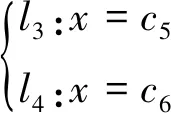
(6)

式中，c5，c6分别为直线l3，l4在车身坐标系x轴上的截距。

如图4，5所示，k3=k4，且l1与l3垂直、l2与l4垂直，即k1k3=-1,k2k4=-1，为防止转弯后与外侧巷道壁刮蹭，可对局部参考路径进行调整，本阶段也分为左转和右转两种情况。左转时，可将转弯后参考路径a3设置为远离左侧巷道壁2 m的平行直线，已知

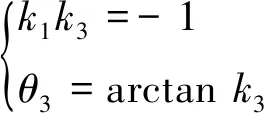
(7)

由于铲运机行走时巷道壁基于车身坐标系的方程是不断变化的，拟合直线相对于车身坐标系的位置不同，如图7所示。因此可根据l3，l4两直线在y轴上的截距大小关系求取参考路径直线a3:

(8)

图7 不同位置时在y轴上的截距关系Fig.7 Intercept relationship on y axis at different positions

若l3，l4与车身坐标系x轴垂直，则参考路径a3为

x=c5+2

(9)

如图5所示，右转时，可将转弯后的参考路径a3设置为远离右侧巷道壁2 m的平行直线，与左转同理可得参考路径a3为

(10)

若l3,l4与车身坐标系x轴垂直，则参考路径a3为

x=c6+2

(11)

在得到参考路径直线a2，a3后，可得到其交点B，如图4，5所示，B点即为参考路径转折点。

(4)转弯完成阶段。如图4，5所示，在完成上述阶段后，到达RFID识别区，根据RFID及激光雷达扫描信息获知转弯完成，再次进入直巷道行走阶段，参考路径为巷道中心线，即

(12)

若l3，l4与车身坐标系x轴垂直，则巷道中心线为

(13)

在第4阶段完成后，铲运机再次进入直巷道阶段，如此循环，以完成反应式导航过程中的局部参考路径规划。得到的参考路径为基于车身坐标系的分段直线，在此基础下可将参考路径直线根据控制器预测步长离散为连续的点，从而得到由点序列组成的局部参考路径。在得到铲运机在巷道的局部参考路径后，其参考信息作为实时输入信息传输到NMPC运动控制器。接下来将对基于NMPC算法的运动控制器设计进行详细介绍。

3 基于NMPC算法的运动控制器设计

笔者以MPC原理为基础，针对LTV-MPC控制器在反应式导航运动控制中存在的局限性，提出了应用于地下无人铲运机反应式导航的NMPC运动控制器[17]。NMPC采用欧拉法将铲运机的运动学模型进行离散化，该预测模型是基于车辆自身状态量与控制量去预测下一时刻的位姿状态量，保留了位姿信息，能够对未来时刻的状态信息与局部参考路径的误差进行代价评测，从而输出每个预测步长的最佳控制量，在复杂巷道能够进行准确地预测与控制[18]。

3.1 非线性预测模型

铰接式铲运机在局部车身坐标系中的运动特征与在全局坐标系中的一致，因此其运动学模型可以参考孟宇、Nayl等建立的铰接车运动学模型[19-20]。在当前铲运机的研究中，通常以前车桥中心Of为车辆控制点。如图8所示，铲运机的前车身和后车身被认为是刚体，轮胎被忽略。表1显示了铰接式车辆模型中各参数的意义。

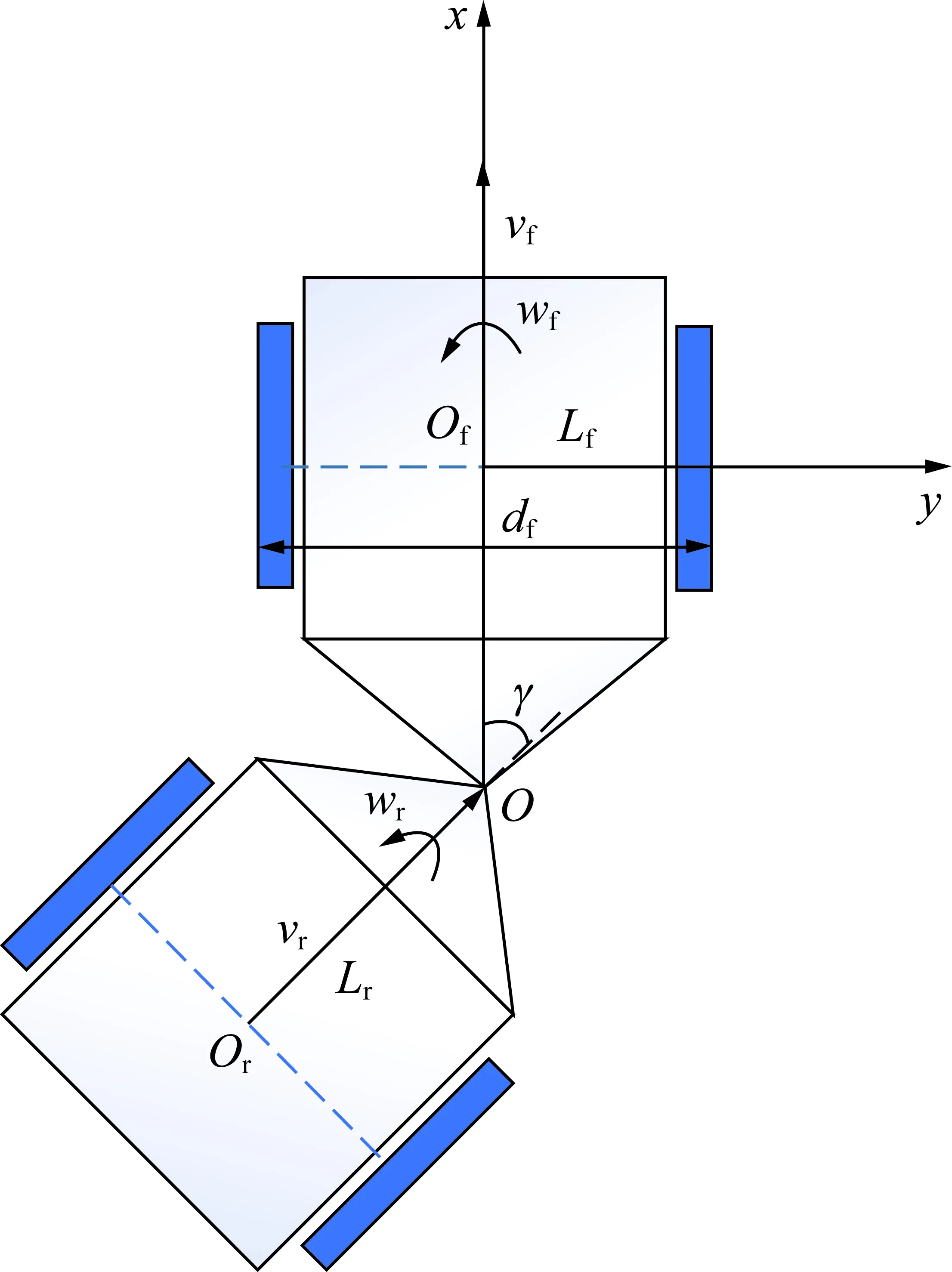
图8 地下无人铰接式铲运机模型Fig.8 Underground unmanned articulated LHD unit model

表1 铲运机各参数物理意义
Table 1 Physical significance of parameters of articulated vehicle

物理意义前车体后车体车桥中心OfOr长度LfLr角速度wfwr速度vfvr宽度dfdr航向θfθr

其中铰接角γ是θf和θr的差:

γ=θf-θr

(14)

根据铲运机的数学关系可以求出

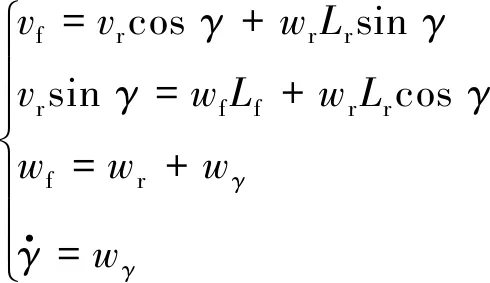
(15)

该铲运机的状态空间模型可由式(15)推导

(16)

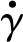
将运动学模型进行离散化，即可得到预测时域内铲运机的位姿状态，将式(16)改为

(17)

由于采样间隔较小，可用欧拉法(Euler Method)将式(17)离散化为

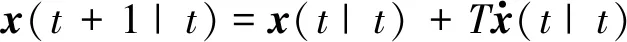
(18)

式中，t为时间;T为采样周期。

同时可得在预测时域Np内未来每一采样时刻机器人的位姿状态:

x(t+Np|t)=x(t+Np-1|t)+

Tf(x(t+Np-1|t),u(t+Nc-1|t))

(19)

其中，Np为预测时域;Nc为控制时域，此时预测层中未来的状态和输出可以由式(19)算出，实现了预测未来状态量的功能。

3.2 控制器优化目标函数设计

在铲运机的预测模型中，系统的未来控制量是未知的，需要通过设定合适的优化目标，求得反应式导航系统下一时刻的最优控制量。

在未来时刻，铲运机的位置与参考轨迹的误差记为e(t):

e(t+Np|t)=x(t+Np|t)-xref(t+Np|t)

(20)

式中，xref为系统局部参考路径信息。

为了使控制量变化平稳，加入控制变量这一约束

Δu(t|t)=u(t|t)-u(t-1|t)

(21)

式中，u(t-1)为上一控制周期的控制量。

因此将优化目标函数设定为

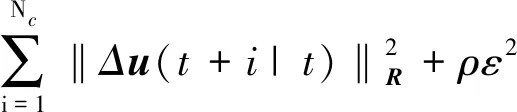
(22)

式中，u为控制变量约束;J为代价函数总值;i=1，2，3,…，N。

在实际控制系统中，往往需要满足状态量及控制量的一些约束条件，如(vfmin,vfmax)，(ωγmin,ωγmax)，(γmin,γmax)。因此需要在每步长内求解以下的带约束的有限时域优化问题:

(23)

s.t.vfmin≤vf(t+i|t)≤vfmax

ωγmin≤ωγ(t+i|t)≤ωγmax

γmin≤γ(t+i|t)≤γmax

其中，Q和R为权重矩阵;ρ为权重系数;ε为松弛因子。第1项反映了系统对参考轨迹的跟踪能力，第2项反映了对控制量平稳变化的要求。

在每个采样时刻内对优化式(23)进行求解，通过优化函数求解得到最优控制序列[21]:

(24)

将第1个控制时域内的控制量作为受控对象的实际控制输入，即

(25)

在下一采样时刻，系统重新以新的采样时刻为初始状态求解优化公式，直至完成整个铲运机反应式导航控制过程。

4 仿真验证

笔者通过MATLAB/Simulink对地下无人铲运机的反应式导航系统进行了仿真验证。地下铲运机的反应式导航不需要全局坐标系，仿真系统采用车身局部坐标系。其中仿真环境为模拟的巷道壁，并设立虚拟激光雷达来识别巷道信息。仿真对照组为文献[16]中的基于LTC-MPC的反应式导航系统，简写为LTV-MPC，本文提出的基于NMPC的反应式导航系统简写为NMPC。

仿真分为两部分：第1部分为直角弯道转向效果的仿真，其中包括两种不同宽度弯道的仿真对比，对两种反应式导航系统在这两种不同宽度的巷道的转向效果进行对比；第2部分为地下无人采矿模拟工作环境的仿真对比，目的是分析铲运机在仿真地下作业巷道的行走效果并对在此环境下的两种反应式导航效果进行分析。为保证对比的严谨性，反应式导航系统及相对应的铲运机模型采用相同的参数，其中，记Θ1为激光雷达的水平扫描角度;s1为激光雷达的水平扫描距离;p为激光雷达的水平分辨率;s2为RFID标签的读写距离;f为RFID标签的工作频率，其余控制参数上文均已提到,见表2。

4.1 不同宽度弯道仿真效果对比

第1组仿真设置了两种不同宽度的仿真巷道。首先，图9(a)为宽度为8 m的直角弯道的两种控制器的对比效果。这组仿真中，NMPC系统与LTV-MPC系统都很好地完成了转弯，但NMPC系统转向较为平滑且离巷道壁最近距离为1.62 m，相对弯道内侧的安全距离较大，同时LTV-MPC系统的最小安全距离也为1.51 m，也达到了很好的控制效果。

表2 仿真系统参数
Table 2 Parameter table of simulation system

控制参数取值Θ1/(°)(-5,185)s1/m(0,80)p/(°)0.25s2/m(0,20)f/MHz(860,960)Lf/m1.80Lr/m1.80Np50Nc1d/m2.80vf/(m·s-1)(1.95,2.05)ωγ/(rad·s-1)(-0.14,0.14)γ/rad(-0.698,0.698)

图9 宽度为8,6 m的直角巷道仿真对比Fig.9 Simulation comparison of 8 and 6 m right-angle laneway

图10依次为两种控制器的速度、铰接角速度、铰接角、航向误差参数的对比，从图10(b)可以看出，LTV-MPC系统由于权重矩阵的设置，使得铲运机达到临界范围时控制量摇摆不定，铰接角速度出现振荡，铲运机执行结构的输出起伏较大，稳定性较差，而由图10(c)，(d)可以看出，两种控制器的铰接角在稳定范围内，同时航向误差均在5 s内收敛到趋近0的稳定状态，其中LTV-MPC为0.003 9 rad，NMPC为0.001 5 rad，总体效果较好。

图10 宽度为8 m的直角巷道车辆参数对比Fig.10 Contrast of vehicle parameters for 8 m right angle laneway

接下来对宽度为6 m的直角巷道的转向效果进行对比，如图9(b)所示，LTV-MPC系统转弯后回正较为迟缓，造成铲运机过度转向，在转向左侧时车辆中心线离巷道壁最小距离为0.52 m，由于车身宽度为2.80 m，此时已造成碰壁，在宽度为6 m的巷道转弯失败;同时NMPC系统能够在该较窄弯道中成功完成转弯，车辆中心线距离巷道壁最小距离为2.13 m，因此车体距离巷道壁最小距离为0.73 m，安全距离提高了1.61 m。

图11 宽度为6 m的直角巷道车辆参数对比Fig.11 Contrast of vehicle parameters for 6 m right angle laneway

图11依次为两种控制器的速度、铰接角速度、铰接角、航向误差参数的对比，图11(b)中依然存在控制器的振荡，并且LTV-MPC系统的铰接角在一段时间内为定值，这是由于该算法采用的线性化后的预测模型为偏差模型，状态量与控制量均为偏差量，在车辆转弯后激光雷达识别为直巷道，铰接角误差量为0，故特别设置权重矩阵进行回正，导致了该算法滞后性较明显，最终偏差为0.68 rad，转向失败。与此对比，NMPC控制器的预测模型为实际状态模型，其铰接角变化较为平顺，响应速度较快，如图11(d)所示，铲运机航向误差在转向后5 s内趋于稳定，最终稳态误差为0.004 2 rad，控制效果较好。

对于以上两种不同宽度巷道，笔者对无人铲运机的主要仿真数据进行了总结，见表3。

4.2 地下作业环境的模拟仿真对比

在第2组仿真中，对地下巷道进行了模拟，铲运机从A区经过两个直角弯道行驶到达C区，如图12所示:第1段A区为6 m×14 m(宽×长)的直巷道，第2段A区到C区的巷道为8 m×36 m(宽×长)的巷道，第3段为6 m×23 m(宽×长)的直巷道。从图13可以看出，两种反应式导航系统都可以很好地完成前两段巷道的自主导航，但LTV-MPC系统在由8 m宽巷道转向C区巷道时未及时转向，出现碰壁情况，而NMPC系统在第3段成功转向，且在转弯时的最小安全距离为1.47 m，比较成功地完成了此工况的自主导航。

表3 直角弯道仿真结果对比
Table 3 Comparison of simulation results of right- angle bend

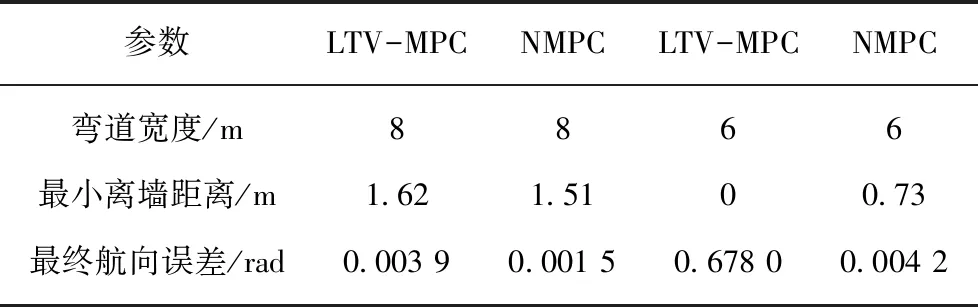
参数LTV-MPCNMPCLTV-MPCNMPC弯道宽度/m8 866最小离墙距离/m1.621.5100.73最终航向误差/rad0.003 90.001 50.678 00.004 2

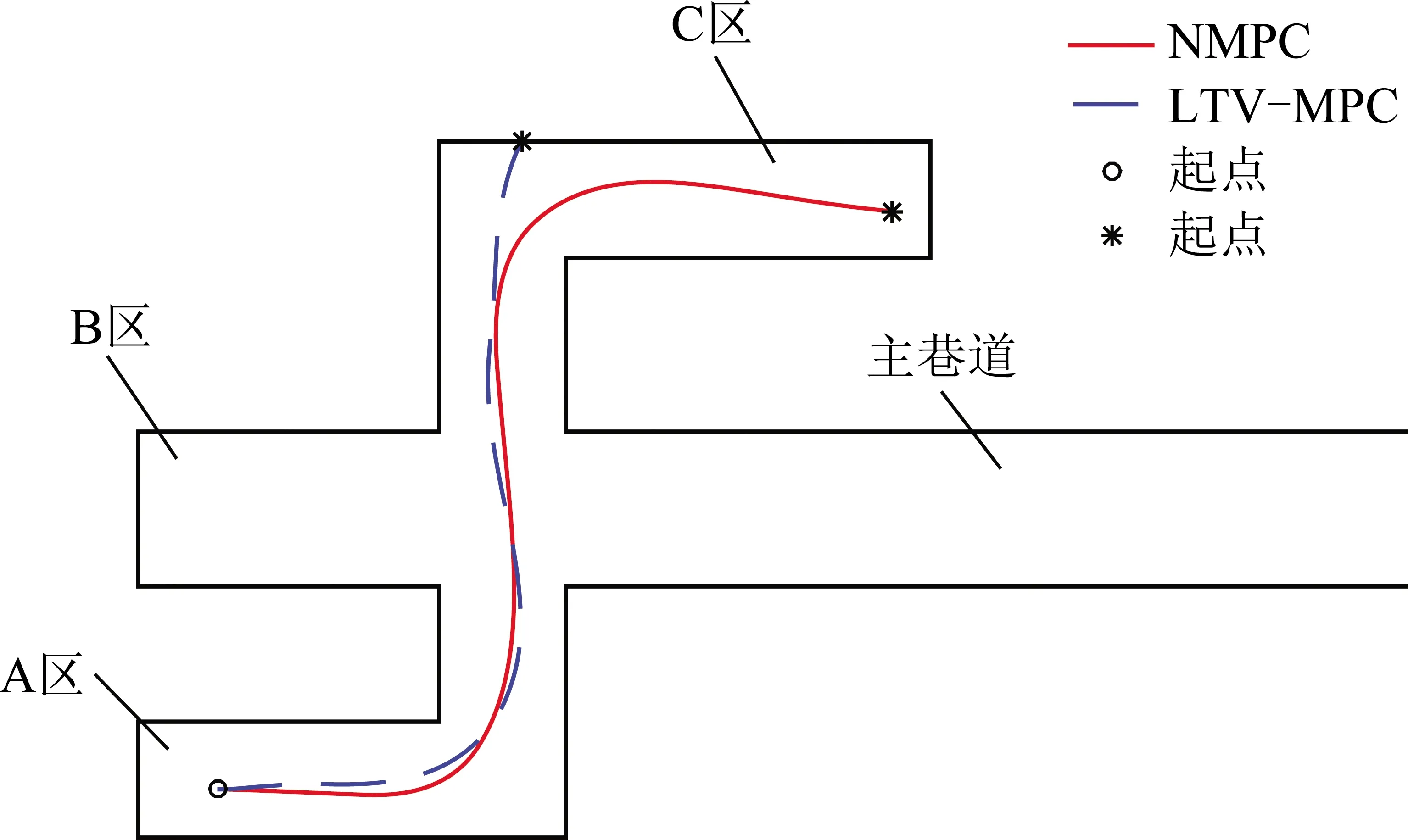
图12 地下巷道工作环境的模拟仿真Fig.12 Simulation of working environment of underground laneway

图13依次为两种控制器的速度、铰接角速度、铰接角、航向误差参数的对比，其反应式导航失败原因与第1组对照组类似，而且从图13(c)控制器的铰接角变化可以看出，LTV-MPC系统的铰接角最大值为0.69 rad，转弯幅度相对NMPC系统较大,难以回正，从图13(b)中可以看出，在第2个弯道LTV-MPC系统的铰接角速度达到了0.14 rad/s，较大的铰接角角速度使得铲运机动作幅度过大，同时造成了1.32 rad的最终航向误差，如图13(d)所示，这也是转弯失败的主要原因。

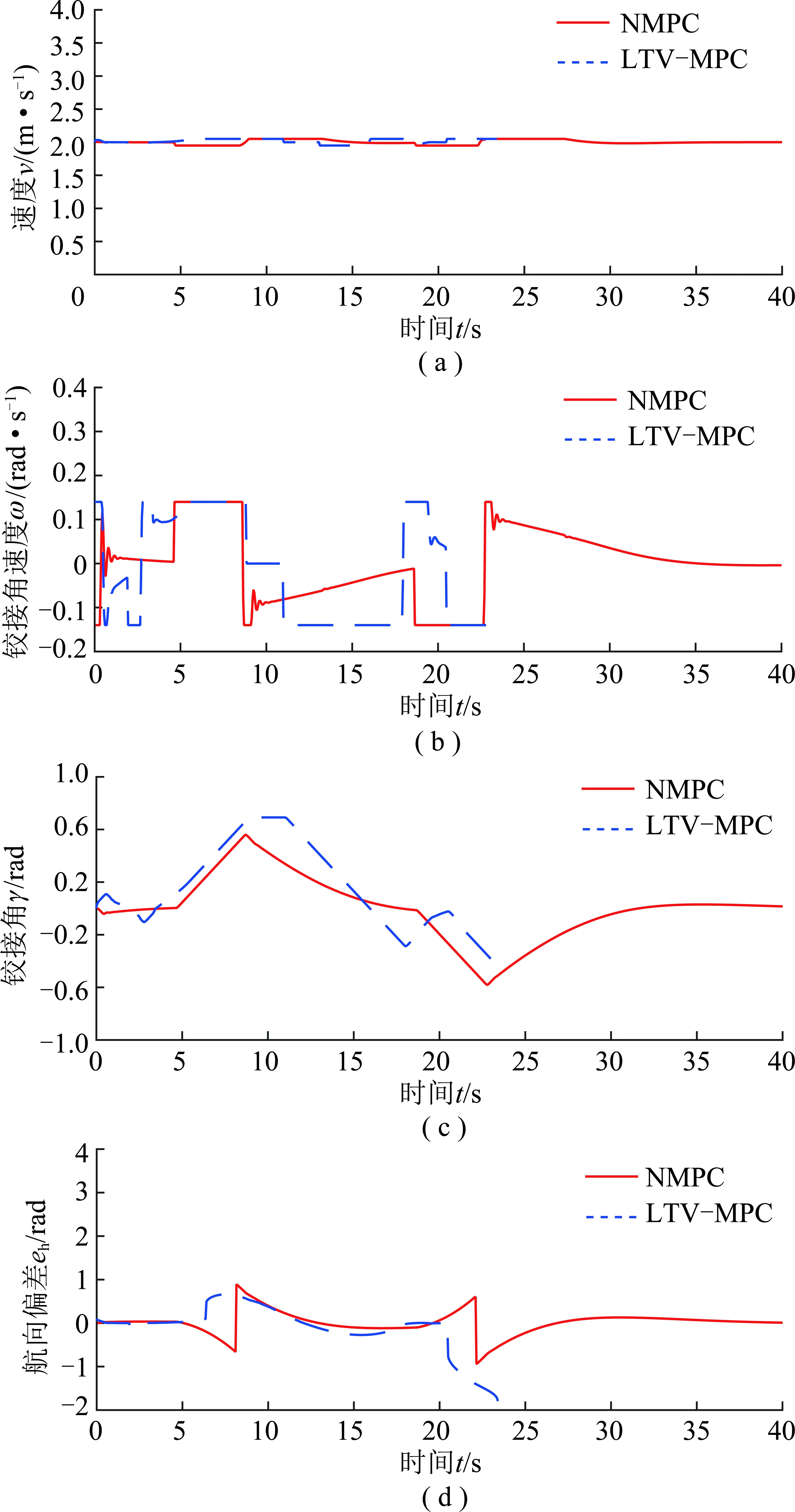
图13 模拟巷道的车辆参数对比Fig.13 Contrast of parameters in simulated laneway

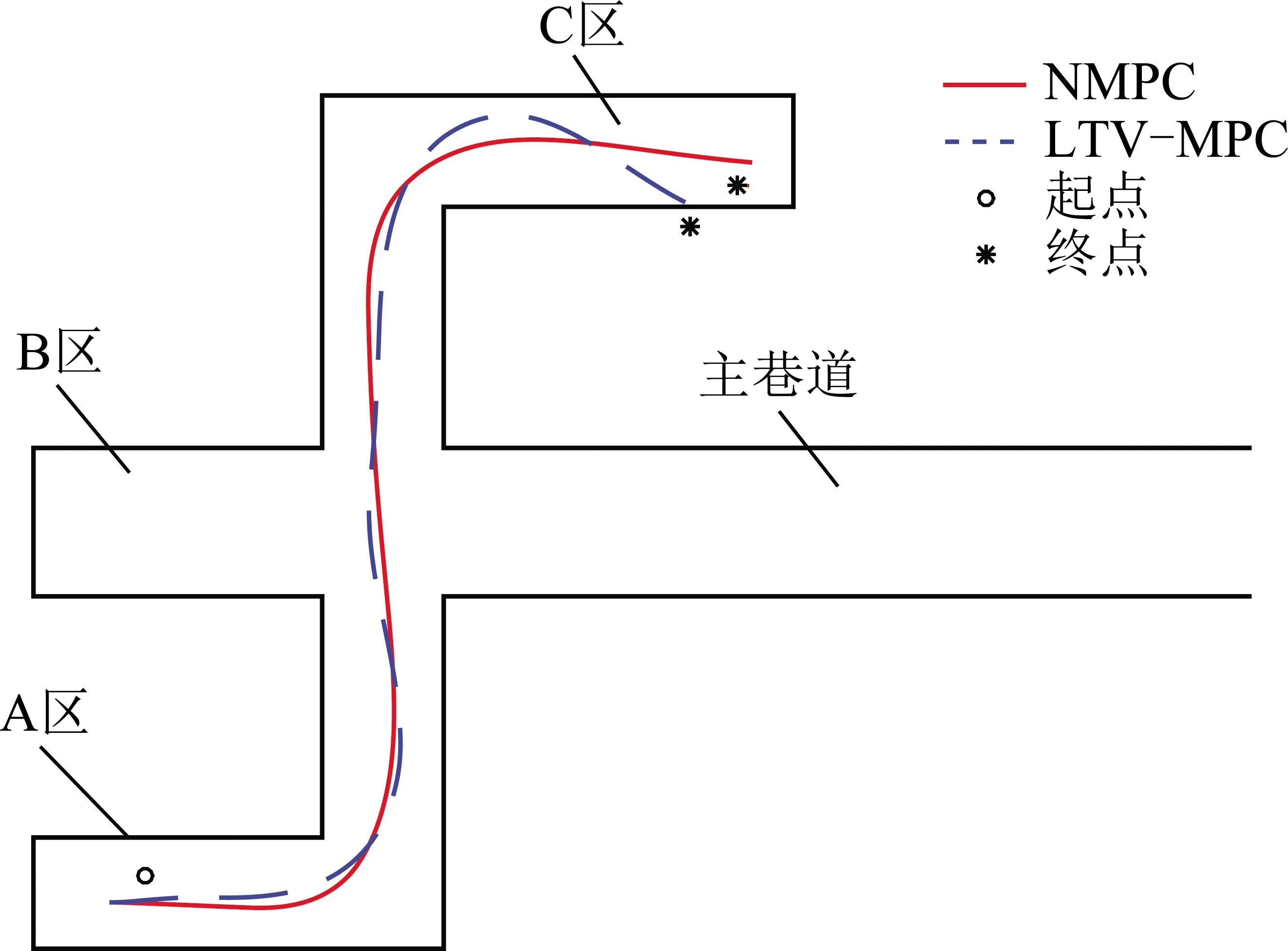
图14 地下长巷道工作环境的模拟仿真Fig.14 Simulation of working environment of long laneway

考虑到仿真铲运机车身较长，LTV-MPC在上述模拟巷道中未能在第2个弯道成功转弯可能由于巷道较短，条件较为苛刻，所以此处将第2段巷道延长，第2段巷道现为8 m×46 m(宽×长)的直巷道。如图14所示，LTV-MPC驱动的铲运机已转入C区，可见LTV-MPC在具有较长的调整时间后效果会变好，但在转入C区后，车身中心离巷道壁最小距离为1.12 m，由于车身宽度为2.80 m，未能及时回正，造成碰壁。同时NMPC系在整个行驶过程离巷道壁最小距离为2.95 m，具有1.55 m的安全距离，安全距离提高了1.83 m。

图15依次为2种控制器对应的车辆的速度、铰接角速度、铰接角、航向误差参数的对比，结合图15(b),(c)来看，LTV-MPC系统的铰接角最大值为0.68 rad，最小值为-0.68 rad，转向幅度较大，难以及时回正。与此对比，NMPC系统能够在5 s内将航向误差由0.89 rad逐渐减小至0，最终误差为0.002 8 rad，反应式导航较为成功。

图15 模拟较长巷道的车辆参数对比Fig.15 Contrast of vehicle parameters in simulated long laneway

同时，在表4中对以上主要仿真结果进行总结，从表4的最终航向误差与最小离墙距离数据的对比也呼应了上述的具体分析结果，验证了NMPC在反应式导航系统中决策与控制的优势。

表4 模拟巷道仿真结果对比
Table 4 Comparison of results in simulated laneway

参数LTV-MPCNMPCLTV-MPCNMPC第2段巷道长度/m36364646最小离墙距离/m01.4701.55最终航向误差/rad1.321 00.001 01.092 00.002 8

5 结 论

(1)本文提出的基于NMPC的反应式导航系统能够较好地解决反应式导航目前存在的转弯性能较差的问题，尤其体现在宽度为6 m的直角巷道的转弯问题和模拟地下工作巷道的工作情况，距离巷道壁最小距离分别为0.73 m和1.47 m，航向偏差能在5 s内最大由0.89 rad收敛至稳定状态，收敛后最小误差分别为0.001 0 rad和0.002 8 rad，较为成功地完成反应式导航任务。

(2)由于使用了经离散化后的非线性预测模型，实际状态信息取代了位姿信息偏差量，对宽度不同的巷道不需要特别切换控制量进行回正，使复杂巷道下控制更为精确，而且避免了输出抖振情况，使得控制器的控制量输出相对平滑，同时铲运机执行机构的工作更为平顺，提高了地下无人铲运机反应式导航的行驶性能。