基于GARCH族模型的中证500指数波动性研究
□ 北京 陶 冶 屈乾龙 李圣行
中证500指数是由全部A股中剔除沪深300指数成份股及总市值排名前300名的股票后,总市值排名靠前的500只股票组成,综合反映中国A股市场中一批中小市值公司的股票价格表现。因此,其也被称为中证小盘指数。上海市场代码为000905,深圳市场代码为399905。现有研究中,对上证指数,深证指数进行研究的较多,直接对中证500指数进行研究的较少,中证500指数受学者的关注程度较低。本文试图对这反映中小市值公司股价的指数做一些初步研究。
一、 相关文献综述
学术界有关金融市场收益率波动性的研究最早开始于上世纪60年代。Mandlebrot(1963)首先提出收益率的波动具有明显的聚集性特征。Engle(1982)提出了ARCH模型及相关衍生模型。Bollerslev(1986)在此基础上,通过ARMA模型建立GARCH模型。Black(1976),Zakoian,J.M.(1994)均使用GARCH模型对股票收益率波动性进行研究,发现股市波动具有非对称效应和杠杆效应的特征,即同等程度的利空消息对股价波动性的影响大于利好消息。Sabiruzza-man 等(2010)对比TGARCH模型和GARCH模型研究香港股票市场指数,发现非对称的TGARCH模型具有更优的拟合效果。
我国学术界关于金融市场收益率波动性的研究相对于国外起步较晚。丁华(1999)通过ARCH(1)以及ARCH(2)模型分析了我国沪市A股指数中的ARCH现象。鲁万波(2006)通过非参数的GRACH(1,1)模型对中国股市进行预测,发现非参数模型更精确。有关中证500指数的研究,杜雨薇(2016)分别采用GARCH模型和EGARCH模型对其指数收益率统计分析,进行趋势预测。
二、 实证分析
1.数据说明。本文的样本为中证500指数交易日的收盘价,样本选取时间为2010年1月4日到2020年4月3日,样本数量为2492,并用 Pt表示中证500指数第 t 天的收盘价,数据来源于Wind数据库。为得到中证500指数的对数收益率,并尽量减少统计误差,本文对中证500的每日收盘价做进行对数差分,即。
2.描述性统计分析。从下图可以看出,中证500指数收益率序列围绕0值上下波动,具有显著的聚集性和时变性特征,且收益率序列与正态分布序列存在明显差异。此外,测得发现其左偏峰度(Kurtosis)6.610797大于3,偏度(Skewness)-0.965625小于0,可知收益率r具有尖峰厚尾的特征,而且左尾较厚,结合其他数据,拒绝正态分布假设。
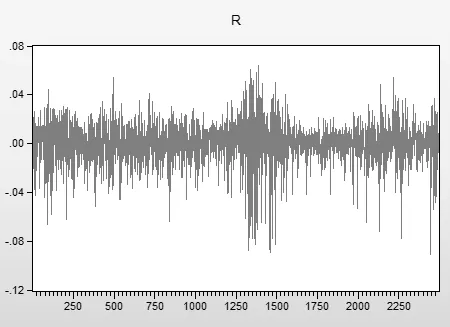
图 中证500指数日收益率r波动图
3.中证500指数收益率序列的平稳性检验。为验证模型的有效性,必须在对时间序列建模前进行平稳性检验。通过检验发现,无论在1%、5%还是10%显著性水平下,ADF单位根检验的统计值均小于相应临界值,t检验统计量值为-46.75124,且P值为0,因此拒绝存在单位根假设,说明中证500指数收益率序列为平稳序列,不存在单位根。
4.不同分布的GARCH族模型的估计结果比较。(1)得出在正态分布、t分布和GED分布下的对中证500指数的收益率序列分别基于GARCH(1,1)、TGARCH(1,1)和EGARCH(1,1)模型的残差估计结果:当正态分布时,三者的对数似然函数值分别为2362.2538、 2365.1685、 2357.6982, AIC值 分 别 为-6.528665、-6.525188、-6.526899;t分布下三者的对数似然函数值分别为2371.6531、2376.9826、2379.5139,AIC值分别为-6.532158、-6.535238、-6.538631;GED分布下三者的对数似然函数值分别为2373.3218、2377.6813、2380.4927,AIC值分别为-6.543965、-6.544288、-6.548647。
对比以上数据,可以发现在三种分布下,非对称的GARCH模型的对数似然函数值都相对于GARCH(1,1)模型更大,对于AIC值则情况正好相反。所以,选择非对称效应下的TGARCH(1,1)模型和EGARCH(1,1)模型对中证500指数收益率的波动进行拟合,准确度更高。(2)如果只看分布状态,根据估计结果,发现三种GARCH模型在t分布和GED分布下的对数似然函数值分别为均大于正态分布下的值。而且t分布和GED分布下的AIC值均小于正态分布下的。这说明,与正态分布相比,通过t分布和GED分布对中证500指数的对数收益率进行拟合,结果更优,同时反映了金融时间序列尖峰厚尾这一重要事实特征。
综上所述,参考AIC信息准则,结合估计结果:本文认为残差服从GED分布的EGARCH(1,1)模型对中证500指数的对数收益率波动拟合效果最佳。
三、结论
对比三种分布下GARCH族模型的估计结果,相较于GARCH(1,1)模型的估计结果,两种非对称GARCH模型的拟合效果均优于前者。因此,选择非对称效应下的TGARCH(1,1)模型和EGARCH(1,1)模型对中证500指数收益率的波动进行拟合,准确度更高。同一模型下,t分布和GED分布下的拟合效果均好于正态分布,由正态性检验,正态分布假设不适用于中证500指数的收益率波动研究。因为存在非对称效应和杠杆效应的存在,中证500指数面临同等程度的利空消息和利好消息时,前者对其所引起的波动高于后者。综上,笔者认为残差服从GED分布的EGARCH(1,1)模型对中证500指数的对数收益率波动拟合效果最佳。
所以,投资者不可人云亦云,盲目操作;中小市值公司经营者应稳定生产,重大消息及时面向市场发布;对于市场监管者来说,应警惕虚假消息对股市的冲击,只有这样,我国股市才能持续健康稳定发展。

