覆盖同余式组及其应用
华 程
(泰州学院 数理学院,江苏 泰州 225300)
0 引言及主要结论
若每个整数都至少满足同余式组
x≡a1(modn1),x≡a2(modn2),…,x≡at(modnt)
(1)
中的1个,这里1 关于覆盖同余式组的性质与构造已有许多结果,具体内容可参考文献[1~4]。 由于覆盖同余式通过一切非负整数,故可用来解决一类与合数有关的数论问题。1980年,著名数学家Erdös曾提出“能否找到一个正整数k,使得k·2n+1对每一个非负整数n均为合数?”的求解问题。文献[5]利用覆盖同余式组证明了k的存在性,并给出21类这样的k值。文献[6]证明了当素数p=7、13及p≡5(mod6)时,存在正整数k,使得2kpn+1对每一个非负整数n均为合数,并猜测当素数p≡1(mod6)时,结论仍成立。文献[7]证明了当素数p=19、31、37、43、61、67、73、79、97时,结论成立。至此提出如下猜想: 猜想 若素数p≡1(mod6),则存在正整数k,使得2kpn+1对每一个非负整数n均为合数。 2017年,文献[7]证明了当素数p≡19、31、37、43、61、67、73、79、97时,猜想成立。 至此,已经证明当素数p≡1(mod6)且7≤p<100时, 猜想成立。 作为该问题的延续, 本文对p≡1(mod6)(100 定理 设素数p=103、109、127、139、151、157、163、181、193、199,则存在正整数k,使得2kpn+1对每一个非负整数n均为合数。 引理1[6]n≡0(mod2),n≡0(mod3),n≡1(mod4),n≡5(mod6),n≡7(mod12)是一组覆盖同余式。 引理2[8](中国剩余定理)设m1,m2,…,mk(k≥2)是两两互素的正整数,令m1m2…mk=M=m1M1=m2M2=…=mkMk,则同余方程组 x≡Ci(modmi),i=1,…,k 有唯一解 这里Miαi≡1(modmi)(i=1,…,k)。 情形1p=103 因为1032≡1(mod3),1033≡1(mod17),1034≡1(mod5),1036≡1(mod7),10312≡1(mod13), 所以 当n≡0(mod2),即n=2m时,有2k·103n+1=2k·1032m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·103n+1=2k·1033m+1≡2k+1(mod17); 当n≡1(mod4),即n=4m+1时,有2k·103n+1=2k·1034m+1+1≡k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·103n+1=2k·1036m+5+1≡ -k+1(mod7); 当n≡7(mod12),即n=12m+7时,有2k·103n+1=2k·10312m+7+1≡ -2k+1(mod13)。 因此,只需k满足下列同余方程组 (2) 由引理1知,对每一个非负整数n,2k·103n+1至少被3、17、5、7、13中一数整除,因而2k·103n+1必是1个合数。 由计算知,(2)式等价于下列同余方程组 (3) 由于模m1=3,m2=17,m3=5,m4=7,m5=13两两互素,故(3)式可用引理2求得k≡2269(mod23205)。于是,所求的正整数k=2269+23205t,这里t是任意非负整数。 情形2p=109 因为1092≡1(mod3),1093≡1(mod7),1094≡1(mod5),1096≡1(mod11),10912≡1(mod13), 所以 当n≡0(mod2),即n=2m时,有2k·109n+1=2k·1092m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·109n+1=2k·1093m+1≡2k+1(mod7); 当n≡1(mod4),即n=4m+1时,有2k·109n+1=2k·1094m+1+1≡ -2k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·109n+1=2k·1096m+5+1≡2k+1(mod11); 当n≡7(mod12),即n=12m+7时,有2k·109n+1=2k·10912m+7+1≡3k+1(mod13)。 因此,只需k满足下列同余方程组 (4) 由引理1知,对每一个非负整数n,2k·109n+1至少被3、7、5、11、13中一数整除,因而2k·109n+1必是1个合数。 由计算知,(4)式等价于下列同余方程组 (5) 由于模m1=3,m2=7,m3=5,m4=11,m5=13两两互素,故(5)式可用引理2求得k≡7843(mod15015)。于是,所求的正整数k=7843+15015t,这里t是任意非负整数。 情形3p=127 因为1272≡1(mod3),1273≡1(mod7),1274≡1(mod5),1276≡1(mod13),12712≡1(mod457), 所以 当n≡0(mod2),即n=2m时,有2k·127n+1=2k·1272m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·127n+1=2k·1273m+1≡2k+1(mod7); 当n≡1(mod4),即n=4m+1时,有2k·127n+1=2k·1274m+1+1≡ -k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·127n+1=2k·1276m+5+1≡ -6k+1(mod13); 当n≡7(mod12),即n=12m+7时,有2k·127n+1=2k·12712m+7+1≡203k+1(mod457)。 因此,只需k满足下列同余方程组 (6) 由引理1知,对每一个非负整数n,2k·127n+1至少被3、7、5、13、457中一数整除,因而2k·127n+1必是1个合数。 由计算知,(6)式等价于下列同余方程组 (7) 由于模m1=3,m2=7,m3=5,m4=13,m5=457两两互素,故(7)式可用引理2求得k≡356926(mod623805)。于是,所求的正整数k=356926+623805t,这里t是任意非负整数。 情形4p=139 因为1392≡1(mod5),1393≡1(mod3),1394≡1(mod7),1396≡1(mod13).13912≡1(mod23), 所以 当n≡0(mod2),即n=2m时,有2k·139n+1=2k·1392m+1≡2k+1(mod5); 当n≡0(mod3),即n=3m时,有2k·139n+1=2k·1393m+1≡2k+1(mod3); 当n≡1(mod4),即n=4m+1时,有2k·139n+1=2k·1394m+1+1≡-2k+1(mod7); 当n≡5(mod6),即n=6m+5时,有2k·139n+1=2k·1396m+5+1≡6k+1(mod13); 当n≡7(mod12),即n=12m+7时,有2k·139n+1=2k·13912m+7+1≡2k+1(mod23)。 因此,只需k满足下列同余方程组 (8) 由引理1知,对每一个非负整数n,2k·139n+1至少被5、3、7、13、23中一数整除,因而2k·139n+1必是1个合数。 由计算知,(8)式等价于下列同余方程组 (9) 由于模m1=5,m2=3,m3=7,m4=13,m5=23两两互素,故(9)式可用引理2求得k≡21907(mod31395)。于是,所求的正整数k=21907+31395t,这里t是任意非负整数。 情形5p=151 因为1512≡1(mod3),1513≡1(mod7),1514≡1(mod13),1516≡1(mod5),15112≡1(mod19), 所以 当n≡0(mod2),即n=2m时,有2k·151n+1=2k·1512m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·151n+1=2k·1513m+1≡2k+1(mod7); 当n≡1(mod4),即n=4m+1时,有2k·151n+1=2k·1514m+1+1≡3k+1(mod13); 当n≡5(mod6),即n=6m+5时,有2k·151n+1=2k·1516m+5+1≡2k+1(mod5); 当n≡7(mod12),即n=12m+7时,有2k·151n+1=2k·15112m+7+1≡ -2k+1(mod19)。 因此,只需k满足下列同余方程组 (10) 由引理1知,对每一个非负整数n,2k·151n+1至少被3、7、13、5、19中一数整除,因而2k·151n+1必是1个合数。 由计算知,(10)式等价于下列同余方程组 (11) 由于模m1=3,m2=7,m3=13,m4=5,m5=19两两互素,故(11)式可用引理2求得k≡3202(mod25935)。于是,所求的正整数k=3202+25935t,这里t是任意非负整数。 情形6p=157 因为1572≡1(mod3),1573≡1(mod13),1574≡1(mod5),1576≡1(mod7),15712≡1(mod17), 所以 当n≡0(mod2),即n=2m时,有2k·157n+1=2k·1572m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·157n+1=2k·1573m+1≡2k+1(mod13); 当n≡1(mod4),即n=4m+1时,有2k·157n+1=2k·1574m+1+1≡-k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·157n+1=2k·1576m+5+1≡3k+1(mod7); 当n≡7(mod12),即n=12m+7时,有2k·157n+1=2k·15712m+7+1≡9k+1(mod17)。 因此,只需k满足下列同余方程组 (12) 由引理1知,对每一个非负整数n,2k·157n+1至少被3、13、5、7、17中一数整除,因而2k·157n+1必是1个合数。 由计算知,(12)式等价于下列同余方程组 (13) 由于模m1=3,m2=13,m3=5,m4=7,m5=17两两互素,故(13)式可用引理2求得k≡20806(mod23205)。于是,所求的正整数k=20806+23205t,这里t是任意非负整数。 情形7p=163 因为1632≡1(mod3),1633≡1(mod7),1634≡1(mod5),1636≡1(mod19),16312≡1(mod13), 所以 当n≡0(mod2),即n=2m时,有2k·163n+1=2k·1632m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·163n+1=2k·1633m+1≡2k+1(mod7); 当n≡1(mod4),即n=4m+1时,有2k·163n+1=2k·1634m+1+1≡k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·163n+1=2k·1636m+5+1≡ -5k+1(mod19); 当n≡7(mod12),即n=12m+7时,有2k·163n+1=2k·16312m+7+1≡ -k+1(mod13)。 因此,只需k满足下列同余方程组 (14) 由引理1知,对每一个非负整数n,2k·163n+1至少被3、7、5、19、13中一数整除,因而2k·163n+1必是1个合数。 由计算知,(14)式等价于下列同余方程组 (15) 由于模m1=3,m2=7,m3=5,m4=19,m5=13两两互素,故(15)式可用引理2求得k≡23089(mod25935)。于是,所求的正整数k=23089+25935t,这里t是任意非负整数。 情形8p=181 因为1812≡1(mod3),1813≡1(mod5),1814≡1(mod7),1816≡1(mod13),18112≡1(mod31), 所以 当n≡0(mod2),即n=2m时,有2k·181n+1=2k·1812m+1≡2k+1(mod3) 当n≡0(mod3),即n=3m时,有2k·181n+1=2k·1813m+1≡2k+1(mod5) 当n≡1(mod4),即n=4m+1时,有2k·181n+1=2k·1814m+1+1≡ -2k+1(mod7) 当n≡5(mod6),即n=6m+5时,有2k·181n+1=2k·1816m+5+1≡ -2k+1(mod13) 当n≡7(mod12),即n=12m+7时,有2k·181n+1=2k·18112m+7+1≡ -10k+1(mod31)。 因此,只需k满足下列同余方程组 (16) 由引理1知,对每一个非负整数n,2k·181n+1至少被3、5、7、13、31中一数整除,因而2k·181n+1必是1个合数。 由计算知,(16)式等价于下列同余方程组 (17) 由于模m1=3,m2=5,m3=7,m4=13,m5=31两两互素,故(17)式可用引理2求得k≡34717(mod42315)。于是,所求的正整数k=34717+42315t,这里t是任意非负整数。 情形9p=193 因为1932≡1(mod3),1933≡1(mod7),1934≡1(mod5),1936≡1(mod97),19312≡1(mod13), 所以 当n≡0(mod2),即n=2m时,有2k·193n+1=2k·1932m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·193n+1=2k·1933m+1≡2k+1(mod7); 当n≡1(mod4),即n=4m+1时,有2k·193n+1=2k·1934m+1+1≡k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·193n+1=2k·1936m+5+1≡ -2k+1(mod97); 当n≡7(mod12),即n=12m+7时,有2k·193n+1=2k·19312m+7+1≡4k+1(mod13)。 因此,只需k满足下列同余方程组 (18) 由引理1知,对每一个非负整数n,2k·193n+1至少被3、7、5、97、13中一数整除,因而2k·193n+1必是1个合数。 由计算知,(18)式等价于下列同余方程组 (19) 由于模m1=3,m2=7,m3=5,m4=97,m5=13两两互素,故(19)式可用引理2求得k≡66979(mod132405)。于是,所求的正整数k=66979+132405t,这里t是任意非负整数。 情形10p=199 因为1992≡1(mod3),1993≡1(mod11),1994≡1(mod5),1996≡1(mod7),19912≡1(mod13), 所以 当n≡0(mod2),即n=2m时,有2k·199n+1=2k·1992m+1≡2k+1(mod3); 当n≡0(mod3),即n=3m时,有2k·199n+1=2k·1993m+1≡2k+1(mod11); 当n≡1(mod4),即n=4m+1时,有2k·199n+1=2k·1994m+1+1≡ -2k+1(mod5); 当n≡5(mod6),即n=6m+5时,有2k·199n+1=2k·1996m+5+1≡3k+1(mod7); 当n≡7(mod12),即n=12m+7时,有2k·199n+1=2k·19912m+7+1≡ -5k+1(mod13)。 因此,只需k满足下列同余方程组 (20) 由引理1知,对每一个非负整数n,2k·199n+1至少被3,11,5,7,13中一数整除,因而2k·199n+1必是1个合数。 由计算知,(20)式等价于下列同余方程组 (21) 由于模m1=3,m2=11,m3=5,m4=7,m5=13两两互素,故(21)式可用引理2求得k≡1633(mod15015)。于是,所求的正整数k=1633+15015t,这里t是任意非负整数。 定理得证。 本文定理进一步支持了文献[6]中提出的猜想,具体给出了使2kpn+1(100 表1 p与q的取值 通过表1发现,当p≡1(mod6)(7≤p<1000)时,猜想都成立。1 引理
2 定理的证明
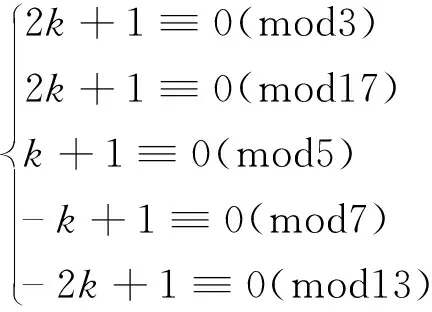

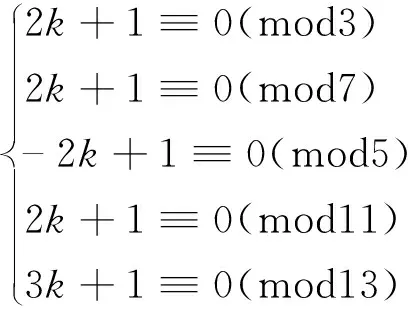


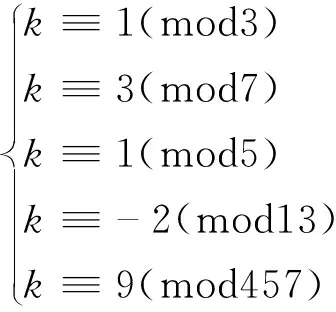
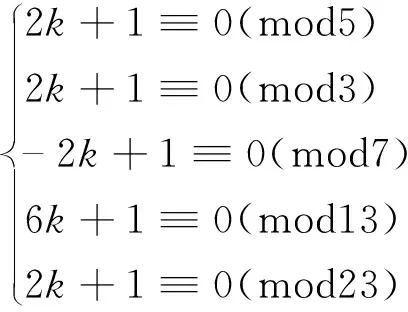






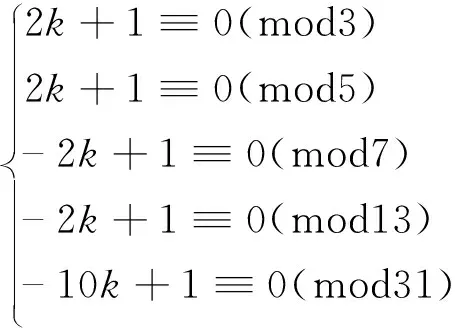

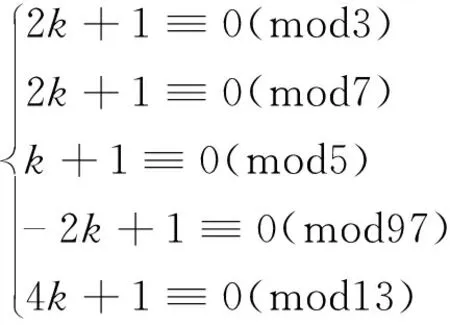

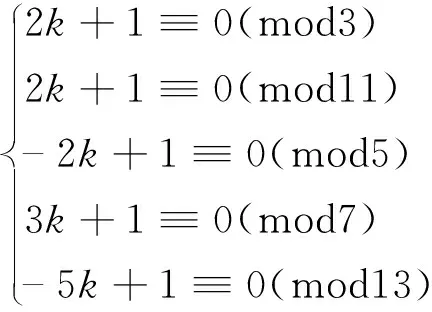

3 结 论


